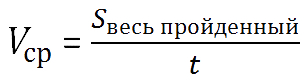Как найти число зная среднее арифметическое
Среднее арифметическое — это число, равное сумме всех чисел множества, делённой на их количество.
Среднее арифметическое двух чисел вычисляется по формуле:
Xср — среднее арифметическое 2-х чисел;
X1 — первое число;
X2 — второе число.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета среднего арифметического двух чисел (среднее между двумя числами). С помощью этого калькулятора вы в один клик сможете рассчитать среднее арифметическое 2-х чисел, если известны исходные числа.
Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.
Смысл коэффициента
Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:
Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.
Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.
Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.
Что такое среднее арифметическое
Средним арифметическим нескольких величин является отношение суммы этих величин к их количеству.
Среднее арифметическое определенного ряда чисел называется сумма всех этих чисел, поделенная на количество слагаемых. Таким образом, среднее арифметическое является средним значением числового ряда.
Чему равно среднее арифметическое нескольких чисел? А равно они сумме этих чисел, которая поделена на количество слагаемых в этой сумме.
Как найти среднее арифметическое число
В вычислении или нахождении среднего арифметического нескольких чисел, нет ничего сложного, достаточно сложить все представленные числа, а полученную сумму разделить на количество слагаемых. Полученный результат и будет средним арифметическим этих чисел.
Рассмотрим этот процесс более подробно. Что же нам нужно сделать для вычисления среднего арифметического и получения конечного результата этого числа.
Во-первых, для его вычисления нужно определить набор чисел или их количество. В этот набор могут входить большие и маленькие числа, и их количество может быть каким угодно.
Во-вторых, все эти числа нужно сложить и получить их сумму. Естественно, если числа несложные и их небольшое количество, то вычисления можно произвести, записав от руки. А если же набор чисел впечатляющий, то лучше воспользоваться калькулятором или электронной таблицей.
И, в-четвертых, полученную от сложения сумму необходимо разделить на количество чисел. В итоге мы получим результат, который и будет средним арифметическим числом этого ряда.
Для чего нужно среднее арифметическое
Среднее арифметическое может пригодиться не только для решения примеров и задач на уроках математики, но для других целей, необходимых в повседневной жизни человека. Такими целями может служить подсчет среднего арифметического для расчета среднего расхода финансов в месяц, или для подсчета времени, которое вы тратите на дорогу, также для того чтобы узнать посещаемость, производительность, скорость движения, урожайность и много другого.
Так, например, давайте попробуем рассчитать, сколько времени вы тратите на дорогу в школу. Идя в школу или возвращаясь, домой вы каждый раз тратите на дорогу разное время, так как когда вы спешите, то вы идете быстрее, и поэтому дорога занимает меньше времени. А вот, возвращаясь, домой вы можете идти не спеша, общаясь с одноклассниками, любуясь природой и поэтому времени на дорогу займет больше.
Поэтому, точно определить время, затраченное на дорогу у вас не получиться, но благодаря среднему арифметическому вы сможете приблизительно узнать время, которое вы тратите на дорогу.
Припустим, что в первый день после выходных, вы потратили на путь от дома до школу пятнадцать минут, на второй день ваш путь занял двадцать минут, в среду вы прошли расстояние за двадцать пять минут, за такое же время составил ваш путь и в четверг, а в пятницу вы никуда не торопились и возвращались целых пол часа.
Давайте найдем среднее арифметическое, прибавив время, за все пять дней. Итак,
15 + 20 + 25 + 25 + 30 = 115
Теперь разделим эту сумму на количество дней
Благодаря такому способу вы узнали, что путь от дома до школы вы приблизительно тратите двадцать три минуты своего времени.
Домашнее задание
1.Путем нехитрых вычислений найдите среднее арифметическое число посещаемости учеников вашего класса за неделю.
2. Найдите среднее арифметическое:
3. Решите задачу:
Тема среднего арифметического и среднего геометрического входит в программу математики 6-7 классов. Так как параграф довольно прост для понимания, его быстро проходят, и к завершению учебного года школьники его забывают. Но знания в базовой статистике нужны для сдачи ЕГЭ, а также для международных экзаменов SAT. Да и для повседневной жизни развитое аналитическое мышление никогда не помешает.
Как вычислить среднее арифметическое и среднее геометрическое чисел
Допустим, имеется ряд чисел: 11, 4, и 3. Средним арифметическим называется сумма всех чисел, поделенная на количество данных чисел. То есть в случае чисел 11, 4, 3, ответ будет 6. Как образом получается 6?
Решение: (11 + 4 + 3) / 3 = 6
В знаменателе должно стоять число, равное количеству чисел, среднее которых нужно найти. Сумма делится на 3, так как слагаемых три.
Теперь надо разобраться со средним геометрическим. Допустим, есть ряд чисел: 4, 2 и 8.
Средним геометрическим чисел называется произведение всех данных чисел, находящееся под корнем со степенью, равной количеству данных чисел.То есть в случае чисел 4, 2 и 8 ответом будет 4. Вот каким образом это получилось:
Решение: ∛(4 × 2 × 
В обоих вариантах получились целые ответы, так как для примера были взяты специальные числа. Так происходит отнюдь не всегда. В большинстве случаев ответ приходится округлять или оставлять под корнем. Например, для чисел 11, 7 и 20 среднее арифметическое ≈ 12,67, а среднее геометрическое — ∛1540. А для чисел 6 и 5 ответы, соответственно, будут 5,5 и √30.
Может ли так произойти, что среднее арифметическое станет равным среднему геометрическому?
Конечно, может. Но только в двух случаях. Если имеется ряд чисел, состоящий только либо из единиц, либо из нулей. Примечательно также то, что ответ не зависит от их количества.
Доказательство с единицами: (1 + 1 + 1) / 3 = 3 / 3 = 1 (среднее арифметическое).
∛(1 × 1 × 1) = ∛1 = 1(среднее геометрическое).
Доказательство с нулями: (0 + 0) / 2=0 (среднее арифметическое).
√(0 × 0) = 0 (среднее геометрическое).
Другого варианта нет и быть не может.
Под понятием среднего арифметического чисел подразумевается результат несложной последовательности расчётов средней величины для ряда чисел, определённых заранее. Необходимо отметить, что такое значение в данное время широко применяется специалистами ряда отраслей. Например, известны формулы при проведении расчётов экономистами или работниками статистической отрасли, где требуется иметь значение данного типа. Кроме этого, этот показатель активно используют и в ряде других отраслей, которые являются смежными с вышеуказанными.
Одной из особенностей расчётов данного значения является простота процедуры. Провести расчёты сможет любой желающий. Для этого не надо иметь специальное образование. Часто нет необходимости применять и вычислительную технику.
В качестве ответа на вопрос как найти среднее арифметическое рассмотрим ряд ситуаций.
Самым простым вариантом расчёта данной величины есть подсчёт её для двух чисел. Процедура проведения расчёта в этом случае является очень простой:
- Первоначально требуется провести операцию сложения выбранных чисел. Это часто можно сделать, как говорится, вручную, не используя электронную технику.
- После того как сложение произведено и получен его результат необходимо произвести деление. Данная операция подразумевает разделение суммы двух сложенных чисел на два – количество сложенных чисел. Именно такое действие и позволит получить требуемую величину.
Формула
Таким образом, формула для подсчёта требуемой величины в случае с двумя будет выглядеть следующим образом:
В этой формуле применяется следующее обозначение:
А и В – это заранее выбранные числа, для которых необходимо находить значение.
Нахождение значения для трёх
Проведение расчёта данной величины в ситуации, когда выбраны три числа, не будет сильно отличаться от предыдущего варианта:
- Для этого следует выбрать числа, необходимые в расчёте, и сложить их для получения общей суммы.
- После того как данная сумма трёх будет найдена, требуется опять совершить процедуру деления. При этом полученную сумму надо разделить уже на три, что соответствует количеству выбранных чисел.
Формула
Тем самым формула, необходимая при проведении расчётов арифметического трёх, будет выглядеть так:
В данной формуле принято следующее обозначение:
А, В и С – это числа, к которым необходимо будет находить среднее арифметическое.
Вычисление среднего арифметического четырёх
Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:
- Выбираются четыре цифры, для которых надо вычислить среднее арифметическое значение. Далее производится суммирование и нахождение конечного результата этой процедуры.
- Теперь чтобы получить окончательный результат, следует взять полученную сумму четырёх и разделить её на четыре. Полученные данные и будут требуемым значением.
Формула
Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:
В данной формуле переменные имеют следующее значение:
А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.
Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.
Подсчёт среднего арифметического пяти
Выполнение данной операции потребует проведения определённого алгоритма действий.
- Прежде всего, надо выбрать пять чисел, для которых будет проходить вычисление среднего арифметического. После данного подбора эти числа, как и в предыдущих вариантах, необходимо просто сложить и получить конечную сумму.
- Полученную сумму надо будет поделить по их количеству на пять, что и позволит получить требуемое значение.
Формула
Тем самым аналогично с ранее рассмотренными вариантами получаем такую формулу для подсчёта среднего арифметического:
В данной формуле переменные имеют такое обозначение:
А, В, С, Е и Р – это числа, для которых необходимо получить среднее арифметическое.
Универсальная формула вычисления
Проводя рассмотрение различных вариантов формул для вычисления среднего арифметического , можно обратить внимание на то, что у них есть общая закономерность.
Поэтому практичнее будет применять общую формулу для нахождения среднего арифметического. Ведь бывают ситуации, когда количество и величина расчётов может быть очень большой. Поэтому разумнее будет использовать универсальную формулу и не выводить каждый раз индивидуальную технологию для расчёта данной величины.
Главным при определении формулы является принцип расчёта среднего арифметическог о.
Данный принцип как было видно из приведённых примеров, выглядит таким образом:
- Производится подсчёт количества чисел, которые заданы для получения требуемого значения. Эта операция может быть проведена как вручную при небольшом количестве чисел, так и при помощи вычислительной техники.
- Проводится суммирование выбранных чисел. Эта операция в большинстве ситуаций выполняется при помощи вычислительной техники, так как числа могут состоять из двух, трёх и более цифр.
- Сумма, которая получена в результате сложения выбранных чисел, должна быть поделена на их количество. Данная величина определяется на первоначальном этапе расчёта среднего арифметического.
Таким образом, общая формула для расчёта среднего арифметического ряда подобранных чисел будет выглядеть следующим образом:
Данная формула содержит следующие переменные:
А и В – это числа, которые выбраны заранее для расчёта их среднего арифметического.
N – это количество чисел, которые были взяты с целью проведения расчёта требуемого значения.
Подставляя каждый раз в данную формулу выбранные числа, мы всегда сможем получить требуемое значение среднего арифметического.
Как видно, нахождение среднего арифметического является несложной процедурой. Однако надо внимательно относиться к проводимым вычислениям и проводить проверку полученного результата. Такой подход объясняется тем, что даже в самых простых ситуациях существует вероятность получения ошибки, которая может повлиять потом на дальнейшие расчёты. В связи с этим рекомендуется применять вычислительную технику, которая способна произвести подсчёты любой сложности.
В математике среднее арифметическое значение чисел (или просто среднее) — это сумма всех чисел в данном наборе, разделенная на их количество. Это наиболее обобщенное и распространенное понятие средней величины. Как вы уже поняли, чтобы найти нужно суммировать все данные вам числа, а полученный результат разделить на количество слагаемых.
Что такое среднее арифметическое?
Давайте рассмотрим пример.
Пример 1 . Даны числа: 6, 7, 11. Нужно найти их среднее значение.
Для начала найдем сумму всех данных чисел.
Теперь разделим получившуюся сумму на количество слагаемых. Так как у нас слагаемых три, соответственно, мы будем делить на три.
Следовательно, среднее значение чисел 6, 7 и 11 — это 8. Почему именно 8? Да потому, что сумма 6, 7 и 11 будет такая же, как трех восьмерок. Это отлично видно на иллюстрации.
Среднее значение чем-то напоминает «выравнивание» ряда чисел. Как видите, кучки карандашей стали одного уровня.
Рассмотрим еще один пример, чтобы закрепить полученные знания.
Пример 2. Даны числа: 3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29. Нужно найти их среднее арифметическое значение.
3 + 7 + 5 + 13 + 20 + 23 + 39 + 23 + 40 + 23 + 14 + 12 + 56 + 23 + 29 = 330
Делим на количество слагаемых (в этом случае — 15).
Следовательно, среднее значение данного ряда чисел равно 22.
Теперь рассмотрим отрицательные числа. Вспомним, как их суммировать. Например, у вас есть два числа 1 и -4. Найдем их сумму.
Зная это, рассмотрим еще один пример.
Пример 3. Найти среднее значение ряда чисел: 3, -7, 5, 13, -2.
Находим сумму чисел.
3 + (-7) + 5 + 13 + (-2) = 12
Так как слагаемых 5, разделим получившуюся сумму на 5.
Следовательно, среднее арифметическое значение чисел 3, -7, 5, 13, -2 равно 2,4.
В наше время технологического прогресса гораздо удобнее использовать для нахождения среднего значения компьютерные программы. Microsoft Office Excel — одна из них. Искать среднее значение в Excel быстро и просто. Тем более, эта программа входит в пакет программ от Microsoft Office. Рассмотрим краткую инструкцию, значение с помощью этой программы.
Для того чтобы посчитать среднее значение ряда чисел, необходимо использовать функцию AVERAGE. Синтаксис для этой функции:
= Average (argument1, argument2, . argument255)
где argument1, argument2, . argument255 — это либо числа, либо ссылки на ячейки (под ячейками подразумеваются диапазоны и массивы).
Чтобы было более понятно, опробуем полученные знания.
- Введите числа 11, 12, 13, 14, 15, 16 в ячейки С1 — С6.
- Выделите ячейку С7, нажав на нее. В этой ячейке у нас будет отображаться среднее значение.
- Щелкните на вкладке «Формулы».
- Выберите More Functions > Statistical для того, чтобы открыть
- Выберите AVERAGE. После этого должно открыться диалоговое окно.
- Выделите и перетащите туда ячейки С1-С6, чтобы задать диапазон в диалоговом окне.
- Подтвердите свои действия клавишей «ОК».
- Если вы все сделали правильно, в ячейке С7 у вас должен появиться ответ — 13,7. При нажатии на ячейку C7 функция (= Average (C1: C6)) будет отображаться в строке формул.
Очень удобно использовать эту функцию для ведения учета, накладных или когда вам просто нужно найти среднее значение из очень длинного ряда чисел. Поэтому ее часто используют в офисах и крупных компаниях. Это позволяет сохранять порядок в записях и дает возможность быстро посчитать что-либо (например, средний доход за месяц). Также с помощью Excel можно найти среднее значение функции.
Ответ: каждому досталось по 4 груши.
Пример 2. На курсы английского языка в понедельник пришло 15 человек, во вторник — 10, в среду — 12, в четверг — 11, в пятницу — 7, в субботу — 14, в воскресенье — 8. Найти среднюю посещаемость курсов за неделю.
Решение: Найдем среднее арифметическое:
| 15 + 10 + 12 + 11 + 7 + 14 + 8 | 77 | 7 | 7 |
Ответ: в среднем на курсы английского языка приходило 11 человек в день.
Пример 3. Гонщик ехала два часа со скоростью 120 км/ч и час со скоростью 90 км/ч. Найдите среднюю скорость автомобиля во время гонки.
Решение: Найдем среднее арифметическое скоростей автомобиля за каждый час пути:
Ответ: средняя скорость автомобиля во время гонки была 110 км/ч.
Пример 4. Среднее арифметическое 3 чисел равно 6, а среднее арифметическое 7 других чисел равно 3. Чему равно среднее арифметическое этих десяти чисел?
Решение: Так как среднее арифметическое 3-х чисел равно 6 то их сумма равна 6 · 3 = 18, аналогично сумма оставшихся 7-ми чисел равна 7 · 3 = 21.
Значит сумма всех 10-ти чисел будет 18 + 21 = 39, а среднее арифметическое равно
Помогите пожалуйста, как найти 3 число если известно среднее арифметическое и первые 2 числа?
Помогите пожалуйста, как найти 3 число если известно среднее арифметическое и первые 2 числа.
Среднее арифметическое чисел — это сумма всех чисел, делённая на их количество — — — — — — — — — — — — — — — — —
1) Среднее арифметическое умножаем на 3 = сумма трёх чисел ;
2) Из суммы трёх чисел вычитаем сумму известных двух чисел = третье число.
Задача?
Первое число на 40% больше второго, а их среднее арифметическое равно 36.
Найти эти числа.
Найти неизвестное число, если число известное равняется 7, 4, а их средне арифметическое — 8, 1?
Найти неизвестное число, если число известное равняется 7, 4, а их средне арифметическое — 8, 1.
Среднее арифметическое двух чисел равно 15?
Среднее арифметическое двух чисел равно 15.
Найди эти числа, если известно, что первое число составляет 50 % от второго числа.
Среднее арифметическое двух чисел равно 6, 4?
Среднее арифметическое двух чисел равно 6, 4.
Известно, что первое число составляет 450% второго числа.
Найдите эти числа.
Как найти среднее арифметическое числа?
Как найти среднее арифметическое числа?
Первое число составляет 70% от второго, а третье число — 50% от второго?
Первое число составляет 70% от второго, а третье число — 50% от второго.
Найти эти числа, если их среднее арифметическое равно 44, 88.
С пасибо, заранее.
Как найти 2 — ое число если известно среднее арифметическое и 1 — ое число?
Как найти 2 — ое число если известно среднее арифметическое и 1 — ое число.
Первое число составляет 70% от второго, а третье число — 50% от второго?
Первое число составляет 70% от второго, а третье число — 50% от второго.
Найти эти числа, если их среднее арифметическое равно 44, 88.
Среднее арифметическое двух чисел равно 6, 4?
Среднее арифметическое двух чисел равно 6, 4.
Известно, что первое число составляет 450% второго числа.
Найдите эти числа.
ПОМОГИТЕ СРОЧНО среднее арифметическое 2х чисел первое число 96 найти второе число?
ПОМОГИТЕ СРОЧНО среднее арифметическое 2х чисел первое число 96 найти второе число.
Вы перешли к вопросу Помогите пожалуйста, как найти 3 число если известно среднее арифметическое и первые 2 числа?. Он относится к категории Математика, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
Как найти числа если известно их среднее арефметическое и что второе на 1,5 больше первого, третье на 1,2 больше первого
Три числа из четырех согласно условиям задачи связаны с величиной четвертого, соответственно, запишем формулу среднего арифметического четырех чисел, введем переменную и решим уравнение.
S4 = (a1 + a2 + a3 + a4)/4;
Пусть x — первое число, (x + 1,5) — второе число, (x + 1,2) — третье число, (x + 1,8) — четвертое число.
Подставим выражения чисел и величину среднего арифметического в формулу:
2,75 = (x + x + 1,5 + x + 1,2 + x + 1,8)/4;
Ответ: Первое число — 1,625, второе — 3,125, третье — 2,825, четвертое — 3,425.
Запомните!
Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму
на их количество.
Пример:
Найти среднее арифметическое 2, 3 и 4.
Обозначим среднее арифметическое буквой «m». По определению выше найдем сумму всех чисел.
2 + 3 + 4 = 9
Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.
В итоге мы получаем формулу среднего арифметического:
Для чего нужно среднее арифметическое?
Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.
Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой
цене вам продавать мячи.
Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены
в магазинах и составим таблицу.
| Магазин | Цена футбольного мяча |
|---|---|
|
«Спорт-товары» |
290 руб. |
| «Adidas» | 360 руб. |
| «Все для футбола» | 310 руб. |
Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?
Если выбрать самую низкую (290 руб.), то мы будем продавать
товар себе в убыток. Если выбрать самую высокую (360 руб.), то покупатели не будут приобретать футбольные мячи у нас.
Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.
Вычислим среднее арифметическое цен на футбольные мячи:
Средняя цена = =
= 320 руб.
Таким образом, мы получили среднюю цену (320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не
слишком дорого.
Средняя скорость движения
Со средним арифметическим тесно связано понятие средней скорости движения.
Наблюдая за движением транспорта в городе, можно заметить, что машины, то
разгоняются и едут с большой скоростью, то замедляются и едут с
маленькой скоростью.
Таких участков на пути следования автотранспорта бывает много. Поэтому
для удобства расчётов, используют понятие средней скорости движения.
Запомните!
Средняя скорость движения — это весь пройденный путь разделить на всё время движения.
Рассмотрим задачу на среднюю скорость.
Разбор примера
Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем
1,5 ч по
грунтовой дороге со скоростью 45 км/ч, наконец
0,3 ч по просёлочной дороге со скоростью 30 км/ч.
Найдите среднюю скорость движения автомобиля на всём пути.
Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем,
и всё время, которое автомобиль двигался.
S1 = V1t1
S1 = 90 · 3,2 = 288 (км)
— шоссе.
S2 = V2t2
S2 = 45 · 1,5 = 67,5 (км)
— грунтовая дорога.
S3 = V3t3
S3 = 30 · 0,3 = 9 (км)
— просёлочная дорога.
S = S1 + S2 + S3
S = 288 + 67,5 + 9 = 364,5 (км)
— весь путь, пройденный автомобилем.
t = t1 + t2 + t3
t = 3,2 + 1,5 + 0,3 = 5 (ч)
— всё время.
Vср = S : t
Vср = 364,5 : 5 = 72,9
(км/ч) — средняя скорость движения автомобиля.
Ответ: Vср = 72,9 (км/ч) — средняя скорость движения автомобиля.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
10 апреля 2015 в 18:52
Дарья Некрасова
Профиль
Благодарили: 0
Сообщений: 3
Дарья Некрасова
Профиль
Благодарили: 0
Сообщений: 3
Автомобиль проехал 180 км за 3 ч с одинаковой скоростью. Из-за гололёда на обратном пути он уменьшил скорость на 15 км/ч. Сколько времени затратил автомобиль на обратный путь.
0
Спасибо
Ответить
10 апреля 2015 в 18:55
Ответ для Дарья Некрасова
Дарья Некрасова
Профиль
Благодарили: 0
Сообщений: 3
Дарья Некрасова
Профиль
Благодарили: 0
Сообщений: 3
180: 3=60
60 ?15=45
180 :45=4
0
Спасибо
Ответить
14 апреля 2015 в 17:11
Ответ для Дарья Некрасова
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
сама себе отвечает?
0
Спасибо
Ответить
Как найти число по его среднему арифметическому?
Вы зашли на страницу вопроса Как найти число по его среднему арифметическому?, который относится к
категории Математика. По уровню сложности вопрос соответствует учебной
программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
Урок
по математике 5 класс (учебник Виленкина)
Среднее
арифметическое
Дидактическая цель урока: познакомить с решением обратных задач, учить находить среднее
арифметическое.
I.
Организационный момент
II.
Устный счет
1. Индивидуальная работа у доски
Задание 1.найдите среднее арифметическое чисел
18,3; 43,5; 32,1 (31,3)
Задание 2.найдите значение выражения
4,777 : 8,5 = 0,562
Задание 3.Решите уравнение
8х – 3,2 = 5,6 (х = 1.1)
2. Фронтальная работа (учащиеся работают вместе с учителем)
(Учитель показывает карточки
с заданием, учащиеся называют ответ, возможно использование слайдов
презентации)
|
2,9 + х = 5,8 |
8,72 : 0,8 |
|
4х – 2,8 = 2 |
7,777 : 7,7 |
|
(6.45 – 5,79) |
7,59 |
3. Взаимопроверка в парах
4. Решите задачу
В киоске продаются три вида шоколадок
и пять сортов мороженого. Сколькими разными способами можно купить шоколадку и
мороженое?
— что это за задача? Докажите.

вариантов мороженого можно выбрать для первой шоколадки? (5)
— Для второй? Третьей?
— Сколько же различных способов выбора
существует? (35 = 15)
III. Определение темы урока
На доске:
3.5; 3.7; 4,2 60; 65; 85 1.8;
2,5; 6,8
— Какое задание можно придумать для этих
чисел?
(Учащиеся могут предложить разные варианты
заданий для этих чисел, учитель выбирает для выполнения самые интересные,
например найти среднее арифметическоедля этих чисел)
— Что такое среднее арифметическое?
— Сформулируйте тему урока.
IV. Работа по теме урока
1.
Найти среднее арифметическое
чисел
(3,5 + 3,7 + 4,2) : 3 = 3,8
(60 + 65 + 85) : 3 = 70
(1,8 + 2,5 + 6,8) : 3 = 3,7
— Расскажите, как найти среднее
арифметическое нескольких чисел.
2. Найти среднее арифметическое чисел (работа
в парах)
25,6; 28,7; 14,4; 12,8
2,8; 42,3; 7,4; 16,5
32,7; 14,84; 15,3; 21,6
Проверка (взаимопроверка, работа в парах)
(25,6 + 28,7 + 14,4 + 12,8) : 4 = 20,375
(2,8 + 42,3 + 7,4 + 16,5) : 4 = 17,25
(32,7 + 14,84 + 15,3 + 21,6) : 4 = 21,1
3. С.227, № 1498
— Подумайте, что следует из равенства отрезков
АВ и ВС. (Координата точки В является средним арифметическим
координат двух других точек)
— Чему равна координата точки С ? (10,
1)
4. Ответьте на вопросы.
— Как вычислить среднее арифметическое? (Среднее
арифметическое = сумма слагаемых : количество слагаемых)
— Как найти сумму чисел? (сумма слагаемых =
Среднее арифметическое количество слагаемых)
— Как найти количество слагаемых ? (количество
слагаемых = сумма слагаемых : среднее арифметическое)
— Как можно назвать эти задачи по отношению
друг к другу? (Обратные)
V. Решение задач
1. с.228, № 1505
— Какая это задача?
— Можем ли мы найти сумму этих двух чисел,
если известно среднее арифметическое?
— Как это сделать?
— Теперь можем ответить на вопрос задачи?
— Решите задачу.
1) 3,1 2 = 6,2 – сумма двух чисел
2) 6,2 – 3,8 =2,4 – второе число
— Подумайте, можно ли решить эту задачу
алгебраически?
— Что следует обозначить через х?
Тогда среднее арифметическое этих чисел будет
(х + 3,8) : 2.
А по условию среднее арифметическое равно 3,1
Значит можем составить уравнение:
(х + 3,8) : 2 = 3,1
х + 3,8 = 3,1 2
х + 3,8 = 6,2
х = 6.2 – 3,8
х = 2,4 — второе
число.
— Какое решение вам понравилось больше?
2. с.228,№ 1509
— Какой путь решения выберем? (Алгебраический)
— Что обозначим через х?
Пусть меньшее число будет х.
Тогда второе число будет 1,5 х.
Среднее арифметическое этих чисел (х +
1,5 х) : 2
А по условию среднее арифметическое равно 30.
Значит, можем состамить уравнение
(х + 1,5 х) : 2 = 30
2,5х = 30 2
2,5х = 60
х = 60 : 2,5
х = 24 – меньшее
из чисел
24 1,5 = 36 – второе число
VI. Повторение изученного материала
(работа в паре)
С.288, № 1517 (а, б)
3,5х – 2.3х + 3,8 =
4.28 4,7у – (2,5у + 12,4) = 1,9
Ответ:
0,4 Ответ: 6,5
VII. Самостоятельная работа
С.228,№ 1511
|
40 : 0,4 = 100 |
100 : 0,1 = 1000 |
0,18 : 0,6 = 0,3 |
|
0,8 : 0,2 = 4 |
1000 : 0,01 = 100 000 |
0,1 : 0,01 = 10 |
|
20 : 0,5 = 40 |
6 : 0,3 = 20 |
1 : 0,5 = 2 |
VIII. Рефлексия
— Как найти сумму чисел, если известны среднее
арифметическое и количество слагаемых?
— Как вы оцениваете себя на этом уроке?
— А как вы оцениваете своего товарища,
который работал с вами в паре?
Домашнее задание
С.230, № 1528, 1532, 1534 (б).
Среднее арифметическое
Среднее арифметическое – это частное от деления суммы чисел на их количество.
Пример 1. Найти среднее арифметическое двух чисел: 4 и 6.
Решение: Сначала найдём сумму данных чисел:
Затем разделим полученный результат на количество слагаемых, то есть на 2:
Значит среднее арифметическое двух чисел (4 и 6) равно 5.
Пример 2. Найти среднее арифметическое чисел 15, 8, 20 и 13.
Решение: Сначала найдём сумму данных чисел:
15 + 8 + 20 + 13 = 56.
Затем разделим полученный результат на количество слагаемых:
Из данных примеров можно сделать вывод, что для нахождения среднего арифметического, нужно сложить все числа и поделить их сумму на их количество.
Рассмотрим задачи, в которых требуется найти средне арифметическое нескольких чисел, относящихся к одной величине.
Задача 1. Утром температура была 15 градусов, днём она поднялась до 27 градусов, а вечером опустилась до 19, ночью температура достигла отметки в 11 градусов. Найти среднюю температуру за сутки.
Решение: Сначала найдём общую сумму температур за сутки:
15 + 27 + 19 + 11 = 72,
затем разделим полученную сумму на 4:
Ответ: средняя температура за сутки равна 18 градусам.
Задача 2. В магазине продали 6 килограммов яблок по цене 55 рублей за килограмм и 4 килограмма груш по цене 75 рублей за килограмм. Какая средняя цена 1 килограмма фруктов?
Решение: Сначала посчитаем сколько всего денег получил магазин за фрукты:
55 · 6 = 330 (р) — выручка за яблоки;
75 · 4 = 300 (р) — выручка за груши;
330 + 300 = 630 (р) — общая выручка за фрукты.
Затем найдём общий вес фруктов:
теперь разделим общую выручку на общий вес проданных фруктов и получим среднюю цену за 1 кг:
Ответ: средняя цена 1 килограмма проданных фруктов — 63 рубля.
Простая формула, чтобы подсчитать среднее арифметическое
О чем эта статья:
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Как найти среднее арифметическое
Как найти среднее арифметическое чисел? Повторим правило и рассмотрим его применение на конкретных примерах.
Чтобы найти среднее арифметическое чисел, надо:
1) сложить эти числа;
2) результат разделить на количество слагаемых:
Найти среднее арифметическое чисел:
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат поделить на 2:
2) 12,6, 14,7 и 16,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3:
(12,6 + 14,7 + 16,5):3=14,6.
3) 40,52, 44,63, 52,34 и 58,29.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4:
(40,52 + 44,63 + 52,34 + 58,29):4=48,945.
4) 17,4. 21,6, 25,2, 28,7 и 30,1.
Чтобы найти среднее арифметическое пяти чисел, надо сложить эти числа и результат разделить на 5:
(17,4 + 21,6 + 25,2 + 28,7 + 30,1):5=24,6.
81 Comments
КЛАСС Я ВСЁ ПОНЯЛ!
Все ясно,просто моментально вспомнила
Я понял но это не точно
Я ВООБЩЕ ВСЕ ПОНЯЛА. Д/З НА 10 СДЕЛАЛА. ( ПРИМЕРЫ ЛИШНЕЕ )
Если каждую новую тему постараться разобрать сразу же, не откладывая на «когда-нибудь потом», то оказывается, что математика — не такой уж сложный предмет.
Поля, желаю Вам дальнейших успехов в учебе!
Среднее арифметическое 4 чисел равно 7.6, а среднее арифметическое 10 других чисел равно 3.6. Найдите значение среднего арифметического этих 14 чисел. Помогите решить, пожалуйста.
Как найти среднее арифметическое число 5,24
Данил, Вы имеете в виду среднее арифметическое чисел 5 и 24? Чтобы найти среднее арифметическое 5 и 24, надо сумму этих чисел разделить на количество слагаемых: (5+24):2=29:2=14,5.
Найти среднее арифметическое чисел -3, 0, 9
Количество чисел — три. Чтобы найти среднее арифметическое этих чисел, надо их сложить и сумму разделить на 3: (-3+0+9):3=2.
как найти среднее арифметическое чисел с дробями?
Валерия, так же, как и с другими числами: найти их сумму и разделить на количество слагаемых.
Спасибо за статью!Статья очень помогла!
Непомогло у меня числа
5, 7, 10, 12, 16
Как решить-среднее арифметическое семи чисел равно 10,2,а среднее арифметическое трёх других чисел-6,8.Найдите среднее арифметическое этих десяти чисел.
Валентина, специально в ответ на аналогичный вопрос Вероники написала пост (ссылка вверху, за 27.08.2014)
Спасибо я всё понял
Все довольно понятно, но вся соль в том, что у меня 3 числа — неизвестны. :
Лол, перепутал. Не правильно прочитал Д/З, спасибо за статью!
класс всё понял за дз получил 5. спс !
Отличная новость, Илья! Поздравляю!
Здрасте как найти среднее арифметическое этих чисел 60 75 и 270 ??
Как и любое другое среднее арифметическое чисел: сложить и поделить на их количество. Если у Вас три числа- (60+75+270)6:3. Если два — (6075+270):2.
среднее арифметическое чисел равно 47.первые три числа равны 37 6 81 найдите четвертое число
Супер!! Оказывается все ОЧЕНЬ легко!! Так мало написанно, но понятно!! 🙂
Среднее арифметическое чисел:
x; 3; 2,1; 2,1
равно 2,55
Найти x
А откуда нужно брать знаменатель?
Делим на количество слагаемых. То есть сколько чисел, среднее арифметическое которых надо найти, дано, на то и делим.
Ребят помогите вот что нам сказали сделать: среднее арефметическое 2 чисел=18.1число=350% второго числа.
Пусть x — I число, тогда II — 3,5x (так как составляет 350% от I-го). Так как их среднее арифметическое равно 18, сосавим и решим уравнение: (x+3,5x):2=18; 4,5x=18∙2; x=36:4,5; x=8. Следовательно, I число равно 8, II — 3,5∙8=28.
Дедушке Вите 90 лет. Средний возраст внуков 20. Среднее арифметическое дедушки и его внуков 22 года. Найдите кол-во внуков. Помогите решить
Пусть n — количество внуков у дедушки. Чтобы найти средний возраст внуков, надо сумму лет всех внуков и разделить на количество внуков, то есть на n. Таким образом, (сумма лет всех внуков):n=20, следовательно,
сумма лет всех внуков=20n.
Чтобы найти средний возраст дедушки и внуков, надо сложить сумму лет всех внуков и дедушки и разделить на (n+1): (сумма лет всех внуков + 90):(n+1)=22.
Значит, (20n + 90):(n+1)=22. Остаётся решить уравнение.
20n + 90=22(n+1)
20n-22n=22-90
n=34.
Ответ: 34 внука.
Повезло деду :D) 34 внука иметь)
Среднее арифметическое восьми чисел равно 4,3. После того как
из этого набора убрали некоторое число, среднее арифметическое
нового набора стало 3,7. Найдите это число. ПОМОГИТЕ РЕШИТ))
1) Среднее арифметическое восьми чисел равно частному от деления суммы этих восьми чисел на 8. По условию, среднее арифметическое этих восьми чисел равно 4,3. Значит, сумма восьми чисел равна 4,3∙8=34,4.
2) Среднее арифметическое семи чисел равно частному от деления суммы семи чисел на 7. По условию, среднее арифметическое семи чисел равно 3,7. Значит, сумма семи чисел равна 3,7∙7=25,9.
3) Разность между суммой восьми чисел и суммой семи чисел и есть то число, которое убрали:
34,4-25,9=8,5.
Спасибо большое все легко и понятно)
Очень благодарна вам и вашему сайту)
Удачи вам в дальнейшем)
Спасибо, Полина! И Вам удачи и успехов в учёбе!
средняя арифметическая 9и чисел равно 16и. если один из этих чисел равен 0 тогда сколько будет ср.арифметическая остальных?
Среднее арифметическое 9 чисел (а1+а2+…+а8+0):9=16.Отсюда а1+а2+…+а8+0=16∙9=144.
Значит, среднее арифметическое оставшихся восьми чисел (а1+а2+…+а8):8=144:8=18.
Среднее арифметическое трёх чисел 15. Найти эти числа, если второе число число в 1,4 раза,а третье в 1.2 раза больше первого.
Пусть первое из чисел равно х, тогда второе — 1,4х, а третье — 1,2х. Так как их среднее арифметическое равно 15, составим и решим уравнение:(х+1,4х+1,2х):3=15.
Светлана Ивановна, если я правильно вас поняла то в моём случае:записать формулу среднего арифметического трёх чисел одно из ко орых в 3 раза больше другого и в 2 раза меньше третьего, это записываем так(х+3х+3х×2):3,заранее спасибо за ответ
Елена, всё верно.
Среднее арифметическое двух чисел равно 14 одно из чисел 12,4 как найти другое число
(х+12,4):2=14. Отсюда х=28-12,4=15,6.
Среднее арифметическое двух положительных чисел на 30% меньше большего из этих чисел. На сколько процентов оно больше меньшего из этих чисел? (Ответ запишите числом). Помогите, пожалуйста решить!
Примем большее из данных двух положительных чисел за x, а меньшее — за y. Тогда среднее арифметическое этих чисел равно 0,7x.Имеем:
Отсюда x=y:0,4; x=2,5y. Соответственно, среднее арифметическое 0,7x=0,7∙2,5y=1,75y составляет 175% от меньшего числа y. А значит, среднее арифметическое на 75% больше меньшего из чисел.
Внук еще это не проходил в школе,а попробовал ему понравилось искать числа.Сам нашел ваш сайт,сам решил и еще похвастался ,что умеет. Спасибо !!
Плиз,помогите не могу сообразить.Я считаю показатель с 9 утра до 9 вечера,и с 9 вечера до 9 утра,то есть днём допустим у меня показатель 121руб,а вечером 221,среднее получается 171,но если я беру общий показатель за день,то он 141руб.А как мне из дневного и вечернего показателя высчитать общий?А показатель считается так:Я беру выручку и делю на количество.
Олеся, извините, но я не понимаю, о каком показателе Вы говорите.
Светлана Михайловна доброго времени! Подскажите пожалуйста как определить среднее арифметическое нескольких углов. результат нужен в градусах. Спасибо. Сергей
Наверное, просто найти среднее арифметическое градусных мер и результат округлить до градусов (в 1 градусе 60 минут. Соответственно, до 30 минут округляем с недостатком, от 30 и более — с избытком).
Большое спасибо за ответ.
Здравствуйте, как найти среднее арефметическое в таком примере,с двух сторон не известные числа
Пример: …14,18,25,44,30…
Нужно найти какие цифры нужно вставить по краям
Артём, условие неполное, данных недостаточно.
Здравствуйте помогите найти средеарифметическое двух чисел 1,536 и 1,540
Здравствуйте, не могли бы вы помочь… совсем забыла математику. задача:среднее для серии из 70 значений 30. Какова сумма этих значений?
Среднее арифметическое нескольких чисел равно сумме этих чисел, делённой на количество слагаемых. Следовательно, чтобы найти сумму, надо известное среднее арифметическое умножить на количество слагаемых: 30∙70=2100.
А если в ряду есть отрицательные и положительные числа, как тогда?
Все также. Например, среднее арифметическое -9; -3; 7 и 11 равно (-9+(-3)+7+11):4=1,5.
среднее арифметическое двух чисел 7,2,чему равна сумма
(a1+a2):2=7,2. Отсюда a1+a2=7,2∙2=14,4.
Я чётка всё поняла это так легко
Не решить у меня числа 1,8;5;7.
Дроби никто не отменял: (1+8+5+7):4=5,25 или 5 1/4.
Здравствуйте как найти среднее арифметическое число 24,35 и 17,69
Сложить и разделить на 2:
(24,35+17,69):2=21,02.
Как найти среднее арифметическое чисел 73;74;83 и а равное 11,4
мне не помогло, у меня с иксом
Денис, значит, у Вас среднее арифметическое известно, и нужно найти одно из чисел. Для этого составьте и решите уравнение.
Помогите решить: 85,37; 49; 63,2; 76,43 найти среднее арефметическое
Среднее арифметическое чисел равно сумме этих чисел, делённой на количество слагаемых: (85,37+49+63,2+76,43):4. Осталось вычислить.
если среднее геометрическое число двух чисел равно 16,а среднее арифметическое равно 20, найдите их?
Пусть эти числа x и y. Среднее арифметическое (x+y):2=20, x+y=40.
Среднее геометрическое √(xy)=16, xy=256. Искомые числа — 32 и 8.
http://skysmart.ru/articles/mathematic/kak-najti-srednee-arifmeticheskoe