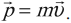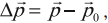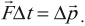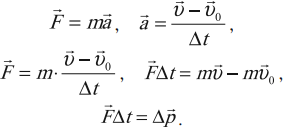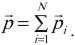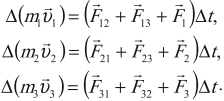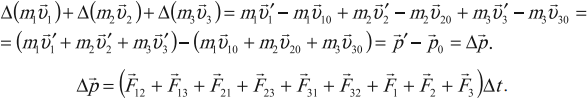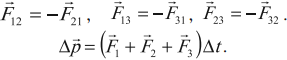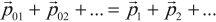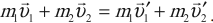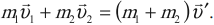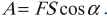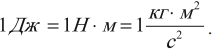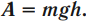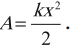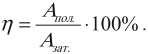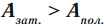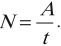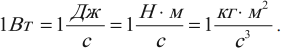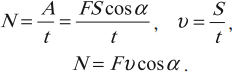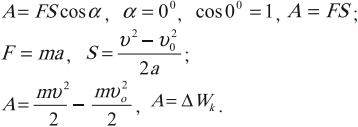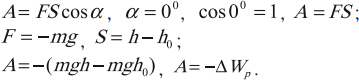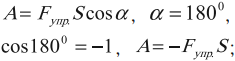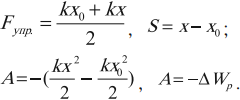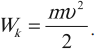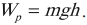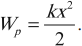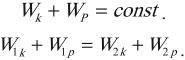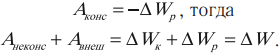Как найти суммарный импульс системы - Avtoru.top

Рассмотрим изменение импульсов тел при их взаимодействии друг с другом.

Если два или несколько тел взаимодействуют только между собой (то есть не подвергаются воздействию внешних сил), то эти тела образуют замкнутую систему.

Импульс, равный векторной сумме импульсов тел, входящих в замкнутую систему, называется суммарным импульсом этой системы.

Результирующая векторная величина импульса системы тел равна векторной сумме импульсов тел, её составляющих:

Закон сохранения импульса
Суммарный импульс системы тел до взаимодействия равен суммарному импульсу этой системы тел после взаимодействия.

В этом заключается закон сохранения импульса, который называют также законом сохранения количества движения.

Закон сохранения импульса впервые был сформулирован Р. Декартом. В одном из своих писем он написал:

«Я принимаю, что во Вселенной, во всей созданной материи есть известное количество движения, которое никогда не увеличивается, не уменьшается, и, таким образом, если одно тело приводит в движение другое, то теряет столько своего движения, сколько его сообщает».

Для примера возьмем систему из двух тел: шары массами

равномерно и прямолинейно движутся со скоростями

, причем их скорости противоположно направлены, то есть шары движутся навстречу друг другу. Импульсы шаров записываются

p1→=m1v1→

p2→=m2v2→

соответственно.

Рис. (1). Направление движения шаров до соударения

Когда шары приблизятся друг к другу, произойдет столкновение. Удар не будет мгновенным, он займёт пусть малое, но вполне измеримое время (t), при этом появятся силы взаимодействия

F1→

F2→

, которые будут приложены к первому и второму шарам соответственно. Как известно, под действием силы скорость тела меняется, поэтому изменятся и скорости шаров. После столкновения модули и направления скоростей могут быть совершенно иными, поэтому обозначим скорости

v1′

v2′

соответственно. Изменятся и импульсы шаров, они станут равны

p1→′=m1v1→′

p2→′=m2v2→′

соответственно.

Рис. (2). Направление движения шаров после соударения

Тогда, согласно закону сохранения импульса, имеют место равенства:

или

m1v1→+m2v2→=m1v1→′+m2v2→′

Данные равенства являются математической записью закона сохранения импульса.

Закон сохранения импульса выполняется и в том случае, если на тела системы действуют внешние силы, векторная сумма которых равна нулю.

Таким образом, более точно закон сохранения импульса формулируется так:

векторная сумма импульсов всех тел замкнутой системы — величина постоянная, если внешние силы, действующие на неё, отсутствуют или же их векторная сумма равна нулю.

Импульс системы тел может измениться только в результате действия на систему внешних сил. И тогда закон сохранения импульса действовать не будет.

Пример:

при стрельбе из пушки возникает отдача: снаряд летит вперёд, а само орудие откатывается назад. Почему?

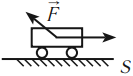
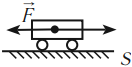
Рис. (3). После выстрела пушка откатывается назад

Снаряд и пушка — замкнутая система, в которой действует закон сохранения импульса. В результате выстрела из пушки импульс самой пушки и импульс снаряда изменятся. Но сумма импульсов пушки и находящегося в ней снаряда до выстрела останется равной сумме импульсов откатывающейся пушки и летящего снаряда после выстрела.

Обрати внимание!

В природе замкнутых систем не существует. Но если время действия внешних сил очень мало, например, во время взрыва, выстрела и т. п., то в этом случае воздействием внешних сил на систему пренебрегают, а саму систему рассматривают как замкнутую.

Кроме того, если на систему действуют внешние силы, но сумма их проекций на одну из координатных осей равна нулю (то есть силы уравновешены в направлении этой оси), то в этом направлении закон сохранения импульса выполняется.

Великий учёный Исаак Ньютон изобрёл наглядную демонстрацию закона сохранения импульса — маятник, или её ещё называют «колыбель». Это устройство представляет собой конструкцию из пяти одинаковых металлических шаров, каждый из которых крепится с помощью двух тросов к каркасу, а тот в свою очередь — к прочному основанию П-образной формы.

Рис. (4). Устройство для демонстрации закона сохранения импульса, колыбель Ньютона

Маятник Ньютона устроен так, что начальный шар передаёт импульс второму шарику, а затем замирает. Нашему глазу на первый взгляд не заметно, как следующий шарик принимает импульс от предыдущего, мы не можем проследить его скорость. Но, если взглянуть пристальнее, можно заметить, как шарик немножко «вздрагивает». Это объясняется тем, что он совершает движения с посланной ему скоростью, но поскольку расстояние очень маленькое, ему некуда разогнаться, то он может на своём коротком пути передать импульс третьему шарику и в итоге остановиться.

Такое же действие совершает и следующий шарик и т. д. Последнему шарику некуда передавать свой импульс, поэтому он свободно колеблется, поднимаясь на определённую высоту, а затем возвращается, и весь процесс передачи импульсов повторяется в обратном порядке.

Самый яркий пример применения закона сохранения импульса — реактивное движение.

Рис. (4). Шаттл

Источники:

Рис. 1. Направление движения шаров до соударения. © ЯКласс.

Рис. 2. Направление движения шаров после соударения. © ЯКласс.

Рис. 3. После выстрела пушка откатывается назад. © ЯКласс. Пушка. Указание автора не требуется, 2021-08-26, Pixabay License, https://pixabay.com/images/id-159503/

Рис. 4. Устройство для демонстрации закона сохранения импульса, колыбель Ньютона.Указание автора не требуется, 2021-08-26, Pixabay License,https://pixabay.com/images/id-6076266/.

Рис. 5. Шаттл. Указание автора не требуется, 2021-08-26, Pixabay License,https://pixabay.com/images/id-992/

Источник

Определение

Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

p = mv

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

10 г = 0,01 кг

Импульс равен:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Определение

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p_1отн2 = m₁v_1отн2 = m₁(v₁ – v₂)

p_1отн2 — импульс первого тела относительно второго, m₁ — масса первого тела, v_1отн2 — скорость первого тела относительно второго, v₁ и v₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

15 т = 15000 кг

p_1отн2 = m₁(v₁ – v₂) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙10³ (кг∙м/с)

Изменение импульса тела

ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:

∆p = p – p₀ = p + (– p₀)

∆p — изменение импульса тела, p — конечный импульс тела, p₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар
	Конечная скорость после удара: v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0.
Абсолютно упругий удар
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p.
Пуля пробила стенку
	Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p₀ – p = m(v₀ – v)
Радиус-вектор тела повернул на 180 градусов
	Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p = 2mv₀
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Определение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

V = a∆t

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Определение

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

положителен, если его направление совпадает с направлением оси ОХ;
отрицателен, если он направлен противоположно направлению оси ОХ.

Важно!

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m₁v₁ = (m₁ + m₂)v
Неупругое столкновение движущихся тел	± m₁v₁ ± m₂v₂ = ±(m₁ + m₂)v
В начальный момент система тел неподвижна	0 = m₁v’₁ – m₂v’₂
До взаимодействия тела двигались с одинаковой скоростью	(m₁ + m₂)v = ± m₁v’₁ ± m₂v’₂

Сохранение проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

m₂v₂ = (m₁+ m₂)v

Отсюда скорость равна:

Задание EF17556

Импульс частицы до столкновения равен −p₁, а после столкновения равен −p₂, причём p₁= p, p₂= 2p, −p₁⊥−p₂. Изменение импульса частицы при столкновении Δ−p равняется по модулю:

а) p

б) p√3

в) 3p

г) p√5

Алгоритм решения

1.Записать исходные данные.

2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.

3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.

4.Подставить известные значения и вычислить.

Решение

Запишем исходные данные:

• Модуль импульса частицы до столкновения равен: p₁= p.

• Модуль импульса частицы после столкновения равен: p₂= 2p.

• Угол между вектором начального и вектором конечного импульса: α = 90^о.

Построим чертеж:

Так как угол α = 90^о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:

Δp=√p21+p22

Подставим известные данные:

Δp=√p2+(2p)2=√5p2=p√5

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17695

На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно

б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено

в) в интервалах 0–1 и 1–2 двигалось равномерно

г) в интервалах 0–1 и 1–2 двигалось равноускорено

Алгоритм решения

1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.

2.Сделать вывод о том, как зависит характер движения от импульса.

3.На основании вывода и анализа графика установить характер движения тела на интервалах.

Решение

Импульс тела есть произведение массы тела на его скорость:

p = mv

Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.

На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.

Верный ответ: б.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22730

Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.

Алгоритм решения

1.Записать исходные данные.

2.Записать закон сохранения импульса применительно к задаче.

3.Записать формулу кинетической энергии тела.

4.Выполнить общее решение.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса камня: m₁ = 3 кг.

• Масса тележки с песком: m₂ = 15 кг.

• Кинетическая энергия тележки с камнем: E_k = 2,25 Дж.

Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:

m1v1+m2v2=(m1+m2)v

Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:

m1v1cosα=(m1+m2)v

Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:

Ek=(m1+m2)v22

Отсюда скорость равна:

v=√2Ekm1+m2

Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:

v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2

Подставим известные данные и произведем вычисления:

v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)

Ответ: 6

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22520

Снаряд, имеющий в точке О траектории импульсp₀, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:

а) −−→AB

б) −−→BC

в) −−→CO

г) −−→OD

Алгоритм решения

1.Сформулировать закон сохранения импульса и записать его в векторной форме.

2.Применить закон сохранения импульса к задаче.

3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.

Решение

Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:

−p1+−p2=−p′
1+−p′2

Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:

−p0=−p1+−p2

Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:

−p2=−p0−−p1

Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18122

Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?

Ответ:

а) 27 г

б) 64 г

в) 81 г

г) 100 г

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.

3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.

4.Выполнить решение задачи в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса пластилиновой пули: m = 9 г.

• Скорость пластилиновой пули: v = 20 м/с.

• Максимальный угол отклонения нити: α = 60°.

Переведем единицы измерения величин в СИ:

Сделаем чертеж:

Нулевой уровень — точка А.

После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:

mv=(m+M)V

После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.

Закон сохранения энергии для точки В:

(m+M)V22=(m+M)gh

V22=gh

Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:

V=√2glcosα

Подставим это выражение в закон сохранения импульса для точки А и получим:

Выразим массу груза:

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 20.2k

Источник

Как определить суммарный импульс?

Чему равен суммарный
импульс двух тел одинаковой массы m, двигавшихся с
одинаковыми по модулю скоростями v во взаимно
перпендикулярных направлениях, после неупругого удара?

Решение.

При абсолютно неупругом
ударе выполняется закон сохранения импульса. После такого удара тела движутся
как одно целое с общей скоростью.

Используя закон сохранения импульса получим,
что суммарный импульс шаров mv₁ + mv₂ = p. Из рисунка найдем по теореме Пифагора модуль суммарного
импульса.

p = mv^2.

Ответ: p = mv^2.

Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.

Источник

Импульсом тела называется произведение его массы на скорость. Также импульс называют количеством движения. Импульс является векторной величиной. Направление его совпадает с направлением скорости.

Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует:

Здесь — изменение импульса за время . Произведение силы на время ее действия называют импульсом силы. Сила здесь может быть и равнодействующей всех сил, действующих на тело.

Закон сохранения импульса – следствие второго и третьего законов Ньютона. Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.

В замкнутой системе суммарный импульс системы тел остается постоянным при любых взаимодействиях тел в системе между собой.

Система тел может быть не замкнута вдоль одной из осей, а вдоль другой – замкнута. Тогда закон сохранения импульса будет работать в такой системе вдоль этой оси. Например, если рассматривать столкновение лодок на озере и не принимать в расчет трение, то такая система может считаться замкнутой вдоль горизонтальной оси, и вдоль этой оси работает закон сохранения импульса. Вдоль вертикальной оси действует сила тяжести, и система не замкнута.

Также при решении задач, связанных с импульсом, очень важны такие понятия, как абсолютно упругий и абсолютно неупругий удары. При абсолютно упругом ударе тело отскакивает от другого тела, сохраняя модуль импульса, и «угол падения равен углу отражения». При абсолютно неупругом ударе тела слипаются, образуя новое тело, масса которого равна сумме их масс. То, что удар был неупругим можно понять, например, если тело отскочило под углом, не равным углу падения, если о неупругом ударе специально не сказано в задаче.

Рассмотрим сначала простые задачи, где движение тел происходит вдоль одной прямой.

Задача 1.

Тело массой кг движется равномерно по окружности, со скоростью м/с. Определить изменение импульса тела после того, как оно пройдет четверть окружности, половину окружности.

Изменение импульса

После того, как тело пройдет четверть окружности, вектор его скорости повернется на 90 градусов, как показано на рисунке — . Изменение скорости можно определить как , поэтому разворачиваем вектор скорости , чтобы получить вектор , и складываем его с по правилу параллелограмма. Зеленым показан вектор изменения скорости . По теореме Пифагора можно найти его длину – он будет равен м/с, тогда изменение импульса тела в этом случае кг*м/с.

Вектора импульсов тел системы

Вектора импульсов и их сложение

Когда тело пройдет половину окружности, вектор его скорости развернется в противоположную сторону — . Точно так же изменение скорости можно определить как , поэтому разворачиваем вектор скорости , чтобы получить вектор , и складываем его с по правилу многоугольника. Зеленым показан вектор изменения скорости . Видно, что м/с.

Изменение импульса тела в этом случае кг*м/с.

Ответ: кг*м/с, кг*м/с.

Задача 2.

Снаряд массой кг вылетает из ствола орудия со скоростью м/с. Зная, что время движения снаряда внутри ствола равно с, определить среднюю силу давления пороховых газов.

На вылете из ствола пушки снаряд обладает импульсом, равным кг*м/с. Так как на систему не действуют никакие внешние силы, то импульс системы сохраняется, а до выстрела он был нулевым. После выстрела суммарный импульс системы также нулевой, а это значит, что импульс снаряда равен по модулю и противоположен по направлению изменению импульса пороховых газов в стволе. Таким образом, газы будут давить с силой кН

Ответ: 1000 кН

Задача 3.

На тело в течение времени с действовала сила Н. Найти массу тела, если изменение скорости тела в результате действия силы равно м/с.

Изменение импульса равно произведению изменения скорости на массу тела. Импульс силы равен , масса тела тогда кг.

Ответ: 100 кг

Задача 4.

Скорость реактивного самолета равна км/ч. На пути самолета оказалась птица массой кг. Определить среднюю силу удара птицы о стекло кабины летчика, если длительность удара с. Каково среднее давление на стекло при ударе, если площадь соприкосновения птицы со стеклом см?

Среднюю силу удара можно определить так:

Скорость самолета выразим в единицах СИ – метрах в секунду. км/ч м/с

Или 500 кН. Можно теперь определить среднее давление на стекло при ударе, только прежде представить площадь в м:

см м

Паскалей или 50 атмосфер.

Ответ: Па или 50 атмосфер.

Задача 5.

Падающий вертикально шарик массой кг ударился о пол и подпрыгнул на высоту 0,4 м. Найти среднюю силу, действующую со стороны пола на шарик, если длительность удара с, к моменту удара о пол скорость шарика м/с.

Шарик двигается равноускоренно, поэтому, когда он соприкоснется с полом, его вес будет больше силы тяжести. А его вес – это, собственно, и есть сила его давления на пол.

При равноускоренном движении вес можно вычислить:

Определим ускорение шарика. Здесь — мера изменения скорости шарика,

Так как шарик взлетел на высоту 0,4 метра, то определим его скорость при отрыве от пола по формуле:

Скорость шарика в наивысшей точке равна 0, поэтому:

Тогда изменение скорости

Ответ: 158 Н

Задача 6.

Шарик летит навстречу стенке со скоростью . Стенка движется навстречу шарику со скоростью . Какой станет скорость шарика после упругого удара о стенку?

Сначала рассмотрим полет шарика относительно стенки. Тогда (если мы представим себе, что смотрим от стенки, и вместе с ней двигаемся со скоростью , не замечая этого) нам будет казаться, что шарик летит на нас со скоростью . Тогда после отскока шарик изменит свою скорость на такую же по модулю, но противоположную по направлению: — это мы его от стенки наблюдаем. А вот теперь мы покинули движущуюся стенку и смотрим с неподвижной земли – и тогда шарик летит уже со скоростью — минус показывает противоположное, относительно первоначального, направление полета.

Задача 7.

Мальчик массой 22 кг, бегущий со скоростью 2,5 м/c, вскакивает сзади на платформу массой 12 кг. Чему равна скорость платформы с мальчиком?

Импульс системы тел будет сохраняться вдоль горизонтальной оси. Поэтому суммарный импульс тележки (0) и мальчика () будет равен суммарному импульсу тележки с мальчиком на ней после прыжка:

Ответ: 1, 62 м/с

Задача 8.

Два неупругих шара с массами 4 и 6 кг движутся со скоростями 8 м/с и 3 м/с соответственно, направленными вдоль одной прямой. С какой скоростью они будут двигаться после абсолютно неупругого удара, если первый догоняет второй? Если они двигаются навстречу?

Запишем закон сохранения в первом случае:

Все слагаемые с плюсами, так как тела движутся в одну сторону.

Теперь тела двигаются навстречу друг другу:

Ответ: 5 м/с, 1,4 м/с

Задача 9.

Тележка с песком катится со скоростью 1 м/с по горизонтальному пути без трения. Навстречу тележке летит шар массой 2 кг с горизонтальной скоростью 7 м/с. Шар после попадания в песок застревает в нем. В какую сторону и с какой скоростью покатится тележка после столкновения с шаром? Масса тележки 10 кг.

Записываем уравнение сохранения импульса системы тел вдоль горизонтальной оси: примем — масса камня, — скорость камня, — масса тележки, — скорость тележки.

За положительное направление примем направление полета камня, тогда скорость тележки будет со знаком «минус»

Получили скорость тележки с камнем со знаком «плюс» — это значит, что она после «поимки» камня поедет в противоположную сторону.

Ответ: 2 м/c

Задача 10.

Средневековая пушка массой 200 кг установлена у края плоской крыши высокой башни. Пушка выпускает ядро массой 5 кг горизонтально, оно приземляется на расстоянии 300 м от стены башни. Пушка, двигаясь без трения, откатывается назад и падает на землю. На каком расстоянии от основания башни она упадет?

Предположим, что высота стены башни . Ядро пушка выпустила горизонтально, и его полет подобен телу, брошенному горизонтально: по горизонтали ядро перемещается с постоянной скоростью, а по вертикали падает, то есть движется равноускоренно.

Тогда ядро будет падать с этой высоты в течение времени, которое можно установить из формулы:

Все это время ядро летит горизонтально с постоянной скоростью, и пролетает 300 метров. Тогда его скорость по горизонтали равна:

Импульс ядра равен импульсу пушки, поэтому пушка откатится назад со скоростью:

Здесь — масса ядра, — его скорость, — масса пушки, — ее скорость.

Найдем горизонтальную скорость пушки:

Пушка падает ровно столько же времени, как и ядро, так как все тела на Земле падают вниз с одним и тем же ускорением, поэтому пушка пролетит за время расстояние от стены до места падения, равное: м

Ответ: 7,5 м

Источник

Законы сохранения в механике

Содержание

Импульс тела
Импульс системы тел
Закон сохранения импульса
Работа силы
Мощность
Работа как мера изменения энергии
Кинетическая энергия
Потенциальная энергия
Закон сохранения механической энергии
Основные формулы по теме «Законы сохранения в механике»

Импульс тела

Импульс тела – это векторная физическая величина, равная произведению массы тела на его скорость:

Обозначение – ( p ), единицы измерения – (кг·м)/с.

Импульс тела – это количественная мера движения тела.
Направление импульса тела всегда совпадает с направлением скорости его движения.
Изменение импульса тела равно разности конечного и начального значений импульса тела:

где ( p_0 ) – начальный импульс тела,
( p ) – конечный импульс тела.

Если на тело действует нескомпенсированная сила, то его импульс изменяется. При этом изменение импульса тела равно импульсу подействовавшей на него силы.

Импульс силы – это количественная мера изменения импульса тела, на которое подействовала эта сила.

Обозначение – ( F!Delta t ), единицы измерения — Н·с.
Импульс силы равен изменению импульса тела:

Направление импульса силы совпадает по направлению с изменением импульса тела.

Второй закон Ньютона (силовая форма):

Важно!
Следует всегда помнить, что совпадают направления векторов:

• силы и ускорения: ( vec{F}uparrowuparrowvec{a} );
• импульса тела и скорости: ( vec{p}uparrowuparrowvec{v} );
• изменения импульса тела и силы: ( Deltavec{p}uparrowuparrowvec{F} );
• изменения импульса тела и ускорения: ( Deltavec{p}uparrowuparrowvec{a} ).

Импульс системы тел

Импульс системы тел равен векторной сумме импульсов тел, составляющих эту систему:

При рассмотрении любой механической задачи мы интересуемся движением определенного числа тел. Совокупность тел, движение которых мы изучаем, называется механической системой или просто системой.

Рассмотрим систему, состоящую из трех тел. На тела системы действуют внешние силы, а между телами действуют внутренние силы.
( F_1,F_2,F_3 ) – внешние силы, действующие на тела;
( F_{12}, F_{23}, F_{31}, F_{13}, F_{21}, F_{32} ) – внутренние силы, действующие между телами.
Вследствие действия сил на тела системы их импульсы изменяются. Если за малый промежуток времени сила заметно не меняется, то для каждого тела системы можно записать изменение импульса в виде уравнения:

В левой части каждого уравнения стоит изменение импульса тела за малое время ( Delta t ).
Обозначим: ( v_0 ) – начальные скорости тел, а ( v^{prime} ) – конечные скорости тел.
Сложим левые и правые части уравнений.

Но силы взаимодействия любой пары тел в сумме дают нуль.

Важно!
Импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.

Закон сохранения импульса

Закон сохранения импульса
Векторная сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой:

Замкнутая система – это система, на которую не действуют внешние силы.
Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций.
При абсолютно упругом ударе взаимодействующие тела до и после взаимодействия движутся отдельно.

Закон сохранения импульса для абсолютно упругого удара:

Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.

Закон сохранения импульса для абсолютно неупругого удара:

Реактивное движение – это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-то его части.
Принцип реактивного движения основан на том, что истекающие из реактивного двигателя газы получают импульс. Такой же по модулю импульс приобретает ракета.
Для осуществления реактивного движения не требуется взаимодействия тела с окружающей средой, поэтому реактивное движение позволяет телу двигаться в безвоздушном пространстве.

Реактивные двигатели
Широкое применение реактивные двигатели в настоящее время получили в связи с освоением космического пространства. Используются они также для метеорологических и военных ракет различного радиуса действия. Кроме того, все современные скоростные самолеты оснащены воздушно-ракетными двигателями.
Реактивные двигатели делятся на два класса:

ракетные;
воздушно-реактивные.

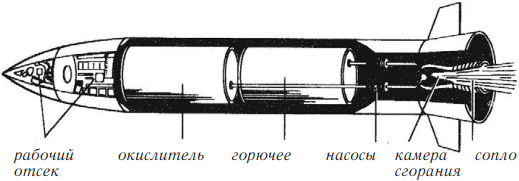
В ракетных двигателях топливо и необходимый для его горения окислитель находятся непосредственно внутри двигателя или в его топливных баках.

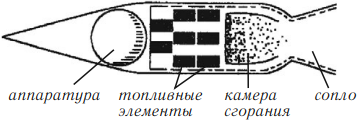
Ракетный двигатель на твердом топливе
При горении топлива образуются газы, имеющие очень высокую температуру и оказывающие давление на стенки камеры. Сила давления на переднюю стенку камеры больше, чем на заднюю, где находится сопло. Выходящие через сопло газы не встречают на своем пути стенку, на которую могли бы оказать давление. В результате появляется сила, толкающая ракету вперед.

Сопло – суженная часть камеры, служит для увеличения скорости истечения продуктов сгорания, что, в свою очередь, повышает реактивную силу. Сужение струи газа вызывает увеличение его скорости, так как при этом через меньшее поперечное сечение в единицу времени должна пройти такая же масса газа, что и при большем поперечном сечении.

Ракетный двигатель на жидком топливе

В ракетных двигателях на жидком топливе в качестве горючего используют керосин, бензин, спирт, жидкий водород и др., а в качестве окислителя – азотную кислоту, жидкий кислород, перекись водорода и пр.
Горючее и окислитель хранятся отдельно в специальных баках и с помощью насосов подаются в камеру сгорания, где температура достигает 3000 0С и давление до 50 атм. В остальном работает так же, как и двигатель на твердом топливе.

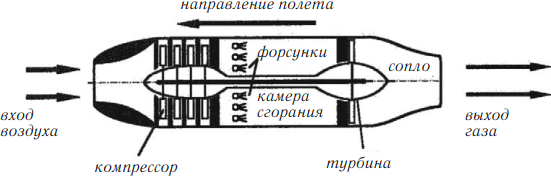
Воздушно-реактивный двигатель

В носовой части находится компрессор, засасывающий и сжижающий воздух, который затем поступает в камеру сгорания. Жидкое горючее (керосин) попадает в камеру сгорания с помощью специальных форсунок. Раскаленные газы выходят через сопло, вращают газовую турбину, приводящую в движение компрессор.
Основное отличие воздушно-реактивных двигателей от ракетных двигателей состоит в том, что окислителем для горения топлива служит кислород воздуха, поступающего внутрь двигателя из атмосферы.

Алгоритм применения закона сохранения импульса к решению задач:

Запишите краткое условие задачи.
Определите характер движения и взаимодействия тел.
Сделайте рисунок, на котором укажите направление векторов скоростей тел до и после взаимодействия.
Выберите инерциальную систему отсчета с удобным для нахождения проекций векторов направлением координатных осей.
Запишите закон сохранения импульса в векторной форме.
Спроецируйте его на выбранные координатные оси (сколько осей, столько и уравнений в системе).
Решите полученную систему уравнений относительно неизвестных величин.
Выполните действия единицами измерения величин.
Запишите ответ.

Работа силы

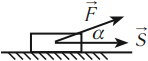
Механическая работа – это скалярная векторная величина, равная произведению модулей вектора силы, действующей на тело, вектора перемещения и косинуса угла между этими векторами.

Обозначение – ( A ), единицы измерения – Дж (Джоуль).

1 Дж – это работа, которую совершает сила в 1 Н на пути в 1 м:

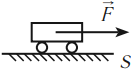
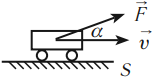
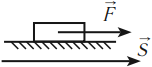
Механическая работа совершается, если под действием некоторой силы, направленной не перпендикулярно, тело перемещается на некоторое расстояние.

Зависимость механической работы от угла ( alpha )

( alpha=0^{circ},, cosalpha=1,, A=FS,,A>0; )

( 0^{circ}<alpha<90^{circ},, A=FScosalpha,,A>0; )

( alpha=90^{circ},, cosalpha=0,, A=0; )

( 90^{circ}<alpha<180^{circ},, A=FScosalpha,,A<0; )

( alpha=180^{circ},, cosalpha=-1,, A=-FS,,A<0; )

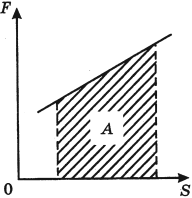
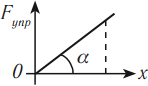
Геометрический смысл механической работы

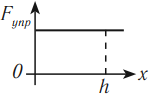
На графике зависимости ( F=F(S) ) работа силы численно равна площади фигуры, ограниченной графиком, осью перемещения и прямыми, параллельными оси силы.

Формулы для вычисления работы различных сил

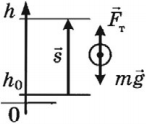
Работа силы тяжести:

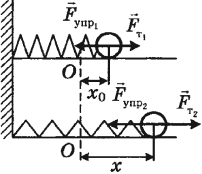
Работа силы упругости:

Коэффициент полезного действия механизма (КПД) — это физическая величина, равная отношению полезной работы, совершенной механизмом, ко всей затраченной при этом работе.
Обозначение – ( eta ), единицы измерения – %.

( A_{mathit{пол.}} ) – полезная работа – это та работа, которую нужно сделать;
( A_{mathit{зат.}} ) – затраченная работа – это та работа, что приходится делать на самом деле.

Важно!
КПД любого механизма не может быть больше 100%.

Мощность

Мощность – это количественная мера быстроты совершения работы.

Обозначение – ( N ), единицы измерения – Вт (Ватт).
Мощность равна отношению работы к времени, за которое она была совершена: .

1 Вт – это мощность, при которой за 1 с совершается работа в 1 Дж:

1 л. с. (лошадиная сила) = 735 Вт.

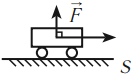
Связь между мощностью и скоростью равномерного движения:

Таким образом, мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов.

Важно!
Если интервал времени стремится к нулю, то выражение представляет собой мгновенную мощность, определяемую через мгновенную скорость.

Работа как мера изменения энергии

Если система тел может совершать работу, то она обладает энергией.

Работа и изменение кинетической энергии (теорема о кинетической энергии)

Если под действием силы тело совершило перемещение и вследствие этого его скорость изменилась, то работа силы равна изменению кинетической энергии.
Силы, работа которых не зависит от формы траектории, называются консервативными.

Работа и изменение потенциальной энергии тела, поднятого над землей

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

Работа и изменение потенциальной энергии упруго деформированного тела

Работа силы упругости равна изменению потенциальной энергии, взятому с противоположным знаком.

Кинетическая энергия

Кинетическая энергия – это энергия, которой обладает тело вследствие своего движения.

Обозначение – ( W_k (E_k) ), единицы измерения – Дж.

Кинетическая энергия равна половине произведения массы тела на квадрат его скорости:

Важно!
Так как кинетическая энергия отдельного тела определяется его массой и скоростью, то она не зависит от того, взаимодействует ли это тело с другими телами или нет. Значение кинетической энергии зависит от выбора системы отсчета, как и значение скорости. Кинетическая энергия системы тел равна сумме кинетических энергий отдельных тел, входящих в эту систему.

Потенциальная энергия

Потенциальная энергия – это энергия взаимодействия тел или частей одного и того же тела.

Обозначение – ( W_p (E_p) ), единицы измерения – Дж.

Потенциальная энергия тела, поднятого на некоторую высоту над землей, равна произведению массы тела, ускорения свободного падения и высоты, на которой он находится:

Потенциальная энергия упруго деформированного тела равна половине произведения жесткости на квадрат удлинения:

Важно!
Величина потенциальной энергии зависит от выбора нулевого уровня. Нулевым называется уровень, на котором потенциальная энергия равна нулю. Нулевой уровень выбирается произвольно, исходя из удобства решения задачи.

Закон сохранения механической энергии

Полная механическая энергия – это энергия, равная сумме кинетической и потенциальной энергий.

Обозначение – ( W (E) ), единицы измерения – Дж.

Закон сохранения механической энергии
В замкнутой системе тел, между которыми действуют только консервативные силы, механическая энергия сохраняется, т. е. не изменяется с течением времени:

Если между телами системы действуют кроме сил тяготения и упругости другие силы, например сила трения или сопротивления, действие которых приводит к превращению механической энергии в тепловую, то в такой системе тел закон сохранения механической энергии не выполняется.

Важно!
В случае, если кроме консервативных сил (тяжести, упругости, тяготения) существуют еще и неконсервативные силы, например сила трения, а также внешние силы, то

Теорема о кинетической энергии справедлива для сил любой природы:

Если на систему тел действуют неконсервативные и внешние силы, то изменение полной энергии равно сумме работ неконсервативных и внешних сил.

Закон сохранения и превращения энергии
Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой или передается от одного тела к другому.

Основные формулы по теме «Законы сохранения в механике»

Законы сохранения в механике

3.1 (62.98%) 47 votes

Источник

Относительный импульс

Изменение импульса тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Абсолютно упругий удар

Пуля пробила стенку

Радиус-вектор тела повернул на 180 градусов

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Второй закон Ньютона в импульсном виде

Реактивное движение

Суммарный импульс системы тел

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Сохранение проекции импульса

Как определить суммарный импульс?

Решение.

Ответ: p = mv^2.

Законы сохранения в механике

Импульс тела

Импульс системы тел

Закон сохранения импульса

Работа силы

Мощность

Работа как мера изменения энергии

Кинетическая энергия

Потенциальная энергия

Закон сохранения механической энергии

Основные формулы по теме «Законы сохранения в механике»

Не пропустите также: