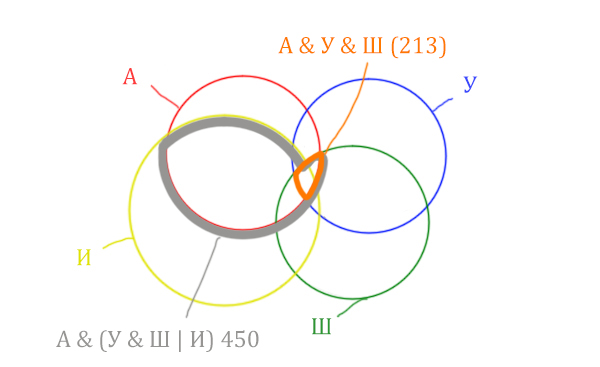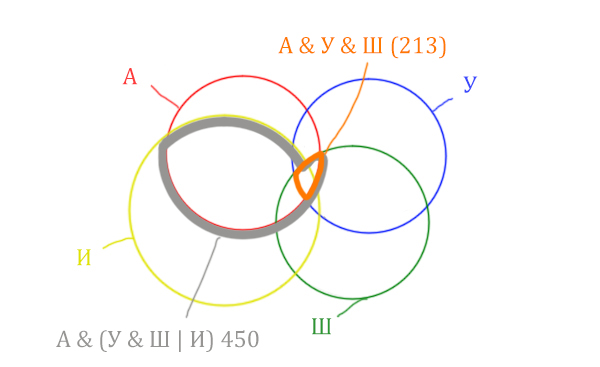Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
Задача (Простая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Видим, что по запросу «Пушкин» в поисковике нашлось 3500 страниц. По запросу «Лермонтов» — 2000 страниц.
Запрос «Пушкин | Лермонтов» обозначает, что поисковик выдаст страницы, где есть слова про «Пушкина», и страницы, где есть слова про «Лермонтова», а так же могут быть страницы, где написано и про «Пушкина», и про «Лермонтова» одновременно.
Если сложить страницы, в которых написано про «Пушкина» и про «Лермонтова» получается 3500 + 2000 = 5500 страниц. Но почему же при запросе «Пушкин | Лермонтов» получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про «Пушкина» (3500 страниц), мы подсчитали и те страницы, где было написано и про «Пушкина», и про «Лермонтова» одновременно.
Тоже самое и для количества страниц, где написано про «Лермонтова» (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про «Пушкина», и про «Лермонтова».
В вопросе спрашивается, сколько страниц будет по запросу «Пушкин & Лермонтов«. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».
Отсюда получается:
Пушкин & Лермонтов = (3500 + 2000) — 4500 = 5500 — 4500 = 1000 страниц.
Это и будет ответ!
Теперь решим эту задачу с помощью Кругов Эйлера!
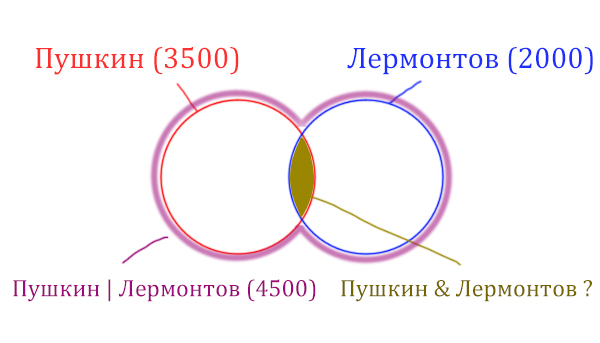
У нас всего есть две сущности: «Пушкин» и «Лермонтов». Поэтому рисуем два пересекающихся круга, желательно разными цветами.
Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию «Пушкин | Лермонтов». Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» «Пушкин | Лермонтов» (4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
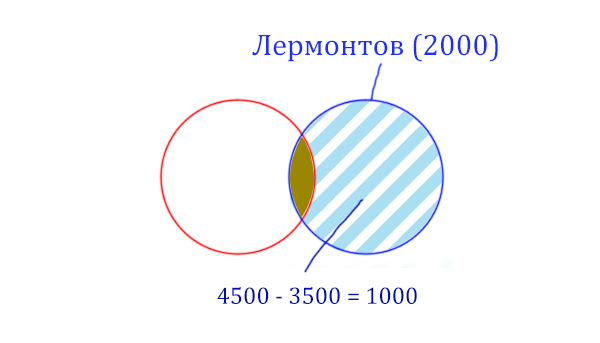
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 — 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Ответ: 1000
Рассмотрим ещё одну не сложную разминочную задачу.
Задача (Разминочная)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
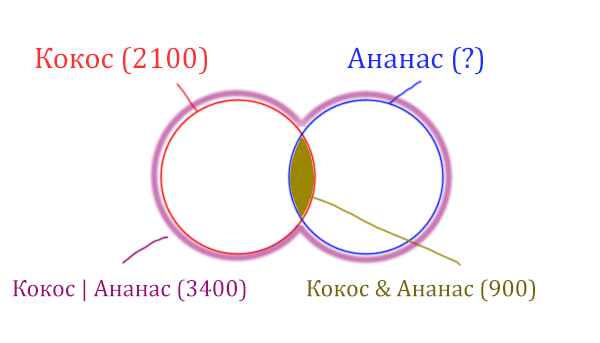
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.
Найдём заштрихованную часть красного круга.
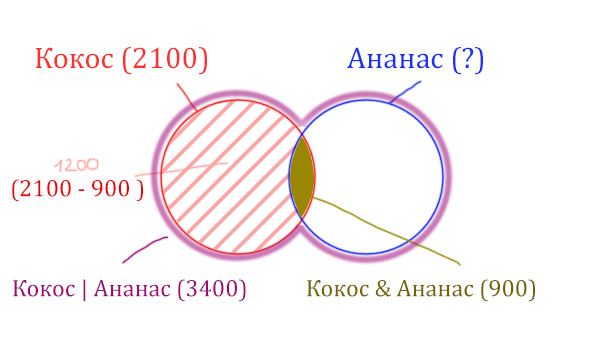
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 — 900 = 1200.
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 — 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
Задача (Классическая)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
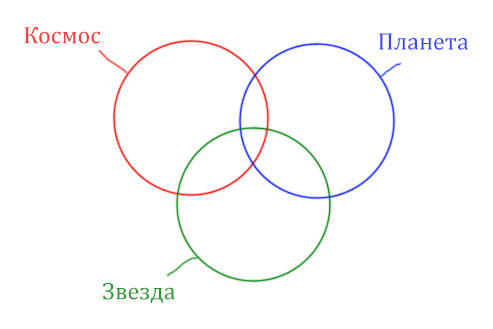
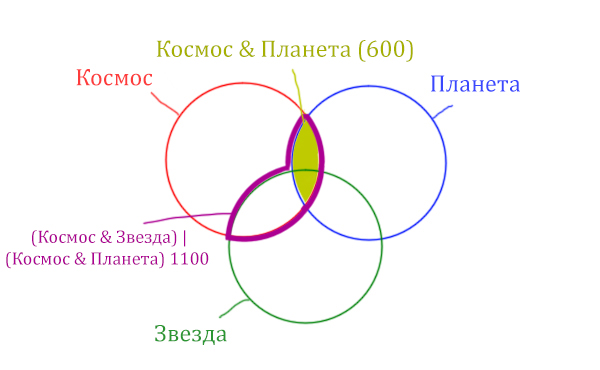
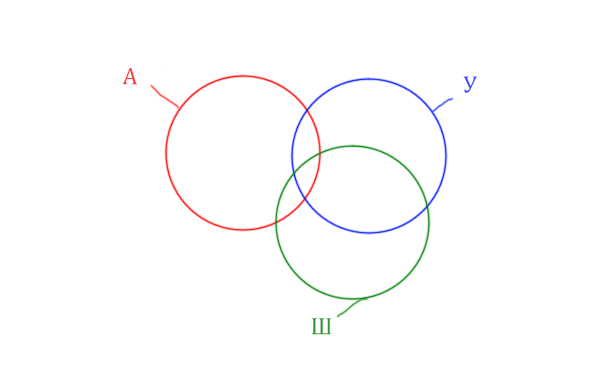
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического «ИЛИ».
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
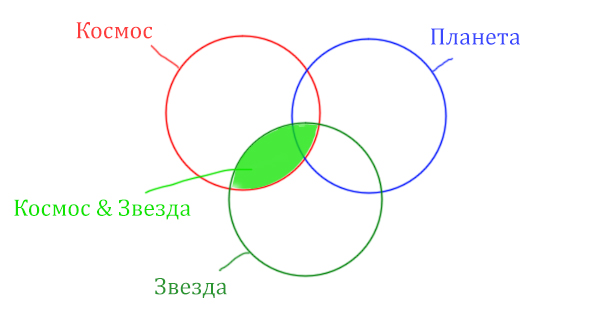
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
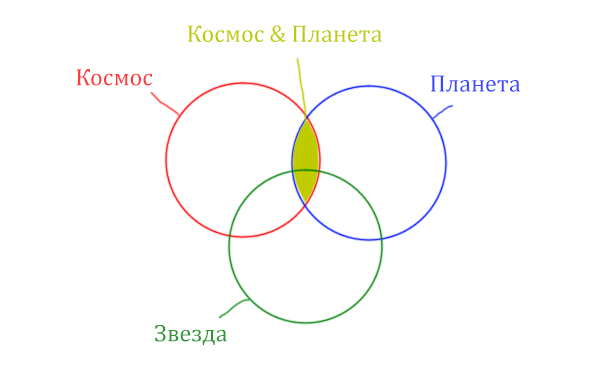
Теперь отметим вторую скобку Космос & Планета.
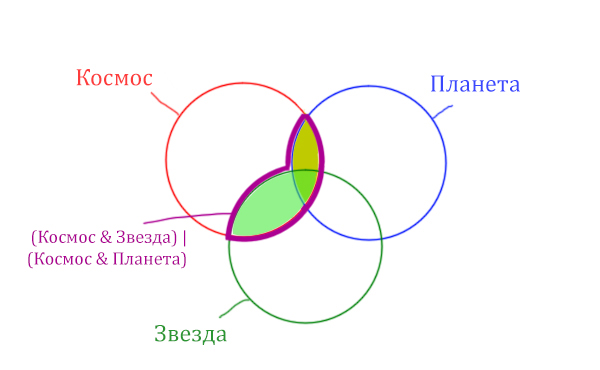
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического «ИЛИ». Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
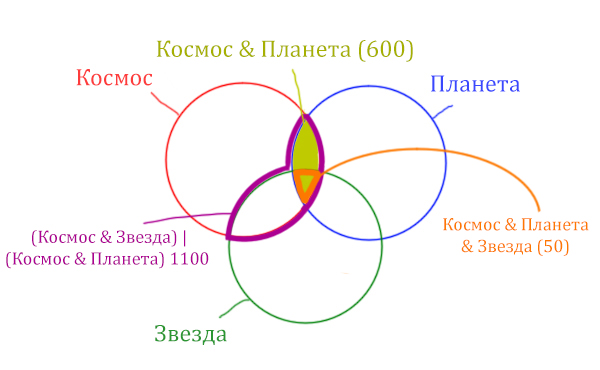
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
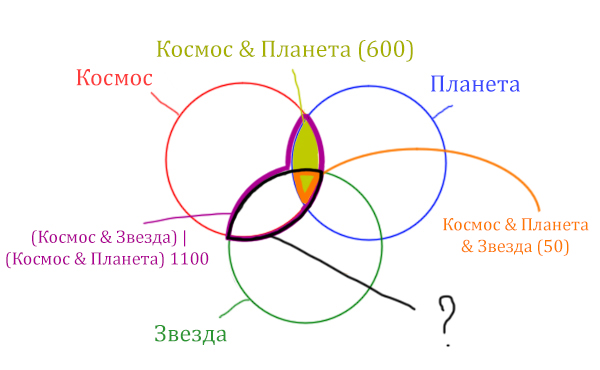
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
Теперь у нас есть все компоненты, чтобы решить эту задачу.
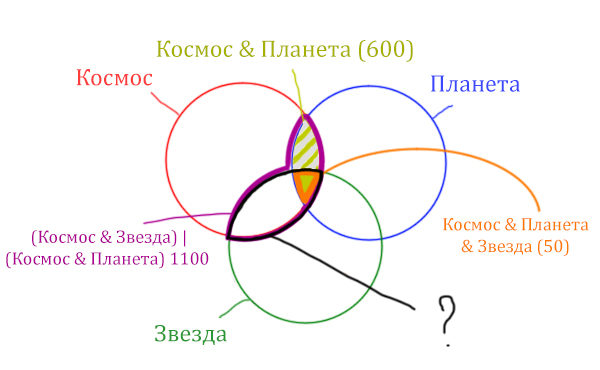
Найдём заштрихованную область.
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 — 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 — 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
Задача (На закрепление)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
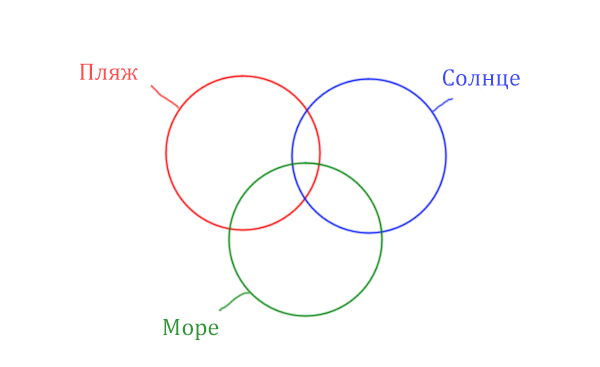
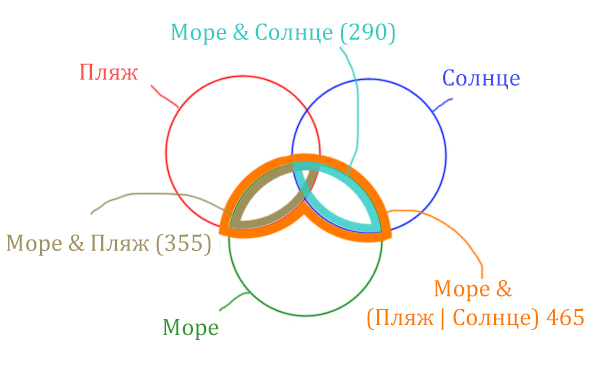
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
Отметим все области для которых нам даны количество страниц.
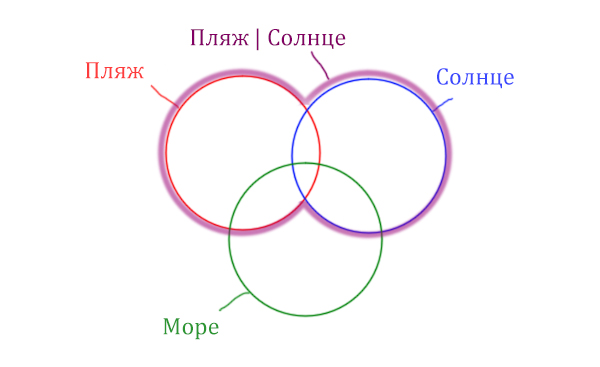
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)
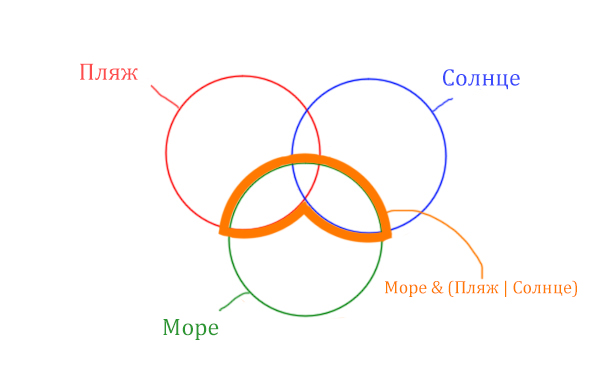
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
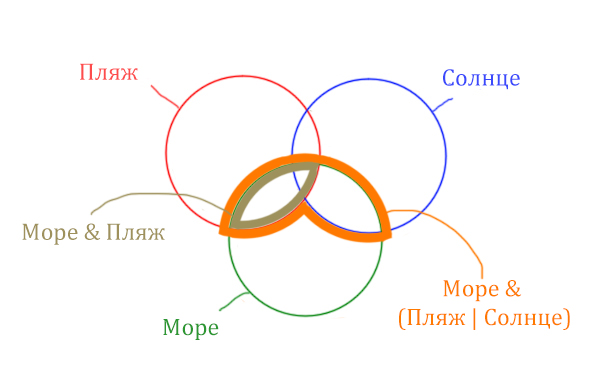
Теперь отметим Море & Пляж.
Теперь отметим Море & Солнце.
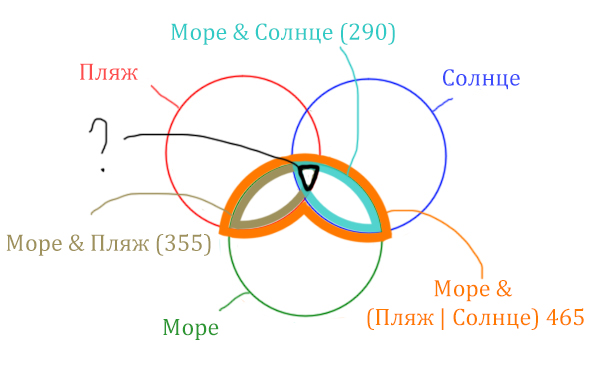
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
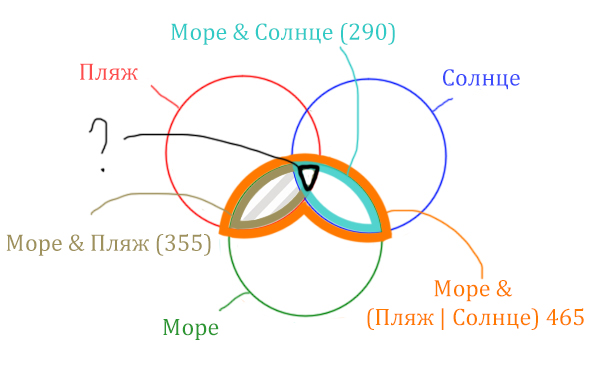
Найдём заштрихованную область!
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) — Море & Солнце =
= 465 — 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) — Количество страниц (в заштрихованной области) 175 =
= 355 — 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.
Задача (с 4 сущностями)
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Англия & Ирландия?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
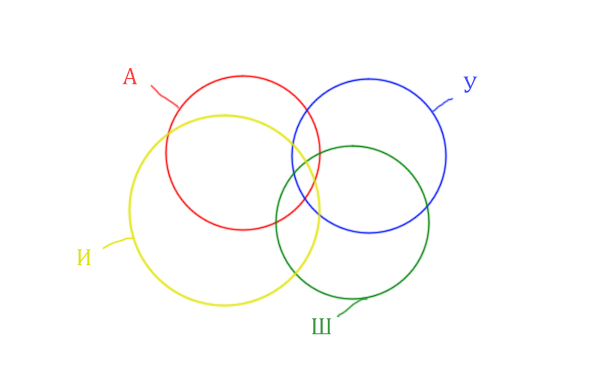
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
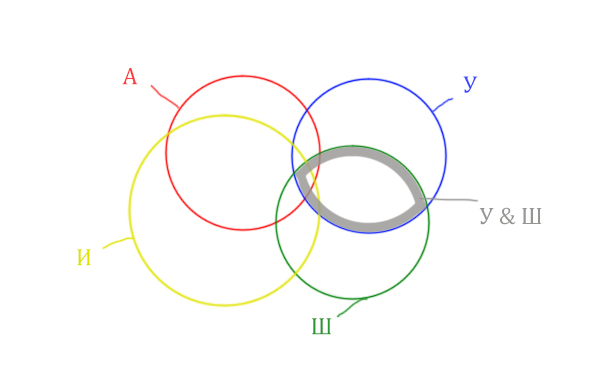
Область Уэльс & Шотландия выглядит так:
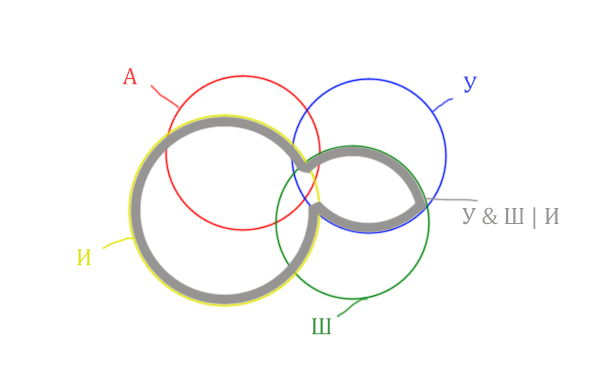
Добавим к этой области Ирландию через логическое «ИЛИ». Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
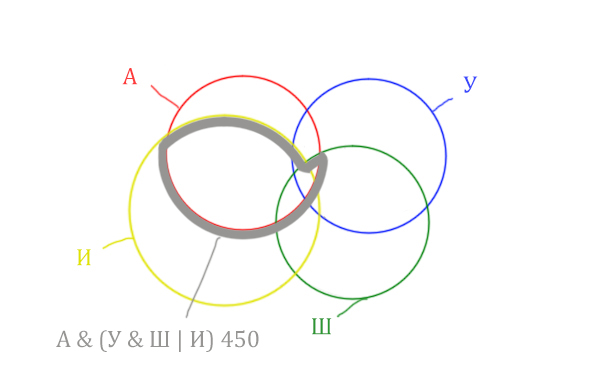
Теперь нужно сделать операцию логического «И» получившийся области с «Англией». Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
Т.е. это общее между предыдущем серым контуром и красным кругом!
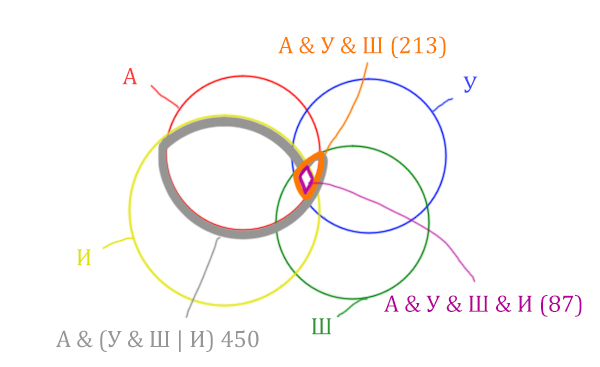
Отметим Англия & Уэльс & Шотландия — это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
Отметим Англия & Уэльс & Шотландия & Ирландия — это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
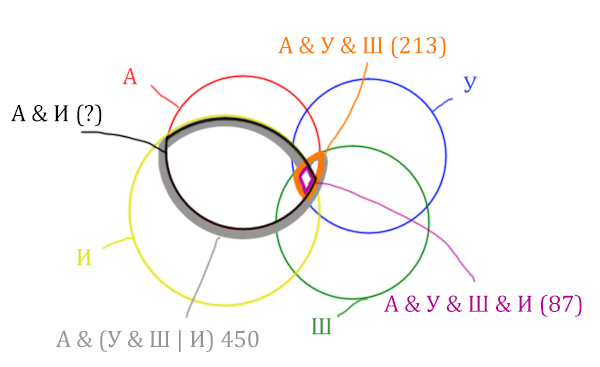
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
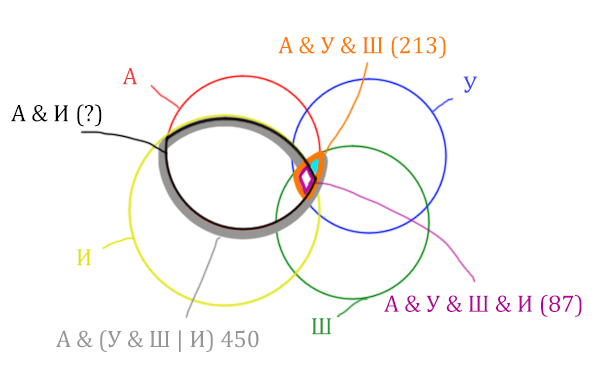
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) — Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 — 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) — Количество (для бирюзового кусочка) =
450 — 126 = 324
Это и будет ответ!
Ответ: 324.
Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
Задача (ЕГЭ по информатике, 2019, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Суфле | Корзина | Эклер
Решение:
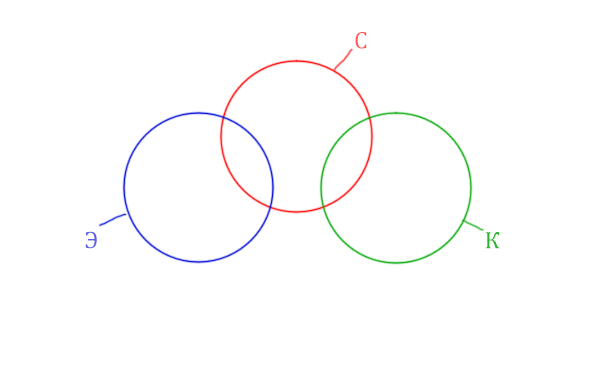
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое «И» между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
Отметим всё, что нам дано в условии.
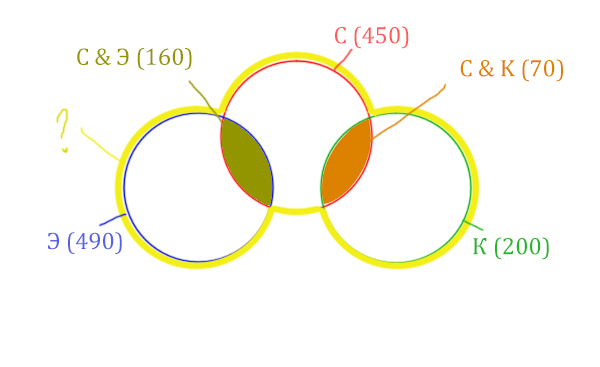
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
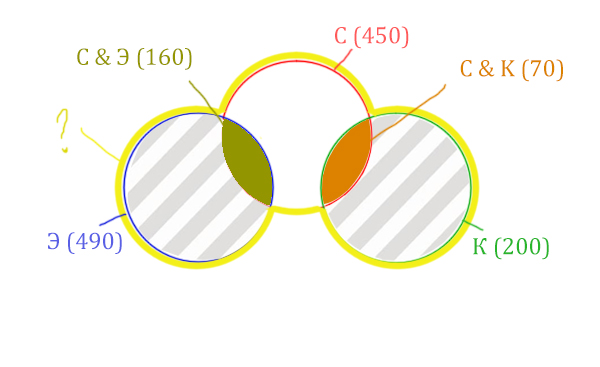
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) — Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) — Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Ответ: 910
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Аврора & Крейсер
Решение:
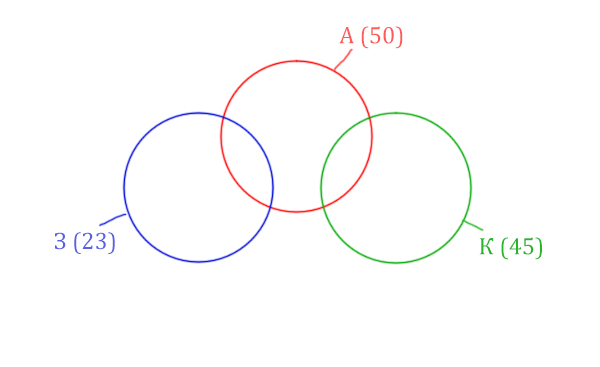
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.
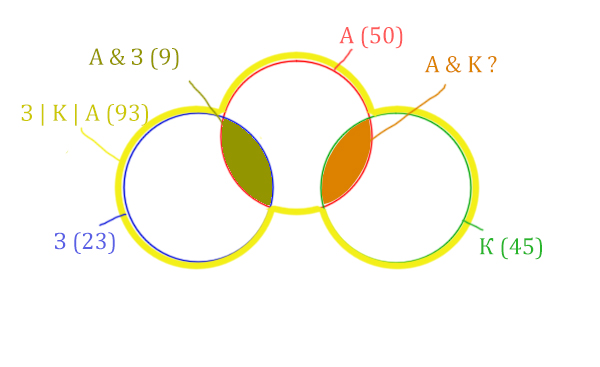
Нарисуем все данные на рисунке.
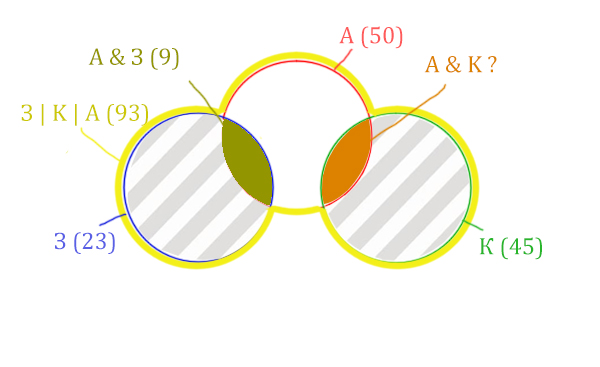
Нужно найти для начала заштрихованную правую часть.
Количество страниц (для двух заштрих. частей) =
З | К | А (93) — Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) — А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) — Колич. страниц (для лев. заштрих. части) (14) =
= 43 — 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) — Колич. страниц (для правой заштрих. части) (29) =
45 — 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
Интересно…
как быть , когда идет произведение3 предметов + произведниее 3 педметов..
ОГРОМНОЕ СПАСИБО за Ваш труд!!! Всё очень понятно и доходчиво. +++++++++++++++
Круги Эйлера в информатике
Сегодня разберём задачи на круги Эйлера в информатике.
Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Пушкин | 3500 |
| Лермонтов | 2000 |
| Пушкин | Лермонтов | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Видим, что по запросу «Пушкин» в поисковике нашлось 3500 страниц. По запросу «Лермонтов» — 2000 страниц.
Запрос «Пушкин | Лермонтов» обозначает, что поисковик выдаст страницы, где есть слова про «Пушкина», и страницы, где есть слова про «Лермонтова», а так же могут быть страницы, где написано и про «Пушкина», и про «Лермонтова» одновременно.
Если сложить страницы, в которых написано про «Пушкина» и про «Лермонтова» получается 3500 + 2000 = 5500 страниц. Но почему же при запросе «Пушкин | Лермонтов» получается меньше страниц, всего 4500 ?
Этот факт обозначает то, что когда мы подсчитывали страницы про «Пушкина» (3500 страниц), мы подсчитали и те страницы, где было написано и про «Пушкина», и про «Лермонтова» одновременно.
Тоже самое и для количества страниц, где написано про «Лермонтова» (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про «Пушкина», и про «Лермонтова».
В вопросе спрашивается, сколько страниц будет по запросу «Пушкин & Лермонтов«. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».
Пушкин & Лермонтов = (3500 + 2000) — 4500 = 5500 — 4500 = 1000 страниц.
Это и будет ответ!
Теперь решим эту задачу с помощью Кругов Эйлера!
У нас всего есть две сущности: «Пушкин» и «Лермонтов». Поэтому рисуем два пересекающихся круга, желательно разными цветами.
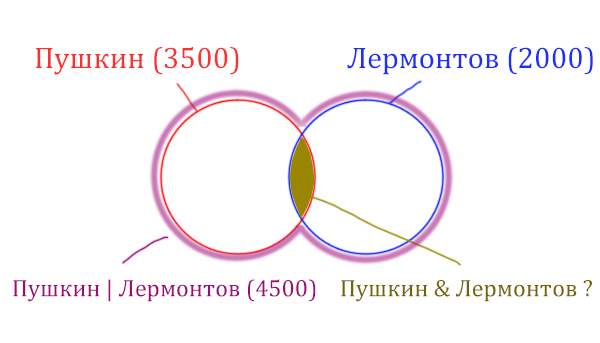
Объединение двух кругов в общую фигуру ( показано фиолетовым цветом), показывает операцию «Пушкин | Лермонтов». Эта операция всегда стремится увеличить площадь, объединить площади других фигур!
Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» «Пушкин | Лермонтов» (4500).
Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.
Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).
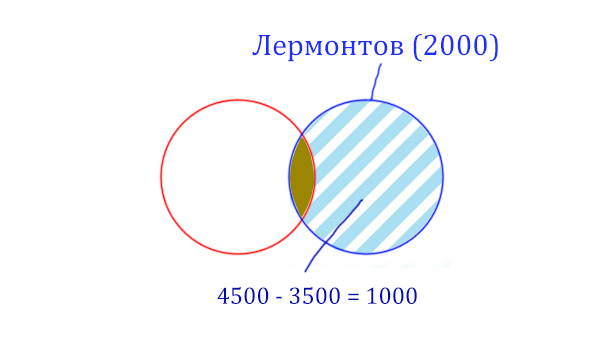
Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:
Пушкин & Лермонтов (Количество страниц) = 2000 — 1000 = 1000
Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.
Рассмотрим ещё одну не сложную разминочную задачу.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Кокос | Ананас | 3400 |
| Кокос & Ананас | 900 |
| Кокос | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Ананас?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.
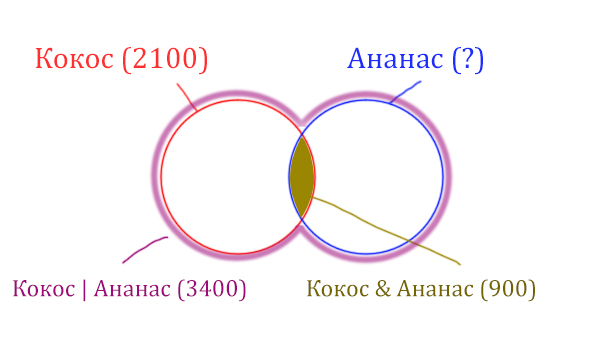
Найдём заштрихованную часть красного круга.
Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 — 900 = 1200.
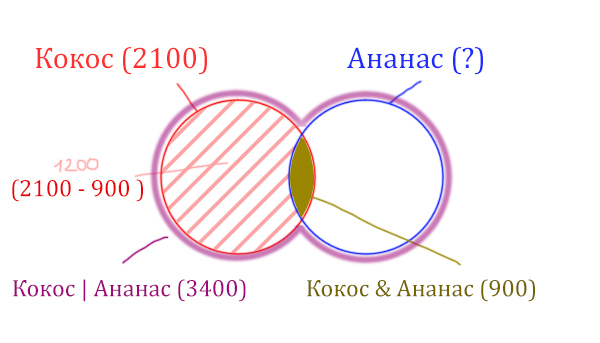
После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!
Ананас (Количество страниц) = 3400 — 1200 = 2200
Ответ: 2200
Разберём классическую задачу из информатики по кругам Эйлера.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| (Космос & Звезда) | (Космос & Планета) | 1100 |
| Космос & Планета | 600 |
| Космос & Планета & Звезда | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Космос & Звезда?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.
Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического «ИЛИ».
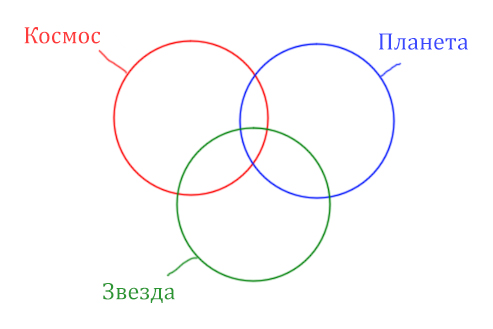
Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).
Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда
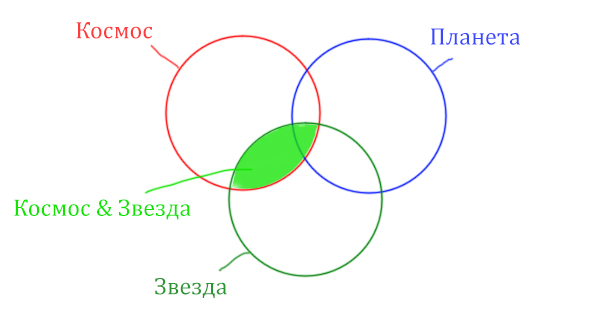
Теперь отметим вторую скобку Космос & Планета.
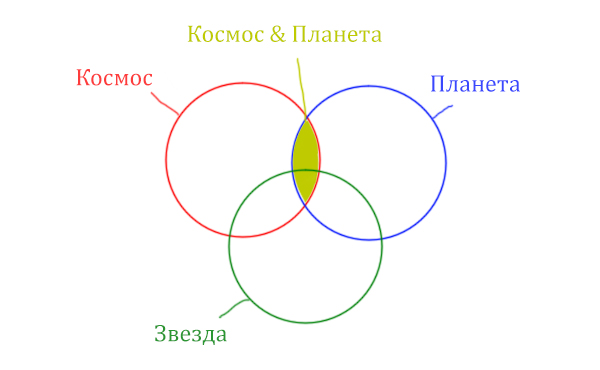
В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического «ИЛИ». Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!
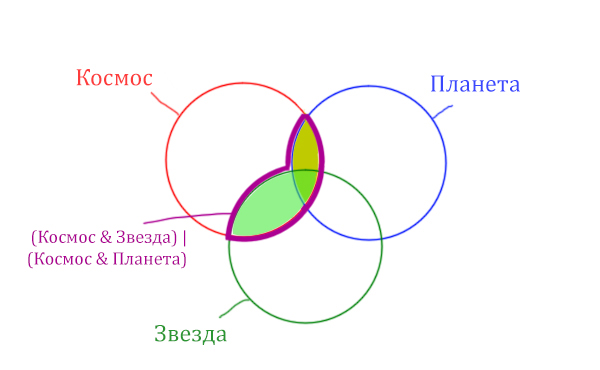
Отметим Космос & Планета ещё раз, т.к. для этого выражения известно количество страниц.
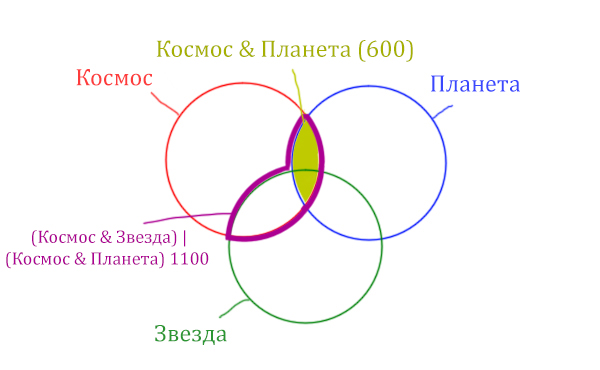
Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!
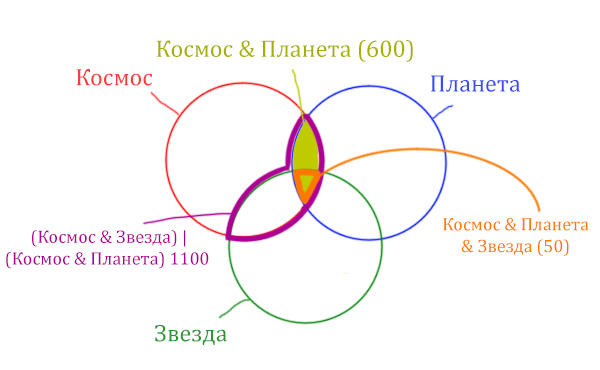
Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.
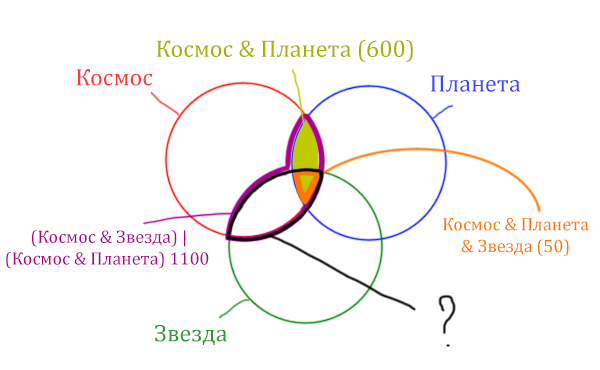
Теперь у нас есть все компоненты, чтобы решить эту задачу.
Найдём заштрихованную область.
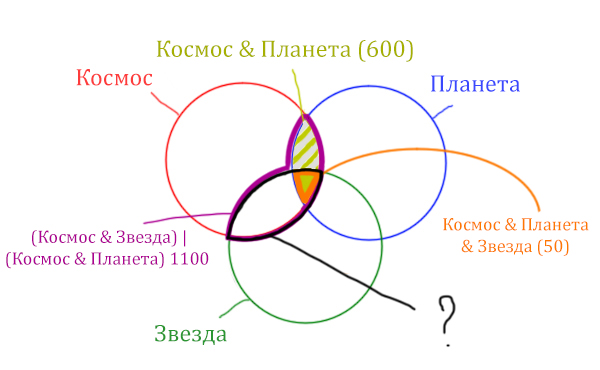
Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).
Количество страниц в заштрихованной части = 600 — 50 = 550
Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).
Количество страниц (при запросе Космос & Звезда) = 1100 — 550 = 550
Ответ: 550
Закрепляем материал по задачам на Круги Эйлера.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Море & Солнце | 290 |
| Море & Пляж | 355 |
| Море & (Пляж | Солнце) | 465 |
Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.
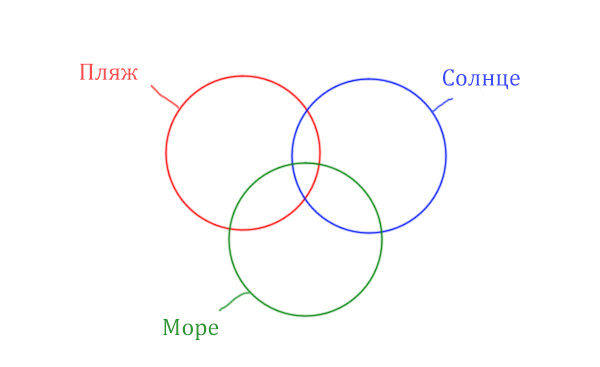
Отметим все области для которых нам даны количество страниц.
В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце) 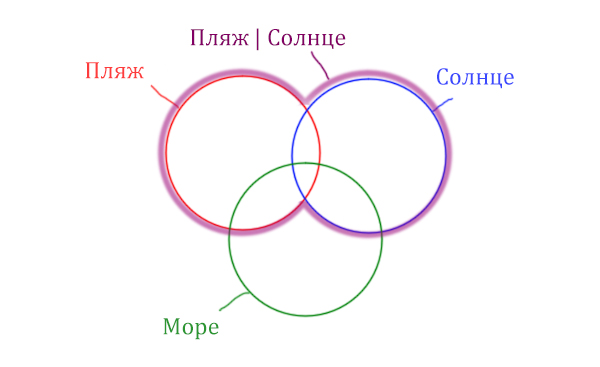
Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.
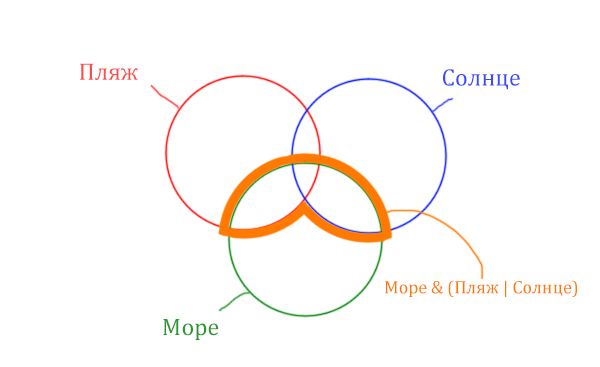
Теперь отметим Море & Пляж.
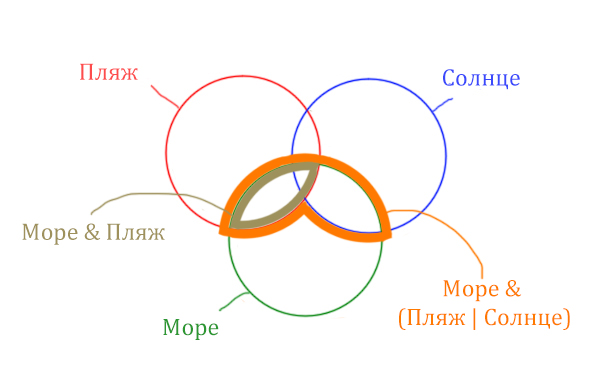
Теперь отметим Море & Солнце.
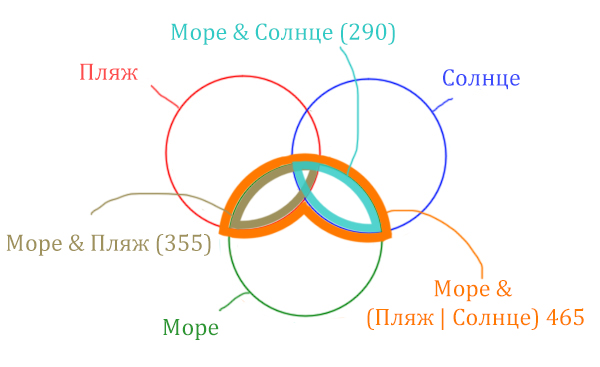
Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!
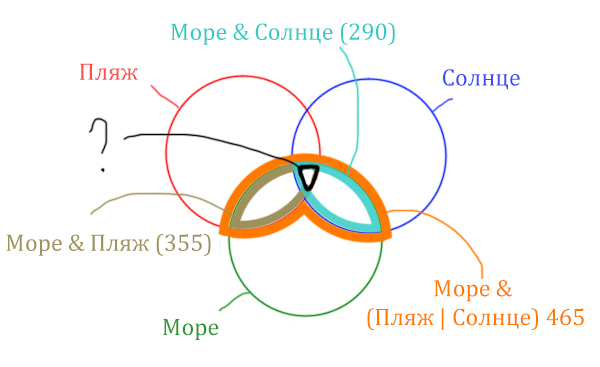
Найдём заштрихованную область!
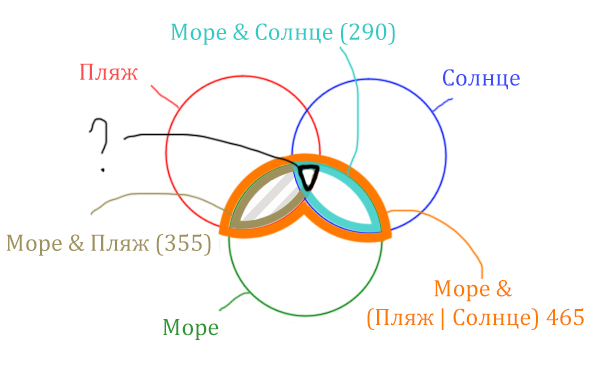
Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) — Море & Солнце =
= 465 — 290 = 175
Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).
Количество страниц (Море & Пляж & Солнце) =
= Море & Пляж (355) — Количество страниц (в заштрихованной области) 175 =
= 355 — 175 = 180
Ответ: 180
Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
| Англия & (Уэльс & Шотландия | Ирландия) | 450 |
| Англия & Уэльс & Шотландия | 213 |
| Англия & Уэльс & Шотландия & Ирландия | 87 |
Какое количество страниц (в тысячах) будет найдено по запросу
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.
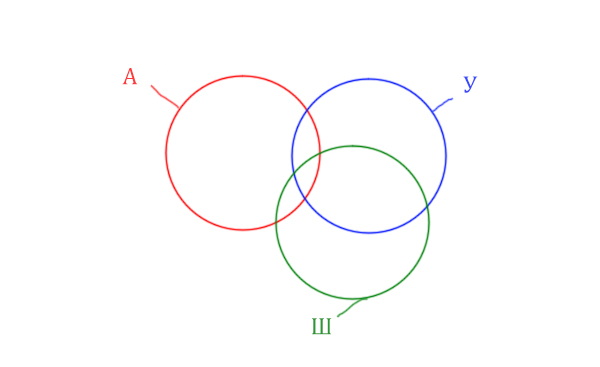
Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.
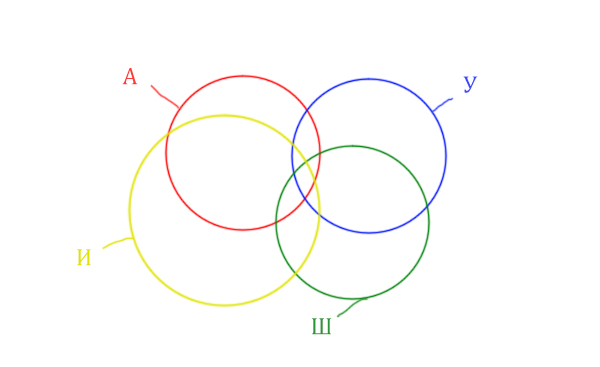
Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.
Область Уэльс & Шотландия выглядит так:
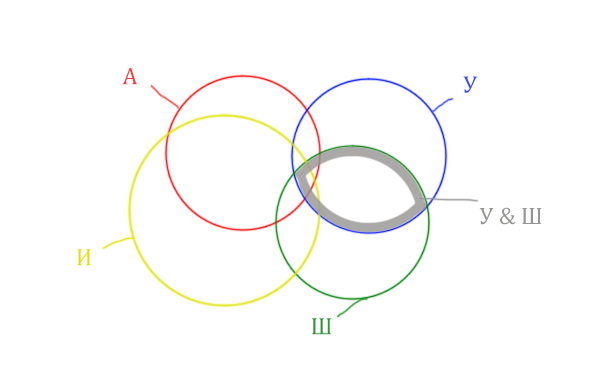
Добавим к этой области Ирландию через логическое «ИЛИ». Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!
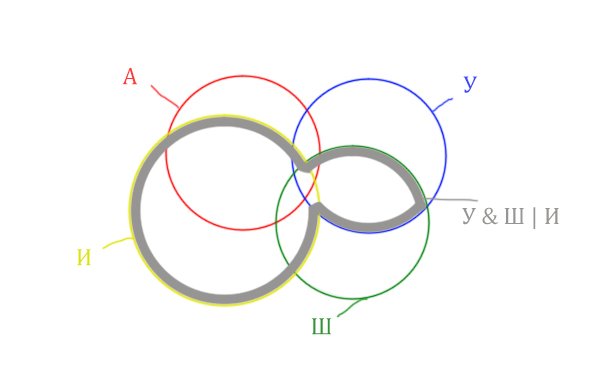
Теперь нужно сделать операцию логического «И» получившийся области с «Англией». Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:
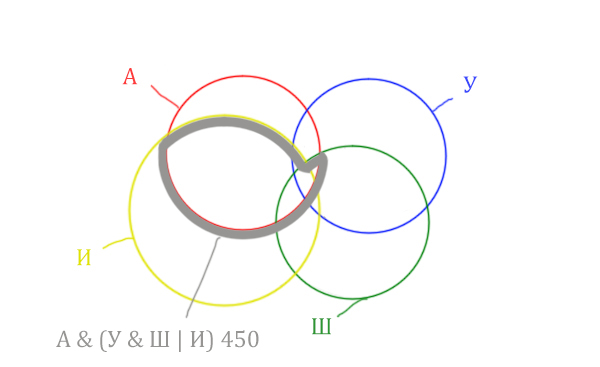
Т.е. это общее между предыдущем серым контуром и красным кругом!
Отметим Англия & Уэльс & Шотландия — это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.
Отметим Англия & Уэльс & Шотландия & Ирландия — это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.
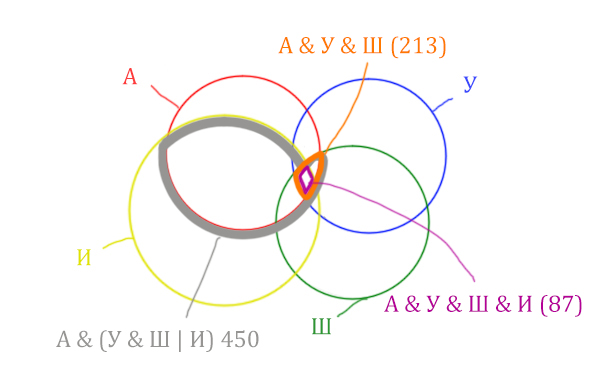
Отметим то, что нужно найти Англия & Ирландия чёрным цветом.
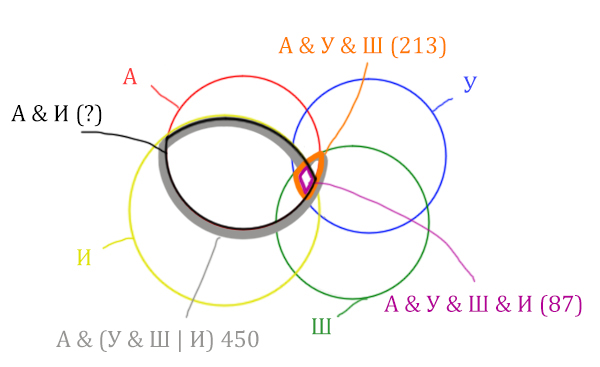
Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!
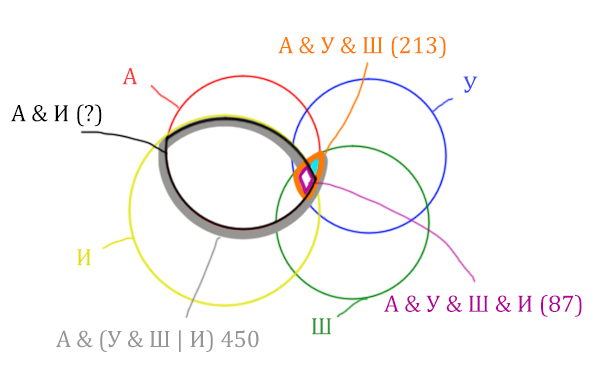
Найдём, сколько страниц приходится на бирюзовый кусочек:
Количество страниц (для бирюзового кусочка) =
= Англия & Уэльс & Шотландия (213) — Англия & Уэльс & Шотландия & Ирландия (87) =
= 213 — 87 = 126
Найдём искомую чёрную область.
Количество станиц (для чёрной области) =
= Англия & (Уэльс & Шотландия | Ирландия) (450) — Количество (для бирюзового кусочка) =
450 — 126 = 324
Это и будет ответ!
Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)
Задача (ЕГЭ по информатике, 2019, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Суфле | 450 |
| Корзина | 200 |
| Эклер | 490 |
| Суфле & Корзина | 70 |
| Суфле & Эклер | 160 |
| Корзина & Эклер | 0 |
Сколько страниц (в тысячах) будет найдено по запросу
Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!
Так же видим, что логическое «И» между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.
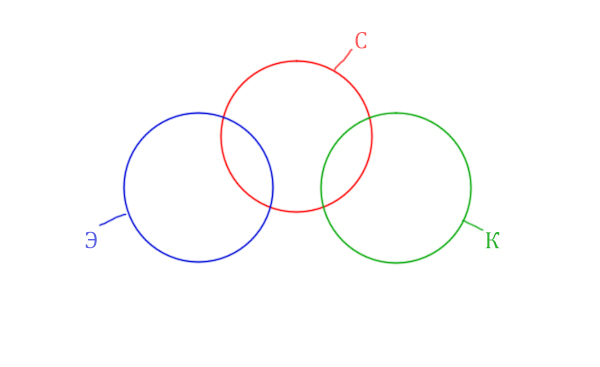
Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.
Отметим всё, что нам дано в условии.
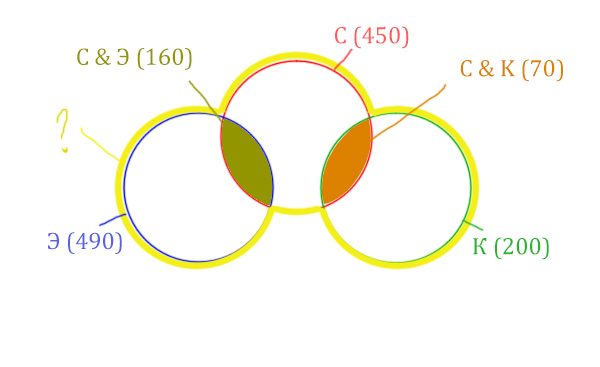
Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.
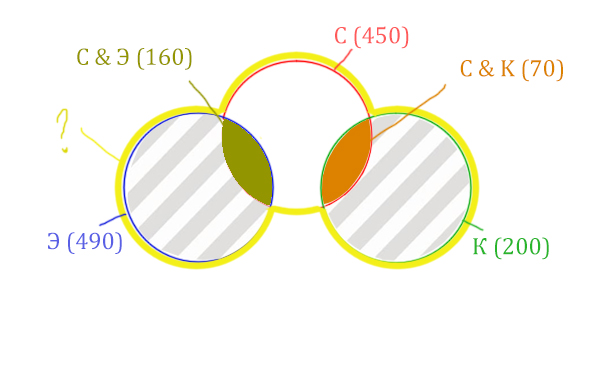
Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.
Левая заштрихованная область находится просто:
Количество страниц (лев. заштрих. область) =
= Эклер (490) — Суфле & Эклер (160) = 330
Так же найдём площадь правой заштрихованной области:
Количество страниц (прав. заштрих. область) =
= Корзина (200) — Суфле & Корзина (70) = 130
Теперь можно найти искомую жёлтую область
Количество страниц (Суфле | Корзина | Эклер) =
= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =
= 450 + 330 + 130 = 910
Задача решена, можно писать ответ.
Разберём ещё одну задачу из реального ЕГЭ уже 2020 года
Задача (ЕГЭ по информатике, 2020, Москва)
В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:
| Запрос | Найдено страниц (в тысячах) |
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу
Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.
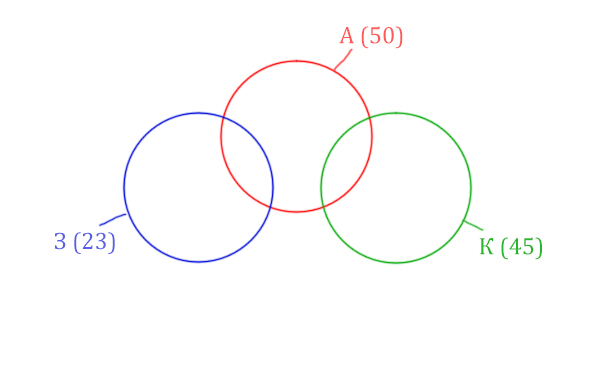
Нарисуем все данные на рисунке.
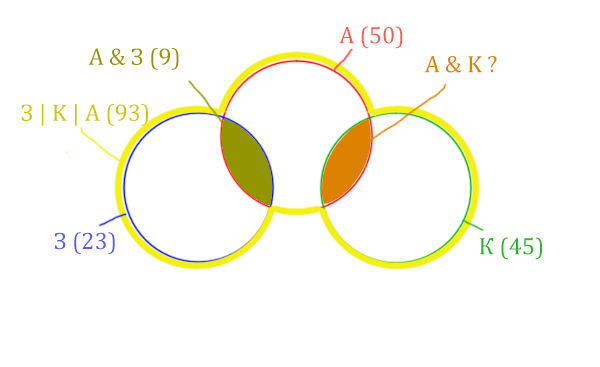
Нужно найти для начала заштрихованную правую часть.
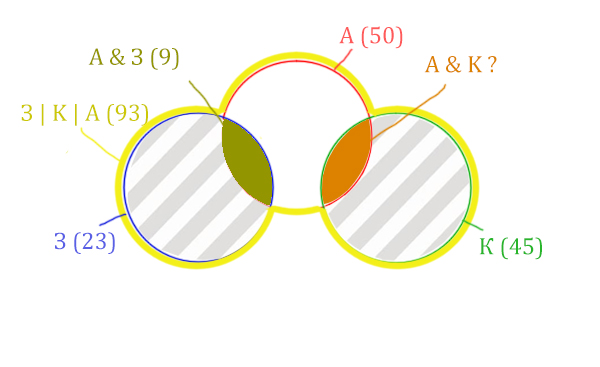
Количество страниц (для двух заштрих. частей) =
З | К | А (93) — Красный круг (50) = 43
Левую заштрихованную область легко найти.
Количество страниц (для левой заштрих. части) =
Синий круг (23) — А & З (9) = 14
Тогда для правой заштрихованной области получается:
Колич. страниц (для правой заштрих. части) =
Колич. страниц (для двух заштрих. частей) (43) — Колич. страниц (для лев. заштрих. части) (14) =
= 43 — 14 = 29
Тогда искомую область легко найти:
Колич. страниц (А & K) =
Зелёный круг (45) — Колич. страниц (для правой заштрих. части) (29) =
45 — 29 = 16
Ответ: 16
На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.
Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ
В курсе Информатики и ИКТ основной и старшей школы рассматриваются такие важные темы как “Основы логики” и “Поиск информации в Интернет”. При решении определенного типа задач удобно использовать круги Эйлера (диаграммы Эйлера-Венна).
Математическая справка. Диаграммы Эйлера-Венна используются прежде всего в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2 n комбинаций n свойств. Например, при n=3 диаграмма Эйлера-Венна обычно изображается в виде трех кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
2. Представление логических связок в поисковых запросах
При изучении темы “Поиск информации в Интернет” рассматриваются примеры поисковых запросов с использованием логических связок, аналогичным по смыслу союзам “и”, “или” русского языка. Смысл логических связок становится более понятным, если проиллюстрировать их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).
| Логическая связка | Пример запроса | Пояснение | Круги Эйлера |
| & — “И” | Париж & университет | Будут отобраны все страницы, где упоминаются оба слова: Париж и университет | Рис.1 |
| — “ИЛИ”
Париж | университет
Будут отобраны все страницы, где упоминаются слова Париж и/или университет
Рис.2
3. Связь логических операций с теорией множеств
С помощью диаграмм Эйлера-Венна можно наглядно представить связь логических операций с теорией множеств. Для демонстрации можно воспользоваться слайдами в Приложение 1.
Логические операции задаются своими таблицами истинности. В Приложении 2 подробно рассматриваются графические иллюстрации логических операций вместе с их таблицами истинности. Поясним принцип построения диаграммы в общем случае. На диаграмме – область круга с именем А отображает истинность высказывания А (в теории множеств круг А – обозначение всех элементов, входящих в данное множество). Соответственно, область вне круга отображает значение “ложь” соответствующего высказывания. Что бы понять какая область диаграммы будет отображением логической операции нужно заштриховать только те области, в которых значения логической операции на наборах A и B равны “истина”.
Например, значение импликации равно “истина” в трех случаях (00, 01 и 11). Заштрихуем последовательно: 1) область вне двух пересекающихся кругов, которая соответствует значениям А=0, В=0; 2) область, относящуюся только к кругу В (полумесяц), которая соответствует значениям А=0, В=1; 3) область, относящуюся и к кругу А и к кругу В (пересечение) – соответствует значениям А=1, В=1. Объединение этих трех областей и будет графическим представлением логической операции импликации.
4. Использование кругов Эйлера при доказательстве логических равенств (законов)
Для того, чтобы доказать логические равенства можно применить метод диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон де Моргана).
Для наглядного представления левой части равенства выполним последовательно: заштрихуем оба круга (применим дизъюнкцию) серым цветом, затем для отображения инверсии заштрихуем область за пределами кругов черным цветом:
Рис.3 
Для визуального представления правой части равенства выполним последовательно: заштрихуем область для отображения инверсии (¬А) серым цветом и аналогично область ¬В также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):
Рис.5 

Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.
5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск информации в Интернет”
Задача №18 из демо-версии ГИА 2013.
В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код – соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
| Код | Запрос |
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
Для каждого запроса построим диаграмму Эйлера-Венна:
Запрос Б
Запрос В
Запрос Г
Задача В12 из демо-версии ЕГЭ-2013.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысяч) |
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ф – количество страниц (в тысячах) по запросу Фрегат;
Э – количество страниц (в тысячах) по запросу Эсминец;
Х – количество страниц (в тысячах) по запросу, в котором упоминается Фрегат и не упоминается Эсминец;
У – количество страниц (в тысячах) по запросу, в котором упоминается Эсминец и не упоминается Фрегат.
Построим диаграммы Эйлера-Венна для каждого запроса:
| Запрос | Диаграмма Эйлера-Венна | Количество страниц |
| Фрегат | Эсминец | Рис.12 |
3400
Фрегат & Эсминец
Рис.13
900
Фрегат
Рис.14
2100
Эсминец
Рис.15
?
Согласно диаграммам имеем:
- Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
- Э = 900+У = 900+1300= 2200.
6. Решение логических содержательных задач методом диаграмм Эйлера-Венна
В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14 человек, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек — и математический и физический, 5 и математический и химический, 3 — и физический и химический.
Сколько учеников класса не посещают никаких кружков?
Для решения данной задачи очень удобным и наглядным является использование кругов Эйлера.
Самый большой круг – множество всех учеников класса. Внутри круга три пересекающихся множества: членов математического (М), физического (Ф), химического (Х) кружков.
Пусть МФХ – множество ребят, каждый из которых посещает все три кружка. МФ¬Х – множество ребят, каждый из которых посещает математический и физический кружки и не посещает химический. ¬М¬ФХ — множество ребят, каждый из которых посещает химический кружок и не посещает физический и математический кружки.
Аналогично введем множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Известно, что все три кружка посещают 2 человека, следовательно, в область МФХ впишем число 2. Т.к. 8 человек посещают и математический и физический кружки и среди них уже есть 2 человека, посещающих все три кружка, то в область МФ¬Х впишем 6 человек (8-2). Аналогично определим количество учащихся в остальных множествах:
Круги Эйлера с названиями непересекающихся множеств:
Круги Эйлера с количественной информацией:
Например, количество человек, которые посещают физический кружок 2+6+1+5=14
Просуммируем количество человек по всем областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из класса посещают кружки.
Значит, 36-28 = 8 учеников не посещают кружки.
После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино. ни в театре, ни в цирке. В кино побывало 25 человек, в театре — 11, в цирке 17 человек; и в кино, и в театре — 6; и в кино и в цирке — 10; и в театре и в цирке — 4.
Сколько человек побывало и в кино, и в театре, и в цирке?
Пусть х – количество ребят, которые побывали и в кино, и в театре, и в цирке.
Тогда можно построить следующую диаграмму и посчитать количество ребят в каждой области:
В кино и театре побывало 6 чел., значит, только в кино и театре (6-х) чел.
Аналогично, только в кино и цирке (10-х) чел.
Только в театре и цирке (4-х) чел.
В кино побывало 25 чел., значит, из них только в кино были 25 — (10-х) – (6-х) – х = (9+х).
Аналогично, только в театре были (1+х) чел.
Только в цирке были (3+х) чел.
Не были в театре, кино и цирке – 2 чел.
Значит, 36-2=34 чел. побывали на мероприятиях.
С другой стороны можем просуммировать количество человек, которые были в театре, кино и цирке:
Отсюда следует, что только один человек побывал на всех трех мероприятиях.
Таким образом, круги Эйлера (диаграммы Эйлера-Венна) находят практическое применение при решении задач в формате ЕГЭ и ГИА и при решении содержательных логических задач.
Интегрированный урок (информатика + математика). «Исследование окружности в среде Лого» 6 класс
«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Выберите документ из архива для просмотра:
Выбранный для просмотра документ Mochalova_pismo.doc
Автор: Мочалова Марина Владимировна
Должность: учитель информатики и ИКТ
Образовательное учреждение: лицей №144
г. Санкт-Петербург, Калининский район
Автор: Фомина Ирина Олеговна
Должность: учитель математики
Образовательное учреждение: лицей №144
г. Санкт-Петербург, Калининский район
Выбранный для просмотра документ Mochalova_prezent.ppt
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Описание слайда:
Автор: Мочалова Марина Владимировна
Должность: учитель информатики и ИКТ
Категория: высшая
Образовательное учреждение: лицей №144
г. Санкт-Петербург, Калининский район
E-mail: cher56@yandex.ru
Автор: Фомина Ирина Олеговна
Должность: учитель математики
Категория: высшая
Образовательное учреждение: лицей №144
г. Санкт-Петербург, Калининский район
Интегрированный урок
«Информатика + математика»
Тема урока
«Исследование окружности
в среде ЛОГО»
(6 класс)
Описание слайда:
Какие из данных многоугольников являются правильными? Почему?
Тема урока: Исследование окружности
2
1
3
5
4
Правильным называется многоугольник, у которого все стороны равны и все углы равны.
Описание слайда:
Окружность – это множество точек, равноудаленных от ее центра.
Величина угла поворота Черепашки при построении правильного N-угольника вычисляется по формуле
Тема урока: исследование окружности в ЛОГО
Если у правильного многоугольника постепенно увеличивать количество вершин, на какую фигуру он становится похож?
Как бы вы определили, что такое «окружность»?
на окружность
Описание слайда:
Что такое окружность?
Помнить каждому нужно,
Что такое окружность.
Это множество точек,
Расположенных точно
На одном расстоянии,
Обратите внимание,
От одной только точки.
Помни смысл этой строчки.
Эта общая точка, по-дружески,
Называется центром окружности.
Тема урока: исследование окружности в ЛОГО
Описание слайда:
а) повтори 18 [вп 18 пр 20] или повтори 18 [вп 20 пр 20]?
б) повтори 18 [вп 20 пр 20] или повтори 20 [вп 18 пр 18]?
L1 = 20 шагов * 18 = 360 шагов L2 = 18 шагов * 20 = 360 шагов
одинаковы
Путь, который пройдет Черепашка при построении окружности, вычисляется по формуле: L = N * m
N – количество сторон правильного многоугольника
m – длина одной стороны многоугольника (в шагах)
L1 = 18 шагов * 18 = 324 шага L2 = 20 шагов * 18 = 360 шагов
Какая окружность будет большего размера и почему?
Тема урока: исследование окружности в ЛОГО
Описание слайда:
I. Для рисования правильного 10-угольника со стороной 20 шагов, нужно дать команду
1. повтори 20 [вп 10 пр 18]
2. повтори 10 [вп 20 пр 36]
15
повтори 6 [ вп 15 пр 60]
Тема урока: исследование окружности в ЛОГО
Описание слайда:
Тема урока: исследование окружности в ЛОГО
Описание слайда:
— нарисовать линию до начальной точки;
— из ИП нарисовать половинку окружности;
— повернуть голову Черепашки в направлении ИП;
— нарисовать половину окружности с поворотом головы Черепашки направо, затем вторую половинку с поворотом головы налево;
Алгоритм рисования мыши
— закрасить тело мышки серым цветом.
Тема урока: исследование окружности в ЛОГО
Описание слайда:
Выводы:
— для Черепашки окружностью является многоугольник с количеством сторон 36 и более;
— величина одного угла поворота головы Черепашки при построении правильного n-угольника вычисляется по формуле
— диаметр окружности – это отрезок, соединяющий 2 точки окружности и проходящий через ее центр;
— радиус окружности – это отрезок, соединяющий любую точку окружности с ее центром;
— радиус окружности равен половине диаметра;
— отношение длины окружности к ее диаметру есть величина постоянная, обозначается знаком и равна 3,14.
Тема урока: исследование окружности в ЛОГО
Описание слайда:
Домашнее задание: написать процедуру рисования пропеллера со стороной 40 шагов
40
Тема урока: исследование окружности в ЛОГО
Описание слайда:
Итог
Рефлексия 1
Рефлексия 2
Тема урока: исследование окружности в ЛОГО
Описание слайда:
Рефлексия 1
Тема урока: исследование окружности в ЛОГО
Сегодня я узнал(а)
Было интересно
Я понял(а), что
Я научился(ась)
У меня получилось
Меня удивило
Мне захотелось
Описание слайда:
Тема урока: исследование окружности в ЛОГО
Рефлексия 2
Формула длины окружности
Отношение длины окружности к ее диаметру
Описание слайда:
Мочалова М.В. учитель информатики лицея 144 г.Санкт-Петербург
Фомина И.О. учитель математики лицея 144 г.Санкт-Петербург
Интегрированный урок «Информатика+математика»
Тема урока «Исследование окружности в среде ЛОГО» (6 класс)
Список источников информации:
— Белова Г.В. Программирование в среде ЛОГО. М. Салон-Пресс 2006
— Макарова Н.В. Информатика и ИКТ 5-6. Питер 2008
— http://ru.wikipedia.org
— http://www.int-edu.ru/logo
Выбранный для просмотра документ Mochalova_yrok.doc
Тема урока: «Исследование окружности в среде Лого».
Предмет: Информатика + математика.
Ключевые слова : интегрированный урок, информатика + математика, 6 класс, конспект, презентация.
- Белова Г.В. Программирование в среде ЛОГО. М. Салон-Пресс 2006
- Макарова Н.В. Информатика и ИКТ 5-6. Питер 2008
- http://ru.wikipedia.org
- http://www.int-edu.ru/logo
Тип урока: урок-исследование.
Интегрированный урок: «Информатика + математика».
· Повторить темы «Правильные многоугольники в среде ЛОГО», «Окружности в среде ЛОГО».
· Путем исследования выявить закономерность между длиной окружности и ее диаметром.
· Научиться вычислять диаметр по величине окружности, т.е. по длине пути Черепашки.
· Сформировать навыки программирования сложных фигур, состоящих из частей окружностей и радиусов.
- Повторение пройденного материала
- Проверка ЗУН по пройденному материалу
- Постановка задачи и формулирование цели исследования
- Проведение исследования
- Формулирование вывода
- Рефлексия
- Домашнее задание
1. Повторение пройденного материала.
— что такое правильный многоугольник?
— приведите примеры правильных многоугольников;
— что такое, с вашей точки зрения, окружность?
— что для Черепашки является окружностью?
— как вычислить угол одного поворота Черепашки при построении правильного n -угольника?
— как посчитать путь, который пройдет Черепашка, рисуя окружность?
— какая окружность будет большего размера и почему?
а) повтори 18 [вп 18 пр 20] или повтори 18 [вп 20 пр 20]?
б) повтори 18 [вп 20 пр 20] или повтори 20 [вп 18 пр 18]?
2. Проверка ЗУН при построении окружностей разной величины.
Сейчас для проверки того, насколько вы овладели навыками построения правильных многоугольников и окружностей, мы проведем небольшую проверочную работу. В полученных карточках вы должны по каждому заданию сделать необходимые вычисления и вписать их. Затем вы обменяетесь попарно своими карточками и сделаете проверку работы товарища. После этого мы проанализируем ошибки, если они будут.
Итак, сформулируем ключевые моменты нашей темы. Правильным называется многоугольник, у которого все углы равны между собой и все стороны равны. При построении правильного многоугольника Черепашка совершает полный оборот, равный 360 0 .
Угол одного поворота головы Черепашки b при построении правильного n -угольника вычисляется по формуле
Окружность – это множество точек, равноудаленных от ее центра. Для Черепашки окружностью является правильный многоугольник с количеством сторон 36 и более. Длина окружности – это тот путь, который пройдет Черепашка, рисуя заданную окружность. Диаметр окружности — это отрезок, соединяющий 2 точки окружности и проходящий через ее центр. Все диаметры окружности пересекаются в одной точке – ее центре.
— Помнить каждому нужно,
— Что такое окружность.
— Это множество точек,
— На одном расстоянии,
— От одной только точки.
— Помни смысл этой строчки.
— Эта общая точка, по-дружески,
— Называется центром окружности.
3. Постановка задачи и формулирование цели исследования.
Предположим, мы с вами хотим попросить Черепашку нарисовать серую мышку, приведенную на рисунке. Тело мышки состоит из половинки окружности и прямой линии, которая образует замкнутую область.
Каков будет алгоритм создания тела такой мышки? (Нужно продумать, из какой точки лучше начать рисование. Давайте начнем из той точки, откуда «растет» хвостик) Сначала нужно нарисовать половину окружности с поворотом Черепашки против часовой стрелки, затем повернуть голову Черепашки на 90 0 налево и провести прямую линию до начальной точки, из которой начинали рисование. Когда тело мышки нарисовано, нужно его закрасить. В каком случае серая краска зальет весь экран? (Если прямая линия не дойдет хотя бы на один черепаший шаг до начальной точки и образуется разрыв, в который краска «вытечет»). Как исключить такую ситуацию? (Нужно нарисовать прямую линию, которая бы замкнула фигуру, т.е. нужно правильно рассчитать расстояние между двумя концами половины окружности, а это и есть диаметр окружности).
Вывод: мы должны научиться вычислять диаметр окружности, величину (длину) которой мы знаем.
4. Проведение исследования.
Для того чтобы решить поставленную задачу, мы проведем небольшое исследование.
В полученных вами карточках представлены 6 вариантов различных по величине окружностей. Во втором столбце для каждой окружности напишите формулы их построения, затем рассчитайте и впишите в 3-й столбик для каждой окружности ее длину L , т.е. тот путь, который пройдет Черепашка, рисуя окружность.
360- угольник со стор. 1
18 0- угольник со стор. 1
12 0- угольник со стор. 2
360- угольник со стор. 2
120 — угольник со стор. 4
9 0- угольник со стор. 3
На компьютере в среде ЛогоМиры создайте 6 процедур, рисующих данные окружности (не забывайте, что вы умеете копировать, работать нужно рационально). Для каждой окружности экспериментальным путем выясните ее диаметр. Для того, чтобы нарисовать именно диаметр, Черепашке нужно, нарисовав окружность, повернуть голову на 90 0 в направлении центра и пройти расстояние до противоположной части окружности с опущенным пером. Чтобы точно определить, достигла ли Черепашка противоположной стороны, ее нужно сделать невидимой, чтобы она собою не заслоняла рисуемую линию.
Полученные значения диаметров запишите в таблицу в столбик 4.
После заполнения таблицы сверните ЛогоМиры.
Дальше нам нужно рассчитать отношение длины окружности к ее диаметру. Для вычислений воспользуемся Калькулятором, встроенным в Стандартные Программы Windows . Зайдите Пуск–Программы-Стандартные-Калькулятор. Для каждого случая рассчитайте отношение L / d и запишите результат в последний столбец таблицы. Закройте Калькулятор.
5. Формулирование вывода.
Что вы заметили? Какую гипотезу вы можете сформулировать в результате проведенного исследования? Можно сделать вывод: отношение длины окружности к ее диаметру есть величина одинаковая, она называется постоянной величиной p (пи). Эта величина позволяет вычислять как величину диаметра (и радиуса) окружности по известной длине, так и наоборот: длину окружности по заданному диаметру.
Вспомните, что на занятиях наглядной геометрией в 5-ом классе, мы с вами уже проводили похожий эксперимент (измеряли длину окружности с помощью нити, вычисляли диаметр и их отношение). Сейчас вы смогли с помощью новейших компьютерных технологий повторить подобное исследование на более высоком уровне и убедиться в правильности выдвинутой гипотезы.
А сейчас немного истории. Откуда же взялось число π и почему так называется?
Самое раннее из известных приближений числа π датируется 1900 годом до н.э.
Впервые обозначением этого числа греческой буквой воспользовался британский математик Джонс в 1706 году, а общепринятым оно стало после работ Леонарда Эйлера в 1737 году.
Обозначение происходит от начальной буквы греческих слов
- окружность, периферия
- периметр.
Существует неофициальный праздник «Международный день числа π ». Он отмечается 14 марта, который в американском формате дат (месяц/день) записывается как 3.14. Примечательно, что этот праздник, случайно или умышленно, совпадает с днём рождения выдающегося физика современности Альберта Эйнштейна.
Теперь полученные знания позволят нам построить в Лого практически любые фигуры, состоящие из частей окружностей, замкнуть их и закрасить. Например, нашу мышку.
Разверните ЛогоМиры, создайте процедуру, которая позволит Черепашке нарисовать нашу мышку, не забудьте про закраску. Величину фигуры можно сделать любой по вашему желанию.
Подведем итог сегодняшнего урока:
— диаметр окружности – это отрезок, соединяющий 2 точки окружности и проходящий через ее центр;
— радиус окружности – это отрезок, соединяющий любую точку окружности с ее центром;
— радиус окружности равен половине диаметра;
— отношение длины окружности к ее диаметру есть величина постоянная, обозначается знаком p и равна 3,14.
1. Продолжите предложения:
— Сегодня я узнал (а):
— У меня получилось:
2. Формула длины окружности:
3. Отношение длины окружности к ее диаметру:
7. Домашнее задание .
Написать в тетради процедуру рисования пропеллера.
Выбранный для просмотра документ ‚ ¦®!.txt
Данный материал был скачан с сайта www . metod — kopilka . ru
. Орфография и форматирование автора материала.
Образовательно-информационный ресурс для учителей информатики,
учащихся и всех-всех, кто интересуется ИТ:
http :// www . metod — kopilka . ru Методическая копилка учителя информатики
Организационные, методические и нормативные документы,
лабораторно-практические работы (комплекс занятий по MS Word , MS Excel ,
MS Access, MS PowerPaint, Paint, Move Maker и др. прикладным программам),
лекции,конспекты, дидактический материал, занимательная информатика,
экзамен, проектная деятельность, презентации.
Все в свободном доступе! Без регистрации!
P . S . Единственным источником дохода сайта является переход по рекламным ссылкам.
Если ресурс оказался Вам полезен, потратьте 1 минуту времени и кликните любой рекламный блок на сайте.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
http://urok.1sept.ru/articles/632635
http://infourok.ru/integrirovannyj-urok-informatika-matematika-issledovanie-okruzhnosti-v-srede-logo-6-klass-4915246.html
На уроке рассмотрен материал для подготовки к ОГЭ (ГИА) по информатике, разбор 8 задания. Объясняется тема об осуществлении поиска информации в Интернете, логических выражениях и запросах.
Содержание:
- ОГЭ по информатике 8 задания объяснение
- 8 задание как решать
- Актуальное
- Тренировочные
8-е задание: «Поиск информации в Интернете»
Уровень сложности — повышенный,
Максимальный балл — 1,
Примерное время выполнения — 5 минут.
* до 2020 г — это было задание № 18 ОГЭ
- Поисковые запросы:
-
- операция «И» (
&) в поисковом запросе всегда ограничивает поиск (уменьшает количество страниц в выдаче), т. е., в ответ на запрос яблоко И груша поисковый сервер выдаст меньше страниц, чем на запрос яблоко, потому что будет искать страницы, на которых присутствуют оба этих слова;
- операция «И» (
чем больше в запросе операций «И», тем меньше результатов
-
- операция «ИЛИ» (
|) в поисковом запросе всегда расширяет поиск (увеличивает количество страниц в выдаче), т. е., в ответ на запрос яблоко ИЛИ груша поисковик выдаст больше страниц, чем на запрос яблоко, потому что будет искать страницы, на которых присутствует хотя бы одно из этих слов (или сразу оба слова).
- операция «ИЛИ» (
чем больше в запросе «ИЛИ», тем больше результатов
- Круги Эйлера-Вена:
Решать 8 задание также можно, представляя запрос в виде кругов Эйлера-Вена:
- Операция «И» представляется как умножение (пересечение).
- Операция «ИЛИ» представляется как сложение (объединение).
- Заштрихованная область при объединении больше, чем при пересечении.
Пример использования кругов Эйлера:
Пример:
Известно количество сайтов, которых находит поисковый сервер по следующим запросам :
| Ключевое слово | Количество сайтов, для которых данное слово является ключевым |
|---|---|
| Глинка & Лист | 320 |
| Бах & Лист | 280 |
| (Глинка | Бах) & Лист | 430 |
Сколько сайтов будет найдено по запросу
Глинка & Бах & Лист
- Упрощение логических выражений:
(A & B) | C = (A | C) & (B | C)
(A | B) & C = (A & C) | (B & C)
8 задание как решать
Актуальное
Разбор задания 8.1: Демонстрационный вариант ОГЭ 2022 г.:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Какое количество страниц (в тысячах) будет найдено по запросу Рыбка?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Рыбак | Рыбка | 780 |
| Рыбак | 260 |
| Рыбак & Рыбка | 50 |
✍ Решение:
-
✎ Решим задание с помощью кругов Эйлера-Вена.
- Сначала отобразим первую строку таблицы — т.е. операцию
ИЛИ(|), которая обозначает объединение одновременно двух кругов: - Для второй строки таблицы отобразим отдельный круг, соответствующий количеству страниц для слова
Рыбак: - В третьей строке наблюдаем операцию И (
&), что соответствует области пересечения кругов: - Поскольку в задании требуется найти запрос
Рыбка, то для начала нам необходимо из общего объединения, т.е. из первого изображения, «вычесть» результат второго изображения, т.е.Рыбак; получим: - Теперь, чтобы получить полностью число страниц для запроса
Рыбка, необходимо добавить область пересечения кругов, которая равна 50 (вычисление для третьей строки); т.е. получим:
520 + 50 = 570
Ответ: 570
Тренировочные
Разбор задания 8.2:
В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код — соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые нашёл поисковый сервер по каждому запросу. По всем запросам было найдено разное количество страниц.
Для обозначения логической операции «ИЛИ» в запросе используется символ «|», а для логической операции «И» — «&»:
| Код | Запрос |
|---|---|
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
✍ Решение:
✎
Способ 1:
(Муха & Денежка) | Самовар = (Муха | Самовар) & (Денежка | Самовар)
Ответ: ВАГБ
✎ Способ 2:
- Для начала отобразим все 4 объекта задания в виде пересеченных кругов одинакового размера:
- Рассмотрим строку с кодом А. Сначала необходимо выполнить действие в скобках: (Муха & Денежка). Логическое «И» представляется, как область пересечения двух кругов:
- Теперь выполним операцию «ИЛИ» — результат пересечения | Самовар. Для этого нам необходимо к полученной области «добавить» круг для объекта Самовар:
- Таким образом, мы получили область для кода А.
- Рассмотрим строку для кода Б: операция «И» — Муха & Денежка & Базар & Самовар — обозначает область пересечения одновременно всех кругов:
- Рассмотрим строку для кода Б:
- Рассмотрим строку для кода В: операция «ИЛИ» — Муха | Денежка | Самовар — обозначает объединение одновременно всех трех кругов:
- Рассмотрим строку для кода Г: операция «И» — Муха & Денежка & Самовар — обозначает область пересечения одновременно всех трех кругов:
- То есть выделенная область одновременно принадлежит и кругу Муха, и кругу Денежка, и кругу Самовар.
- Сравним все четыре полученных области и расположим их в порядке убывания, то есть с самой большой области до самой маленькой: ВАГБ
Решим задание с помощью кругов Эйлера-Вена.
Ответ: ВАГБ
Разбор задания 8.3:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Пьер & Наука | 180 |
| Пьер & (Наука | Кюри) | 410 |
| Пьер & Кюри | 320 |
Какое количество страниц (в тысячах) будет найдено по запросу:
Пьер & Наука & Кюри
✍ Решение:
- Везде присутствует сомножитель «Пьер &» (и в искомом запросе!), сократим его:
- Используем круги Эйлера для решения, обозначив цифрами каждую составляющую:
- Из схемы и исходных данных получим:
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Наука | 180 |
| Наука | Кюри | 410 |
| Кюри | 320 |
Искомый запрос: Наука & Кюри
1. №1 + №2 = 180 (Наука) 2. №2 + №3 = 320 (Кюри) 3. №1 + №2 + №3 = 410 (Наука | Кюри)
№1 + №2 + №3 = 180 + №3 = 410 №3 = 410 - 180 = 230
№2 + №3 = №2 + 230 = 320 №2 = 320 - 230 = 90
Результат: 90
Содержание
- Как найти человека в ВК
- – По фото
- – По фамилии
- – По номеру телефона
- – По геолокации
- – По ID
- – По кругу общения (через друзей)
- – По дате рождения и другим данным
- – По сообществам
- Как найти человека в ВК без регистрации
- – Через поисковые системы
- – Через телеграм каналы
- – Через сервис VK.BARKOV.NET
- FAQ
- – Можно ли найти человека по айпи адресу?
- – Можно ли найти человека по статусу в ВК?
- – Как в ВК найти заблокированных людей?
- – Как найти вторую страницу человека в ВК?
Социальная сеть ВКонтакте охватывает 84% аудитории рунета. В месяц сюда заходят около 73,4 млн российских пользователей. Это огромная база людей, в которой можно найти знакомых, коллег по работе, родственников и одноклассников.
Но если не знать адрес страницы человека, найти его может быть сложно. Особенно если он скрыл информацию профиля и зарегистрировался не под настоящей фамилией. В этой статье разберем все возможные способы поиска людей ВК, от простых до не самых очевидных.
Как найти человека в ВК
ВКонтакте пользователи оставляют на странице очень много личной информации. Например, место учебы и работы, родной город, музыкальные предпочтения, интересы и даже номер телефона. Зная хотя бы базовую информацию, будет проще найти человека.
Сначала рассмотрим способы поиска людей непосредственно ВКонтакте.
По фото
Если у вас есть фотография человека, самый простой вариант найти его страницу ВК — использовать поиск по изображению.
👉 Чтобы найти человека по фото:
1 Откройте Яндекс.Картинки;
2 Добавьте фото в поисковую строку и нажмите «найти«;
3 Если фото связано с профилем ВК, вы увидите активные ссылки на страницу в соц. сети.
Снимки пользователя можно найти в других его социальных сетях и мессенджерах. Например, иногда люди ставят одно и то же фото на аву ВК и Телеграм. Поисковая система найдет снимок, даже если его установили не как главное фото профиля, а добавили на стену или в альбом.
💭 Помните, что фото человека может использовать кто угодно. Поэтому не удивляйтесь, если найдете несколько разных страниц с одним и тем же изображением. Вам придется самостоятельно определить, кто перед вами, фейк человека которого вы ищите, или его реальный аккаунт.
По фамилии
На первый взгляд самый очевидный вариант поиска — поиск по имени и фамилии. Но здесь могут возникнуть сложности, если:
- Человек указал в аккаунте ненастоящие имя и фамилию;
- Вам известен только псевдоним;
- Имя и фамилия не редкие, и в ВК тысячи аккаунтов по этому запросу.
👉 Чтобы найти профиль ВК по фамилии:
1 Зайдите ВК;
2 Нажмите на кнопку «лупа» в правом верхнем углу над новостной лентой (для мобильных устройств), или кликните по поисковой строке в верхней части экрана (для ПК версии);
3 Вбейте в поисковую строку имя и фамилию и нажмите «Enter» (или «Найти»).
В первую очередь ВК выдаст тех, с кем у вас есть общие друзья, с кем вы общались или обменивались комментарии. При этом они могут полностью не отвечать запросу, совпасть только по фамилии или имени. Ниже отобразятся все пользователи с заданным именем и фамилией.
По номеру телефона
Если вам известен номер телефона человека, найти его ВКонтакте не составит труда. Но только при условии, что именно на этот номер он зарегистрировал свою страницу.
Вариант #1: Для начала вбейте этот номер в поисковик. Если человек указал номер на своей странице, поисковик выдаст ссылку на нее.
Вариант #2: Можно найти человека в ВК по номеру телефона, если его номер есть в вашей телефонной книге.
Сначала нужно синхронизировать контакты:
1 Откройте мобильное приложение ВК и войдите в «Настройки«;
2 Выберите «Приложение«;
3 В разделе «Контакты» выберите «Синхронизировать контакты«;
4 Разрешите ВК доступ к списку контактов.
После этого:
1 Откройте список друзей;
2 Нажмите на кнопку «Добавить друга«;
3 Выберите «Импорт телефонной книги«.
После этого вы увидите все аккаунты, связанные с номерами в вашей телефонной книге. Останется найти среди них нужного человека.
По геолокации
Вариант #1: найти людей поблизости можно с помощью мини-приложения «Люди рядом». Оно абсолютно легальное и поддерживается ВКонтакте.
👉 Чтобы найти людей рядом:
1 Откройте приложение «Люди рядом» на ПК или в мобильном приложении;
2 Приложение запросит у вас доступ к вашей геопозиции и расскажет о том, как работает поиск, вам нужно дать ему разрешение и нажать «Продолжить«;
3 После вы увидите список людей, которые находятся рядом с вами. При этом приложение укажет, на каком расстоянии от вас они находятся.
Проблема в том, что приложение покажет только тех, кто дал разрешение на доступ к своей геопозиции. Шанс, что здесь окажется нужный вам человек, очень мал. Но попробовать стоит.
Вариант #2: еще один вариант поиска по местоположению — поиск фотографий с геолокацией. Проще всего это сделать через ПК версию.
1 Откройте любое свое фото, на котором отмечено местоположение;
2 Нажмите на геолокацию;
3 Откроется карта и галерея снимков «Фотографии рядом«;
4 Если вы ищите человека по другой локации, нажмите на значок «Лупа» в правом верхнем углу над картой;
5 Откроется новая карта, поставьте точку в любом интересующем вас месте (городе, поселке и т.п.) и нажмите «Сохранить местоположение«.
Изменится геометка на вашем фото. Снова нажмите на нее, и вы увидите снимки, сделанные в этом же месте. Этот способ подходит для поиска людей в конкретных микрорайонах и небольших населенных пунктах. Просто просматривайте фото и страницы их авторов, и высока вероятность, что вы найдете нужного человека.
По ID
ID — это уникальный идентификатор пользователя. Он отображается в верхней строке браузера.
По умолчанию ID состоит из цифр, выданных пользователю случайным образом. Но многие люди меняют его, например, заменяют цифры никнеймом или своими инициалами.
Очень часто в качестве ID устанавливают никнейм из других соц. сетей. Если вам известен ник человека в другой соц. сети, можно попробовать найти его по нему ВК. Для этого в строку браузера вставьте предполагаемый ID:
https://vk.com/[ник]
Вот несколько вариантов для ника «Toy Story»:
- https://vk.com/toystory
- https://vk.com/toy_story
- https://vk.com/toystory_
- https://vk.com/toy__story
По кругу общения (через друзей)
Соц. сеть ВКонтакте создает для каждого пользователя индивидуальные подборки рекомендованных друзей. Алгоритм подбирает пользователей по нескольким критериям:
- Наличие общих друзей;
- Наличие их номера в ваших мессенджерах и телефонной книге (если вы открыли ВК доступ к телефонной книге);
- Обучение в одном и том же вузе;
- Работа в одной и той же компании;
- Подписки на схожие сообщества.
Учитываются все критерии сразу, таким образом ВК и формирует список предполагаемых друзей.
👉 Чтобы открыть рекомендации, зайдите в список друзей и нажмите «Добавить друга«.
Если у вас есть общие друзья с человеком, которого вы ищите, найти его можно и через них. Откройте список друзей общего знакомого, попробуйте найти там нужного человека. Если друзей очень много, просмотрите лайки и комментарии на странице. Возможно именно там отметился нужный вам человек.
По дате рождения и другим данным
В случае, если ни один из вышеупомянутых способов не помог, можно попробовать найти человека по личной информации.
ВК доступен поиск по:
- Дате рождения;
- Школе и университету (с годом выпуска);
- Полу и возрасту;
- Семейному положению;
- Жизненной позиции;
- Месту работы и должности;
- Военной службе;
- Стране и городу проживания.
Зная эту информацию можно существенно сузить круг поиска, особенно в случае, когда вам известны только имя и фамилия, но пользователей с такими данными слишком много. Найти человека вы сможете только при соблюдении двух условий: он указал эту информацию в своем профиле, его профиль открыт.
👉 Чтобы найти пользователя по известным вам данным о нем:
1 Откройте список друзей;
2 Выберите «Поиск друзей» и заполните информацию в поле «Параметры поиска«.
По сообществам
Поиск по локальным группам может дать хороший результат.
Предположим, что вы ищите человека, который живет (или жил) в районе Ивановское ВАО. В таком случае:
1 Найдите несколько сообществ ВК этого района;
2 Откройте список подписчиков сообщества;
3 Попробуйте найти в этом списке нужного человека. Чтобы сузить поиск, можно попробовать ввести имя, фамилию, примерный возраст.
Искать можно по хобби, интересам, образу жизни. Попробуйте найти страницу человека в группе его педагога по танцам или тату-мастера.
Как найти человека в ВК без регистрации
Поиск людей ВКонтакте возможен и без регистрации в приложении.
Через поисковые системы
Откройте Яндекс или Гугл и вбейте в поисковую строку ту информацию, что вам известна о пользователе.
💁♀️ Например, если вы знаете ник пользователя в другой соц. сети, запрос лучше сформулировать так:
ник + ВК
или
имя и фамилия + ВК
При поиске специалистов можно добавлять название профессии или место работы. Подойдет любая известная вам информация.
Например:
Иван Иванов + юрист + ВК
Через телеграм каналы
В Телеграм много каналов и ботов по поиску людей, например, «Глаз Бога», «Колибри Осинт», «ГНАйе Бот». Проблема в том, что многие из них регулярно блокируются, а некоторые предлагают платную помощь, но не оказывают ее.
⚠️ Помните, что в интернете очень много мошенников. Не платите деньги администраторам Телеграм-каналов, о которых вы ничего не знаете. Для начала почитайте отзывы о канале или найдите пару обзоров на них в интернете.
Через сервис VK.BARKOV.NET
В сервисе VK.BARKOV.NET есть много скриптов для поиска людей ВКонтакте.
Здесь можно найти человека:
- По геолокации;
- По тексту в статусе;
- По сайту, указанному в профиле;
- По дню рождения его партнера;
- По его детям или родителям.
- По интересам (любимой музыке, кино, книгам);
- По мобильному приложению, через которое он входит ВКонтакте;
Многих этих функций поиска нет внутри самой социальной сети. Вам нужно будет выбрать подходящий скрипт, заполнить данные для поиска и запустить сбор аккаунтов. Сервис соберет вам все профили, подходящие под ваш запрос.
Сервис платный. Полный доступ ко всем скриптам стоит 799 рублей в месяц. Для разовых задач есть тариф на 24 часа за 299 рублей.
FAQ
Можно ли найти человека по айпи адресу?
Вычислить точный адрес по IP очень сложно. В реальности этим занимаются только правоохранительные органы.
Можно ли найти человека по статусу в ВК?
Раньше в ВК была функция поиска по словам в статусе. Сегодня она не работает. Но поиск по статусу ВК есть у сторонних сервисов, например у VK.BARKOV.NET и ЦереброТаргет.
Как в ВК найти заблокированных людей?
Если пользователя заблокировали, вся информация на его странице будет недоступна, поэтому искать ее нет смысла.
Как найти вторую страницу человека в ВК?
Если человек создал копию своей страницы, найти ее можно будет по фото или имени и фамилии. Если же вторая страница создана под фейковыми данными, найти ее практически невозможно.
Но вы можете настроить синхронизацию контактов для ВК. В таком случае, когда человек, чей номер есть в вашем списке контактов, зарегистрирует новую страницу и привяжет ее к этому номеру, ВК пришлет вам уведомление со ссылкой на вторую страницу.
Способов поиска людей ВКонтакте очень много. Все зависит от того, сколько у вас данных о конкретном человеке. Проще всего найти пользователя, зная его номер телефона и ID страницы. Эффективно работает поиск по фото. В остальных случаях нужно запастись терпением и воспользоваться поиском по другим данным, например, по месту работы и интересам.
Нередко возникает необходимость найти страницу по номеру телефона в ВК, будь то старый знакомый, одноклассник или дальний родственник. А если этот человек пользуется соц.сетью с фейкового аккаунта, то телефон и вовсе остаётся единственной зацепкой. Несмотря на то, что поиск по номеру может быть весьма проблематичным, в некоторых ситуациях он помогает даже если человек давно не пользуется SIM-картой, по которой вы его ищите. Но обо всём по порядку.
Поиск страницы по номеру ВК: можно ли
Руководство ВКонтакте на протяжении последних лет систематически усложняет способы узнать страницу пользователя по номеру мобильного, к которому она привязана. В качестве примера вышеупомянутых мер можно вспомнить поиск пользователя через функцию восстановления пароля. Изначально можно было получить ссылку на страницу, потом осталось лишь фото, а теперь нет и его. Вероятно, многие из вас вспомнят ещё парочку неактуальных нынче способов, ну а в этой статье мы разберём несколько тех, что до сих пор работают и (скорее всего) так и продолжат существовать в 2022 .
Способ №1: через поиск ВКонтакте
Самое банальное – это ввести номер мобильного в строку поиска ВКонтакте. Если номер указан на странице, то вы почти наверняка сможете найти нужного человека.
- Вводите номер телефона в адресную строку.
- Нажимаете клавишу Enter.
- Открываете вкладку Люди.

Если нужная страница не отобразилась в результатах поиска, то переходим к следующему способу.
Способ №2: через поисковую систему
Внутренний поиск ВКонтакте индексирует далеко не всё содержание страниц, поэтому есть вариант воспользоваться сторонними поисковыми системами – Google, Яндекс или другими.
- Открыв главную страницу, введите в поисковую строку следующее.
- site:vk.com «Номер телефона»(без кавычек). Такой запрос позволит отсеять все результаты, которые находятся за пределами ВКонтакте.
- Если запрашиваемый номер не скрыт, поисковая система выдаст нужную страничку одной из первых.
К сожалению, это способ тоже не идеален, поскольку некоторые страницы ВКонтакте защищены от индексирования поисковыми системами посредством соответствующих настроек приватности.
Способ №3: через синхронизацию контактов
Вам потребуется Андроид-смартфон с установленным официальным приложением ВКонтакте.
- Внесите нужный номер в телефонную книгу (имя можно указывать любое).
- Запустите приложение ВКонтакте.
- Откройте настройки и зайдите в раздел Учётная запись.
- Прочее – Синхронизация контактов.
- Выберите пункт Только контакты.
- Зайдите в меню «Мои Друзья».
- Кликните по «+» или «Добавить» и выберите импорт по контактам.
Далее соц.сеть покажет вам странички, которые зарегистрированы на добавленные в телефонную книгу номера.

Способ №4: при помощи телефона с пустым списком контактов
Крайний случай. Если вам срочно нужно найти человека по номеру телефона, то вы можете воспользоваться данным способом, он похож на предыдущий, но из-за того что синхронизация будет ограничена одним номером, она пройдет быстрее и нужный контакт не потеряется среди десятков других в возможных друзьях.
- Очищаете телефонную книгу на смартфоне (для удобства можно забекапить контакты в облако).
- Вносите требуемый номер телефона в контакты.
- Повторяете пункты 2-7 из предыдущего списка.
Как уже говорилось, через ВКонтакте можно найти даже того человека, который давно не пользуется своим старым телефоном. Дело в том, что далеко не все меняют в номер страницы ВК, а приобретая новую SIM-карту оставляют в ВК телефон, которым уже не пользуются.
Поиск страницы ВКонтакте по номеру телефона – это относительно просто, однако здесь многое зависит от настроек приватности, которые установил нужный вам человек. На 2022 год это единственные актуальные способы поиска онлайн, как вариант вы можете повторить то же самое в Фейсбуке, возможно пользователь забыл скрыть свой номер там.