Зная ребро в основании треугольной призмы, можно сразу вычислить высоту основания, его площадь и радиусы вписанной и описанной окружностей в равносторонний треугольник, выполняющий роль основания, по стандартным формулам для правильных многоугольников.
h=a/√2
r=a/(2√3)
R=a/√3
S=(√3 a^2)/4
Затем, используя диагональ боковой грани, можно вычислить боковое ребро через сторону основания по теореме Пифагора в получившемся прямоугольном треугольнике, и найти периметр треугольной призмы, который состоит из суммы всех ее боковых ребер и сторон основания.
b=√(d^2-a^2 )
P=3(2a+b)=3(2a+√(d^2-a^2 ))
Площадь боковой поверхности треугольной призмы представляет собой три площади прямоугольников, являющихся боковыми гранями, со сторонами a и b. Чтобы найти площадь полной поверхности, нужно сложить площадь боковой поверхности треугольной призмы с двумя площадями оснований.
S_(б.п.)=3ab=3a√(d^2-a^2 )
S_(п.п.)=3a√(d^2-a^2 )+(√3 a^2)/4
Чтобы вычислить объем треугольной призмы, нужно умножить площадь равностороннего треугольника, находящегося в ее основании, на боковое ребро, которое по совместительству является высотой призмы.
V=(√(3(d^2-a^2 ) ) a^2)/4
Радиус вписанной в треугольную призму сферы равен радиусу окружности, вписанной в основание, но такая сфера существует, только если высота треугольной призмы, то есть ее боковое ребро, равна диаметру указанной окружности. Радиус сферы, описанной вокруг треугольной призмы, равен по значению стороне основанию призмы, умноженной на корень из 5/6.
r_1=r
R_1=√(5/6) a
Советы к решению задач на призму
1. Если в условии задачи говорится диагональ боковой грани прямой призмы, то помните, что:
— Проекцией этой диагонали на плоскость основания будет соответствующая сторона основы призмы. Диагональ боковой грани прямой призмы, соответствующая ей сторона основания и боковое ребро призмы выходит с конца диагонали, образуют прямоугольный треугольник;
— Углом наклона диагонали боковой грани к плоскости основания будет угол между этой диагональю и соответствующей стороной основы призмы;
Если заданы или найдены диагональ боковой грани призмы и угол ее наклона к плоскости основания, или это диагональ и соответствующая ей сторона основы, то можно найти высоту призмы с помощью тригонометрических соотношений в прямоугольном треугольнике или последствий теоремы Пифагора.
2. Если в условии задачи говорится диагональ прямой призмы, то помните, что:
— Проекцией этой диагонали на плоскость основы будет соответствующая ей диагональ основания призмы. При этом большей диагонали основы соответствует большая диагональ призмы, меньшей — меньше диагональ призмы. Диагональ прямой призмы, соответствующая ей диагональ основания и боковое ребро призмы выходит с конца диагонали, образуют прямоугольный треугольник;
— Углом наклона диагонали прямой призмы к плоскости основания будет угол между этой диагональю и соответствующей диагональю основания призмы;
Если заданы или найдены диагональ прямой призмы и угол ее наклона к плоскости основания, или это диагональ и соответствующая ей диагональ основания основы, то можно найти высоту призмы с помощью тригонометрических соотношений в прямоугольном треугольнике или последствий теоремы Пифагора.
3. Если в условии задачи говорится сечение прямой призмы плоскостью, то помните, что:
— Если секущая плоскость проходит, например, через сторону основания прямой треугольной призмы и противоположную ей вершину призмы, принадлежащего другой основе, то сечением будет треугольник, ортогональной проекцией которого на плоскость основы будет треугольник, лежащий в основе призмы. Если известна площадь такого сечения и угол наклона плоскости сечения к плоскости основания, то можно найти площадь основания призмы. Площадь основания в таком случае будет равна площади сечения, помноженной на косинус угла между плоскостями сечения и основания. Соответственно площадь такого сечения будет равна площади основания, деленной на косинус угла между плоскостями сечения и основания.
Чтобы найти угол между плоскостью сечения и плоскостью основания, надо в одной из этих плоскостей провести перпендикуляр к общей прямой плоскостей и из основания перпендикуляра, во второй плоскости провести перпендикуляр к общей прямой плоскостей.
В случае правильной треугольной призмы угол наклона плоскости сечения, проходящей через сторону основания прямой треугольной призмы и противоположную ей вершину призмы к плоскости основания, будет угол между соответствующими высотами сечения и основы призмы.
Правильная четырехугольная призма
Определение.
Правильная четырехугольная призма — это шестигранник, основаниями которого являются два равных квадрата, а боковые грани представляют собой равные прямоугольники
Боковое ребро — это общая сторона двух смежных боковых граней
Высота призмы — это отрезок, перпендикулярный основаниям призмы
Диагональ призмы — отрезок, соединяющий две вершины оснований, которые не принадлежат к одной грани
Диагональная плоскость — плоскость, которая проходит через диагональ призмы и ее боковые ребра
Диагональное сечение — границы пересечения призмы и диагональной плоскости. Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
Перпендикулярное сечение (ортогональное сечение) — это пересечение призмы и плоскости, проведенной перпендикулярно ее боковым ребрам
Элементы правильной четырехугольной призмы
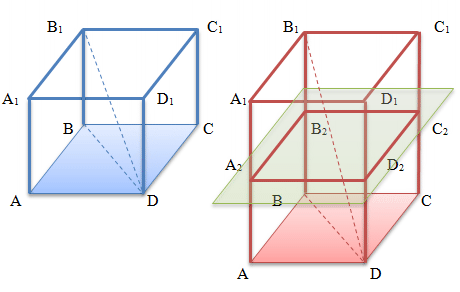
На рисунке изображены две правильные четырехугольные призмы, у которых обозначены соответствующими буквами:
- Основания ABCD и A1B1C1D1 равны и параллельны друг другу
- Боковые грани AA1D1D, AA1B1B, BB1C1C и CC1D1D, каждая из которых является прямоугольником
- Боковая поверхность — сумма площадей всех боковых граней призмы
- Полная поверхность — сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
- Боковые ребра AA1, BB1, CC1 и DD1.
- Диагональ B1D
- Диагональ основания BD
- Диагональное сечение BB1D1D
- Перпендикулярное сечение A2B2C2D2 .
Свойства правильной четырехугольной призмы
- Основаниями являются два равных квадрата
- Основания параллельны друг другу
- Боковыми гранями являются прямоугольники
- Боковые грани равны между собой
- Боковые грани перпендикулярны основаниям
- Боковые ребра параллельны между собой и равны
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
- Углы перпендикулярного сечения — прямые
- Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
- Перпендикулярное (ортогональное сечение) параллельно основаниям
Формулы для правильной четырехугольной призмы
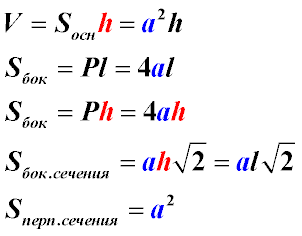
Указания к решению задач
При решении задач на тему «правильная четырехугольная призма» подразумевается, что:
Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия — призма). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ .
Задача.
В правильной четырёхугольной призме площадь основания 144 см2, а высота 14 см. Найти диагональ призмы и площадь полной поверхности.
Решение.
Правильный четырехугольник — это квадрат.
Соответственно, сторона основания будет равна
√144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 122 + 122 ) = √288 = 12√2
Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 )2 + 142 ) = 22 см
Ответ: 22 см
Задача
Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.
Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:
a2 + a2 = 52
2a2 = 25
a = √12,5
Высота боковой грани (обозначим как h) тогда будет равна:
h2 + 12,5 = 42
h2 + 12,5 = 16
h2 = 3,5
h = √3,5
Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания
S = 2a2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см2 .
Ответ: 25 + 10√7 ≈ 51,46 см2 .
15306.1214
Прямая призма |
Описание курса
| Куб
Призма
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.
Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
$С_1Н$ — высота
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
Чтобы были понятны формулы, введем обозначения:
$P_{осн}$ — периметр основания;
$S_{осн}$ — площадь основания;
$S_{бок}$ — площадь боковой поверхности;
$S_{п.п}$ — площадь полной поверхности;
$h$ — высота призмы.
$S_{бок}=P_{осн}·h$
$S_{п.п}=S_{бок}+2S_{осн}$
$V=S_{осн}·h$
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
В основании лежит четырехугольник
1. Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
1. Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны.
2. Квадрат
$S=a^2$, где $а$ — сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
$S=6·S_{треугольника}={6·a^2√3}/{4}={3·a^2√3}/{2}$, где $а$ — сторона правильного шестиугольника.
Пример:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.
Решение:
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
$S_{п.п}=S_{бок}+2S_{осн}=P_{осн}·h+2S_{ромба}$
В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.
$АВ=√{5^2+12^2}=√{25+144}=√{169}=13$
$Р=13·4=52$
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
$S_{основания}={d_1·d_2}/{2}={10·24}/{2}=120$
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
$S_{п.п}=P_{осн}·h+2S_{ромба}=52·20+2·120=1040+240=1280$
Ответ: $1280$
Цилиндр — это та же призма, в основании которой лежит круг.
$S_{бок}=P_{осн}·h=2πRh$
$S_{п.п}=S_{бок}+2S_{осн}=2πRh+2πR^2=2πR(h+R)$
$V=S_{осн}·h=πR^2 h$
Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.
Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
$MN {//} AC, MN = {AC}/{2}$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$AC^2+BC^2=AB^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα;$
$b^2=a^2+c^2-2·a·c·cosβ;$
$c^2=b^2+a^2-2·b·a·cosγ.$
АЛ
Андрей Лихачёв «женат»
Зная диагонали призмы и высоту призмы по теореме Пифагора находим диагонали ромба.
Зная диагонали ромба по теореме Пифагора находим сторону ромба т. е. сторону основания призмы. Если возникнут вопросы — пиши в агент.
