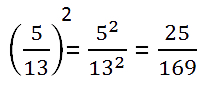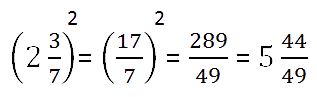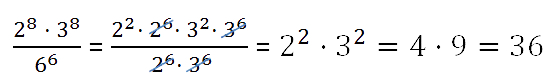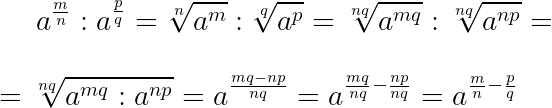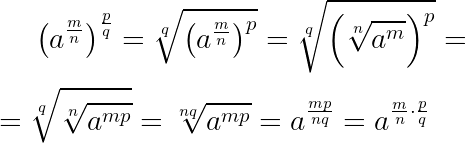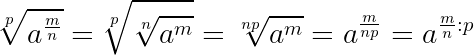Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Возведение дроби в степень
Поддержать сайт
Запомните!
При возведении в степень дроби нужно
возвести в степень и числитель, и знаменатель.
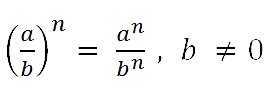
Данное свойство соответствует другой записи свойства № 5
«Степень частного», расмотренного на предыдущей странице.
Примеры возведения в степень дроби.
-
()2 =
=
=
Как возвести в степень смешанное число
Чтобы возвести в степень смешанное число, сначала избавляемся от целой
части, превращая смешанное число в неправильную дробь. После этого
возводим в степень и числитель, и знаменатель.
Пример.
Формулу возведения в степень дроби применяют как
слева направо, так и справа налево, то есть, чтобы
разделить друг на друга степени
одинаковыми показателями, можно разделить одно основание на другое,
а показатель степени оставить неизменным.
- Пример. Найти значение выражения рациональным способом.
На нашем сайте вы также можете проверить свои вычисления и
возвести число в степень онлайн.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
План урока:
Степень с рациональным показателем
Свойства дробных степеней и операции с ними
Сравнение степеней
Степень с рациональным показателем
Напомним, что в 7 классе мы впервые познакомились с понятием степени, причем тогда рассматривались случаи, когда показателем степени является натуральное число. В 8 классе понятие степени было расширено, теперь в него включались случаи, когда показатель являлся целым числом. Настоятельно рекомендуем перечитать соответствующие уроки. Сегодня же мы можем сделать ещё один шаг вперед и рассмотреть степени с рациональными показателями.
При расширении понятия степени важно обеспечить то, чтобы уже известные правила работы с целыми степенями работали и для дробных показателей. Одно из свойств степеней выглядит так:
(am)n = amn
Подставим в эту формулу следующие значения переменных:
а = 3
m = 1/6
n = 6
Мы специально выбрали эти числа такими, чтобы произведение mn равнялось единице:
mn = (1/6)•6 = 1
Подставляем эти значения:
(31/6)6 = 31/6•6 = 31 = 3
Получили, что
(31/6)6 = 3
Однако по определению корня n-ой степени число, дающее при возведении в шестую степень тройку, является корнем шестой степени из трех. То есть можно записать:
С помощью подобных преобразований нам удалось указать, чему равно число, возведенное в дробную степень. Аналогично можно показать, что для любого а > 0 справедлива формула:
Действительно, если возвести левую часть в n-ую степень, то получим:
(а1/n)n = a1/n•n = a
Значит, по определению корня n-ой степени
Ограничение а > 0 необходимо для того, чтобы не рассматривать случаи, когда подкоренное выражение является отрицательным.
Продолжим наши рассуждения. Чему будет равна степень аm/n? Ясно, что дробь m/n можно представить в виде:
m/n = (1/n)•m
C учетом этого выполним преобразование:
В результате несложных преобразований нам удалось получить формулу, позволяющую возводить число в степень, у которой рациональный показатель!
Приведем несколько примеров вычисления дробных степеней:
Часто при вычислениях удобнее сначала извлечь корень из числа, а потом полученный результат возвести в степень:
Напомним, что одну и ту же дробь можно представить разными способами, например:
1/2 = 2/4 = 3/6 = 4/8 = 5/10 = 0,5
Возникает вопрос – изменится ли значение дробной степени, если мы приведем дробь к новому знаменателю? Очевидно, что нет, но всё же убедимся в этом на примере. Сначала возведем в степень 1/2 число 25:
Теперь заменим дробь 1/2 на идентичную ей дробь 2/4:
Результат не изменился. В общем случае есть смысл максимально сократить дробь перед вычислением, чтобы избежать операций с большими числами. Особенно это касается десятичных дробей. Например, пусть необходимо вычислить значение выражения 810,25. По определению десятичной дроби можно записать, что 0,25 = 25/100. Тогда вычислить 810,25 можно так:
Согласитесь, возводить число 81 в 25-ую степень не очень легко! Поэтому поступим иначе. Сократим дробь 25/100:
0,25 = 25/100 = 25/(25•4) = 1/4
Теперь вычисления будет более простыми:
Вообще легко запомнить, что 0,25 = 1/4, а 0,5 = 1/2. Замена десятичных дробей обыкновенными дробями сильно упрощает вычисления. Приведем примеры:
Свойства дробных степеней и операции с ними
Когда мы изучали степени с целыми показателями, мы выяснили, что правила работы с ними ничем не отличаются от правил работы со степенями с натуральным показателем. Оказывается, эти же правила работают и для степеней с рациональным показателем. Сформулируем основные свойства дробных степеней.
Например, справедливы следующие действия:
50,5•52,5 = 50,5 + 2,5 = 53 = 125
195/3•191/3 = 195/3 + 1/3 = 192 = 361
29,36–0,37•29,361,37 = 29,36–0,37 + 1,37 = 29,361 = 29,36
Вот несколько примеров подобных вычислений:
174,5:173,5 = 174,5–3,5 = 171 = 1
49,36:46,36 = 49,36–6,36 = 43 = 64
2012:2014 = 2012–14 = 20–2
Проиллюстрируем это правило примерами:
(60,25)8 = 60,25•8 = 62 = 36
(93/2)2 = 9(3/2)•2 = 93 = 729
(254)0,125 = 254•0,125 = 250,5 = 5
Покажем, как можно применять данное правило:
41/6•161/6 = (4•64)1/6 = 641/6 = 2
0,51,5•501,5 = (0,5•50)1,5 = 251,5 = 251+0,5 = 251•250,5 = 25•5 = 125
4,90,5•100,5 = (4,9•10)0,5 = 490,5 =7
Это правило можно применять следующим образом:
3600,5:100,5 = (360:10)0,5 = 360,5 = 6
5003:503 = (500:50)3 = 103 = 1000
6,251/4:0,011/4 = (6,25:0,01)1/4 = 6251/4 = 5
Заметим, что степени очень удобны тем, что с их помощью легко упростить работу с корнями, ведь если
то верное и обратное:
То есть любое выражение с корнями в виде степени с рациональным показателем.
Пример. Вычислите значение выражения
Решение. Корней много, поэтому для удобства заменим их степенями
Получили тоже самое выражение, но в более компактном виде. Посчитаем его значение:
(91/4)1/5•39/10 = (90,25)0,2•30,9 = 90,25•0,2•30,9 = 90,05•30,9 = (32)0,05•30,9 =
=32•0,05•30,9 = 30,1•30,9 = 30,1•0,9 = 31 = 3
Ответ: 3.
Пример. Упростите выражение
(81n+1– 65•81n)0,25
Решение. Степень 81n+1можно представить как произведение:
81n+1 = 81n•811 = 81•81n
С учетом этого можно записать:
(81n+1– 65•81n)0,25 = (81•81n– 65•81n)0,25 = (81n(81 – 65))0,25 =
= (81n•16)0,25 = 810,25n •160,25 = 810,25n •161/4 = 2•810,25n
Ответ: 2•810,25n.
Сравнение степеней
Напомним, что из двух корней n-ой степени больше тот, у которого больше подкоренное выражение:
Отсюда следует вывод, что если a<b, то
а1/n<b1/n
теперь возведем каждую часть этого неравенства в степень m. Тогда получим неравенство:
аm/n<bm/n
Получили, что из двух степеней с одинаковыми показателями меньше та, у которой меньше основание (правила сравнения будем нумеровать, чтобы на них удобнее было ссылаться):
В частности, справедливы следующие неравенства:
233,75< 243,75
634/3< 644/3
0,0080,002< 0,0080,002
Здесь мы рассматривали случаи, когда показатель степени является положительным числом. А что делать, если он отрицательный? Тогда степень следует «перевернуть», воспользовавшись уже известной вам формулой:
a–n = 1/an = (1/а)n
Пример. Сравните выражения с рациональным показателем степени:
20–3,14 и 50–3,14
Решение. Избавимся от знака минус в показателе:
20–3,14 = (1/20)3,14 = 0,053,14
50–3,14 = (1/50)3,14 = 0,023,14
Получили две степени с одинаковым и, что принципиально важно, положительным показателем. Из них больше та, у которой больше основание. То есть из неравенства 0,02 < 0,05 следует, что
0,023,14< 0,053,14
Это означает, что
50–3,14< 20–3,14
Ответ: 50–3,14< 20–3,14.
Особенным является случай, когда показатель степени равен нулю. Напомним, что любое число в нулевой степени (кроме самого нуля) равно единице, а выражение 00 не имеет смысл. Это значит, что числа в нулевой степени равны друг другу, даже если у них разные основания:
250 = 260 = 1
9,360 = 9,370 = 1
18,35460 = 12,36470 = 1
Несколько сложнее сравнивать числа, у которых одинаковые основания, но различные показатели. Здесь возможны три случая – основание либо равно единице, либо больше неё, либо меньше неё.
На основании этого правила можно записать, что:
53,14< 53,15
45–0,563< 450,001
1,235–5,623< 1,235–4,958
Единица в любой степени равна самой себе. Поэтому, если у двух чисел в основании записана именно она, то они должны быть равны друг другу:
1–7,56 = 1–0,15 = 10,236 = 1 521,36 = 1
Осталось рассмотреть случай, когда основание меньше единицы (но всё равно положительное). В таком случае ситуация становится противоположной – чем больше степень, тем меньше число. Проиллюстрируем это на примере. Пусть надо сравнить числа 0,57,6 и 0,58,9. Заменим дробь 0,5 так, чтобы вместо нее получилась степень с основанием, большим единицы:
0,5 = 1/2 = 1/(21) = 2–1
Итак, 0,5 = 2–1. Тогда можно записать, что:
0,57,6 = (2–1)7,6 = 2–7,6
0,58,9 = (2–1)8,9 = 2–8,9
Такие числа мы уже умеем сравнивать. Так как
– 8,9 <– 7,6
то и
2–8,9< 2–7,6
Следовательно, 0,57,6> 0,58,9.
Например, справедливы неравенства:
0,997> 0,997,24
0,5715,36> 0,5716,47
0,490,04> 0,490,05
Рассмотрим чуть более сложное задание на сравнение степеней, где надо использовать одновременно несколько правил.
Пример. Докажите, что
0,90,9 + 0,80,8 + 0,70,7< 281/3
Решение. Напрямую вычислить значение выражений в правой и левой части затруднительно. Однако мы можем усиливать неравенство, чтобы получить более простые выражения.
Усилить неравенство – это значит увеличить его меньшую или уменьшить большую часть. Например, неравенство 10 < 20 усилится, если вместо 10 написать большее число (11 < 20), или вместо 20 написать меньшее число (10 < 19). Очевидно, что если усиленное неравенство верное, то и изначальное (ослабленное) также справедливо.
Очевидно, что можно легко посчитать значение выражения 271/3:
Также ясно, что 271/3< 281/3 (правило 1). Усилим исходное неравенство:
0,90,9 + 0,80,8 + 0,70,7< 271/3 (1)
Действительно, если (1) справедливо, то мы можем записать двойное неравенство
0,90,9 + 0,80,8 + 0,70,7< 271/3< 281/3
Опустив здесь среднюю часть, получим исходное неравенство. Так как 271/3 = 3, мы можем переписать (1) так:
0,90,9 + 0,80,8 + 0,70,7<3 (2)
Далее будем работать с левой частью. Очевидно, что 0,80,8< 0,90,8 (снова используем правило 1). С другой стороны, 0,90,8< 0,90,7 (правило 3). Значит, можно записать двойное неравенство:
0,80,8< 0,90,8<0,90,7
или просто 0,80,8<0,90,7. Абсолютно аналогично можно записать, что
0,70,8< 0,90,7<0,90,7
Или 0,70,8<0,90,7. Наконец, в силу правила (3), 0,90,9<0,90,7. Итак, имеем три неравенства:
0,90,9<0,90,7
0,80,8<0,90,7
0,70,8<0,90,7
Их левые части стоят в (2). Следовательно, можно усилить (2):
0,90,7 + 0,90,7 + 0,90,7<3
3•0,90,7< 3
Поделим обе части на 3:
0,90,7< 1
Заменим единицу равным ему выражением 10,7:
0,90,7<10,7 (4)
Из правила 1 следует, что (4) справедливо. Но мы получили его, усиливая исходное неравенство. Из справедливости более сильного неравенства следует и справедливость более слабого. Следовательно, из справедливости (4) вытекает верность исходного неравенства, которое и надо было доказать.
Как вычислить дробную степень
Вычисление дробных степеней порождает сложности, связанные с расчетами для отрицательных чисел. В связи с этим, математику для решения связанных с дробной степенью задач следует помнить ряд правил и рекомендаций.

Инструкция
Убедитесь в том, что задача вообще имеет решение. Если основание степени отрицательное, математика действительных чисел запрещает возведение в дробную степень. В этом случае нужно будет применять комплексное исчисление, которое изучают студенты высших технических улебных заведений.
В вычислении дробной степени имеется казус, по которому, с одной стороны, результат операции −8^1/3 не определен, но, с другой стороны, всем известно, что кубический дробными степенями, так как вы можете потерять отрицательные корни.
Если в задаче требуется произвести расчет дробной степени положительного числа, можно воспользоваться калькулятором с функцией возведения в степень, например, стандартным калькулятором Windows. Для этого введите основание степени, затем нажмите знаок возведения в степень, введите показатель степени и нажниме клавишу Enter. Результат будет выведен на экране калькулятора.
Если требуется решить уравнение, в котором один из аргументов присутствует в дробной степени, конкретный путь решения зависит от вида этого уравнения. Но нужно помнить несколько формул, которые помогают при вычислении дробной степени:A^BC = (A^B)^CA^(B+C) = A^B · A^Clog(A^B) = B · log(A)
В тех случаях, когда нужно найти приблизительное значение дробной степени числа, а калькулятора под рукой нет, воспользуйтесь формулами из пункта 4. Пример: найдем приблизительное значение 100^3/5. 100^3/5 = 10^6/5 = 1000000^1/5 ≈ 1024^1/5 · 1024^1/5 = 4*4 = 16. Проверяем на калькуляторе: 100^3/5 ≈ 15,85. Значение получено нами с неплохой точностью.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Какими свойствами обладает степень с дробным показателем (дробная степень)?
Как выполнить возведение числа в дробную степень?
Степенью числа a (где a>0) с рациональным показателем, который равен (n/m) называется число вида: , где где m — целое число, n — натуральное число (n>1).
Таким образом, число с дробным показателем степени равно корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю.
При этом a<0 степень с дробным показателем не определяется.
Чтобы извлечь корень из степени, надо показатель степени разделить на показатель корня.
Следовательно, если показатель степени не делится на показатель корня, то получается дробная степень.
Свойства степеней с дробным показателем
Все свойства степеней из курса алгебры 7 класса выполняются и для степеней с дробными показателями.
Для упрощения вычислений при возведении числа в дробную степень удобно использовать следующее свойство корня:
Чтобы было легче решать вычислять степени с дробным показателем:
Следует обратить внимание, что основание не может быть отрицательным числом, а показатель степени может быть как положительным, так и отрицательным.
Действия над степенями с дробными показателями
Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для степеней с целым показателем.
При умножении дробных степеней с одинаковыми основаниями их показатели складываются:
При делении дробных степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя:
Чтобы возвести степень в другую степень, в случае дробных показателей, достаточно перемножить показатели степеней:
Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:
Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.
Возведение числа в степень является важнейшей математической операцией, часто используемой для различных вычислений. В зависимости от вида основания и показателя значение степени рассчитывается по-разному. Ниже будут подробно рассмотрены основные правила нахождения значений степеней.
Возведение числа в степень с натуральным показателем
Прежде чем приступить к изучению операции возведения в степень необходимо рассмотреть базовое понятие натуральной степени числа.
Определение
Натуральной степенью n числа а называют произведение, состоящее из n множителей, каждый из которых равен a.
[a^{n}=underbrace{a times a times ldots times a}_{text {п множсителей }}]
Таким образом, для натурального показателя степень представляет собой укороченную запись умножения одинаковых множителей. В данном случае чтобы найти значение степени, следует перемножить число, которое является основанием, само на себя указанное количество раз.
Пример 1
Рассмотрим возведение числа 3 в степень 5. Согласно приведенному выше базовому определению:
35 = 3 × 3 × 3 × 3 × 3 = 243
Для операций возведения во вторую и третью степень имеются устоявшиеся названия: возведение в квадрат и куб, соответственно. Таким образом, выражение «32» может быть прочитано как «три во второй степени» или «три в квадрате», оба варианта будут верными.
Значение степенных выражений с дробным основанием и натуральным показателем находится по той же схеме. В то же время, в соответствии с правилом умножения дробей, операция возведения дроби в степень может быть разбита на два действия, когда числитель и знаменатель возводятся в соответствующую показателю степень по отдельности.
Пример 2
Найдем, чему будут равны [ frac{2}{5} ] в степени 3:
[left(frac{2}{5}right)^{3}=frac{2}{5} times frac{2}{5} times frac{2}{5}=frac{2^{3}}{5^{3}}=frac{8}{125}]
Операция возведения в натуральную степень имеет определенные особенности при работе с отрицательными числами. Рассмотрим следующий пример:
Пример 3
Найдем значения степенных выражений (-5)3 и (-5)4. Для этого, согласно базовому определению, необходимо умножить основание само на себя 3 и 4 раза соответственно:
(-5)3 = (-5) × (-5) × (-5) = -125
(-5)4 =(-5) × (-5) × (-5) × (-5) = 625
Из приведенного примера можно видеть, что в первом случае полученный результат является отрицательным числом, а во втором – положительным. Это связано с правилом перемножения отрицательных чисел. Следствием из него является то, что если показатель степени отрицательного числа представляет собой четное число, результат будет положительным, если нечетное – отрицательным. Таким образом, степень с отрицательным основанием и четным показателем будет равна степени с таким же показателем и основанием, равным по модулю, но противоположным по знаку.
(-a)2n = a2n
Если требуется возвести в натуральную степень иррациональное число, то его необходимо предварительно округлить до той значащей цифры, которая позволит получить ответ с требуемой точностью. Рассмотрим данный случай на примере числа π.
Пример 4
Выполним возведение в степень 3 числа π.
π – это бесконечное иррациональное число. С точностью до 10 знаков после запятой оно записывается следующим образом:
π = 3,1415926536
Допустим, нам необходим результат с точностью два знака после запятой. Тогда число π может быть округлено до 3,14.
(3,14)3 = 3,14 × 3,14 × 3,14 ≈ 30,96
Отдельно следует отметить, чему будет равно число в степени 1. В соответствии с базовым определением
[a^{n}=underbrace{a times a times ldots times a}_{text {п множсителей }}]
вне зависимости от значения основания, число в степени 1 равно самому себе.
На практике возможны и более сложные случаи, когда требуется найти значение степенного выражения, в котором показатель не является натуральным числом. Ниже будут рассмотрены ситуации, когда показатель степени представляет собой целое, дробное, рациональное или иррациональное число.
Вычисление степеней с целым показателем
Все операции по возведению в целую степень можно разделить на три группы: когда показатель является целым положительным (натуральным) числом, когда он равен нулю, и когда он является отрицательным числом.
Случай с натуральным показателем был рассмотрен ранее, поэтому мы не будем к нему возвращаться.
В случае, когда показатель равен нулю, для любого не равного нулю основания значение степени будет равно единице. Если же и основание, и показатель степени равны нулю значение выражения будет не определено.
Пример 5
Рассмотрим возведение в нулевую степень натурального, дробного, иррационального чисел, а также нуля:
100 = 1
0,50 = 1
π0 = 1
00 – не определено.
Осталось рассмотреть нахождение значения степенного выражения с целым отрицательным показателем. Число а в степени -n представляет собой дробь, числитель которой равен единице, а знаменатель – числу а в степени n.
[a^{-n}=frac{1}{a^{n}}]
Можно видеть, что знаменатель дроби является натуральной степенью, вычисление которой было рассмотрено ранее. Таким образом, две степени, у которых основания одинаковы, а показатели противоположны по знаку, но равны по модулю, будут являться обратными числами. Рассмотрим возведение в отрицательную степень целого и дробного чисел:
Пример 6
Вычислим, чему равно 7 в степень -3:
[7^{-3}=frac{1}{7^{3}}=frac{1}{7 times 7 times 7}=frac{1}{343}]
Пример 7
Найдем значение степенного выражения [left(frac{2}{9}right)^{-2}]
При возведении дробного числа в отрицательную степень на определенном этапе осуществляется «переворот» дроби. Он может быть выполнен как в конце вычислений:
[left(frac{2}{9}right)^{-2}=frac{1}{left(frac{2}{9}right)^{2}}=frac{1}{frac{2}{9} times frac{2}{9}}=frac{1}{frac{4}{81}}=frac{81}{4}=20 frac{1}{4}]
так и в начале:
[left(frac{2}{9}right)^{-2}=left(frac{9}{2}right)^{2}=frac{81}{4}=20 frac{1}{4}]
Из-за указанного в примере «переворота», при возведении десятичной дроби в отрицательную степень рекомендуется предварительно преобразовать основание к форме обыкновенной дроби. Рассмотрим данную ситуацию на примере:
Пример 8
Найдем значение степенного выражения 0,5-2:
[0,5^{-2}=left(frac{5}{10}right)^{-2}=left(frac{10}{5}right)^{2}=frac{10^{2}}{5^{2}}=frac{100}{25}=4]
Отдельно следует упомянуть о выражениях с целым отрицательным показателем, основание которых равно нулю. Подобное выражение будет не определено, поскольку его преобразование будет приводить к дроби, знаменатель которой равен нулю.
[0^{-n}=frac{1}{0^{n}}] ‒ выражение не определено.
Возведение числа в дробную степень
Прежде чем приступить к вычислению, следует рассмотреть базовое определение степени с дробным показателем. В виде формулы оно может быть записано следующим образом:
[a^{m / n}=sqrt[n]{a^{m}}, text { где }]
a – положительное число;
m – целое число;
n – натуральное число.
Из указанного определения следует, что операция нахождения алгебраического корня любой степени также может быть представлена в форме возведения в дробную степень, когда числитель показателя равен единице, а знаменатель – основанию корня.
[sqrt[n]{a}=a^{1 / n}]
При этом не следует воспринимать данное свойство как способ преобразования иррационального числа в рациональное. Изменяется только форма записи. Например, если число √2 является иррациональным, то при записи его в форме [2^{1 / 2}] оно также останется иррациональным.
При нахождении значения степени с дробным показателем следует последовательно выполнить два математических действия: возведение основания в степень с целым показателем m и извлечение корня n-ной степени. При этом согласно свойству корней, указанные действия можно выполнить и в обратной последовательности, то есть можно сначала извлечь из основания корень n-й степени, а затем возвести полученный результат в степень m.
[sqrt[n]{a^{m}}=(sqrt[n]{a})^{m}]
Рассмотрим оба способа вычисления степеней с дробным показателем на конкретном примере.
Пример 9
Найдем значение степенного выражения [128^{5 / 7}].
Способ 1. Возведение в степень подкоренного выражения с последующим извлечением корня
[128^{5 / 7}=sqrt[7]{128^{5}}=sqrt[7]{34359738368}=32]
В данном случае из-за большого значения числа под корнем найти значение выражения, не прибегая к помощи калькулятора, невозможно.
Способ 2. Извлечение корня из основания с последующим возведением в степень.
[128^{5 / 7}=(sqrt[7]{128})^{5}=2^{5}=32]
Указанный способ нахождения значения степени существенно легче. При этом результат вычислений не отличается, то есть можно выбирать тот способ, который будет удобнее в конкретном случае.
Если показатель степени представлен в форме десятичной дроби, то удобнее будет записать его в виде обычной.
Пример 10
Вычислим значение степени [243^{0,4}]:
[243^{0,4}=243^{4 / 10}=243^{2 / 5}=(sqrt[5]{243})^{2}=3^{2}=9]
В случае, когда показатель представляет собой смешанное число, для удобства вычислений он может быть записан в виде неправильной дроби.
Пример 11
Вычислим значение выражения:
[left(12 frac{1}{4}right)^{1 frac{1}{2}}=left(frac{49}{4}right)^{3 / 2}=left(sqrt{frac{49}{4}}right)^{3}=left(frac{7}{2}right)^{3}=frac{343}{8}=42 frac{7}{8}]
Следует обратить внимание на математическую операцию возведения в отрицательную дробную степень. В этом случае вычисления производятся в три этапа: нахождение числа, обратного исходному, извлечение корня, степень которого соответствует значению знаменателя показателя, и возведение в степень, соответствующую числителю дробного показателя. Как и в случае с положительным дробным показателем, указанные действия могут выполняться в любой последовательности.
Пример 12
Найдем значение выражения [49^{-1 / 2}].
Выполним преобразование числа в обратное ему:
[49^{-1 / 2}=frac{1}{49^{1 / 2}}]
Найдем значение степени в знаменателе полученной дроби:
[frac{1}{49^{1 / 2}}=frac{1}{sqrt{49}}=frac{1}{7}]
Также необходимо рассмотреть случай, когда основанием степени является ноль, а показателем – дробное число. Как и в случае с целыми показателями, подобные выражения имеют смысл лишь в том случае, когда показатель больше нуля. В противном случае выражение будет не определено.
Нет времени решать самому?
Наши эксперты помогут!
Нахождение степеней с иррациональным показателем
Иногда возникает необходимость нахождения значения степени, показатель которой представляет собой иррациональное число. Проблема заключается в том, что найти точное значение подобного выражения невозможно. Однако для решения любой практической задачи, как правило, достаточно нахождения значения степенного выражения с определенной степенью точности. В этом случае иррациональный показатель округляется до требуемого десятичного знака, после чего вычисление осуществляется согласно правилам, принятым для дробного показателя.
Рассмотрим решение подобной задачи на конкретном примере:
Пример 13
Предположим, что нам необходимо найти значение выражения 2 в степени √2. Показатель степени является иррациональным числом. В виде бесконечной десятичной дроби оно может быть записано следующим образом:
√2 = 1,41421356…
Найдем значение выражения с различной степенью приближения.
Вариант 1.
Округлим значение иррационального числа до двух цифр после запятой и найдем приближенное значение степени:
[√2≈1,41]
[2^{sqrt{2}} approx 2^{1,41} approx 2,65737]
Вариант 2.
Округлим значение иррационального числа до четырех цифр после запятой и найдем приближенное значение степени:
[√2≈1,4142]
[2^{sqrt{2}} approx 2^{1,4142} approx 2,66512]
Можно видеть, что полученные значения различаются во втором знаке после запятой, при этом второе значение является более точным.
В большинстве случаев вычисление степеней с иррациональными показателями является сложной задачей, для решения которой используется вычислительная техника.