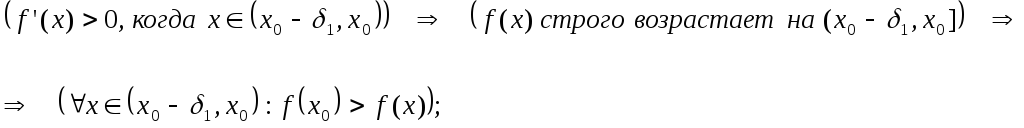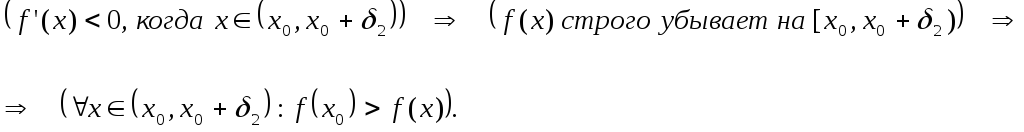Как найти стационарные точки функции 11 класс

Значит, производная меняет знак только в точках (x=0) и (x=2).

В точке (x=0) она меняет знак с положительного на отрицательный, значит, это точка локального максимума со значением функции (f(0)=0).

В точке (x=2) она меняет знак с отрицательного на положительный, значит, это точка локального минимума со значением функции (f(2)=4).

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Алгебра и начала математического анализа, 11 класс

Урок № 16. Экстремумы функции.

Перечень вопросов, рассматриваемых в теме

1) Определение точек максимума и минимума функции

2) Определение точки экстремума функции

3) Условия достаточные для нахождения точек экстремума функции

Глоссарий по теме

Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х₁ и х₂, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Максимум функции. Значение функции в точке максимума называют максимумом функции 

Минимум функции. Значение функции в точке минимума называют минимумом функции 

Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).

Точка максимума функции. Точку  х₀ называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство  .

Точка минимума функции. Точку  х₀ называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство  .

Точки экстремума функции. Точки минимума и максимума называют точками экстремума.

Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х₁ и х₂, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Алгоритм исследования функции на монотонность и экстремумы:

1) Найти область определения функции D(f)

2) Найти f’ (x).

3) Найти стационарные (f'(x) = 0) и критические (f'(x) не

существует) точки функции y = f(x).

4) Отметить стационарные и критические точки на числовой

прямой и определить знаки производной на получившихся

промежутках.

5) Сделать выводы о монотонности функции и точках ее

экстремума.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.

• Точку х = х₀ называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x₀).
• Точку х = х₀ называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x₀).

Точки максимума и минимума – точки экстремума.

Функция может иметь неограниченное количество экстремумов.

Критическая точка – это точка, производная в которой равна 0 или не существует.

Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.

Алгоритм нахождения максимума/минимума функции на отрезке:

1. найти экстремальные точки функции, принадлежащие отрезку,
2. найти значение функции в экстремальных точках из пункта 1 и в концах отрезка,
3. выбрать из полученных значений максимальное и минимальное.

Примеры и разбор решения заданий тренировочного модуля

№1. Определите промежуток монотонности функции у=х² -8х +5

Решение: Найдем производную заданной функции: у’=2x-8

2x-8=0

х=4

Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)

Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)

№2. Найдите точку минимума функции у= 2х-ln(х+3)+9

Решение: Найдем производную заданной функции:

Найдем нули производной:

х=-2,5

Определим знаки производной функции и изобразим на рисунке поведение функции:

Ответ: -2,5 точка min

№3. Материальная точка движется прямолинейно по закону x(t) = 10t² − 48t + 15, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.

Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени. 

V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 мc

Ответ: V=12 мc

№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.

Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3

Ответ: 3

Сегодня на уроке мы выясним, какая точка называется точкой
максимума функции, а также узнаем, какая точка называется точкой минимума
функции. Сформулируем теорему Ферма. Приведём достаточные условия того, что
стационарная точка является точкой экстремума.

Прежде чем приступить к рассмотрению новой темы, давайте вспомним,
что на нашем прошлом занятии мы исследовали на возрастание и убывание функцию .

Сейчас вы видите график этой функции.

Давайте рассмотрим окрестность точки , то
есть некоторый интервал, содержащий эту точку. Из рисунка видно, что существует
такая окрестность точки , что
наибольшее значение данная функция в этой окрестности принимает в точке .
Например, на интервале  функция
принимает наибольшее значение, равное , в
точке .
Таким образом, точку  называют
точкой максимума функции.

Рассмотрим окрестность точки . Из
рисунка видно, что существует такая окрестность точки , что
наименьшее значение данная функция в этой окрестности принимает в точке .
Например, на интервале  функция
принимает наименьшее значение, равное , в
точке .
Точку  называют
точкой минимума функции.

Сформулируем определение.

Точка  называется
точкой максимума функции , если
существует такая окрестность точки , что
для всех  из
этой окрестности выполняется неравенство .

Так, например, точка  является
точкой максимума функции , так
как  и при
всех значениях  верно
неравенство .

Точка  называется
точкой минимума функции , если
существует такая окрестность точки , что
для всех  из
этой окрестности выполняется неравенство .

Например, точка  является
точкой минимума функции , так
как  и при
всех значениях  верно
неравенство .

Точки минимума и точки максимума называются точками экстремума.

Теперь познакомимся с теоремой Ферма. Пусть функция  определена
в некоторой окрестности точки  и
имеет производную в этой точке. Тогда сформулируем утверждение, которое и
называют теоремой Ферма.

Если  – точка экстремума дифференцируемой
функции , то .

Доказательство этой теоремы приводится в курсе высшей математики.

Геометрический смысл теоремы

Например, рассмотренная выше функция  имеет
максимум в точке . .

Функция  имеет
минимум в точке . , .

Таким образом, мы убедились, что значение производной в точке
экстремума функции равно нулю.

Но отметим, что если , то
этого недостаточно, чтобы утверждать, что  обязательно
является точкой экстремума функции .

Так, например, производная функции  равна
.
Производная равна 0 в точке 0. Однако точка  не
является точкой экстремума, так как данная функция возрастает на всей числовой
оси.

Получается, что не всегда корень уравнения  является
точкой экстремума. Но точки экстремума дифференцируемой функции нужно искать
только среди корней уравнения .

Точки, в которых производная равна нулю, называют стационарными.

Из предыдущих занятий вам известно, что функция  не
имеет производной в точке . При
этом эта точка является точкой минимума данной функции.

Точки, в которых функция имеет производную, равную нулю, или
недифференцируема, называют критическими точками этой функции.

То есть точка  –
критическая точка функции .

Таким образом, чтобы точка  была
точкой экстремума функции ,
необходимо, чтобы эта точка была критической точкой данной функции.

Теперь приведём достаточные условия того, что стационарная
точка является точкой экстремума. Это будут условия, при выполнении которых
стационарная точка является точкой максимума или минимума.

Итак, пусть функция  дифференцируема
на интервале ,  и .
Тогда:

1) если при переходе через стационарную точку  функции
 её
производная меняет знак с «плюса» на «минус», то есть  слева
от точки  и  справа
от точки , то  –
точка максимума функции ;

2) если при переходе через стационарную точку  функции
 её
производная меняет знак с «минуса» на «плюс», то  –
точка минимума функции .

Давайте найдём точки экстремума функции  и значения функции в этих точках.

А сейчас выполним несколько заданий.

Задание первое. Найдите стационарные
точки функций:

а) ; б) .

Решение.

Задание второе. Найдите точки
экстремума функций:

а) ; б) .

Решение.

1. Стационарные точки функции.
   Необходимое условие локального
   экстремума функции

2. Первое достаточное условие локального
   экстремума

3. Второе и третье достаточные условия
   локального экстремума

4. Наименьшее и наибольшее
   значения функции на сегменте

5. Выпуклые функции и точки перегиба

1. Стационарные точки функции. Необходимое условие локального экстремума функции

_{Определение 1.}
Пусть функция
определена на _{.
Точка
называется стационарной точкой функции
,
если
дифференцирована в точке
и .}

Теорема 1 (необходимое
условие локального экстремума функции).
Пусть функция
определена на
_{и имеет в точке
локальный экстремум. Тогда выполняется
одно из условий:}

1. функция
   _{не имеет в точке
   производной;}

2. функция
   _{имеет в точке
   производную и .}

_{Таким образом, для того,
чтобы найти точки, которые являются
подозрительными на экстремум, надо
найти стационарные точки функции и
точки, в которых производная функции
не существует, но которые принадлежат
области определения функции.}

_{Пример.
Пусть .
Найти для нее точки, которые являются
подозрительными на экстремум. Для
решения поставленной задачи, в первую
очередь, найдем область определения
функции: .
Найдем теперь производную функции:}

_.

_{Точки, в которых производная
не существует: .
Стационарные точки функции:}

_.

_{Поскольку и ,
и
принадлежат области определения функции,
то они обе будут подозрительными на
экстремум. Но для того, чтобы сделать
вывод, будет ли там действительно
экстремум, надо применять достаточные
условия экстремума.}

2. Первое достаточное условие локального экстремума

Теорема 1 (первое достаточное
условие локального экстремума).
Пусть функция
определена на
_{и дифференцирована на этом интервале
везде за исключением, возможно, точки
,
но в этой точке
функция является
непрерывной. Если
существуют такие правая и левая
полуокрестности точки ,
в каждой из которых
сохраняет определенный знак, то}

_{1) функция
имеет локальный экстремум в точке ,
если
принимает значения разных знаков в
соответствующих полуокрестностях;}

<sub>2) функция
не имеет локальный экстремум в точке
,
если справа и слева от точки

имеет одинаковый знак.</sub>

_{Доказательство.
1) Предположим, что в полуокрестности
производная ,
а в
.}

_{Таким образом в точке
функция
имеет локальный экстремум, а именно —
локальный максимум, что и нужно было
доказать.}

_{2) Предположим, что слева
и справа от точки
производная сохраняет свой знак,
например, .
Тогда на
и
функция
строго монотонно возрастает, то есть:}

_,

_.

_{Таким образом экстремума
в точке
функция
не имеет, что и нужно было доказать.}

_{Замечание 1.
Если производная
при прохождении через точку
меняет знак с «+» на «-», то в точке
функция
имеет локальный максимум, а если знак
меняется с «-» на «+», то локальный
минимум.}

_{Замечание 2.
Важным является условие непрерывности
функции
в точке .
Если это условие не выполняется, то
теорема 1 может не иметь места.}

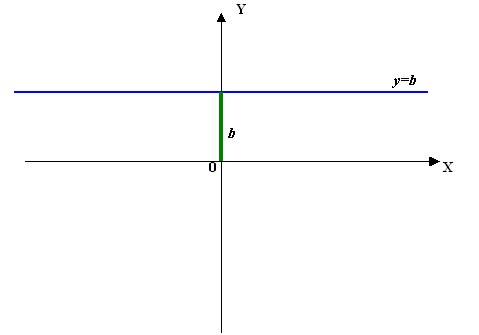
_{Пример.
Рассматривается функция (рис.1):}

Эта функция определена на
<sub>и непрерывна везде, кроме точки ,
где она имеет устранимый разрыв. При
прохождении через точку

меняет знак с «-» на «+», но локального
минимума в этой точке функция не имеет,
а имеет локальный максимум по определению.
Действительно, около точки
можно построить такую окрестность, что
для всех аргументов из этой окрестности
значения функции будут меньше, чем
значение .
Теорема 1 не сработала потому, что в
точке
функция имела разрыв.</sub>

_{Замечание 3.
Первое достаточное условие локального
экстремума не может быть использовано,
когда производная функции
меняет свой знак в каждой левой и каждой
правой полуокрестности точки .}

_{Пример.
Рассматривается функция:}

_{Поскольку ,
то ,
а потому ,
но .
Таким образом:}

_,

_{т.е. в точке
функция
имеет локальный минимум по определению.
Посмотрим, сработает ли здесь первое
достаточное условие локального
экстремума.}

_{Для :}

_.

Для первого слагаемого правой
части полученной формулы имеем:

_,

_{а потому в малой окрестности
точки
знак производной определяется знаком
второго слагаемого, то есть:}

_,

<sub>а это означает, что в любой
окрестности точки

будет принимать как положительные, так
и отрицательные значения. Действительно,
рассмотрим произвольную окрестность
точки :
.
Когда</sub>

_,

_то

_{(рис.2), а
меняет свой знак здесь бесконечно много
раз. Таким образом, нельзя использовать
в приведенном примере первое достаточное
условие локального экстремума.}

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #