Как найти стационарную концентрацию

В рассмотренном выше простейшем случае
двух последовательных реакций первого
порядка получены уравнения для
концентрации промежуточного и конечного
продуктов, которые нельзя строго решить
относительно констант скорости, т.е.
невозможно рассчитывать последние
непосредственно из экспериментальных
данных о зависимости концентрации от
времени. В более сложных случаях
нескольких последовательных реакций
разного порядка строгое математическое
описание кинетики часто оказывается
невозможным.

Для описания кинетики многостадийных
реакций можно использовать приближенный
метод стационарных концентрацийБоденштейна. В основе метода лежит
положение о том, чточерез некоторое
небольшое время после начала реакции
скорость образования промежуточного
продукта становится примерно равной
скорости его распада и суммарную скорость
изменения концентрации неустойчивого
промежуточного продукта можно считать
приблизительно равной нулю в течение
достаточно длительного времени, т.е.
в течение этого времениустанавливается
стационарная концентрация неустойчивого
продукта.

Рассмотрим, например, некоторую реакцию

А + В 2С,

которая протекает с образованием двух
промежуточных продуктов М₁и М₂по схеме:

1) А 2М₁k₁

2) М₁+ ВС +
М₂k₂

3) М₂+ АС
+ М₁k₃

4) М₁+ М₁Аk₄

Обозначим через c_oAиc_oBисходные концентрации веществ А и В,
черезc_i– текущие
концентрации всех участников реакции.
Используя предложенную схему реакции,
запишем выражения для уменьшения
концентраций А и В и увеличения
концентрации С с течением времени:

, (20.74)

, (20.75)

. (20.76)

Скорости изменения концентрации
промежуточных продуктов М₁и М₂соответственно равны:

, (20.77)

. (20.78)

Считая, что концентрации промежуточных
продуктов
в
течение реакции малы и учитывая
стехиометрическое уравнение, можно
записать:

, (20.79)

. (20.80)

Тогда, после дифференцирования по
времени, получим:

, (20.81)

. (20.82)

Подставим в уравнение (20.81) значения
скоростей (20.74) и (20.77):

(20.83)

или

. (20.84)

Последнее выражение совпадает с
уравнением (20.77) для скорости образования
промежуточного продукта М₁, откуда
следует, что

. (20.85)

Аналогично, подставив в уравнение
(20.82) значения скоростей (20.74) и (20.75) и
сравнивая с (20.77), получим

. (20.86)

Уравнения (20.85) и (20.86) и являются выражениями
принципа стационарности.

В заключение заметим, что метод
стационарных концентраций не является
совершенно строгим, его применение
ограничивается выполнением условий
типа (20.78), (20.79), т.е. образованием очень
неустойчивых промежуточных продуктов,
концентрация которых в ходе реакции
оказывается небольшой. Однако на практике
такие случаи встречаются очень часто
(образование в качестве промежуточных
продуктов атомов, свободных радикалов),
поэтому метод стационарных концентраций
получил широкое распространение при
изучении кинетики и механизма различных
реакций.

20.7. Влияние температуры на скорость химических реакций

В большинстве случаев повышение
температуры приводит к увеличению
константы скорости химической реакции.
Согласно правилу Вант-Гоффатемпературный коэффициент скорости,
т.е. отношение констант скоростей реакции
при температурахTиT+ 10, изменяется
в пределах от 2 до 4:

. (20.87)

В общем случае изменения температуры
от TдоT+ 10n, гдеn–
положительное или отрицательное, целое
или дробное число, для температурного
коэффициента можно записать:

. (20.88)

Правило Вант-Гоффа получено эмпирически
и является приближенным. Значения
температурного коэффициента не остаются
постоянными при изменении температуры
и стремятся к единице при высоких
температурах. Поэтому правило можно
использовать для полуколичественных
оценок в области сравнительно низких
температур.

Более точно зависимость константы
скорости от температуры передается
уравнением Аррениуса:

, (20.89)

где ВиС– постоянные, характерные
для данной реакции и не зависящие от
температуры.

Уравнение Аррениуса также было получено
вначале эмпирически, а затем обосновано
теоретически.

При выводе уравнения Аррениус предположил,
что реагировать могут не все молекулы,
а лишь некоторые из них, находящиеся в
особом активном состоянии. Эти молекулы
образуются из обычных в эндотермическом
процессе с поглощением тепла E_A.
Так, например, в реакции

A B

активные молекулы А* образуются из
нормальных молекул А по схеме:

A L
A* + E_A

По Аррениусу, этот процесс является
обратимым и быстрым, так что в системе
всегда сохраняется термодинамическое
равновесие между А и А*, которое можно
характеризовать константой равновесия
K_c:

или [A*] = K_c[A]. (20.90)

Предполагается, что концентрация
активной формы мала, и равновесная
концентрация [А] исходных молекул А
практически равна текущей концентрации
c_A[А].
Изменение константы равновесия с
температурой описывается уравнением
изохоры Вант-Гоффа

. (20.91)

Последнее допущение Аррениуса заключается
в том, что превращение активных молекул
в конечный продукт осуществляется со
скоростью, не зависящей от температуры
и относительно медленно:

[A*] B

Таким образом, скорость образования
вещества В равна

, (20.92)

где k’– константа скорости, не
зависящая от температуры.

С другой стороны, согласно основному
постулату химической кинетики скорость
реакции А В равна

, (20.93)

где k– определяемая экспериментально
константа скорости, которая зависит от
температуры.

Сравнивая уравнения (20.92) и (20.93) и учитывая
все ранее сделанные допущения, получим:

. (20.94)

Отсюда следует, что экспериментальная
константа скорости

k = k’c або lnk= lnk’+ lnK_c. (20.95)

Так как k’не зависит от температуры,
то дифференцируя поT, получим

. (20.96)

Используя уравнение Вант-Гоффа (20.91),
приходим к уравнению Аррениуса в
дифференциальной форме:

. (20.97)

Величина E_Aназываетсяэнергией активации, или опытной
энергией активации. В рамках изложенных
представлений – это то количество
теплоты, которое необходимо, чтобы
перевести один моль молекул, находящихся
в нормальном состоянии, в особую активную,
реакционно-способную форму.

Интегрируя уравнение (20.96) в предположении
независимости энергии активации от
температуры, получим:

, (20.98)

где С– константа интегрирования.

Полученное уравнение совпадает с
эмпирическим уравнением Аррениуса
(20.89), в котором постоянная Всоответствует значениюE_A/RилиE_A=ВR. Потенцируя
уравнение (20.98), можно представить его
в экспоненциальной форме, полагаяe^C= A:

. (20.99)

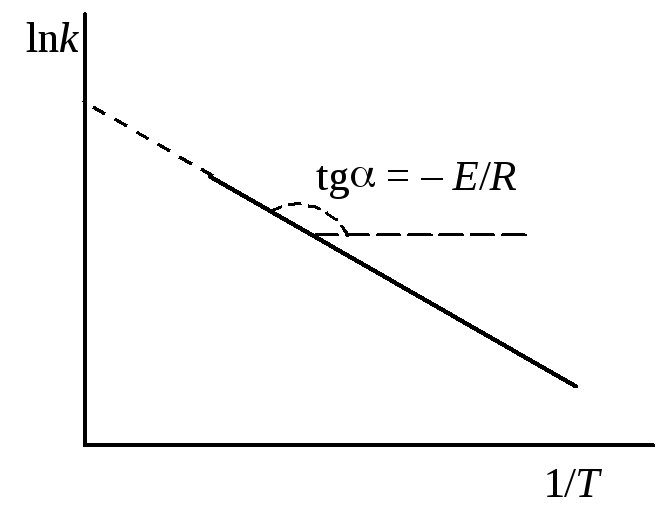
Рис. 20.6. Зависимость
lnk
от 1/T

Рис. 20.7. Зависимость
lnk
от 1/T для параллельных реакций

Как видно из уравнения (20.97), логарифм
константы скорости является линейной
функцией обратной температуры. Поэтому
для экспериментального определения E_Aнаходят константы скорости реакции при
нескольких температурах и строят
зависимость в координатах lnk– 1/T(рис. 20.6). Отрезок, отсекаемый прямой на
оси ординат, равен константеС, а
энергия активации вычисляется по
тангенсу угла наклона прямой.

Если известны константы скорости реакции
только при двух температурах T₁иT₂, энергию активации можно
вычислить из соотношения, которое
получается интегрированием уравнения
(20.97) в пределах этих температур:

, (20.100)

где k₁иk₂– константы
скорости при температурахT₁иT₂соответственно.

В некоторых случаях график зависимости
lnk– 1/Tимеет иной вид – он состоит
как бы из двух пересекающихся прямых с
разным наклоном, что свидетельствует
о сложном характере реакции. Например,
водород может реагировать как с жидкой,
так и с газообразной серой. Если в сосуде
одновременно присутствуют водород,
жидкая сера и ее пары, то при низких
температурах протекает реакция водорода
с жидкой серой с меньшей энергией
активации (отрезок 1 на рис. 20.7), а при
более высоких температурах – реакция
водорода с парами серы с большей энергией
активации (отрезок 2).

Экспериментальные исследования
показывают, что энергии активации
реакций с валентнонасыщенными молекулами
составляют от нескольких десятков до
сотен (50 500) кДж/моль.
При этом не обнаружено каких-либо простых
закономерностей, связывающих энергию
активации с какими-нибудь другими
характеристиками реакции, например, с
тепловым эффектом. В реакциях, протекающих
через элементарные стадии с участием
свободных атомов и радикалов, энергии
активации значительно ниже (1050 кДж/моль).

В некоторых случаях повышение температуры
приводит к снижению скорости реакции.
Примером может служить реакция

2NO + O₂
 2NO₂
,

которая является одной из стадий
получения азотной кислоты. Аномальный
ход температурной зависимости константы
скорости этой реакции можно объяснить,
предположив, что она протекает в две
стадии:

I. 2NO LN₂O₂(быстрая, обратимая, экзотермическая)

II. N₂O₂+ O₂2NO₂(медленная)

Общая скорость реакции определяется
скоростью второй, более медленной
стадии:

.

Концентрация димера N₂O₂зависит от константы равновесия,
устанавливающегося на первой стадии:

или.

Тогда

.

Это уравнение соответствует экспериментально
установленному третьему порядку реакции.
Так как первая стадия экзотермична, то
константа равновесия K_cуменьшается при повышении температуры.
Если это уменьшение перекрывает возможное
увеличениеk, то это и приведет к
общему снижению скорости реакции.

Понятия стационарного и квазистационарного режимов

В открытой системе может установиться стационарный режим с постоянными концентрациями промежуточных веществ в данной точке пространства. В таких условиях скорости образования и расходования промежуточных веществ одинаковы:

Иногда для закрытых систем можно применить понятие квазистационарного режима.

Двустадийная последовательная реакция имеет вид:

При $k_1ll k_2$, $tau >{tau }_{max}$, тогда

то есть отношение $frac{C_p}{C_A}=frac{k_1}{k_2} $= const.

Так как с течением времени отношение концентрации промежуточного вещества и исходного вещества не изменяется, считается, что реакция протекает в квазистационарном состоянии. Концентрацию промежуточного вещества обычно трудно определить, так как она включена в систему дифференциальных уравнений. Используя полученные соотношения концентрацию промежуточного реагента можно выразить через концентрацию исходного реагента.

Большинство многостадийных реакций содержат стадии, в которыхпринимают участие активные частицы — радикалы, атомы, возбужденные молекулы и др. Данные элементарные реакции идут гораздо быстрее, чем реакции молекул, не имеющих свободных валентностей.

В максимуме концентрация активных частиц невелика. Так как разность между скоростями образования и расходования будет невелика по сравнению с самими скоростями, то около максимума и после него концентрация будет меняться незначительно.

Это облегчает анализ кинетической прямой и является основой метода квазистационарных концентраций Боденштейна.

Принцип стационарных концентраций Боденштейна — Семенова

Принцип стационарных концентраций: если реакция протекает в несколько стадий с образованием промежуточных продуктов, имеющих небольшие концентрации, то можно допустить, что концентрации стационарны, то есть не меняются со временем.

Разность скоростей образования промежуточного вещества и его расходования будет мала по сравнению с самими скоростями образования и расходования промежуточных веществ, поэтому может быть приравнена к нулю:

Рассмотрим систему с последовательно протекающими реакциями:

1 стадия:

• прямая реакция $A+B{{stackrel{k_1}{longrightarrow}}}P,$

• обратная реакция $P{{underset{k_{-1}}{longrightarrow}}}$ $A+B$.

2 стадия: $P{{stackrel{k_2}{longrightarrow} }}C.$

Известно, что $k_1ll k_2.$

Промежуточный реагент будет накапливаться по прямой реакции $1$ стадии и расходоваться по $2$ стадии и обратной реакции $1$ стадии. Выразим дифференциальное уравнение для скорости образования промежуточного продукта через применение условия стационарности:

Тогда концентрация промежуточного вещества:

Применим это выражение для скорости накопления продукта реакции:

Соотношение констант скоростей можно показать как эффективную константу скорости:

Тогда закон скорости имеет вид:

Формально реакция описывается уравнением второго порядка. При использовании принципа стационарности упрощается описание кинетики, но теряется информация о константах элементарных стадий.

Для формирования квазистационарного режима необходимо время с начала реакции $tau _{ст.}$ Его величину можно определить исходя из условия

в котором

При решении этого уравнения находим

где $gamma =frac{k_2}{k_1}.$

Время достижения максимума концентрации промежуточного вещества равно времени установления квазистационарного состояния.

Применение принципа стационарности

Несмотря на неточность принципа стационарных состояний, он нашел применение в кинетике цепных и других сложных реакций.

Применение принципа стационарности упрощает расчеты и позволяет получать результаты, согласующиеся с опытными данными.

    Если концентрации обоих промежуточных веществ В и D в любой момент времени малы по сравнению с концентрациями А и С, можно применить метод стационарного состояния. Стационарные концентрации В и D определяются из соотношений [c.56]

    Смысл этого результата состоит не в том, что молекулы с энергией, меньшей Е, могут реагировать, а в том, что экспериментальная энергия активации должна представлять собой разность средней энергии реагирующих и нормальных молекул. При низких давлениях константа скорости реакции молекул с энергией, превышающей Е, так велика по сравнению со скоростью их образования, что стационарная концентрация таких молекул пренебрежимо мала по сравнению с концентрацией молекул с энергиями, близкими к Е. Так как в среднем молекула имеет энергию skT, то при очепь низких давлениях средняя реагирующая молекула имеет энергию + кТ. Разность равна — (s—1) кТ, и она отличается от Е — (s—3/2) кТ на величину 1/2 кТ, которая обусловлена температурной зависимостью частоты столкновения. [c.214]

    Если пренебречь периодом установления стационарного состояния, который, как не трудно показать, незначителен [6] при всех температурах ниже 1000° К, тогда можно применить метод стационарных концентраций [c.284]

    Несмотря на то что введение дополнительных реакций инициирования и обрыва цепи усложняет анализ схемы, в алгебраические выражения по-прежнему входит концентрация радикалов в первой степени и уравнение для стационарных концентраций, несмотря на громоздкий вид, может быть, легко разрешено. Однако при рассмотрении более чем одной реакции обрыва, в том числе бимолекулярной рекомбинации двух радикалов, уравнения становятся нелинейными и точные решения не всегда возможны. Допустим, нанример, что в упрощенную схему [см. уравнение (Х1П.10.5)] включены дополнительные реакции обрыва  [c.316]

    Пользуясь методом стационарных концентраций и предполагая, что длина цепи велика , можно показать, что [c.294]

    Хотя мы и не касаемся непосредственно механизма реакций, нри обсуждении вопроса, является ли стехиометрическое уравнение данной реакции полным, существенную помощь могут оказать простейшие представления о ее механизме. Пусть, например, реакция Л —> 5 идет в присутствии катализатора, например, энзима Е. Будем считать, что процесс в действительности проходит в две стадии сначала А и Е образуют комплекс С, а затем С диссоциирует на В VI Е. Тогда реакция А В заменяется на две реакции А Е С и С —> 5 -Ь . Если скорость реакции зависит только от текущих (мгновенных) концентраций веществ А и В, уравнение реакции А В является полным. Скорость реакции может также зависеть от фиксированной начальной или общей концентрации энзима, и тогда эта концентрация будет параметрической переменной. Но если скорость реакции зависит от мгновенной концентрации комплекса С или энзима Е, уравнение реакции Л —> i не будет полным. Можно предположить, что концентрация комплекса С всегда постоянна, Г и, таким образом, исключить ее из кинетического закона, выразив скорость реакции А В только через концентрации этих двух ве-. л ществ или одного из них. К сожалению, гипотезы подобного рода почти никогда не оправдываются в точности. Например, если в на-чальный момент в системе нет комплекса С, должно пройти некоторое время прежде чем будет достигнута его стационарная концентрация, которая хотя и не является строго постоянной, но сравнительно медленно меняется во времени. Б некоторых случаях период индукции бывает очень коротким, так что гипотеза о постоянстве концентрации комплекса С выполняется в течение почти всего периода реакции и выведенный с ее помощью кинетический закон находится в достаточно хорошем соответствии с экспериментальными данными. При необходимости уравнения таких реакций могут быть выделены в особый класс почти полных , но такое выделение вызывает возражения в теоретическом отношении, хотя и может оказаться практически полезным. [c.17]

    В соответствии с этим методом при достижении стационарного состояния скорости образования и расходования промежуточных продуктов реакции равны между собой, то есть в системе устанав — ливается стационарная концентрация промежуточных веществ. [c.101]

    II для ряда различных третьих частиц М. Это дает возможность рассчитать для ряда изученных систем значения 1а и Бенсон и Басс [20] сделали такие расчеты для ряда реакций бромирования. Кроме того, исходя из уравнения (XIII.6.И) и вводя упрощающие предположения, они рассчитали пороговые температуры для различных двухатомных молекул Ха- Это температуры, при которых за данное время достигается 90% стационарной концентрации радикалов. В табл. XIII.2 приведены значения и температуры, рассчитанные в предположении, что для всех молекул М = 1 атм, Ха = 20мм рт. ст., /с/х = 3-10 л /лоль -сек. Для других условий или для других значений констант обрыва величины могут быть рассчитаны на основании уравнения (X[II.6.11). [c.296]

    Применяя метод стационарного состояния (А, В ) < (А, В) и положив dA /di = = О, можно найти стационарные концентрации Л тац [c.205]

    Для того чтобы решить систему этих уравнений, можно пренебречь флуоресценцией и дезактивацией возбужденных молекул Вг2, так что удельная скорость реакции 1 = 2/а, где —среднее число фотонов, поглощенных 1 см в 1 сек. Удобно также допустить, что определенная доля атомов Вг, ударяющихся о стенку, захватывается стенкой, давая Вг2. В действительности же коэффициент рекомбинации на стенке должен, конечно, зависеть от стационарной концентрации атомов Вг, химической природы стенки, концентрации других примесей, которые могут влиять на абсорбцию атомов Вг, и т. д. [c.289]

    Здесь В — молекула, которая разлагается. В — возбужденная молекула. Стационарная концентрация В равна [c.202]

    Здесь константа ингибирования / <0,1 и скорость зависит от первой степени интенсивности света. При этом предполагается, что атомы С1 исчезают при диффузии (или конвекции) к стенкам по реакции первого порядка. Это более или менее хорошо согласуется с другими работами [30, 31] в этой области, хотя вследствие трудностей, возникающих при применении метода стационарных концентраций, все эти результаты должны быть приняты с некоторыми оговорками. Краггс [32], Алманд и Сквайр [32, 33] работали с очень низкими концентрациями На и показали, что зависимость от интенсивности света изменяется от при низких концентрациях С12 (- 0,01 мм рт. ст.) и низких интенсивностях света до 7 2 при больших концентрациях С1г( 450 мм рт. ст.) и больших интенсивностях света. При постоянной интенсивности света скорость проходит через максимум по мере изменения давления С12. На основании этого можно ожидать, что существуют два пути гибели атомов С1 в системе, сходные со случаем гибели атомов Вг [см. уравнение (XIII.4.4)]. Эти авторы предположили, что специфическое действие С1г как третьей частицы основано на образовании важного промежуточного соединения С1з. Тогда стадию обрыва цепи можно записать следующим образом  [c.301]

    Существует ряд особенностей цепной реакции Н2+ВГ2, которые представляют существенный интерес. Прежде всего обращает на себя внимание тот факт, что энергия распада молекулы Вгг равна 46 ккал, а энергия активации реакции составляет только 40 ккал. Другая особенность состоит в том, что стационарная концентрация атомов Н, получающаяся в результате реакции, во много раз больше, чем концентрация атомов, обычно наблю- [c.291]

    Можно показать, что при достаточно низких давлениях рекомбинация атомов брома будет происходить в основном на стенках, так что стационарная концентрация атомов Вг дается выражением (Вг)стац = 2A J (М) (Вг2)/йо- Учитывая, что ко не имеет анергии активации, для получения атомов брома необходимо затратить энергию 46 ккал, которая равна полной энергии связи. Однако данное предположение неверно, так ак в этом случае концентрация атомов Вг на стенке не является стационарной, т. е. стенку можно рассматривать как акцептор радикалов. [c.292]

    Метод стационарных концентраций требует, чтобы количество атомов Вг, покидающих стенку, было равно количеству атомов Вг, соударяющихся с ней, так что во всем сосуде устанавливается равновесие Вгг 2Вг. [c.292]

    Стационарное состояние в цепной реакции не достигается мгновенно. Для этого требуется определенное время, которое может быть рассчитано из кинетического механизма, если известны индивидуальные константы скорости для реакций обрыва и инициирования. Бенсон [19] рассчитал для гомогенной цепной системы, отвечающей случаю 1, время 4, необходимое для достижения некоторой доли а стационарной концентрации X, и долю реакции Ра, протекающей за это время. Для термического инициирования ta дается выражением [c.295]

    СТАЦИОНАРНОЙ КОНЦЕНТРАЦИИ АТОМОВ ДЛЯ НЕКОТОРЫХ ДВУХАТОМНЫХ МОЛЕКУЛ ПРИ ГОМОГЕННЫХ ПРОЦЕССАХ (Температура дана с точностью до 5% °К) [c.296]

    ВРЕМЯ (СВК) ДОСТИЖЕНИЯ 90% СТАЦИОНАРНОЙ КОНЦЕНТРАЦИИ АТОМОВ ДЛЯ ФОТОЛИЗА ПРИ РАЗЛИЧНЫХ АБСОЛЮТНЫХ ИНТЕНСИВНОСТЯХ СВЕТА [c.297]

    Выражение для стационарной концентрации СН3 имеет вид  [c.319]

    МетоА стационарных концентраций. Этот метод впервые был пре,, ложен Боденштейном и в дальнейшем развит Семеновым Н.Н. Б литературе по химической кинетике он известен как метод стационарных концентраций Боденштейна — Семенова. [c.101]

    Это довольно сложная кинетическая схема, в которую входят три радикальных промежуточных соединения и одно соединение, а именно кетен, которое может достигать стационарного значения. Так как предполагается, что деструкции радикалов осуществляются по второму порядку, то невозможно уравнение для стационарных концентраций записать в явном виде. Если положить, что скорость этой реакции равна ф/ 1—х), а скорость реакции 2 равна ф/аЗ , где ф — часть возбужденных молекул ацетона, которая подвергается распаду, — среднее число квантов, поглощенных в 1 см за 1 сек, X — доля возбужденных молекул ацетона, которые распадаются по второму пути , тогда можно рассчитать отношение образования и деструк- [c.325]

    После этих приближений уравнение имеет явное решение для стационарных концентраций свободных радикалов  [c.326]

    Имеется еще очень мало доказательств за или против такого приближения, С точки зрения теории простых столкновений это приближение вполне приемлемо— оно не вносит значительной ошибки в расчет стационарных концентраций, [c.326]

    Используя модель упругого сферического соударения, можно вычислить частоту столкновения трех молекул А, В и С, рассчитав сначала стационарные концентрации бинарных комплексов АВ, ВС и СА. Если обозначить через Тдв, вс и Тса величины среднего времени жизни этих бинарных комплексов , то их стационарные концентрации ириближенно даются выражениями [c.271]

    В настоящее время разработано и применяется множество м< Тодов составления кинетических моделей гетерогенных каталитических реакций, среди которых наибольшей популярностью пс>льзуются следующие 1) метод, основанный на законе действующих поверхностей, и 2) метод стационарных концентраций. [c.98]

    Однако решения, данные для систем в разд. 111.7, указывают, что период индукции приблизительно в 4—10 раз больше. Другими словами, если стационарная концентрация Mi равна 1% от Ао, то примерно от 4 до 10% от Ло будет израсходовано прежде, чем Mi достигнет стационарной концентрации (см. рис. III.2 и III.3). Более детально о периоде индукции в цепных реакциях, в отношении которых были получены приведенные выше результат .), сказано в орипгпальной работе [26]. Если реакция осуществляется nyrt M цепи превращений, подобно реакции [c.55]

    И показал, что они согласуются (в пределах изменения концентрации в 100 раз) с наличием двух механизмов рекомбинации атомов брома. То, что рекомбинация атомов Вг действительно идет по двум механизмам, было непосредственно показано Рабиновичем и Вудом [15], которые также нашли, что ожидаемый максимум стационарной концентрации атомов брома [см. уравнение (XIII.4.И)] имеет место в области 200 мм рт. ст., когда Не играет роль третьего тела. Они предположили, что в этой системе конвекция может играть важную роль. [c.291]

    Когда происходит химическая реакция, это распределение нарушается реакцией, и в общем можно ожидать, что стационарная концентрация возбужденных молекул будет ниже, чем при равновесии. Лиидеман [13] первым предложил схему, которая позволяет оценить влияние реакции на это распределение. Его схема включает конкуренцию двух путей исчезновения возбужденных молекул — химической реакции и дезактивации при столкновении  [c.202]

    Если подставить из уравнения (XIII.2.7) стационарную концентрации атомов Н, то, пренебрегая ингибированием НВг. [c.287]

    Реакция 10 быстрее, чем реакция СН3 с ацетоном [46, 47] и, таким образом, заметно уменьшает стационарную концентрацию СН3, приводя одновременно к замене радикалов СНд очень активными атомами I. Если большая часть радикалов реагирует по реакции 10, за которой следует очень быстрая реакция 11, то распад каждой молекулы ди-/и/)е г-бутилперекиси (реакция 1) приводит к образованию двух молекул СН4, двух молекул ацетона и двух дибутилгидроперекисных радикалов или к увеличению скорости в 3 раза. Дальнейшее повышение концентрации H I приводит к тому, что реакция 8 становится более быстрой, чем реакция 1. Отмечено, что НВг не оказывает влияния на скорость разложения перекиси. Это объясняется относительной инертностью атомов Вг, которые вступают в реакцию отрыва атома Н намного медленнее, чем СНд. [c.323]

    Если исходить из этих предположений, то метод стационарных концентраций дает для стационарной концентрации атомов Н тот же самый результат, как и прежде [уравнение (XIII.2.7)]  [c.289]

    Оказывается, что по мере увеличения сложности молекулы КН энергия связи Х)(БН) уменьшается и стационарная концентрация К увеличивается по сравнению с концентрацией Вг. Но одновременно с этим изменением уменьшается и , а следовательно, возрастает скорость реакции и увеличивается длина цепи Ф. Более того, обрыв по реакциям К + К и К + X становится более важным но сравнению с обрывом X + X. Однако полученные данные, которые относятся к этану, изобутану, неоиентану и толуолу, не согласуются между собой и, вероятно, малонадежны. [c.298]

    Пренебрегая в данном случае знаменателями, которые учитывают ингибирование, можно в этих выражениях представить числители как произведения двух множителей, причем первый отвечает соответственно стационарной концентрации атомов Вг(ЛГ,,2Вг2) 2 и IJk2Ш) , а второй — суммарной скорости образования НВг относительно удельной концентрации атомов брома. В ценных реакциях, которые до сих пор рассматривались, цикл состоял только из двух стадий одной быстрой и одной медленной. В выражение для суммарной скорости входит лишь константа кз, отвечающая медленной цепной стадии. Этой стадией является отрыв атома водорода Вг — — КН Л- НВг -Ь К. Для термической реакции суммарная константа скорости /сг= кзК (1 равна произведению константы скорости бимолекулярной реакции кз и константы равновесия1,2- Их энергия активации, которая является эксперименталь- [c.298]

    Используя метод стационарных концентраций для (Н), (СНд) и (С0Н5), находим [c.310]

    В этом случае уравнения сложной цепной реакции могут быть обработаны по методу стационарных концентраций. Общая концентрация всех радикалов в системе представляет собой сумму (Н) + (СНз) + (С2Нз). Так как реакции продолжения цепи просто приводят к замене одного радикала другим, но не изменяют общей концентрации радикалов, можно для стационарного состояния всех радикалов приравнять сумму всех скоростей реакций инициирования сумме всех скоростей реакции обрыва. Это приводит к уравнению  [c.316]

    Исходя из этой схемы, можно рассчитать стационарные концентрации различ-. ных промежуточных радикалов. Эти концентрации будут равны []щ-трет-бутилперекись сокращенно обозначается с11ВР) [c.319]

    Из всех доказательств ясно видно, что разложение ди-/ г/>е/ г-бутилпере-киси при температурах выше 100° может рассматриваться как источник получения относительно больших и контролируемых стационарных концентраций радикалов СН3. Пиролиз ди-да/)е г-бутилперекиси будет не чувствителен к любым вторичным реакциям в системе до тех пор, пока ни одна из этих реакций не приведет к образованию радикалов или атомов более активных, чем радикал СН-,. При этпх условиях система является наиболее пригодной для изучения реакций радикалов СНд. До сих пор ди- г/)е/и-бутилпере-кись использовалась для изучения реакций в растворах. Однако, если ввести в схему цепной реакции некоторые дополнительные стадии, эта система с успехом может быть применена для изучения элементарных реакций радикалов в газовой фазе .  [c.323]

    Во время опыта интенсивность света и концентрация ацетона остаются практически постоянными. Стационарные концентрации радикалов также будут постоянны, и, следовательно, уравнение (XIII,13.8) можно проинтегрировать. В результате приходим к следующему выражению для количества этана и метана, образующихся в реакции за время Г. [c.326]

Курс химической кинетики (1984) — [

c.215

]

Курс физической химии Издание 3 (1975) — [

c.676

]

Физическая химия Книга 2 (1962) — [

c.207

]

Курс химической кинетики (1962) — [

c.229

]