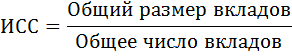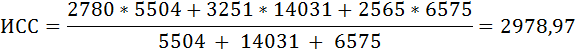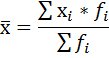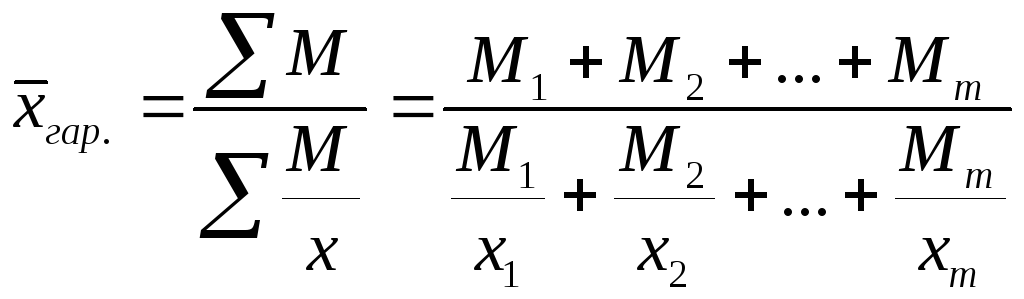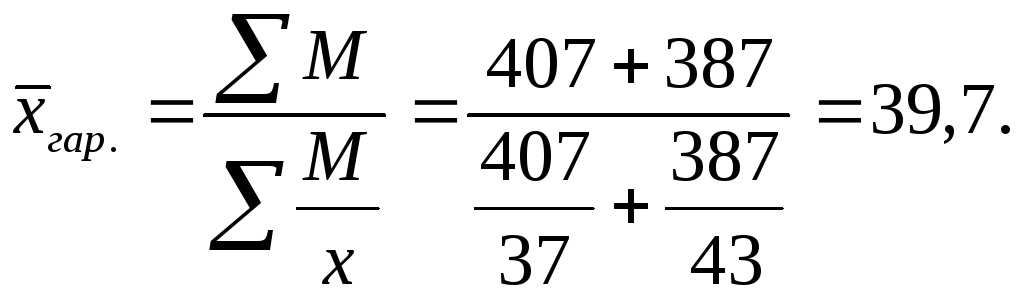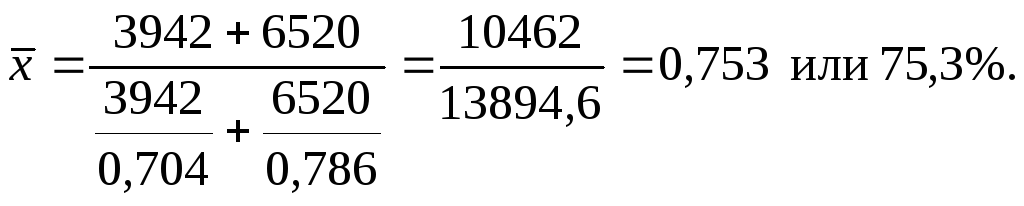По трём районам города имеются следующие данные (на конец года):
| Район | Число отделений Сбербанка | Среднее число вкладов в отделении | Средний размер вклада в рублях |
| 1 | 4 | 1376 | 2780 |
| 2 | 9 | 1559 | 3251 |
| 3 | 5 | 1315 | 2565 |
Определите средний размер вклада в Сбербанке в целом по городу.
Решение:
Для определения среднего размера вклада в Сбербанке используем исходное соотношение средней (ИСС):
Определим общее число вкладов, умножив число отделений на среднее число вкладов в отделении:
4*1376 + 9*1559 + 5*1315 = 5504 + 14031 + 6575 = 26110
Из исходного соотношения среднего видно, что общий размер вкладов равен произведению среднего размера вклада и общего числа вкладов:
Общий размер вкладов = 2780*5504+3251*14031+2565*6575
Тогда средний размер вклада в Сбербанке будет равен:
А это есть ни что иное, как расчёт по формуле средней арифметической взвешенной:
где
хi – i-й вариант осредняемого признака,
fi – вес i-го варианта.
Информация о вкладах в банке для расчета средних значений
|
Октябрь |
Ноябрь |
|||
|
Вид |
Число f |
Средний тыс. х |
Сумма млн. М |
Средний размер вклада, тыс. х |
|
До |
10 |
35 |
4,07 |
37 |
|
Срочный |
8 |
40 |
3,87 |
43 |
В
октябре известен средний размер вкладов
каждого вида х
и количество вкладов f.
Следовательно, для расчета среднего
размера вклада по двум видам применяем
формулу средней арифметической
взвешенной, тыс. руб.:
В ноябре известен средний размер вкладов
каждого вида, а количество вкладов не
известно, но зато имеются данные об
общих суммах вкладов.
Путем
деления сумм вкладов М каждого вида на
их средний размер вклада х
можно определить веса – число вкладов
по их видам f,
а затем определить средний размер вклада
по двум видам по формуле средней
арифметической.
Однако,
если в расчете использовать среднюю
гармоническую, то отпадает необходимость
предварительного расчета весов –
размеров вкладов по каждому виду,
поскольку эта операция заложена в саму
формулу. Средняя гармоническая взвешенная
применяется, когда статистическая
информация не содержит частот f
по отдельным единицам совокупности, а
представлена как произведение xf.
Чтобы исчислить среднюю, обозначим
xf=М,
откуда f=w/x. Преобразуем формулу средней
арифметической так, чтобы по имеющимся
данным x
и М можно было исчислить среднюю.
В
формулу средней арифметической взвешенной
вместо xf
подставим
М, вместо f
– отношение М/x
и получим формулу средней гармонической
взвешенной:
Итак, средний
размер вклада в ноябре по двум их видам
находим по формуле средней гармонической
взвешенной, тыс. руб.:
Пример
5. В результате
проверки двух партий муки потребителям
установлено, что в первой партии муки
высшего сорта было 3942 кг., что составляет
70,4% общего веса муки этой партии. Во
второй партии муки высшего сорта было
6520 кг., что составляет 78,6% общего веса
муки этой партии. Определите процент
муки высшего сорта в среднем по первой
и второй партиям вместе.
Решение
Средний процент
муки высшего сорта по двум партиям
определяем по формуле средней гармонической
взвешенной:
Средняя геометрическая
Пример
1.
Предположим, Вы внесли деньги в банк на
срочный депозит, процент по которому
ежегодно изменяется в зависимости от
ставки рефинансирования ЦБ. После
каждого года сумма, равная процентному
приросту, добавляется к сумме счета.
Например, первоначальная сумма вклада
составила 100 денежных единиц. За первый
Вы получили 5% дохода по вкладу, за второй
7%, за третий 9% и за 4-й – 10%. Каков средний
уровень дохода по вкладу за 4 года?
Можно
сложить вычислить среднюю арифметическую
величину дохода:.
Верно ли это?
Ведем
следующие условные обозначения: P
– первоначальная сумма вклада,
— доход по вкладу в первый, второй, третий
и четвертый годы соответственно (в долях
единиц), F – сумма вклада по истечении
четырех лет.
Если
первоначальная сумма вклада — Р,
то после первого года она возрастает и
становится
.
В конце второго года эта сумма составит
.
В конце третьего года:.
По истечении четырех лет сумма составит
Если
необходимо определить средний процент
дохода i,
который даст сумму дохода F
по истечении четырех лет, при прибавлении
ежегодного накопленного прироста к
сумме вклада, то это будет величина,
которая определится из следующего
уравнения:
Решение этого
уравнения находится по формуле:
,
где (i+1)
— геометрическая средняя из (1+i1
),(1+i2),(1+i3),(1+i4)).
Средний
процент дохода по вкладу равен
,
что отличается от результата, полученного
по средней арифметической.
Общий вид формулы средней геометрической
невзвешенной:
Средней геометрической взвешенной:
(5.12)
Согласно правилу
мажорантности средней, расчет по средней
арифметической завышает результат, чем
длиннее период расчета, тем больше будет
ошибка.
Пример 2. В результате инфляции за
первый год цена товара возросла в два
раза к предыдущему году, а за второй год
еще в три раза к уровню предыдущего
года. Ясно, что за два года цена возросла
в 6 раз. Каков средний темп роста цены
за год? Арифметическая средняя здесь
непригодна, поскольку, если за год цена
выросла бы в (2+3)/2=2,5 раза, то за два года
цена выросла бы в 2,5 *2,5 = 6,25, а не в 6 раз.
Геометрическая средняя даст правильный
ответ:раза.
Геометрическая
средняя дает наиболее правильный по
содержанию результат осреднения, если
задача состоит в нахождении такого
значения признака, который качественно
был бы равно удален как от максимального,
так и от минимального значения признака.
Пример
3. Максимальный
выигрыш в лотерее составляет миллион
рублей, а минимальный – сто рублей.
Какую величину можно считать средней
между миллионом и сотней? Арифметическая
средняя явно непригодна, так как
составляет 500050 рублей, а это, как и
миллион, крупный, а никак не средний
выигрыш. Геометрическая средняя в этом
случае дает наиболее правильный с точки
зрения экономики и логики ответ:
руб.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
По трем филиалам банка имеются данные: Рассчитайте средний размер вклада за каждый месяц и в целом за четыре месяца.






Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
По трем филиалам банка имеются данные:
|
Филиалы |
Январь |
Февраль |
Март |
Апрель |
||||
|
Ср. размер вклада, тыс. руб. |
Общая сумма вкладов, тыс.руб. |
Ср. размер вклада, тыс. руб. |
Число вкладов |
Ср. размер вклада, тыс. руб. |
Доля в общей сумме вкладов банка, % |
Ср. размер вклада, тыс. руб. |
Доля в числе вкладчиков, % |
|
|
1 |
36 |
500 |
45 |
70 |
43 |
43 |
45 |
25 |
|
2 |
25 |
700 |
37 |
90 |
23 |
46 |
36 |
40 |
|
3 |
50 |
1000 |
62 |
100 |
55 |
11 |
58 |
30 |
Рассчитайте средний размер вклада за каждый месяц и в целом за четыре месяца.
Решение:
1. Вычислим средний размер вклада за январь по формуле средней гармонической взвешенной:
где S – общая сумма вкладов;
s – средний размер вклада.
Средний размер вклада за январь составил 35,5 тыс.руб.
2. Средний размер вклада за февраль найдем по формуле средней арифметической взвешенной:
где f – число вкладов.
- Сравните показатели вариации заработной платы по двум бригадам. Найдите общую дисперсию заработной платы по цеху.
- По сельскохозяйственным производственным кооперативам (СХПК) района имеются следующие данные. Сгруппируйте кооперативы в три группы с равными интервалами по площади посева зерновых.
- Рост цен на молоко в первом квартале 2010 года по РФ характеризуется следующими данными: Определить общее изменение цен на молоко за данный период.
- По двум трикотажным фабрикам производственного объединения имеются следующие данные о количестве и качестве произведенной продукции: Вычислите: 1) объем всей произведенной продукции.
Для анализа динамики среднего размера вклада и его структуры широко применяется система индексов.
Рассмотрим методику расчета индексов среднего размера вклада переменного и постоянного состава и индекса влияния структуры.
Обозначим сумму вкладов буквой В, количество вкладов — N, средний размер вклада — i.
Формула расчета среднего размера вклада по совокупности представляется следующим выражением:
(2.4.1),
или формулой средней арифметической взвешенной:
(2.4.2).
Индекс среднего размера вклада переменного состава:
(2.4.3),
где i- средний размер вклада;
d- количество вкладов.
Индекс среднего размера вклада постоянного состава:
(2.4.4).
Индекс влияния структуры:
(2.4.5).
Абсолютный прирост среднего размера вклада:
(2.4.6),
в том числе за счет изменения:
а) индивидуальных уровней вкладов по социальным группам:
(2.4.7),
б) удельного веса числа вкладов с различным уровнем вклада:
(2.4.8) [7, с.401].
На основе предложенных нами формул (2.4.1 — 2.4.8) и исходных данных (Приложения Т) произведем расчеты показателей среднего размера вклада и проанализируем его динамику и структуру за 2005 — 2007гг.
Рассчитаем средний размер вклада в 2005 — 2007гг по формуле (2.4.1):
Сравнивая полученные нами результаты, можно сделать вывод о том, что в 2005-2006гг. средний размер вклада был примерно одинаковым, но стоит отметить, что в 2006г. общая сумма вкладов увеличилась на 29,15% по сравнению с 2005г. Кроме того, увеличилось и количество самих вкладов на 126590749 штук. В 2007г. средний размер вклада составил 4023 рубля, что значительно больше, чем в 2005-2006гг. Подобное увеличение связано с тем, что в 2007г. заметно увеличилось общая сумма и количество вкладов.
Рассчитаем индекс среднего размера вклада переменного состава по формуле (2.4.3):

Индекс среднего размера вклада постоянного состава рассчитаем по формуле (2.4.4):
Анализируя полученные данные, можно проследить следующую тенденцию: при уменьшении размера вклада в 2006г. по сравнению с 2005г. на 3,4347764 рубля средний размер вклада уменьшился на 0,1132%, а в 2007г. по сравнению с 2006г. средний размера вклада увеличился в 1,3266555 раза или на 32,66555%. В 2005г. средний размер вклада был на 32,5344% меньше, чем в 2007г., что в абсолютном выражении составило 987,565 рублей.
Расчет индекса влияния структуры произведем по формуле (2.4.5):
Из полученных результатов следует то, что при увеличение количества вкладов в 2006г. по сравнению с 2005г. на 126590749 и неизменной величине вклада, средний размер вклада увеличивается на 29,68%, В 2007г. количество вкладов превышает 2006 на 131605987, средний размер вклада увеличивается на 23,81% ,а по отношению к 2005г. на 60,54%.
Абсолютный прирост среднего размера вклада за счет изменения индивидуальных уровней вкладов вычислим по формуле (2.4.7):
Абсолютный прирост среднего размера вклада за счет изменения удельного веса числа вкладов с различным уровнем вклада вычислим по формуле (2.4.8):
Таким образом абсолютный прирост среднего размера вклада за 2005-2007 гг. за счет изменения индивидуальных уровней вкладов и удельного веса числа вкладов с различным уровнем вклада составил (2.4.6):
Следовательно, наибольший прирост среднего размера вклада за период с 2005 по 2007гг. наблюдался в 2007г. и составил 35,48% от прироста 2006г.

первая задача:
В массив внесены суммы вкладов вкладчиков, которые зашифрованы номерами. Найти среднюю сумму вкладов. Определить сколько вкладчиков имеют вклады выше средней суммы
вторая:
В массиве y(25), сформированном случайным образом, найти среднее геометрическое модулей всех ненулевых элементов
третья:
В массив внесен годовой баланс предприятия. Найти среднее значение суммы баланса за год. Определить, в какие месяцы (по номерам) баланс был меньше средней величины.
четвертая:
В массиве b(40), сформированном случайным образом, найти количество элементов, стоящих на нечетных местах, удовлетворяющих условию d < bi < t , где d и t – заданные числа
пятая:
В массиве содержится сумма заработной платы работающих в цехе по порядку их номеров в ведомости (их всего 20). Найти среднюю заработную плату. Определить сколько работающих получают больше средней заработной платы, а сколько меньше.
шестая:
Сложить две матрицы a (7, 3) и b (7, 3) и найти наибольший элемент в полученной сумме