Как найти среднюю силу импульса - Avtoru.top - решение различных проблем

Как определить среднюю силу

Средняя сила – это условная величина. В случаях, когда сила, действующая на тело, меняется со временем или действие силы очень мало, то определить величину силы в каждый момент времени не представляется возможным. Поэтому в данных случаях принимают допущение, что за определенное время на тело действовала постоянная сила равная средней и рассчитывают именно ее — Fср.

Вам понадобится

умение интегрировать

Инструкция

Пусть тело под действием некой силы F изменило свою скорость с V1 до V2 за короткий промежуток времени Δt. Ускорение данного тела будет равно a=(V2-V1)/Δt, где а, V1 и V2 – являются векторными величинами.

Подставьте данное выражение в формулу второго закона Ньютона: F=ma=m(V2-V1)/Δt=(mV2-mV1)/Δt, не забывая, что сила F – тоже векторная величина.

Запишите полученную формулу в несколько ином виде: FΔt=mΔV =Δp. Векторную величину FΔt, равную произведению силы на время ее воздействия, называют импульсом силы и измеряют в ньютонах умноженных на секунду (Н•с). А произведение массы тела на его скорость p=mV – импульсом тела или количеством движения тела. Эту векторную величину измеряют в килограммах, умноженных на метр в секунду (кг•м/с).

Т.о. второй закон Ньютона можно сформулировать иначе: импульс силы, действующей на тело равен изменению импульса тела: FΔt=Δp.

Если время воздействия силы было очень мало, например, во время удара, то среднюю силу находят так: Fср=Δp/Δt=m(V2-V1)/Δt.Пример: Мяч массой 0,26кг летел со скоростью 10м/с. После удара волейболиста, мяч увеличил скорость до 20м/с. Время удара – 0,005с. Средняя сила воздействия руки волейболиста на мяч равна в данном случае Fср=0,26•(20-10)/0,005с=520Н.

Если сила, действующая на тело, не постоянна, а меняется со временем по закону F(t), то путем интегрирования функции F(t) по времени t на промежутке от 0 до T найдите изменение импульса тела: dр=F(t)dt.

И по формуле Fср=dp/dt определите значение средней силы.Пример: Сила меняется со временем по линейному закону F=30t+2. Найдите среднюю силу воздействия за 5с. Сначала вычисляем импульс тела p=∫(30t+2)dt=15t²+2t , а затем среднюю силу: Fср=(15t²+2t)/t=15t+2=15•5+2=77Н

Видео по теме

Обратите внимание

Сила является векторной величиной. Если в результате расчетов значение Fср получилось отрицательным, это значит, что вектор силы направлен в сторону, противоположную направлению координатной оси.

Полезный совет

Не забывайте при решении задач переводить все используемые в формулах величины в СИ. Т.е. массу – в килограммы, скорость – в метры, деленные на секунду, а силу – в ньютоны.

Источники:

Физика для углубленного изучения, Е.И. Бутиков, А.С. Кондратьев

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Как определить среднюю силу

Т.о. второй закон Ньютона можно сформулировать иначе: импульс силы, действующейна тело равен изменению импульса тела: FΔt=Δp.

И по формуле Fср=dp/dt определите значение средней силы.Пример: Сила меняется со временем по линейному закону F=30t+2. Найдите среднюю силу воздействия за 5с.Сначала вычисляем импульс тела p=∫(30t+2)dt=15t²+2t , а затем среднюю силу: Fср=(15t²+2t)/t=15t+2=15•5+2=77Н

Источник

Импульс

Второй закон Ньютона в импульсной форме
Пример вычисления силы
Импульс системы тел
Закон сохранения импульса
Закон сохранения проекции импульса

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: импульс тела, импульс системы тел, закон сохранения импульса.

Импульс тела — это векторная величина, равная произведению массы тела на его скорость:

Специальных единиц измерения импульса нет. Размерность импульса — это просто произведение размерности массы на размерность скорости:

$[p]=[m]cdot [upsilon ]= frac{displaystyle kgcdot m}{displaystyle c}$ .

Почему понятие импульса является интересным? Оказывается, с его помощью можно придать второму закону Ньютона несколько иную, также чрезвычайно полезную форму.

к оглавлению ▴

Второй закон Ньютона в импульсной форме

Пусть vec{F} — равнодействующая сил, приложенных к телу массы . Начинаем с обычной записи второго закона Ньютона:

С учётом того, что ускорение тела vec{a} равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:

$mfrac{displaystyle dvec{upsilon } }displaystyle {dt}=vec{F}$ .

Вносим константу под знак производной:

$frac{displaystyle d(mvec{upsilon } )}{displaystyle dt}= vec{F}$ .

Как видим, в левой части получилась производная импульса:

$frac{displaystyle dvec{displaystyle p} }{displaystyle dt}= vec{F}$ . ( 1)

Соотношение ( 1) и есть новая форма записи второго закона Ньютона.

Второй закон Ньютона в импульсной форме. Производная импульса тела есть равнодействующая приложенных к телу сил.

Можно сказать и так: результирующая сила, действующая на тело, равна скорости изменения импульса тела.

Производную в формуле ( 1) можно заменить на отношение конечных приращений:

$frac{displaystyle Delta vec{displaystyle p} }{Delta displaystyle t}= vec{displaystyle F}$ . ( 2)

В этом случае vec{F} есть средняя сила, действующая на тело в течение интервала времени Delta t . Чем меньше величина Delta t , тем ближе отношение к производной , и тем ближе средняя сила vec{F} к своему мгновенному значению в данный момент времени.

В задачах, как правило, интервал времени Delta t достаточно мал. Например, это может быть время соударения мяча со стенкой, и тогда vec{F} — средняя сила, действующая на мяч со стороны стенки во время удара.

Вектор в левой части соотношения ( 2) называется изменением импульса за время Delta t . Изменение импульса — это разность конечного и начального векторов импульса. А именно, если $vec{p} _{0}$ — импульс тела в некоторый начальный момент времени, vec{p} — импульс тела спустя промежуток времени Delta t , то изменение импульса есть разность:

$Delta vec{p} = vec{p} -vec{p} _{0}$ .

Подчеркнём ещё раз, что изменение импульса — это разность векторов (рис. 1):

Рис. 1. Изменение импульса

Пусть, например, мяч летит перпендикулярно стенке (импульс перед ударом равен $vec{p} _{0}$ ) и отскакивает назад без потери скорости (импульс после удара равен $vec{p}= -vec{p} _{0}$ ). Несмотря на то, что импульс по модулю не изменился ( $p= p _{0}$ ), изменение импульса имеется:

$Delta vec{p} = vec{p} -vec{p} _{0}= -vec{p} _{0}-vec{p} _{0}= -2vec{p} _{0}$ .

Геометрически эта ситуация показана на рис. 2:

Рис. 2. Изменение импульса при отскоке назад

Модуль изменения импульса, как видим, равен удвоенному модулю начального импульса мяча: $Delta p= 2p_{0}$ .

Перепишем формулу ( 2) следующим образом:

, ( 3)

или, расписывая изменение импульса, как и выше:

$vec{p} -vec{p} _{0}=vec{F} Delta t$ .

Величина называется импульсом силы. Специальной единицы измерения для импульса силы нет; размерность импульса силы равна просто произведению размерностей силы и времени:

(Обратите внимание, что Hcdot c оказывается ещё одной возможной единицей измерения импульса тела.)

Словесная формулировка равенства ( 3) такова: изменение импульса тела равно импульсу действующей на тело силы за данный промежуток времени. Это, разумеется, снова есть второй закон Ньютона в импульсной форме.

к оглавлению ▴

Пример вычисления силы

В качестве примера применения второго закона Ньютона в импульсной форме давайте рассмотрим следующую задачу.

Задача. Шарик массы m= 100 г, летящий горизонтально со скоростью м/с, ударяется о гладкую вертикальную стену и отскакивает от неё без потери скорости. Угол падения шарика (то есть угол между направлением движения шарика и перпендикуляром к стене) равен $alpha = 60^{circ}$ . Удар длится с. Найти среднюю силу,
действующую на шарик во время удара.

Решение. Покажем прежде всего, что угол отражения равен углу падения, то есть шарик отскочит от стены под тем же углом alpha (рис. 3).

Рис. 3. К задаче (вид сверху)

Тут всё дело в том, что стена — гладкая. Это значит, что трения между шариком и стеной нет. Следовательно, со стороны стены на шарик действует единственная сила vec{N} — сила упругости, направленная перпендикулярно стене (рис. 4).

Рис. 4. К задаче

Согласно ( 3) имеем: . Отсюда следует, что вектор изменения импульса сонаправлен с вектором vec{N} , то есть направлен перпендикулярно стене в сторону отскока шарика (рис. 5).

Рис. 5. К задаче

Векторы $vec{p} _{0}$ и
vec{p} равны по модулю
(так как скорость шарика не изменилась). Поэтому треугольник, составленный из векторов $vec{p} _{0}$ , vec{p} и , является равнобедренным. Значит, угол между векторами vec{p} и равен alpha , то есть угол отражения действительно равен углу падения.

Теперь заметим вдобавок, что в нашем равнобедренном треугольнике есть угол $60^{circ}$ (это угол падения); стало быть, данный треугольник — равносторонний. Отсюда:

$Delta p= p_{0}= mupsilon = 0,1cdot 6= 0,6~Hcdot c$ .

И тогда искомая средняя сила, действующая на шарик:

$N= frac{displaystyle Delta p}{displaystyle Delta t}= frac{displaystyle 0,6}{displaystyle 0,01}= 60~H$ .

к оглавлению ▴

Импульс системы тел

Начнём с простой ситуации системы двух тел. А именно, пусть имеются тело 1 и тело 2 с импульсами $vec{p} _{1}$ и $vec{p} _{2}$ соответственно. Импульс vec{p} системы данных тел — это векторная сумма импульсов каждого тела:

$vec{p} = vec{p} _{1}+vec{p} _{2}$ .

Оказывается, для импульса системы тел имеется формула, аналогичная второму закону Ньютона в виде ( 1). Давайте выведем эту формулу.

Все остальные объекты, с которыми взаимодействуют рассматриваемые нами тела 1 и 2, мы будем называть внешними телами. Силы, с которыми внешние тела действуют на тела 1 и 2, называем внешними силами. Пусть $vec{F} _{1}$ — результирующая внешняя сила, действующая на тело 1. Аналогично $vec{F} _{2}$ — результирующая внешняя сила, действующая на тело 2 (рис. 6).

Рис. 6. Система двух тел

Кроме того, тела 1 и 2 могут взаимодействовать друг с другом. Пусть тело 2 действует на тело 1 с силой vec{T} . Тогда тело 1 действует на тело 2 с силой . По третьему закону Ньютона силы vec{T} и равны по модулю и противоположны по направлению: . Силы vec{T} и — это внутренние силы, действующие в системе.

Запишем для каждого тела 1 и 2 второй закон Ньютона в форме ( 1):

$frac{displaystyle dvec{displaystyle p} _ {displaystyle 1}}{displaystyle dt}=vec{F} _{1}+vec{T}$ , ( 4)

$frac{displaystyle dvec{displaystyle p} _{displaystyle 2}}{displaystyle dt}=vec{F} _{2}+{vec{T}}$ . ( 5)

Сложим равенства ( 4) и ( 5):

$frac{displaystyle dvec{displaystyle p} _{displaystyle 1}}{displaystyle dt}+frac{displaystyle dvec{displaystyle p} _{displaystyle 2}}{displaystyle dt}= vec{F} _{1}+vec{F} _{2}+vec{T} +{vec{T}}$ .

В левой части полученного равенства стоит сумма производных, равная производной суммы векторов $vec{p} _{1}$ и $vec{p} _{2}$ . В правой части имеем в силу третьего закона Ньютона:

$frac{displaystyle d(vec{displaystyle p} _{displaystyle 1}+vec{displaystyle p} _{displaystyle 2})}{displaystyle dt}= vec{F} _{1}+vec{F} _{2}$ .

Но $vec{p} _{1}+vec{p} _{2}= vec{p}$ — это импульс системы тел 1 и 2. Обозначим также $vec{F} _{1}+vec{F} _{2}= vec{F} _{external}$ — это результирующая внешних сил, действующих на систему. Получаем:

$frac{dvec{displaystyle p} }{displaystyle dt}= vec{F} _{external}$ . ( 6)

Таким образом, скорость изменения импульса системы тел есть равнодействующая внешних сил, приложенных к системе. Равенство ( 6), играющее роль второго закона Ньютона для системы тел, мы и хотели получить.

Формула ( 6) была выведена для случая двух тел. Теперь обобщим наши рассуждения на случай произвольного количества тел в системе.

Импульсом системы тел тел называется векторная сумма импульсов всех тел, входящих в систему. Если система состоит из тел, то импульс этой системы равен:

$vec{p} = vec{p} _{1}+vec{p} _{2}+...+vec{p} _{N}$ .

Дальше всё делается совершенно так же, как и выше (только технически это выглядит несколько сложнее). Если для каждого тела записать равенства, аналогичные ( 4) и ( 5), а затем все эти равенства сложить, то в левой части мы снова получим производную импульса системы, а в правой части останется лишь сумма внешних сил (внутренние силы, попарно складываясь, дадут нуль ввиду третьего закона Ньютона). Поэтому равенство ( 6) останется справедливым и в общем случае.

к оглавлению ▴

Закон сохранения импульса

Система тел называется замкнутой, если действия внешних тел на тела данной системы или пренебрежимо малы, или компенсируют друг друга. Таким образом, в случае замкнутой системы тел существенно лишь взаимодействие этих тел друг с другом, но не с какими-либо другими телами.

Равнодействующая внешних сил, приложенных к замкнутой системе, равна нулю: $vec{F} _{external}= vec{0}$ . В этом случае из ( 6) получаем:

$frac{displaystyle dvec{displaystyle p} }{displaystyle dt}= vec{0}$ .

Но если производная вектора обращается в нуль (скорость изменения вектора равна нулю), то сам вектор не меняется со временем:

Закон сохранения импульса. Импульс замкнутой системы тел остаётся постоянным с течением времени при любых взаимодействиях тел внутри данной системы.

Простейшие задачи на закон сохранения импульса решаются по стандартной схеме, которую мы сейчас покажем.

Задача. Тело массы $m_{1}= 800$ г движется со скоростью $upsilon _{1}= 3$ м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы $m_{2}= 200$ г со скоростью $upsilon _{2}= 13$ м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.

Решение. Ситуация изображена на рис. 7. Ось направим в сторону движения первого тела.

Рис. 7. К задаче

Поскольку поверхность гладкая, трения нет. Поскольку поверхность горизонтальная, а движение происходит вдоль неё, сила тяжести и реакция опоры уравновешивают друг друга:

$m_{1}vec{g} +vec{N} _{1}= vec{0}$ ,
$m_{2}vec{g} +vec{N} _{2}= vec{0}$ .

Таким образом, векторная сумма сил, приложенных к системе данных тел, равна нулю. Это значит, что система тел замкнута. Стало быть, для неё выполняется закон сохранения импульса:

$vec{p} _{before~hitting}= vec{p} _{after~hitting}$ . ( 7)

Импульс системы до удара — это сумма импульсов тел:

$vec{p} _{before~hitting}= m_{1}vec{upsilon _{1}} +m_{2}vec{upsilon _{2}}$ .

После неупругого удара получилось одно тело массы $m_{1}+m_{2}$ , которое движется с искомой скоростью :

$vec{p} _{after~hitting}= (m_{1}+m_{2})vec{upsilon }$ .

Из закона сохранения импульса ( 7) имеем:

$m_{1}vec{upsilon _{1}} +m_{2}vec{upsilon _{2}} = (m_{1}+m_{2})vec{upsilon }$ .

Отсюда находим скорость тела, образовавшегося после удара:

$vec{upsilon} = frac{displaystyle m_{displaystyle 1}vec{displaystyle upsilon _{displaystyle 1}} +displaystyle m_{displaystyle 2}vec{displaystyle upsilon _{displaystyle 2}} }{displaystyle m_{displaystyle 1}+displaystyle m_{displaystyle 2}}$ .

Переходим к проекциям на ось :

$upsilon _{x}= frac{displaystyle m_{displaystyle 1}displaystyle upsilon _{displaystyle 1x}+displaystyle m_{displaystyle 2}upsilon _{displaystyle 2x}}{displaystyle m_{displaystyle 1}+displaystyle m_{displaystyle 2}}$ .

По условию имеем: $upsilon _{1x}= 3$ м/с, $upsilon _{2x}= -13$ м/с, так что

$upsilon _{x}= frac{displaystyle 0,8cdot 3-0,2cdot 13}{displaystyle 0,8+0,2}= -0,2frac{m}{c}$ .

Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси . Искомая скорость: м/с.

к оглавлению ▴

Закон сохранения проекции импульса

Часто в задачах встречается следующая ситуация. Система тел не является замкнутой (векторная сумма внешних сил, действующих на систему, не равна нулю), но существует такая ось , сумма проекций внешних сил на ось равна нулю в любой момент времени. Тогда можно сказать, что вдоль данной оси наша система тел ведёт себя как замкнутая, и проекция импульса системы на ось сохраняется.

Покажем это более строго. Спроектируем равенство ( 6) на ось :

$frac{displaystyle dp_{displaystyle x}}{displaystyle dt}= F_{external,x}$ .

Если проекция равнодействующей внешних сил обращается в нуль, $F_{external,x}= 0$ , то

$frac{displaystyle dp_{displaystyle x}}{displaystyle dt}= 0$ .

Следовательно, проекция $p_{x}$ есть константа:

$p_{x}= const$ .

Закон сохранения проекции импульса. Если проекция на ось суммы внешних сил, действующих на систему, равна нулю, то проекция $p_{x}$ импульса системы не меняется с течением времени.

Давайте посмотрим на примере конкретной задачи, как работает закон сохранения проекции импульса.

Задача. Мальчик массы , стоящий на коньках на гладком льду, бросает камень массы со скоростью upsilon под углом alpha к горизонту. Найти скорость , с которой мальчик откатывается назад после броска.

Решение. Ситуация схематически показана на рис. 8. Мальчик изображён прямогольником.

Рис. 8. К задаче

Импульс системы «мальчик + камень» не сохраняется. Это видно хотя бы из того, что после броска появляется вертикальная составляющая импульса системы (а именно, вертикальная составляющая импульса камня), которой до броска не было.

Стало быть, система, которую образуют мальчик и камень, не замкнута. Почему? Дело в том, что векторная сумма внешних сил не равна нулю во время броска. Величина больше, чем сумма Mg+mg , и за счёт этого превышения как раз и появляется вертикальная компонента импульса системы.

Однако внешние силы действуют только по вертикали (трения нет). Стало быть, сохраняется проекция импульса на горизонтальную ось . До броска эта проекция была равна нулю. Направляя ось в сторону броска (так что мальчик поехал в направлении отрицательной полуоси), получим:

$-Mu+mupsilon _{0}cos alpha = 0$ ,

откуда

$u=frac{mupsilon _{0}cos alpha }{M}$ .

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Импульс» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

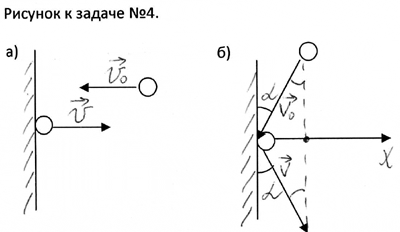
Определить среднюю силу удара

Изменение импульса тела равно
импульсу средней силы, действующей на
тело

Применяя эту формулу
для ударяемого шара массой
m₂,
получим (в проекциях на горизонтальную
ось)

где
— скорость шара после удара (до столкновения
шар находился в покое); <F>
— средняя сила удара; t
— длительность удара.

Определим

Подставив сюда вместо
выражение (4), получим расчетную формулу
для средней силы удара

,
(8)

где
l
— длина подвеса шара;
— угол, на который отклоняется второй
шар после удара.

Порядок выполнения работы

1. Провести корректировку осевой
установки шаров. Для этого шар, который
расположен выше, повернуть так, чтобы
риски на шарах находились на одном
уровне.

2. Установить
электромагнит на выбранном расстоянии
от начала шкалы и на такой высоте, чтобы
его ось была продолжением черты на шаре.

3. Включить прибор
в сеть. Нажать клавишу «СЕТЬ»
микросекундомера.

4. Отжать клавишу «ПУСК».

5. Правый шар
отклонить от положения равновесия на
угол
и удерживать его в этом положении
электромагнитом. Левый шар оставить в
состоянии покоя.

6. Нажать кнопку «СБРОС».

7. Нажать кнопку «ПУСК».

8. После столкновения
шаров отметить углы отклонения шаров
и.

9. Измерить
продолжительность столкновения шаров
t.

10. Опыт повторить
пять раз, выполняя пункты 4 — 9 при одном
и том же значении α₁.
Результаты измерений записать в табл.
1.

11. Отжать клавишу «СЕТЬ».

12. При помощи мерной
ленты определить длину l
подвески шаров (от точки подвеса до
центра тяжести шара).

Таблица 1

m₁ =	M₂ =	Δm =	l =	Δl =
α₁ =	Δα₁ =	Число измерений n =
i	1	2	…………..	n
α₁‘				<α₁‘>
α₂‘				<α₂‘>
τ				<τ>

13. Рассчитать
средние значения и погрешности измерений
величин
,,t
по формулам

где x
— измеряемая
величина, n
— число измерений, t(a,n)
— коэффициент Стьюдента. Учесть техническую
погрешность Δx_т.

14. По формулам
(2), (5), (6) и (7) определить импульсы шаров
,,идо и после столкновения, подставляя
средние значения углов отклонения <α₁‘>
и <α₂‘>.

15. Вычислить погрешности измерения
импульсов по формулам:

Углы необходимо
выражать в радианах; Dl
равно цене
деления

мерной ленты; Da₁
— цене деления шкалы.

16. Сравнить
полученные значения p_x
и p_x‘,
которые должны совпадать в пределах
ошибок измерений при выполнении
следующего неравенства:

(9)

17. Вычислить среднюю
силу удара по формуле (8), подставляя в
нее <α₂‘>
<τ>.

18. Вычислить погрешность измерения
силы удара по формуле

.
(10)

19. Результаты измерений записать в
табл. 2.

Таблица 2

<α₁‘> = , Δα₁‘ =	<α₁‘> = , Δα₂‘ =	<τ> = , Δτ =
p = , Δp =	p^‘ = , Δp^‘ =	Записать неравенство (9)
F =	ΔF =

Источник

Цели: Сформировать понятия импульса тела, импульса силы, изучить закон
изменения импульса тела, научить применять его для решения задач.

Этапы урока:

I. Повторение
Проверка домашнего задания.

II. Изучение нового материала
Рассказ учителя, беседа. Записи в тетрадь. Разбор жизненных ситуаций,
связанных с использованием понятия импульса тела

III. Закрепление
Решение задач. Устный опрос.

IV. Подведение итогов
Записать домашнее задание. Ответить на вопросы в учебнике.

V. Домашнее задание

Ход урока

I. Проверка выполнения домашнего задания

Учитель: Какие задания вызвали у вас наибольшее затруднение? Как вы
решали задачу №146? (задачник автор А.П.Рымкевич)

Ученик: Используя формулу кинематики a=(v-v₀)/t
нашли ускорение тела. Затем по II закону Ньютона
вычисляем силу F=ma.

Учитель: А кто решил эту задачу в общем виде? Запишите в тетрадь конечную
формулу.

Ученик: записывает на доске формулу F =
m (v-v₀)/t.

II. Изучение нового материала

Учитель: Преобразуем формулу из домашней задачи №146 к виду

. Мы получили
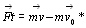
следствие из II Закона Ньютона. В правой части равенства
вы видите изменение величины, которая равна произведению m
на v. Эту величину называют ИМПУЛЬС ТЕЛА. Где же
используют это понятие?

Для решения задач механики используют законы динамики, в том случае, если
известна сила. Но в некоторых случаях силу найти очень сложно, например при
столкновениях тел. Например автомобилей, вагонов, бильярдных шаров. Возникают
силы упругости при очень сложных деформациях, да и время действия этих сил
слишком мало. Оценить эти силы можно с помощью уравнения*, используя понятие
импульса тела.

Записываем тему урока.

Записать под диктовку:

Произведение массы тела на его скорость называют импульсом тела и обозначают
импульс тела, величина
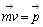
векторная. Направлен в сторону скорости тела измеряется импульс тела в кг м/с.

начальный импульс;
D–
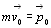
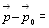
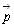
изменение импульса тела.
∆

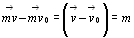
В левой части равенства получилась величина, равная произведению силы на
время ее действия 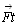– импульс
силы, величина векторная, направлен в сторону действия силы, измеряется в Н·с.

Формула * – закон изменения импульса тела. Кто сможет его сформулировать?

Ученик: Импульс силы равен изменению импульса тела.
= ∆,
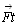
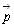
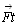
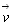
или = m∆.

(Ученики записывают в тетрадь.)

III. Закрепление

Учитель: Столкновения играют важную роль в природе: бомбардировка стенок
сосуда молекулами газа, рассеяние частиц на ядрах атомов, а также в жизни
человека. Как научиться управлять ими и обеспечить безопасность себе и своим
близким?

При столкновении тел происходим обмен импульсами, перераспределение импульса
между взаимодействующими телами. По изменению импульса тела можно судить о
средней силе, действующие на тело в процессе удара.

Применим закон изменения импульса к задачам о столкновениях, сопровождающих
человека.

(тексты заданий выданы перед уроком, дети читают отрывки из научных текстов с
последующим их обсуждением)

Задание 1.
Например , прыжки можно рассматривать как столкновения человека с опорой
(землей). В этот момент за короткое время происходит значительное изменение его
импульса, причем развиваются огромные силы, способные причинить ущерб здоровью.
Рассмотрим прыжок , человека массой 70 кг с небольшой высоты (1,25м). Скорость в
процессе приземления изменяется всего на 5м/с, но это происходит примерно за
0,01 с, поэтому средняя сила взаимодействия с землей составляет? Сравните ее с
силой тяжести, действующей на этого человека.

Ученик (записывает краткое решение на доске и комментирует):
Среднюю силу взаимодействия с землей можно рассчитать, используя закон изменения
импульса: F_ср.=m_∆v/t,
F_ср.=(70кг·5м/с)/0,01с=35000Н=35кН. Сила
тяжести, действующая на человека массой 70кг равна всего 700Н, т.е. в 50раз
меньше.

Учитель: Чтобы уменьшить силу удара, опытные прыгуны увеличивают время
приземления в десятки раз. Для этого они сгибают ноги в коленях. Надевают мягкую
обувь, делают мягким место приземления, (насыпают песок, настилают маты). Чтобы
уменьшить силу удара при приеме мяча, вратари надевают особые перчатки и следят
за тем, чтобы их рука могла двигаться назад, удлиняя тем самым промежуток
времени, в течение которого мяч останавливается. Чтобы победить в состязании,
бегунам или пловцам необходимо приобрести как можно большую скорость уже во
время старта. В этом им также помогут знания теории удара. Пловец, например, во
время старта способен оттолкнуться от края бассейна с силой 2,5 кН.

Учитель: Проблема безопасности человека при столкновениях актуальна не
только для спортсменов и людей экстремальных профессий, но также для пешеходов
на дорогах и автолюбителей. Рассмотрим следующую задачу

Задание 2.
Автомобиль массой 1500кг, движущийся со скоростью 12м/с (43 км/ч), врезается
в стену и останавливается. Какова средняя сила удара? Время взаимодействия
автомобиля со стеной составляет 0,05с. А если скорость больше в 2 раза?

Ученик: Записывает краткое решение на доске и комментирует. Аналогично
предыдущей задаче среднюю силу удара найдем из закона изменения импульса тела.
F_ср.=m_∆v/t,
F_ср.=360кН. Если скорость автомобиля будет в
два раза больше, т.е. почти 90км/ч, то средняя сила удара будет уже 720кН.

Учитель: На пассажира массой 100 кг, пристегнутого ремнями безопасности,
приходится гораздо меньшая сила (24кН).

Задание 3.
Чтобы процесс столкновения был менее разрушительным для человека, корпус
автомобиля делают деформируемым. Для чего это делаю? Выберите правильный вариант
ответа.

Благодаря деформациям корпуса уменьшается масса автомобиля, что приводит
к уменьшению средней силы удара.
Благодаря деформациям корпуса уменьшается время взаимодействия, что
приводит к уменьшению средней силы удара.
Благодаря деформациям корпуса возрастает время взаимодействия, что уже
приводит к уменьшению средней силы удара.

Ученик: Правильный ответ № 3.

Учитель: Подумайте и скажите, как еще можно увеличить время действия силы
в момент аварии.

Ученик: Это время можно еще увеличить, если воспользоваться ремнями и
подушками безопасности.

Учитель: Теперь вы, надеюсь, не забудете пристегнуться, когда соберетесь
ехать в автомобиле.

Учитель: Рассмотрим теперь столкновения, происходящие в микромире.

Задание 4.
Молекула массой 4,65·10^-26кг ударяется и без потери скорости
отскакивает от стенки сосуда. Найдете импульс силы, полученный стенкой, если
молекула летит и отскакивает: а) перпендикулярно; б) * под углом 30° к стенке.
Скорость молекулы равна 600м/с. (*этот случай следует разобрать с сильными
учениками на дополнительных занятиях)

Обратите внимание на то, что при упругом соударении со стенкой молекула
отскакивает от нее под тем же углом, под которым летит к ней. При этом модуль
скорости молекулы остается без изменения v=v₀.

Ученик: К этой задаче нужно сделать пояснительный рисунок.

а) Направим ось x перпендикулярно стенке. При ударе
скорость молекулы поменяет свое направление на противоположное. Используя закон
изменения импульса тела, получаем, что на молекулу действует импульс силы

Ft = -mv-mv₀=
-2 mv₀ Знак «минус» показывает, что сила, с
которой стенка действует на молекулу, противоположна направлению скорости
v₀. По третьему закону Ньютона молекула
действует на стенку с такой же по модулю, но противоположно направленной силой.
Модуль импульса которой равен 5,6·10^-23Н·с.

(*б) Запишем закон изменения импульса в проекциях на ось х:

F_хt = -m(v_х-v_0х)=m(vcosα+v₀cosα)=2mv₀cosα.

Стенка получает такой же по модулю импульс силы

Ft=2·4,65·10^-25кг·600м/с·0,5=2,8·10^-23Н·с.

IV. Подведение итогов

V. Домашнее задание

§ 21 читать, выучить теорию по тетради, упр.20 письменно, №271.

Источник

Как определить среднюю силу

Как определить среднюю силу

Импульс

Второй закон Ньютона в импульсной форме

Пример вычисления силы

Импульс системы тел

Закон сохранения импульса

Закон сохранения проекции импульса

Определить среднюю силу удара

Порядок выполнения работы

Не пропустите также: