Средняя скорость
- Главная
- /
- Физика
- /
- Средняя скорость
Чтобы найти среднюю скорость воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Средняя скорость на протяжении всего пути
Расстояние (путь)
S =
Время
t =
Средняя скорость
Vср =
0
/
Округление ответа:
Средняя скорость через несколько скоростей
Средняя скорость
Vср =
0
Округление ответа:
Просто введите значения скоростей на разных участках пути и получите среднюю скорость. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой «+».
Теория
Как найти среднюю скорость зная расстояние (путь) и время
Чему равна средняя скорость Vср если известны путь S и время t за которое этот путь преодолён?
Формула
Vср = S⁄t
Пример
К примеру, поезд преодолел расстояние в 1000 км за 16 часов. Посчитаем с какой средней скоростью он двигался:
Vср = 1000/16 = 62.5 км/ч
Как найти среднюю скорость зная скорости на участках пути
Чтобы найти среднюю скорость Vср на протяжении всего пути, зная показатели скорости на его участках (V1 , V2 , … Vn), следует найти среднее гармоническое этих скоростей.
Формула
| Vср | = | n |
| 1⁄V1 + 1⁄V2 + … + 1⁄Vn |
Пример
Средняя скорость через две скорости
Автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути — со скоростью 20 км/ч. Определим среднюю скорость этого автомобиля:
| Vср | = | 2 | = | 2 | = 32 |
| 1⁄80 + 1⁄20 | 0.0125 + 0.05 |
Средняя скорость автомобиля равна 32 км/ч.
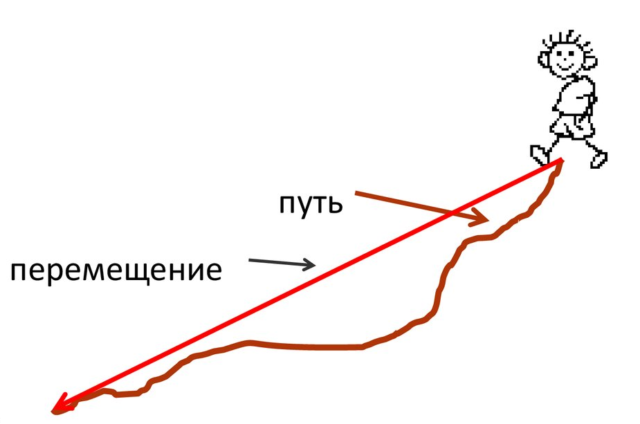
Физическое понятие «скорость» является неоднозначным термином: зависимость от расстояния и времени позволяет ввести два понятия скорости, так как в физике используются векторные (перемещение) и скалярные (модуль перемещения, пройденный путь, время) величины.
1. Отношение вектора перемещения (vec{S}) к интервалу времени (Delta{t}) определяет среднюю (по времени) скорость:
(vec{v}_{ср}=frac{vec{S}}{Delta{t}}) ((1)).
-
Направление вектора средней (по времени) скорости определяется согласно математической формуле ((1)) определения данной физической величины (сравни математическое выражение (vec{a}) (=) (frac{vec{b}}{2}) и формулу ((1))):
Длина вектора (vec{v}_{ср}) не связана с длиной вектора (vec{S}), так как данные физические величины имеют разные размерности (единицы измерения).
-
Числовое значение данной физической величины в случае равномерного прямолинейного движения является постоянным (рис. (1)):
υx=const
.
Примечание: «const» — «постоянный» (сокращение от латинского).
Рис. (1). Изменение координаты точки при равномерном движении
2. При движении тела с постоянной скоростью и его возврате в исходное положение с той же скоростью значение средней (по времени) скорости будет равно нулю.
Отношение пути (l) (длины траектории) к интервалу времени (Delta{t}) определяет средний модуль скорости (среднюю путевую скорость):
(overline{v}=frac{l}{Delta{t}}) ((2)).
Обозначение: черта над символом ((overline{v})) обозначает среднее значение этой величины.
Именно физическое понятие «средняя путевая скорость» используется при описании движения в ситуациях следующего типа: «спортсмен/турист… пробежал/прошёл… дистанцию/расстояние… со средней скоростью <…> м/с».
Источники:
Рис. 1. Изменение координаты точки при равномерном движении. © ЯКласс.
Средняя путевая скорость

4.6
Средняя оценка: 4.6
Всего получено оценок: 166.
Обновлено 30 Июля, 2021
4.6
Средняя оценка: 4.6
Всего получено оценок: 166.
Обновлено 30 Июля, 2021
Из курса физики в 10 классе известно, что быстрота движения характеризуется такой величиной, как скорость. При этом скорость может быть мгновенной, а может быть средней. Средняя скорость, в свою очередь, может рассчитываться по перемещению, а может по пройденному пути. Рассмотрим понятие средней скорости, получим формулу средней путевой скорости.
Мгновенная и средняя скорость
Скорость движения материальной точки — это физическая величина, характеризующая быстроту движения и равная отношению пройденной длины ко времени, за которое эта длина была пройдена:
$$v={Δl over Δt}$$
Поскольку длина в системе СИ измеряется в метрах, а время — в секундах, то скорость измеряется в метрах в секунду.
Наиболее точной является мгновенная скорость, то есть такая скорость, при которой величина $Δt$ стремится к нулю. При этом получающееся значение скорости $v$ может быть постоянным, а может меняться в каждой точке пройденного пути.
Вычисление мгновенной скорости позволяет моделировать движение материальной точки наиболее детально. Однако в реальных условиях настолько большая точность чаще всего не требуется. Как правило, важно, чтобы движение было совершено к определённому моменту времени, а как именно это произошло — не имеет значения.
В этом случае используется понятие средней скорости. Средняя скорость отличается от мгновенной тем, что для вычисления используется сразу весь отрезок времени. Величина $Δt$ в приведённой формуле равна общему времени движения:
$$v_{ср}={l_{общ} over t_{общ}}$$
Средняя путевая скорость
В приведённой формуле числитель (величина $l_{общ}$) может быть рассчитан по-разному.
Во-первых, эта величина может быть равна разности координат в начале и в конце пути. В этом случае мы получаем вектор перемещения $overrightarrow {Δx}$, полученное значение средней скорости также будет вектором $overrightarrow {v_{ср}}$, направленным в ту же сторону.
Во-вторых, эта величина может быть равна длине траектории движения. В этом случае мы получаем пройденный путь $S$. Это скалярная величина, и значение средней скорости $v_{ср}$ также получается скаляром.
Как правило, в физике, когда говорят о средней скорости, имеют в виду первый случай — среднюю скорость по перемещению. В бытовом же обиходе чаще используется длина пройденного пути, и говорят о средней путевой скорости.
Использование средней путевой скорости удобно потому, что затраты на движение (и материальные, и временные), как правило, зависят именно от длины пройденного пути, а не от перемещения. Расстояние между начальным и конечным пунктом по прямой (это и есть перемещение) может быть значительно меньше пути между этими пунктами. Но если нам задана средняя скорость движения транспортного средства, то для нахождения времени прибытия мы должны исходить именно из путевой средней скорости, поскольку при движении будет пройдена вся траектория пути.
Отсюда можно сделать важный вывод — средняя путевая скорость, как правило, больше средней скорости по перемещению (при одинаковом времени). Эти две скорости могут быть равны, только если траектория пути представляет собой прямую.
Ещё одно важное отличие — скалярный характер средней путевой скорости. Зная координаты начального пункта, время пути и вектор средней скорости по перемещению, мы можем найти координаты конечного пункта. Если же известна средняя путевая скорость, то мы можем указать лишь круг (или сферу в трёхмерном пространстве), в пределах которого находится конечный пункт: точные его координаты по средней путевой скорости установить невозможно.
Что мы узнали?
Средняя путевая скорость — это величина, равная отношению пути, пройденного материальной точкой, ко время его прохождения. В формуле средней путевой скорости в качестве расстояния используется длина траектории. Средняя путевая скорость удобна для определения затрат, материальных и временных, на движение.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 166.
А какая ваша оценка?
-
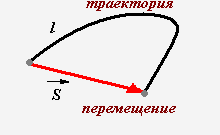
Радиус-вектор, путь перемещения материальной точки
Радиус-вектор
точки
Μ
— направленный отрезок прямой, соединяющий
начало отсчета О
с точкой Μ
(рис.
2).
Путь
s
— скалярная физическая величина,
определяемая длиной траектории, описанной
телом за некоторый промежуток времени.
Путь всегда положителен: s
> 0.
Перемещение
тела
за определенный промежуток времени —
направленный отрезок прямой, соединяющий
начальное (точка M0)
и конечное (точка М)
положение тела (см. рис. 2):
где
и
—
радиусы-векторы тела в эти моменты
времени.
Проекция
перемещения на ось Ox:
,
где x0
и x
— координаты тела в начальный и конечный
моменты времени.
Модуль
перемещения не может быть больше пути:
.
Знак
равенства относится к случаю прямолинейного
движения, если направление движения не
изменяется.
Зная
перемещение и начальное положение тела,
можно найти его положение в момент
времени t:
Траектория
— линия, вдоль которой движется тело.
Путь
— длина траектории.
Перемещение
— вектор, соединяющий начальное и конечное
положения тела.
Положение
тела в пространстве задается радиус
— вектором
или тремя его проекциями
на оси
координат.
Следовательно
закон движения — это зависимость
радиус-вектора от времени или зависимость
координат во времени.
где
-радиус-вектор,
x,
y,
z
—
координаты тела.
6. Средняя путевая и средняя скорость перемещения. Мгновенная линейная скорость.
Средняя
(путевая) скорость —
это отношение длины пути,
пройденного телом, ко времени,
за которое этот путь был пройден:
Средняя
путевая скорость, в отличие от мгновенной
скорости
не является векторной величиной.
Средняя
скорость равна среднему
арифметическому
от скоростей тела во время движения
только в том случае, когда тело двигалось
с этими скоростями одинаковые промежутки
времени.
В
то же время если, например, половину
пути автомобиль двигался со скоростью
180 км/ч, а вторую половину со скоростью
20 км/ч, то средняя скорость будет 36 км/ч.
В примерах, подобных этому, средняя
скорость равна среднему
гармоническому
всех скоростей на отдельных, равных
между собой, участках пути.
Средняя
скорость по перемещению
Можно
также ввести среднюю
скорость по перемещению,
которая будет вектором,
равным отношению перемещения
ко времени, за которое оно совершено:
Средняя
скорость, определённая таким образом,
может равняться нулю даже в том случае,
если точка (тело) реально двигалась (но
в конце промежутка времени вернулась
в исходное положение).
Если
перемещение происходило по прямой
(причём в одном направлении), то средняя
путевая скорость равна модулю средней
скорости по перемещению.
Мгновенная
скорость
— предел средней скорости за бесконечно
малый промежуток времени. Мгновенная
скорость направлена по касательной к
траектории движения в данной точке
траектории.
Средняя
скорость
перемещения
равна отношению полного перемещения к
промежутку времени, за которое это
перемещение совершено.
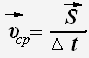
где
ср
-средняя
скорость перемещения,
—
перемещение, ∆
t
— интервал
времени.
Средняя
путевая скорость
равна отношению полного пути к промежутку
времени, за который этот путь пройден.

где
υср
— средняя путевая скорость ,
l
—
путь.
Мгновенная
скорость
— скорость в заданный момент времени.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #