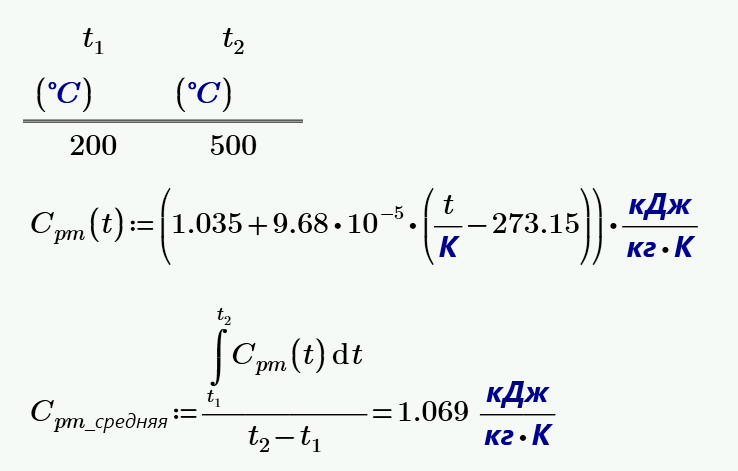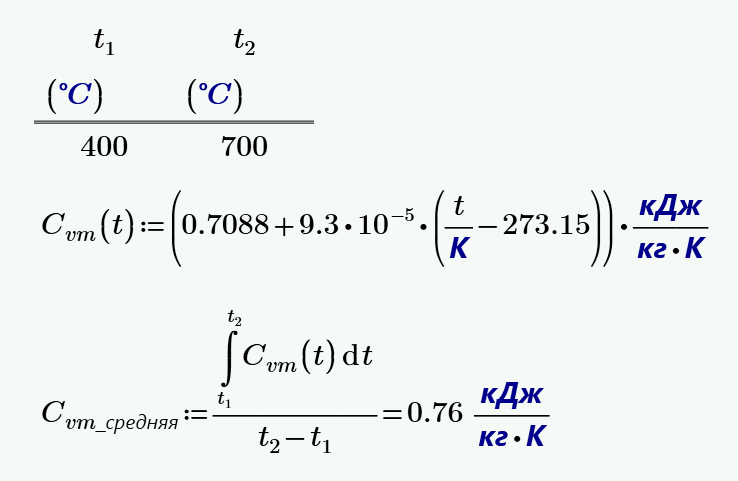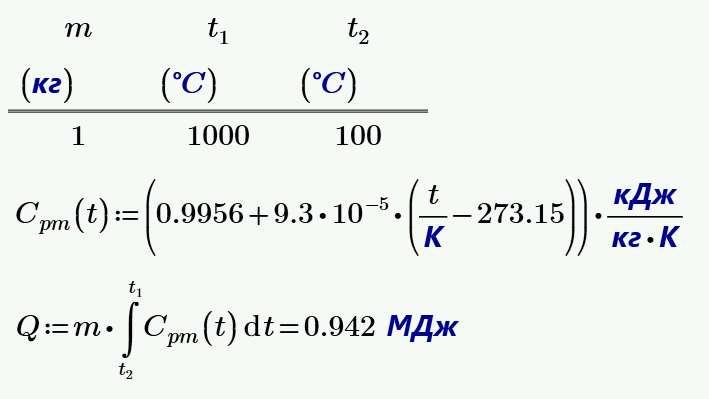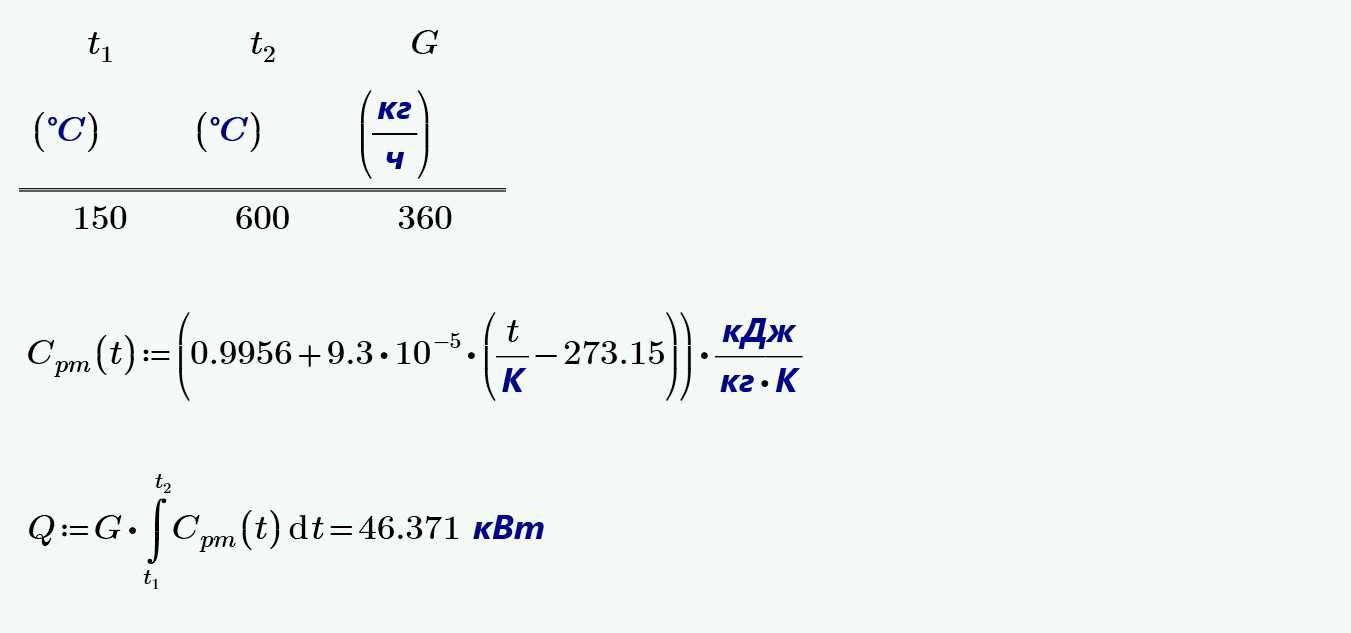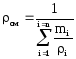Как найти среднюю массовую теплоемкость

Примеры решения задач по теме «Теплоемкость газов»

1. Вычислить среднюю массовую теплоемкость при постоянном давлении $С_{рm}$ для СО в интервале температур от $t_1 = 200$ °С до $t_2 = 500$ °С.

2. Найти среднюю массовую теплоемкость при постоянном объеме $С_{vm}$ для воздуха в интервале температур от $t_1 = 400$ °C до $t_2 = 700$ °C.

3. Воздух в количестве $5$ м³ при абсолютном давлении $Р_1 = 0.3$ МПа и температуре $t_1 = 25$ °С нагревается при постоянном давлении до $t_2 = 100$ °С. Определить количество теплоты, подведенной к воздуху.

4. В закрытом сосуде объемом $V = 300$ л находится воздух при абсолютном давлении $Р_1 = 3$ кгс/см² и температуре $t_1 = 20$ °С. Какое количество теплоты необходимо подвести для того, чтобы температура воздуха поднялась до $t_2 = 120$ °С?

5. Воздух охлаждается от $t_1 = 1000$ °C до $t_2 = 100$ °C в процессе с постоянным давлением. Какое количество теплоты теряет $1$ кг воздуха?

6. Газовая смесь имеет следующий состав по объему: CO = 12 %, O2 = 8 %, H2O = 10 %, N2 = 70 %. Определить для данной смеси среднюю массовую теплоемкость $С_{pm}$ в интервале от $t_1$ до $t_2$ , если смесь нагревается от $t_1 = 100$ °C до $t_2 = 300$ °С.

7. Продукты сгорания топлива поступают в газоход парового котла при температуре газов $t’_г = 1100$ °C и покидают газоход при температуре газов $t»_г = 700$ °C. Объемный состав газов следующий: CO = 11 %, O2 = 6 %, H2O = 10 %, N2 = 73 %. Определить, какое количество теплоты теряет $1$ м³ газовой смеси, взятой при нормальных условиях.

8. В регенеративном подогревателе газовой турбины воздух нагревается от $t_1=150$ °C до $t_2=600$ °C. Определить количество теплоты, сообщенное воздуху в единицу времени, если расход его составляет $360$ кг/ч.

9. Для использования теплоты газов, уходящих из топок паровых котлов, в газоходах последних устанавливают воздухоподогреватели. Пусть известно, что воздух нагревается в воздухоподогревателе от $t’_в=20$ °C до $t»_в= 250$ °C, а продукты сгорания (газы) при этом охлаждаются от $t’_г = 350$ °C до $t»_г = 160$ °С. Объемный состав продуктов сгорания, проходящих через воздухоподогреватель, следующий: CO = 12 %, O2 = 6 %, H2O = 10 %, N2 = 72 %. Принять, что вся теплота, отдаваемая газами, воспринимается воздухом и процесс происходит при неизменном давлении. Определить расход воздуха, приведенный к нормальным условиям $V_{вн}$, если известно, что расход газов $V_{гн} = 66·10^3$ м³н/ч.

10. Найти количество теплоты, необходимое для нагрева $5$ м³ (при нормальных условиях) газовой смеси состава: $CO_2=14.5$ %, $O_2=6.5$ %, $N_2=79$ % от $t_1=200$ °C до $t_2=1200$ °C при $p=const$.

Пример 5.1

При постоянном давлении найти среднюю удельную массовую теплоёмкость кислорода при повышении его температуры от 600 до 2000 ^оС.

Решение

Искомую теплоёмкость принимаем равной истинной удельной изобарной теплоёмкости при средней арифметической температуре ():

 = (600 + 2000) / 2 = 1300 ^оС

Находим в приложении 2 истинную удельную изобарную теплоёмкость кислорода при температуре 1300 ^оС:   = 1,1476 кДж/(кг·К). Это значение теплоёмкости равно средней удельной изобарной теплоёмкости  кислорода в интервале температур 600…2000 ^оС.

Пример 5.2

Найти среднюю молярную изобарную теплоёмкость углекислого газа  при повышении его температуры от 200 до 1000 ^оС.

Решение.

Найти эту теплоёмкость можно найти из первого соотношения (5.1), из которого получаем:

.

Предварительно находим молярную массу (М). Относительная молярная масса углекислого газа М_г = 44,01. Следовательно, его молярная масса РАВНА:

М = 44,01·10^-3 кг/моль.

Среднюю удельную изобарную теплоёмкость () находим из приложения 2 как истинную удельную изобарную теплоёмкость при средней температуре . В нашем примере эта температура равна:

 = (200 + 1000) / 2 = 600 ^оС.

Из приложения 2 находим, что при этой температуре искомая истинная удельная теплоёмкость = 1,1962 кДж/(кг·К). Значит, средняя удельная изобарная теплоёмкость в данном интервале температур тоже равна:

 = 1,1962 кДж/(кг·К).

Теперь можно найти искомую среднюю молярную изобарную теплоёмкость:

 = 1,1962 · 44,01·10^-3 = 52,89 кДж/(моль·К).

Пример 5.3

Воздух, содержащийся в баллоне вместимостью 12,5 м³ при температуре 20 ^оС и абсолютном давлении 1МПа, подогревается до температуры 180 ^оС. Найти подведённую теплоту Q.

Решение

Из определения удельной теплоемкости с учетом того, что процесс нагревания происходит при постоянном объеме, можно записать:

,

откуда

.

Принимая во внимание, что при температуре  = 20 ^оС давление воздуха составляет  = 1 МПа, массу воздуха () найдём из уравнения состояния:

 = 1·10⁶ · 12,5 / (287,1 · 293) = 148,6 кг,

где  = 287,1 Дж/(кг·К) – удельная газовая постоянная воздуха (см. приложение 1).

Среднюю удельную изохорную теплоёмкость принимаем равной истинной теплоёмкости при средней температуре воздуха 100 ^оС, т.е.

 = 722,6Дж/(кг·К).

Следовательно, искомое количество подведенной теплоты равно:

 = 722,6 · 148,6·(180 – 20) = 17,2 МДж.

Пример 5.4

Температура смеси, состоящей из азота массой 3 кг и кислорода массой 2 кг, в результате подвода к ней теплоты при постоянном объёме повышается от 100 до 1100 ^оС. Найти количество подведённой теплоты.

Решение

Искомое количество теплоты (Q) найдем из выражения:

.

Среднюю удельную изохорную теплоёмкость смеси найдём согласно уравнению:

,

где  и  – массовые доли компонентов азота и кислорода.

По условию задачи масса смеси = 3 + 2 = 5 кг.

Следовательно, массовая доля равна:

азота                              = 3 / 5 = 0,6;

кислорода                    = 2 / 5 = 0,4.

Для нахождения теплоёмкостей компонентов смеси  и  воспользуемся приложением 2. Примем, что они равны истинной удельной изохорной теплоёмкости при средней арифметической температуре:

 = (100 + 1100) / 2 = 600 ^оС.

При этой температуре:

для азота                       = 843 Дж/(кг·К);

для кислорода             = 809 Дж/(кг·К).

Найдем теплоёмкость смеси:

 = 0,6 · 843 + 0,4 · 0,809 = 829 Дж/(кг·К)

Подведённая к смеси теплота равна:

 = 5·829·(1100 – 100) = 4,1 МДж.

Пример 5.5

Состав продуктов сгорания бензина в цилиндре двигателя внутреннего сгорания в молях следующий: углекислого газа СО₂ – 71,25, кислорода О₂ – 21,5, азота N₂ – 488,3; паров воды Н₂О – 72,5. Температура газов 800 ^оС. Определить долю тепловых потерь с уходящими газами, если теплота сгорания бензина 43950 кДж/кг.

Решение

Найдём сначала теплоту (Q₁) уходящих газов. Предположим, что сгорание происходит при постоянном давлении, поэтому можно записать:

,

где – средние молярные изобарные теплоёмкости соответственно всей смеси и её компонентов;  – количество вещества соответственно всей смеси и её компонентов.

При среднеарифметической температуре процесса

 = (0 + 800) / 2 = 400 ^оС

средние удельные теплоёмкости компонентов, а также их молярные массы согласно даным, представленных в приложении 2, равны:

для углекислого газа    = 1,11 кДж/(кг·К), М₁ = 44·10^-3 кг/моль;

для кислорода              = 1,02 кДж/(кг·К),  М₂ = 32·10^-3 кг/моль;

для азота                       = 1,09 кДж/(кг·К), М₃ = 28·10^-3 кг/моль;

паров воды                   = 2,08 кДж/(кг·К), М₄ = 18·10^-3 кг/моль.

По найденным значениям удельных теплоёмкостей и молярных масс вычислим значения молярных теплоёмкостей компонентов смеси:

углекислого газа

 = 1,11·44·10^-3 = 48,84 Дж/(моль·К);

кислорода

= 1,02·32·10^-3 = 32,64 Дж/(моль·К);

азота

= 1,09·28·10^-3 = 30,52 Дж/(моль·К);

паров воды

 = 2,06·18·10^-3 = 37,08 Дж/(моль·К).

Найдем количество теплоты, уносимой смесью (выхлопными газами):

;

 = 800·(71,25 · 48,84 + 21,5 · 32,64 + 488,3 · 30,52 + 72,5 · 37,08) = 17,418 кДж.

Обозначив теплоту сгорания бензина через Q, получим, что потеря теплоты с выхлопными газами в процентах составляет:

.

В
инженерной практике часто приходится
иметь дело не с однородными газами, а
со смесями химически не связанных между
собой газов. Примерами газовых смесей
могут служить: атмосферный воздух,
природный газ, газообразные продукты
сгорания топлив и т.д.

Для
газовых смесей справедливы следующие
положения.

1.
Каждый газ, входящий в смесь, имеет
температуру, равную температуре смеси.

2.
Любой из газов, входящих в смесь,
распространяется по всему объему смеси
и поэтому объем каждого газа равен
объему всей смеси.

3.
Каждый из газов, входящих в смесь,
подчиняется своему уравнению состояния.

4.
Смесь в целом является как бы новым
газом и подчиняется своему уравнению
состояния.

В
основе изучения газовых смесей лежит
закон Дальтона, согласно которому при
постоянной температуре давление смеси
равно сумме парциальных давлений газов,
входящих в смесь:

(1.8)

где
p_см
— давление смеси;

p_i

— парциальное давление i-го газа, входящего
в смесь;

n
— число газов, входящих в смесь.

Парциальным
называют давление, которое окажет газ,
входящий в смесь, если он один будет
занимать весь объем смеси при той же
температуре.

Способы
задания газовых смесей

Состав
газовой смеси может быть задан массовыми,
объемными и мольными долями.

Массовые
доли.
Массовой долей любого газа, входящего
в смесь, называется отношение массы
этого газа к массе смеси.

m₁
= M₁
/
M_см;
m₂
= M₂
/
M_см;
……….; m_n
= M_n
/
M_см,

где
m₁,
m₂,
…, m_n
— массовые доли газов;

М₁,
М₂,
…, М_n
— массы отдельных газов;

М_см
— масса смеси.

Нетрудно
видеть, что
и(100%).

Объемные
доли.
Объемной долей любого газа, входящего
в смесь, называется отношение приведенного
(парциального) объема этого газа к объему
смеси.

r₁
= V₁
/
V_см;
r₂
= V₂
/
V_см;
………, r_n
= V_n
/
V_см;

где
V₁,
V₂,
…, V_n
— приведенные объемы газов;

V_см
—
объем смеси;

r₁,
r₂,
…, r_n
— объемные доли газов.

Приведенный
объем — это объем газа при условиях смеси
(при температуре и давлении смеси).

Приведенный
объем можно представить следующим
образом: если из сосуда, где находится
смесь, удалить все газы, кроме одного,
и оставшийся газ сжать до давления
смеси, сохранив температуру, то его
объем и будет приведенным или парциальным.

Можно
доказать, что объем смеси будет равен
сумме приведенных объемов газов.

Тогда

(100%).

Мольные
доли. Мольной
долей любого газа, входящего в смесь,
называется отношение числа киломолей
этого газа к числу киломолей смеси.

r₁
= n₁
/
n_см;
r₂
= n₂
/
n_см;
………, r_n
= n_n
/
n_см,

где
r₁,
r₂,
…, r_n
— мольные доли газов;

n_см
—
число киломолей смеси;

n₁,
n₂,
…, n_n
— число киломолей газов.

Задание
смеси мольными долями тождественно
заданию смеси объемными долями, т.е.
мольные и объемные доли имеют для каждого
газа, входящего в смесь, одинаковые
численные значения.

Газовая
постоянная и кажущаяся (средняя)
молекулярная масса смеси.
Для вычисления газовой постоянной
смеси, заданной массовыми долями, запишем
уравнения состояния:

для
смеси

p_см
×
V_см
= М_смR_смТ;

(1.9)

для
газов

.

(1.10)

Суммируем
левые и правые части уравнений (1.10)

(p₁
+ p₂
+ …. + p_n)
V_см
= (M₁R₁
+ M₂R₂
+
….. + M_nR_n)
T.

Так
как
,

то
p_смV_см
= (M₁R₁
+ M₂R₂
+
….. + M_nR_n)
T.

(1.11)

Из
уравнений (1.9) и ( 1.11) следует, что

М_смR_смТ
= (M₁R₁
+ M₂R₂
+
….. + M_nR_n)
T.

Отсюда

R_см
=
М₁
/ М_см
R₁
+ М₂
/ М_см
R₂
+ …… + М_n
/ М_см
R_n
=

=
m₁R₁
+ m₂R₂
+ …… + m_nR_n

или

,

(1.12)

где
R_см
— газовая постоянная смеси.

Так
как газовая постоянная i-го газа

R_i
= 8314 / m_i,

то
уравнение (1.12) перепишется следующим
образом:

.

(1.13)

Определяя
параметры газовой смеси, удобно
пользоваться некоторой условной
величиной, называемой кажущейся (средней)
молекулярной массой газовой смеси.
Понятие кажущейся молекулярной массы
смеси позволяет условно рассматривать
смесь как однородный газ, что существенно
упрощает расчеты.

Для
отдельного газа справедливо выражение

m_i
R_i
= 8314.

По
аналогии для смеси можно записать

m_см
R_см
= 8314,
(1.14)

где
m_см

— кажущаяся молекулярная масса смеси.

Из
уравнения (1.14), используя выражения
(1.12) и (1.13), получим

,

(1.15)

.

(1.16)

Рассуждая
подобным образом, можно получить формулы
для расчета R_см
и m_см
через объемные доли , формулы для
пересчета массовых долей в объемные
доли и, наоборот, объемных долей в
массовые, формулы для расчета удельного
объема смеси u_см
и плотности смеси r_см
через массовые и объемные доли и, наконец,
формулы для расчета парциальных давлений
газов, входящих в смесь, через объемные
и массовые доли. Приведем эти формулы
без вывода в таблице.

Формулы
для расчета газовых смесей

Теплоемкость
газов

Теплоемкостью
тела называют количество теплоты,
необходимое для нагревания или охлаждения
тела на 1 К. Теплоемкость единицы
количества вещества называют удельной
теплоемкостью.

Итак,
удельной теплоемкостью вещества называют
количество теплоты, которое необходимо
сообщить или отнять от единицы вещества,
чтобы изменить его температуру на 1 К в
данном процессе.

Поскольку
в дальнейшем будут рассматриваться
только удельные теплоемкости, то будем
называть удельную теплоемкость просто
теплоемкостью.

Количество
газа может быть задано массой, объемом
и числом киломолей. Следует оговориться,
что при задании газа объемом этот объем
приводят к нормальным условиям и измеряют
нормальными метрами кубическими (нм³).

В
зависимости от способа задания количества
газа различают следующие теплоемкости:

с
— массовую теплоемкость, Дж/ (кг×К);

с¢
— объемную теплоемкость, Дж/ (нм³
×К);

с_m

— мольную теплоемкость, Дж/(кмоль ×К).

Между
названными теплоемкостями существуют
следующие зависимости:

с
= с_m
/
m;
с_m
= с ×
m;

с¢
= с_m
/
22,4; с_m

= с¢
×
22,4,

отсюда

;
с¢
= с ×
r_н,

где
u_н
и r_н
— удельный объем и плотность при нормальных
условиях.

Изохорная
и изобарная теплоемкости

Количество
теплоты, сообщаемое рабочему телу
зависит от особенностей термодинамического
процесса. Практическое значение имеют
два вида теплоемкости в зависимости от
термодинамического процесса: изохорная
и изобарная.

Теплоемкость
при u
= const — изохорная.

c_u

— массовая изохорная теплоемкость,

c¢_u
— объемная изохорная теплоемкость,

c_mu
— мольная изохорная теплоемкость.

Теплоемкость
при p = const — изобарная.

c_р

— массовая изобарная теплоемкость,

c¢_р
— объемная изобарная теплоемкость,

c_mр
— мольная изобарная теплоемкость.

При
одинаковом изменении температуры в
процессе, осуществляемом при
p
= const, расходуется теплоты больше, чем в
процессе при u
= const. Это объясняется тем, что при u
= const теплота, сообщаемая телу, расходуется
лишь на

изменение
его внутренней энергии, тогда как при
p = const теплота расходуется и на увеличение
внутренней энергии, и на совершение
работы расширения. Разность между
массовой изобарной и массовой изохорной
теплоемкостями по уравнению Майера

c_р
— c_u
=R.

(1.17)

Если
левую и правую части уравнения (1.17)
умножить на массу киломоля m,
то получим

c_mр
— c_mu
=
8314 Дж/(кмоль×К)

(1.18)

В
термодинамике и ее приложениях большое
значение имеет отношение изобарных и
изохорных теплоемкостей:

,

(1.19)

где
к — показатель адиабаты.

Расчеты
показывают, что приближенно можно
принять для одноатомных газов к »
1,67, двухатомных к »
1,4, трехатомных к »
1,29.

Нетрудно
видеть, что значение к
зависит от температуры. Действительно,
из уравнений (1.17) и (1.19) следует, что

,

(1.20)

а
из уравнений (1.18) и (1.19)

.

(1.21)

Так
как с увеличением температуры газа
теплоемкости увеличиваются, то значение
к уменьшается, приближаясь к единице,
но всегда остается больше нее.

Зная
величину к, можно определить значение
соответствующей теплоемкости. Так,
например, из уравнения (1.20) имеем

,

(1.22)

а
т.к. с_р
= к ×
с_u,
то получим

.

(1.23)

Аналогично
для мольных теплоемкостей из уравнения
(1.21) получим

.

(1.24)

.

(1.25)

Средняя
и истинная теплоемкость

Теплоемкость
газов зависит от температуры и в некоторой
степени от давления. Зависимость
теплоемкости от давления невелика и ею
в большинстве расчетов пренебрегают.
Зависимость же теплоемкости от температуры
значительна и ее необходимо учитывать.
Эта зависимость достаточно точно
выражается уравнением

с
= а + вt
+ еt²,
(1.26)

где
а, в
и е — величины, постоянные для данного
газа.

Часто
в теплотехнических расчетах нелинейную
зависимость (1.26) заменяют линейной:

с
= а + вt.
(1.27)

температуры.
Очевидно, что количество теплоты q,
которое сообщают единице количества
вещества при нагревании его от t₁
до t₂,
можно найти, проинтегрировав (1.29) от t₁
до t₂.

.
(1.30)

Графически
интеграл (1.30) выражается площадью
4-1-2-3. Если в выражение (1.30) подставить
значение истинной теплоемкости по
линейной зависимости (1.27), то получим

(1.31)

где
—
средняя теплоемкость в интервале
температур от t₁
до t₂.

,
(1.32)

Следовательно,
средняя теплоемкость представляет
собой отношение конечного количества
теплоты q к конечному изменению температуры
t₂
— t₁:

.
(1.33)

Если
на основании 4-3 (рис.1.4) построить
прямоугольник 4-1¢-2¢-3,
равновеликий фигуре 4-1-2-3, то высота
этого прямоугольника будет равна средней
теплоемкости, где
находится в интервале температур t₁
— t₂.

Обычно
значения средних теплоемкостей приводятся
в таблицах термодинамических свойств
веществ. Однако для сокращения объема
этих таблиц в них приводятся значения
средних теплоемкостей, определенных в
диапазоне изменения температуры от 0
^оС
до t ^оС.

Если
необходимо вычислить значение средней
теплоемкости в заданном интервале
температур t₁
— t₂,
то это можно сделать следующим образом.

Площадь
0а14 под кривой с = f(t) (рис.1.4) соответствует
количеству теплоты q₁,
необходимому для повышения температуры
газа от 0 ^оС
до t₁
^оС.

Аналогично
площадь 0а23 соответствует q₂
при повышении температуры от 0 ^оС
до t₂
^оС:

Таким
образом, q = q₂
— q₁
(площадь 4123) может быть представлено в
виде

(1.34)

Подставляя
значение q по (1.34) в выражение (1.33), получим
формулу для средней теплоемкости в
любом диапазоне температур:

.
(1.35)

Таким
образом, среднюю теплоемкость можно
вычислить по табличным средним
теплоемкостям по уравнению (1.35). Причем
получим нелинейную зависимость с = f(t).
Можно также найти среднюю теплоемкость
по уравнению (1.32) по линейной зависимости.
Значения а и в
в уравнении (1.32) для различных газов
приводятся в литературе.

Количество
теплоты, подведенной или отведенной от
рабочего тела, можно рассчитать по
какому-либо из уравнений:

(1.36)

(1.37)

,
(1.38)

где
— соответственно средняя массовая,
объемная и мольная теплоемкости; М —
масса газа; n — число киломолей газа; V_н
— объем газа при нормальных условиях.

Объем
газа V_н
может
быть найден следующим образом. Записав
уравнение состояния для заданных
условий: pV = MRT и для нормальных условий:

p_нV_н
= MRT_н,
отнесем второе уравнение к первому:

,

отсюда

.
(1.39)

Теплоемкость
газовых смесей

Теплоемкость
газовой смеси может быть вычислена,
если задан состав смеси и известны
теплоемкости компонентов, входящих в
смесь.

Для
нагревания смеси массой М_см
на 1К необходимо температуру каждого
из компонентов также повысить на 1К. При
этом на нагревание i-го компонента смеси
массой М_i
затрачивается количество теплоты,
равное c_iM_i.
Для всей смеси количество теплоты

,

где
c_i
и c_см
— массовые теплоемкости i-го компонента
и смеси.

Поделив
последнее выражение на М_см,
получим
расчетную формулу для массовой
теплоемкости смеси:

,
(1.40)

где
m_i
— массовая доля i-го компонента.

Рассуждая
аналогично, найдем объемную c¢_см
и мольную c_mсм
теплоемкости смеси:

(1.41)

где
c¢_i
— объемная теплоемкость i-го компонента,
r_i
— объемная доля i-го компонента,

,
(1.42)

где
c_mi
— мольная теплоемкость i-го компонента,

r_i
— мольная (объемная) доля i-го компонента.

17

Вычислить среднюю массовую теплоемкость при постоянном давлении cpm
для CO2 в интервале температур от t1=200℃ до t2=680℃. Необходимые данные для расчетов зависимости даны в приложении.
Дано:
t1=200℃;
t2=680℃;
Найти: cpm-?

В справочных данных найдем интерполяционную формулу для определения средней массовой теплоемкости при постоянном давлении для CO2:
cpm=0,8725+0,00024053∙t,
где t-средняя температура.
t=t1+t22=200+6802=440℃.
Рассчитаем среднюю массовую теплоемкость при постоянном давлении для средней температуры в интервале от t1 до t2 :
cpm=0,8725+0,00024053∙t=0,8725+0,00024053∙440=0,9783332 кДж/кг∙град