Как найти среднюю кинетическую энергию движения молекул - Avtoru.top

Физика, 10 класс

Урок 18. Основное уравнение МКТ

Перечень вопросов, рассматриваемых на уроке:

1) средняя кинетическая энергия молекулы;

2) давление газа;

3) основное уравнение МКТ;

Глоссарий по теме:

Давление идеального газа пропорционально произведению концентрации молекул и средней кинетической энергии поступательного движения молекул.

Средняя кинетическая энергия молекул – усреднённая величина, равная половине произведения массы молекулы на среднюю величину квадрата её скорости.

Концентрация – число молекул в единице объёма.

Масса молекулы (или атома) – чрезвычайно маленькая величина в макроскопических масштабах (граммах и килограммах), вычисляется через отношение массы вещества к количеству содержащихся в ней молекул (или атомов).

Изменение импульса тела – произведение силы на время действия силы. Импульс силы всегда показывает, как изменяется импульс тела за данное время.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 188 – 192.
Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. С. 111.
Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. С. 65 – 67.

Открытые электронные ресурсы по теме урока:

http://kvant.mccme.ru/1991/09/idealnyj_gaz_-_universalnaya_f.htm
http://kvant.mccme.ru/1983/10/davlenie_idealnogo_gaza.htm
http://kvant.mccme.ru/1987/09/davlenie_gaza_v_sosude.htm

Теоретический материал для самостоятельного изучения

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами — массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа.

Давление газа на стенку сосуда обусловлено ударами молекул, давление газа пропорционально концентрации молекул: чем больше молекул в единице объема, тем больше ударов молекул о стенку за единицу времени. Каждая молекула при ударе о стенку передает ей импульс, пропорциональный импульсу молекулы m₀v.

Давление пропорционально второй степени скорости, так как, чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории идеального газа имеет вид:

, где m₀ — масса одной молекулы газа,

n— концентрация молекул,

— среднее значение квадрата скорости молекул.

Коэффициент обусловлен трёхмерностью пространства — во время хаотического движения молекул все три направления равноправны.

Средняя кинетическая энергия поступательного движения

тогда уравнение примет вид:

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Примеры и разбор решения заданий.

1. К каждой позиции первого столбца подберите соответствующую позицию второго:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
1) импульс тела	А)
2) средняя кинетическая энергия молекул	Б)
3) давление газа на стенку сосуда	В)
4) концентрация молекул	Г)

Правильный ответ: вспомнив формулы величин, устанавливаем соответствие:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
1) импульс тела	В)
2) средняя кинетическая энергия молекул	А)
3) давление газа на стенку сосуда	Г)
4) концентрация молекул	Б)

2. Кислород находится при нормальных условиях. Средняя квадратичная скорость молекул кислорода в этом случае равна ___ м/с.

Решение:

Ответ: 460 м/с.

Источник

Средняя
кинетическая энергия поступательного
движения молекулы идеального газа
(воспользуемся формулой 2.10)

Е_{кин.

пост.}=

=
=
kТ

Е_{кин.

пост.}
=
kТ
(2.11)

Поступательное
движение молекул может происходить по
осям «Х», «Y»,
«Z»
— есть три поступательных степени
свободы. На одну степень свободы
приходится средняя кинетическая энергия.

Е_кин.
= kТ
(2.12)

Если
у молекулы i
степеней свободы, средняя кинетическая
энергия молекулы

Е_кин.
=
kТ (2.13)

i
— число степеней свободы, число независимых
координат, определяющих положение тела
в пространстве.

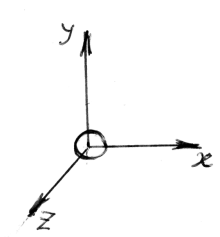
Молекулу
одноатомного идеального газа (например,
инертного газа) можно считать материальной
точкой с тремя степенями свободы (x,
y, z) поступательного движения.

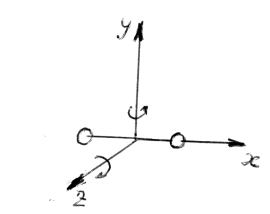
Для
молекулы двухатомного газа можно принять
с некоторыми допущениями модель жесткой
«гантели» с тремя поступательными
степенями свободы (x,
y, z) и двумя вращательными (вокруг оси Y
и оси Z).
Вращение вокруг оси X
(см. рисунок в таблице 2.3) не учитывается,
поскольку поперечные размеры «гантели»
принимаются пренебрежимо малыми. Итого
число степеней свободы молекулы
двухатомного газа i
= 5 (3 поступательных + 2 вращательных).

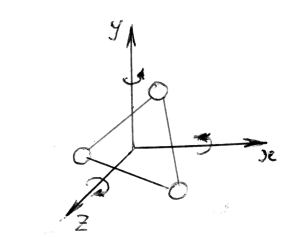
У
молекулы трехатомного и многоатомного
газа, если принять модель жёсткого
трехмерного тела (атомы и молекулы не
расположены на одной прямой), число
степеней свободы i
= 3 поступательных + 3 вращательных = 6

В
этом случае учитывается три вращательных
степени свободы: вокруг оси x,
y и z.

Соответственно
средние кинетические энергии молекул
будут равны:

Для
молекулы одноатомного газа – kТ,

Двухатомного
—
kТ,

Трех-
и многоатомного – 3kТ
(см. таблицу 2.3).

Таблица
2.3. Средние кинетические энергии молекул
идеального газа

Газ	рисунок	Число степеней свободы	Средняя кинетическая энергия молекулы газа, Е_кин.
Одноатомный		3 поступательных	kТ
Двухатомный		3 пост + 2 вращ. = 5	kТ
Трехатомный		3 пост + 3 вращ. = 6	kТ= 3kТ

Внутренняя
энергия идеального тела U
(см 1.2) складывается из суммарной
кинетической энергии движения молекул
относительно друг друга Е_кин_i
, суммарной потенциальной энергии
взаимодействия молекул друг с другом
и энергии U₀
внутримолекулярных, внутриатомных,
внутриядерных движений и взаимодействий
и т. д. и т. д.

Будем
считать, что в изучаемых нами в этой
главе молекулярных явлениях эта часть
внутренней энергии U₀
не меняется.

Итак,
внутренняя энергия идеального газа:

(2.14)

Но
так как в модели идеального газа
пренебрегаем взаимодействиями молекул
на расстоянии

0 и остается

U
= 
Екин
i
+
U₀
(2.15)

а

Е_кин_i
=kT,
где

N
– число молекул,

kT
– средняя кинетическая энергия одной
молекулы (согласно 2.13).

Поэтому

U
= kT
+ U₀

А
так как

N
= N_Аm/М,

U
= N_А
kT
+ U₀

Учтя,
что

N_Аk
= R,
получим для внутренней энергии идеального
газа

U
=
R
T
+ U₀
(2.16)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
12.02.201514.57 Mб29Уход за хирургическими больными. Буянов В.М.pdf
#
#
#
#
#
#
#
#
#

Источник

Уравнение состояния идеального газа в форме (p=frac 13nm_0overline {v^2}) или (p=frac 23noverline E) может быть обосновано и методами кинетической теории газов. На основе кинетического подхода сравнительно просто выводится выражение для давления идеального газа в сосуде, которое получается как результат усреднения импульсов молекул, передаваемых стенке сосуда при многочисленных соударениях молекул со стенкой. Величина получаемого при этом давления определяется как

(p=frac 13nmbig (v^2big)),

где (v^2) – среднее значение квадрата скорости молекул, (m) – масса молекулы.

Средняя кинетическая энергия молекул газа (в расчете на одну молекулу) определяется выражением

(E_k=frac 12mbig (v^2big)).

Кинетическая энергия поступательного движения атомов и молекул, усредненная по огромному числу беспорядочно движущихся частиц, является мерилом того, что называется температурой. Если температура T измеряется в градусах Кельвина (К), то связь ее с (E_k) дается соотношением

(E_k=frac 32 kT).

Это соотношение позволяет, в частности, придать более отчетливый физический смысл постоянной Больцмана (k = 1,38·10^{–23}) Дж/K, которая фактически является переводным коэффициентом, определяющим, какая часть джоуля содержится в градусе.

Используя (6) и (7), находим, что (frac 13m v^2 = kT). Подстановка этого соотношения в формулу для энергии приводит к уравнению состояния идеального газа в форме

(p = nkT,) которое уже было получено из уравнения Клапейрона – Менделеева.

Также из уравнений можно определить значение среднеквадратичной скорости молекул:

((v)_{ке}=sqrt{(v^2)}=big (frac {3kT}{m}big )^{frac 12}=big (frac{3RT}Mbig )^{frac 12}).

Расчеты по этой формуле при (T = 273) K дают для молекулярного водорода (v_{кв} = 1838 ) м/с, для азота – (493 ) м/с, для кислорода – (461) м/с и т. д.

Напомним, что газообразное состояние возникает тогда, когда энергия теплового движения молекул вещества превышает энергию их взаимодействия. Молекулы вещества в этом состоянии приобретают прямолинейное поступательное движение, а индивидуальные свойства веществ теряются, и они подчиняются общим для всех газов законам. Газообразные тела не имеют собственной формы и легко изменяют свой объем при воздействии внешних сил или при изменении температуры.

Плотность идеального газа в сосуде – (1,2) кг/м(^3). Если средняя квадратичная скорость молекул газа равна (500) м/с, то газ находится под давлением
Давление кислорода и водорода при одинаковых концентрациях молекул и равных средних квадратичных скоростях их движения находятся в соотношении (М((O_2)) (= 0,032) кг/моль; М((H_2)) (= 0,002) кг/моль)
В вакуумном диоде электроны ускоряются до энергии (140) эВ. Их минимальная скорость у анода лампы равна

(e (= 1,6 ⋅ 10^{-19}) Кл; (m_e) (= 9 ⋅ 10^{-31}) кг; (1) эВ (= 1,6 ⋅ 10^{-19})Дж)
Объем одноатомного газа уменьшили в (2) раза, а среднюю кинетическую энергию молекул увеличили в (3) раза. Определите изменение давления.
Найдите среднюю кинетическую энергию атома аргона, если температура газа равна (117^{circ}C) ((k = 1,38 ⋅ 10^{-23})(frac{Дж}{К})).
Чему равна энергия покоя электрона? ((c = 3 ⋅ 10^8)м/с; (m = 9,1 ⋅ 10^{-31})кг)
Во сколько раз отличаются средние квадратичные скорости молекул диоксида серы и гелия при одинаковой температуре?

(M(_{SO_2}) (= 64 ⋅ 10^{-3})(frac{кг}{моль}); M(_{He}) (= 4 ⋅ 10^{-3})(frac{кг}{моль}))
Во сколько раз изменится среднеквадратичная скорость движения частиц одноатомного идеального газа (υ), если, не меняя его плотности, увеличить давление в (9) раз?
Среднеквадратичная скорость молекул идеального одноатомного газа, заполняющего закрытый сосуд, равна (0,25) км/с. Газ охладили, уменьшив при этом давление на (19%). Как и на сколько изменилась среднеквадратичная скорость молекул этого газа?
Одноатомный газ находится при давлении в (400) кПа. Чему будет равна средняя кинетическая энергия молекул этого газа, если в (1) м(^3) содержится примерно (2·10^{27}) молекул?
Маленькая частичка массой (19,2cdot10^{-12}) кг находится в воздухе. Во сколько раз ее средняя квадратичная скорость будет отличаться от средней квадратичной скорости движения молекул воздуха? (Молярная масса воздуха – (0,029) кг/моль)
Вычислите среднюю квадратичную скорость молекул газа, находящегося под давлением (10) кПа, если его масса равна (3) кг, объем – (16) м(^3).
Можно ли получить температуру ниже или равную абсолютному нулю?
При нагревании ртуть в градуснике расширилась. Что это означает?
Найдите давление углекислого газа в сосуде, если концентрация его молекул равна (2,7 · 10^{20}) м(^{–3}), а среднее значение квадрата их скорости – (3 · 10^4) м(^2)/с(^2). (Масса молекулы углекислого газа равна (7,3 · 10^{–26}) кг)

Источник

Уравнение состояния идеального газа

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: модель идеального газа, связь между давлением и средней кинетической энергией теплового движения молекул идеального газа, связь температуры газа со средней кинетической энергией его частиц, уравнение , уравнение Менделеева—Клапейрона.

Из трёх агрегатных состояний вещества наиболее простым для изучения является газообразное. В достаточно разреженных газах расстояния между молекулами намного больше размеров самих молекул (тогда как в жидкостях и твёрдых телах молекулы «упакованы» весьма плотно).Поэтому силы взаимодействия между молекулами таких газов очень малы.

Для описания разреженных газов в физике используется модель идеального газа. В рамках этой модели делаются следующие допущения.

1. Пренебрегаем размерами молекул. Иными словами, молекулы газа считаются материальными точками.
2. Пренебрегаем взаимодействием молекул на расстоянии.
3. Соударения молекул друг с другом и со стенками сосуда считаем абсолютно упругими.

Таким образом, идеальный газ — это газ, частицы которого являются не взаимодействующими на расстоянии материальными точками и испытывают абсолютно упругие соударения друг с другом и со стенками сосуда.

Средняя кинетическая энергия частиц газа

Оказывается, что ключевую роль в описании идеального газа играет средняя кинетическая энергия его частиц.

Частицы газа двигаются с разными скоростями. Пусть в газе содержится частиц, скорости которых равны . Масса каждой частицы равна m_0 . Кинетические энергии частиц:

$E_1=frac{displaystyle m_0 v_1^2}{displaystyle 2 vphantom{1^a}}, E_2=frac{displaystyle m_0 v_2^2 }{displaystyle 2 vphantom{1^a}}, ldots,E_N=frac{displaystyle m_0 v_N^2}{displaystyle 2 vphantom{1^a}}.$

Средняя кинетическая энергия частиц газа это среднее арифметическое их кинетических энергий:

$E=frac{displaystyle E_1+E_2+ ldots+E_N}{displaystyle N vphantom{1^a}}= frac{displaystyle 1}{displaystyle N vphantom{1^a}}left ( frac{displaystyle m_0 v_1^2}{displaystyle 2 vphantom{1^a}}+frac{displaystyle m_0 v_2^2}{displaystyle 2 vphantom{1^a}}+ ldots + frac{displaystyle m_0 v_N^2}{displaystyle 2 vphantom{1^a}} right ) =frac{displaystyle m_0}{displaystyle 2 vphantom{1^a}} frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}.$

Последний множитель — это средний квадрат скорости, обозначаемый просто v_2 :

$v_2=frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}.$

Тогда формула для средней кинетической энергии приобретает привычный вид:

$E=frac{displaystyle m_0 v^2}{displaystyle 2 vphantom{1^a}}.$ (1)

Корень из среднего квадрата скорости называется средней квадратической скоростью:

$v=sqrt{ frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}}.$

Основное уравнение МКТ идеального газа

Cвязь между давлением газа и средней кинетической энергией его частиц называется основным уравнением молекулярно-кинетической теории идеального газа. Эта связь выводится из законов механики и имеет вид:

$p= frac{displaystyle 2}{displaystyle 3 vphantom{1^a}} nE.$ (2)

где — концентрация газа (число частиц в единице объёма). С учётом (1) имеем также:

$p= frac{displaystyle 1}{displaystyle 3 vphantom{1^a}} m_0 nv^2.$ (3)

Что такое m_0n ? Произведение массы частицы на число частиц в единице объёма даёт массу единицы объёма, то есть плотность: . Получаем третью разновидность основного уравнения:

$p= frac{displaystyle 1}{displaystyle 3 vphantom{1^a}} rho v^2.$ (4)

Энергия частиц и температура газа

Можно показать, что при установлении теплового равновесия между двумя газами выравниваются средние кинетические энергии их частиц. Но мы знаем, что при этом становятся равны и температуры газов. Следовательно, температура газа — это мера средней кинетической энергии его частиц.

Собственно, ничто не мешает попросту отождествить эти величины и сказать, что температура газа — это средняя кинетическая энергия его молекул. В продвинутых курсах теоретической физики так и поступают. Определённая таким образом температура измеряется в энергетических единицах — джоулях.

Но для практических задач удобнее иметь дело с привычными кельвинами. Связь средней кинетической энергии частиц и абсолютной температуры газа даётся формулой:

$E= frac{displaystyle 3}{displaystyle 2 vphantom{1^a}} kT,$ (5)

где $k=1,38 cdot 10^{-23}$ Дж/К — постоянная Больцмана.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Уравнение состояния идеального газа» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Как найти среднюю кинетическую энергию молекул

Молекула является объектом микромира. Поэтому непосредственное измерение ее кинетической энергии невозможно. Средняя кинетическая энергия является статистическим понятием. Это усредненное значение кинетических энергий всех молекул, входящих в вещество.

Вам понадобится

— периодическая таблица химических элементов;
— термометр;
— калькулятор.

Инструкция

Найдите среднюю кинетическую энергию, используя значение средней скорости молекул вещества. Рассчитайте массу одной молекулы вещества. Для этого определите его молярную массу в килограммах на моль при помощи периодической таблицы химических элементов. Для этого найдите относительные атомные массы всех элементов, входящих в состав молекулы вещества. Они указаны в соответствующих ячейках таблицы. Сложите их, и получите относительную молекулярную массу молекулы. Поделите это число на 1000 и получите молярную массу вещества в килограммах на моль.

Поделите молярную массу на число Авогадро (NA=6,022∙10^23 1/моль) и получите массу одной молекулы вещества m0 в килограммах. Посчитайте среднюю кинетическую энергию молекул, умножив массу одной молекулы m0 на квадрат ее скорости v, а результат поделите на 2 (Ek=m0∙v²/2).

Пример. Рассчитайте среднюю кинетическую скорость молекул азота, если их средняя скорость равна 100 м/с. Молярная масса двухатомной молекулы азота равна 0,028 кг/моль. Найдите массу одной молекулы 0,028/(6,022∙10^23)≈4,6∙10^(-25) кг. Определите среднюю кинетическую энергию молекул Ek= 4,6∙10^(-25)∙100²/2=2,3∙10^(-21) Дж.

Найдите среднюю кинетическую энергию молекул газа через значение температуры. Измерьте эту величину термометром. Если прибор измеряет в градусах Цельсия, переведите значение температуры в Кельвины по абсолютной шкале. Для этого к значению температуры в градусах Цельсия прибавьте число 273. Например, если температура газа 23ºС, то по абсолютной шкале его температура будет равна Т=23+273=296 К.

Определите степень свободы молекулы i. Эта величина для одноатомной молекулы равна 3. Для двухатомной частицы – 5, трехатомной и более – 6. Рассчитайте среднюю кинетическую энергию, умножив степень свободы молекулы на абсолютную температуру газа и постоянную Больцмана (k=1,38∙10^(-23)). Результат поделите на число 2 (Ek=i∙k∙T/2).

Пример. Найдите среднюю кинетическую энергию молекул двухатомного газа при температуре 85ºС. Определите температуру газа по абсолютной шкале Т=85+273=358К. Степень свободы двухатомной молекулы i=5. Произведите расчет Ek=5∙1,38∙10^(-23)∙358/2≈1,24∙10^(-20) Дж.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Уравнение состояния идеального газа

Средняя кинетическая энергия частиц газа

Основное уравнение МКТ идеального газа

Энергия частиц и температура газа

Как найти среднюю кинетическую энергию молекул

Не пропустите также: