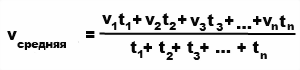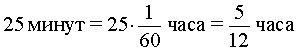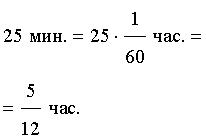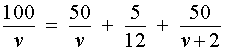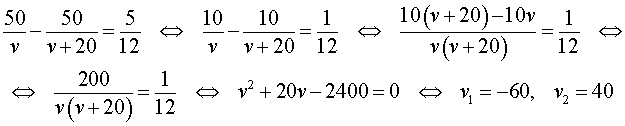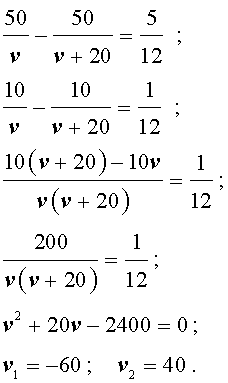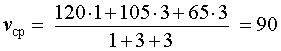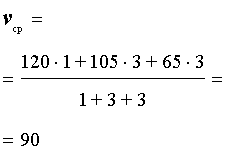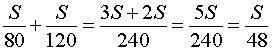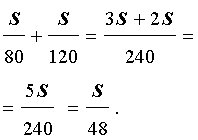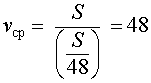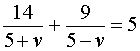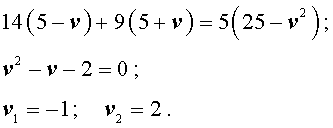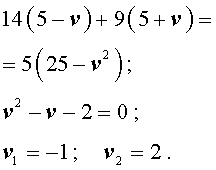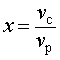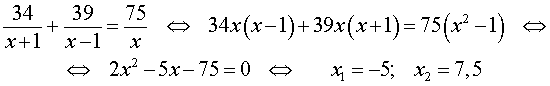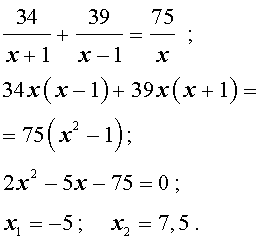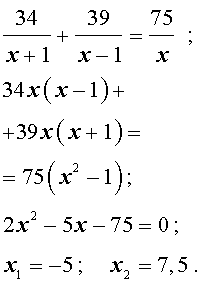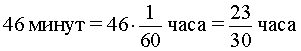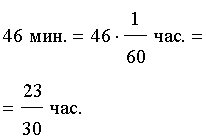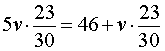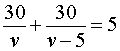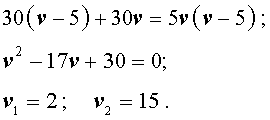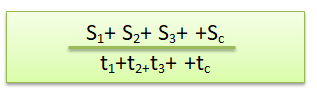Как найти среднюю арифметическую скорость поезда

Перейти к контенту

ГДЗ по математике 5 класс Мерзляк 36. Среднее арифметическое. Среднее значение величины

ГДЗ по Математике 5 класс Мерзляк А.Г. § 36. Среднее арифметическое. Среднее значение величины

1037. 1) Поезд ехал 4 ч со скоростью 64 км/ч и 5 ч со скоростью 53,2 км/ч. Найдите среднюю скорость поезда на протяжении всего пути.

Ответ

Поезд ехал 4 ч со скоростью 64 км/ч и 5 ч со скоростью 53,2 км/ч.

1) 64 • 4 = 256 (км) — проехал поезд в первый отрезок времени.

2) 53,2 • 5 = 266 (км) — проехал поезд во второй отрезок времени.

3) 256 + 266 = 522 (км) — проехал поезд всего.

4) 4 + 5 = 9 (часов) — двигался поезд всего.

5) 522 : 9 = 58 (км/ч) — средняя скорость поезда.

Поезд ехал 4 ч со скоростью 64 км/ч и 5 ч со скоростью 53,2 км/ч.

Ответ: 58 км/ч.

2) В автомастерской работает 10 человек. У двоих из них месячная зарплата составляет 22 800 р., у четверых — 28 000 р., у троих 31 000 р., а у одного 32 000 р. Какова средняя зарплата работников мастерской?

Поезд ехал 4 ч со скоростью 64 км/ч и 5 ч со скоростью 53,2 км/ч.

(22 800 • 2 + 28 000 • 4 + 31 000 • 3 + 32 000) : 10 = 282 600 : 10 = 28 260 (рублей) — средняя месячная зарплата работников.

Поезд ехал 4 ч со скоростью 64 км/ч и 5 ч со скоростью 53,2 км/ч.

Ответ: 28 260 рублей.

Источник

Средняя скорость

  1. Главная
  2. /
  3. Физика
  4. /
  5. Средняя скорость

Чтобы найти среднюю скорость воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Средняя скорость на протяжении всего пути

Расстояние (путь)

S =

Время

t =

Средняя скорость

Vср =

0

/

Округление ответа:

Средняя скорость через несколько скоростей

Средняя скорость

Vср =

0

Округление ответа:

Просто введите значения скоростей на разных участках пути и получите среднюю скорость. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой «+».

Теория

Как найти среднюю скорость зная расстояние (путь) и время

Чему равна средняя скорость Vср если известны путь S и время t за которое этот путь преодолён?

Формула

Vср = S⁄t

Пример

К примеру, поезд преодолел расстояние в 1000 км за 16 часов. Посчитаем с какой средней скоростью он двигался:

Vср = 1000/16 = 62.5 км/ч

Как найти среднюю скорость зная скорости на участках пути

Чтобы найти среднюю скорость Vср на протяжении всего пути, зная показатели скорости на его участках (V1 , V2 , … Vn), следует найти среднее гармоническое этих скоростей.

Формула

Vср = n
1⁄V1 + 1⁄V2 + … + 1⁄Vn

Пример

Средняя скорость через две скорости

Автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути — со скоростью 20 км/ч. Определим среднюю скорость этого автомобиля:

Vср = 2 = 2 = 32
1⁄80 + 1⁄20 0.0125 + 0.05

Средняя скорость автомобиля равна 32 км/ч.

Источник

Повторим, как находить среднюю скорость, и рассмотрим конкретные примеры.

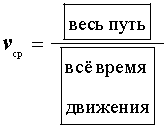
Чтобы найти среднюю скорость, надо:

1) найти весь пройденный путь;

2) найти все время движения;

3) весь пройденный путь разделить на все время движения:

формула средней сорости

На примерах посмотрим, как находить среднюю скорость.

1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч. Найти среднюю скорость движения пешехода на всем пути.

Решение:

Находим весь пройденный путь: 2∙7 + 3∙5 = 29 км.

Находим все время движения: 2+3=5 часов.

Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.

2) Автомобиль проехал 2 часа по шоссе со скоростью 100 км/ч, 1,5 часа по грунтовой дороге со скоростью 40 км/ч и 30 минут по проселочной дороге со скоростью 26 км/ч. Найти среднюю скорость автомобиля на всем пути.

Решение:

Переведем минуты в часы: 30 минут = 0,5 часа.

Найдем весь пройденный автомобилем путь:

2∙100 + 1,5∙40 + 0,5∙26 = 200 + 60 + 13= 273 км.

Находим все время движения:

2 + 1,5 + 0,5 = 4 часа.

Чтобы найти среднюю скорость движения автомобиля, разделим весь пройденный путь на все время движения:

273:4 = 68,25 км/ч.

3) Велосипедист проехал 3 часа со скоростью 12 км/ч, затем отдохнул час, после чего продолжил путь со скоростью 9 км/ч и проехал еще 2 часа. Найти среднюю скорость движения велосипедиста на всем пути.

Решение:

Найдем весь путь велосипедиста:

3∙12 + 1∙0 + 2∙9 = 54 км.

Найдем все время движения:

3 + 1 + 2 = 6 часов.

Чтобы найти среднюю скорость движения велосипедиста, весь путь делим на все время движения:

54:6=9 км/ч.

Источник

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела движение по реке скорость течения реки движение по течению движение против течения движение по кольцу движение по кольцевым трассам примеры решения задач

Скорость тела. Средняя скорость тела

      Решение задач на движение опирается на хорошо известную из курса физики формулу

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

позволяющую найти путь   S ,   пройденный за время   t   телом, движущимся с постоянной скоростью   v .

      Сразу же сделаем важное

      Замечание 1. Единицы измерения величин   S ,   t   и   v   должны быть согласованными. Например, если путь измеряется в километрах, а время – в часах, то скорость должна измеряться в км/час.

      В случае, когда тело движется с разными скоростями на разных участках пути, вводят понятие средней скорости, которая вычисляется по формуле

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

 (1)

      Например, если тело в течение времени   t1   двигалось со скоростью   v1 ,  в течение времени   t2   двигалось со скоростью   v2 ,  в течение времени   t3   двигалось со скоростью   v3 ,  то средняя скорость

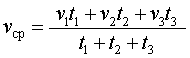задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач (2)

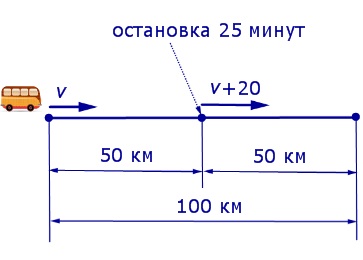
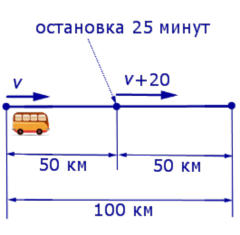
      Задача 1. По расписанию междугородный автобус должен проходить путь в   100   километров с одной и той же скоростью и без остановок. Однако, пройдя половину пути, автобус был вынужден остановиться на   25   минут. Для того, чтобы вовремя прибыть в конечный пункт, водитель автобуса во второй половине маршрута увеличил скорость на   20   км/час. Какова скорость автобуса по расписанию?

      Решение. Обозначим буквой   v   скорость автобуса по расписанию и будем считать, что скорость   v   измеряется в км/час. Изобразим данные, приведенные в условии задачи 1, на рисунке 1.

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

Рис. 1

      Тогда

     задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач – время движения автобуса по расписанию (в часах);

      задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач – время, за которое автобус проехал первую половину пути (в часах);

      v + 20   – скорость автобуса во второй половине пути (в км/час);

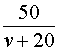
      задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач – время, за которое автобус проехал вторую половину пути (в часах).

      В условии задачи дано время остановки автобуса –   25   минут. Его необходимо выразить в часах, чтобы все единицы измерения были согласованными:

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

      Теперь можно составить уравнение, исходя из того, что автобус прибыл в конечный пункт вовремя, а, значит, время, которое он был в пути, плюс время остановки должно равняться времени движения автобуса по расписанию:

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

      Решим это уравнение:

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

      По смыслу задачи первый корень должен быть отброшен.

      Ответ.   40   км/час.

      Задача 2. (МИОО) Первый час автомобиль ехал со скоростью   120   км/час, следующие три часа – со скоростью   105   км/час, а затем три часа – со скоростью   65   км/час. Найдите среднюю скорость автомобиля на протяжении всего пути.

      Решение. Воспользовавшись формулой (2), получаем

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

      Ответ.   90   км/час.

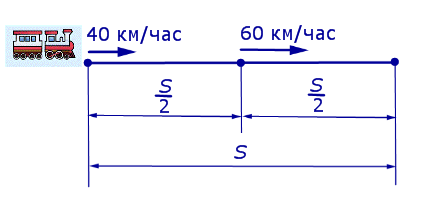
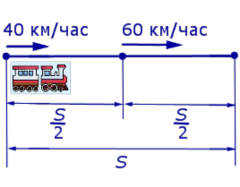
      Задача 3. Первую половину пути поезд шел со скоростью   40   км/час, а вторую половину пути – со скоростью   60   км/час. Найдите среднюю скорость поезда на протяжении всего пути.

      Решение. Обозначим буквой   S   длину всего пути, выраженную в километрах. Изобразим данные, приведенные в условии задачи 3, на рисунке 2.

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

Рис. 2

      Тогда

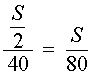
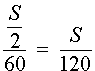
      задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач – время, за которое поезд прошел первую половину пути, выраженное в часах;

      задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач – время, за которое поезд прошел вторую половину пути, выраженное в часах.

      Следовательно, время, за которое поезд прошел весь путь, равно

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

      В соответствии с формулой (1) средняя скорость поезда на протяжении всего пути

задачи на составление уравнений задачи на движение скорость тела средняя скорость тела примеры решения задач

      Ответ.   48   км/час.

      Замечание 2. Средняя скорость поезда в задаче 3 равна   48   км/час, а не   50   км/час, как иногда ошибочно полагают, вычисляя среднее арифметическое чисел (скоростей)   40   км/час и   60   км/час. Средняя скорость не равна среднему арифметическому скоростей, а является величиной, вычисляемой по формуле (1).

Движение по реке. Скорость течения реки

      В отличие от задач на движение по суше, в задачах на движение по реке появляется новая величина – скорость течения реки.

      По отношению к берегу, который неподвижен, скорость тела, движущегося по течению реки, равна сумме собственной скорости тела (скорости тела по озеру, скорости тела в неподвижной воде, скорости тела в стоячей воде) и скорости течения реки. По отношению к берегу скорость тела, движущегося против течения реки, равна разности собственной скорости тела  и скорости течения реки.

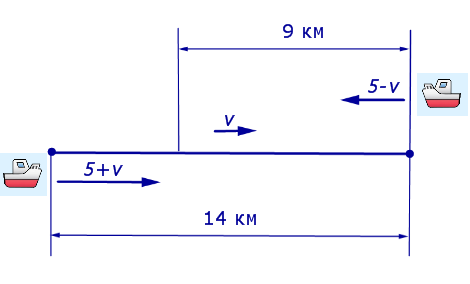
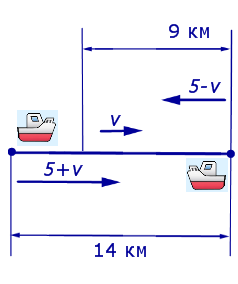
      Задача 4. Моторная лодка прошла по течению реки   14   км, а затем   9   км против течения, затратив на весь путь   5   часов. Скорость лодки в стоячей воде   5   км/час. Найдите скорость течения реки.

      Решение. Обозначим буквой   v   скорость течения реки и будем считать, что скорость   v   измеряется в км/час.Изобразим данные, приведенные в условии задачи 4, на рисунке 3.

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

Рис. 3

      Тогда

      5 + v   – скорость, с которой лодка шла по течению реки (в км/час);

      задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач – время движения лодки по течению реки (в часах);

      5 – v   – скорость, с которой лодка шла против течения реки (в км/час);

      задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач – время движения лодки против течения реки (в часах);

      Теперь можно составить уравнение, принимая во внимание тот факт, что лодка находилась в пути   5   часов:

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

      Решим это уравнение:

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

      По смыслу задачи первый корень должен быть отброшен.

      Ответ.   2   км/час.

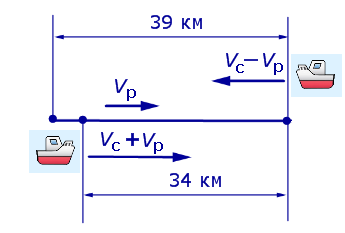
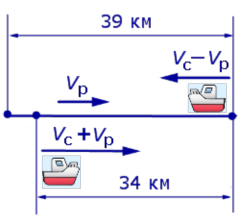
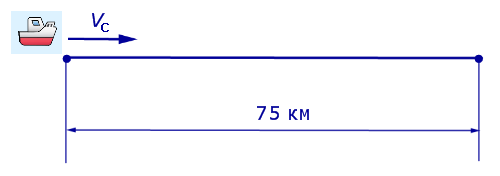
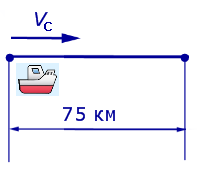
      Задача 5. (Бюро «Квантум») Моторная лодка прошла по течению реки   34   км и   39   км против течения, затратив на это столько же времени, сколько ей нужно, чтобы пройти   75   километров в стоячей воде. Найдите отношение скорости лодки в стоячей воде к скорости течения реки.

      Решение. Обозначим   vс   (км/ч) скорость лодки в стоячей воде и обозначим   vр   (км/ч) скорость течения реки. Изобразим данные задачи 5 на рисунках 4 и 5.

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

Рис. 4

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

Рис. 5

      Учитывая тот факт, что в обеих ситуациях лодка провела в пути одно и то же время, можно составить уравнение:

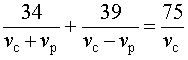задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач (3)

      Если ввести обозначение

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

то, воспользовавшись формулой

vс = xvр ,

перепишем уравнение (3) в виде

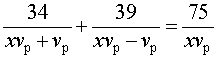задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач (4)

      Умножая уравнение (4) на   vр ,   получим

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

задачи на составление уравнений задачи на движение движение по реке скорость течения реки движение по течению движение против течения примеры решения задач

      По смыслу задачи первый корень должен быть отброшен.

      Ответ.   7,5 .

Движение по кольцевым трассам

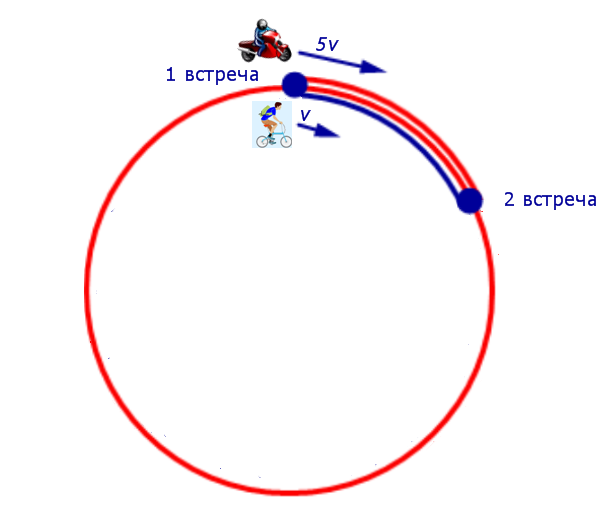
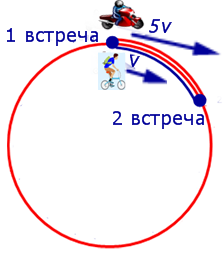
      Задача 6. (www.reshuege.ru) Из пункта   A   круговой трассы длиной   46   км выехал велосипедист, а через   20   минут из пункта   A   следом за велосипедистом отправился мотоциклист. Через   5   минут после отправления мотоциклист догнал велосипедиста в первый раз, а еще через   46   минут после этого мотоциклист догнал велосипедиста во второй раз. Найдите скорости велосипедиста и мотоциклиста.

      Решение. К тому моменту, когда мотоциклист в первый раз догнал велосипедиста, мотоциклист ехал   5   минут, а велосипедист ехал   25   минут, причем проехали они один и тот же путь. Отсюда вытекает, что скорость мотоциклиста в   5   раз больше скорости велосипедиста.

      Таким образом, обозначив буквой   v   (км/час) скорость велосипедиста, получаем, что скорость мотоциклиста равна   5v   (км/час).

      В условии задачи дано время, прошедшее между двумя последовательными встречами мотоциклиста и велосипедиста, –   46   минут. Это время необходимо выразить в часах, чтобы все единицы измерения были согласованными:

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

      Изобразим данные задачи, касающиеся движения мотоциклиста и велосипедиста между первой и второй встречами, на рисунке 6.

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

Рис. 6

      Поскольку за время задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач часа, прошедшее от момента первой встречи до момента второй встречи, мотоциклист проехал   46   км (вся круговая трасса) плюс путь, который проехал велосипедист за задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач часа, то можно составить следующее уравнение:

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

      Решая это уравнение, находим скорость велосипедиста:

v = 15 .

      Ответ. Скорость велосипедиста   15   км/час, скорость мотоциклиста   75   км/час.

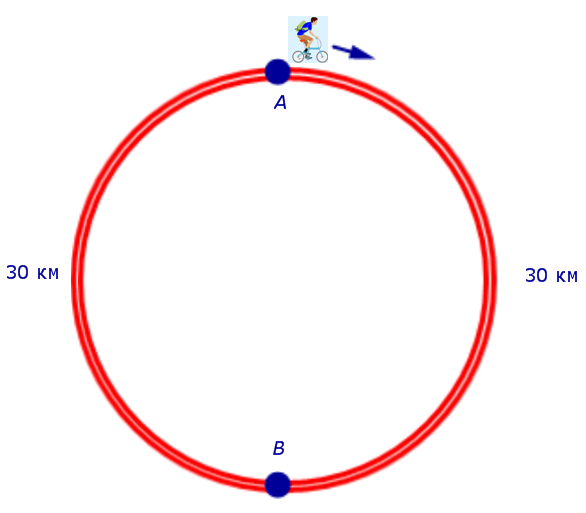
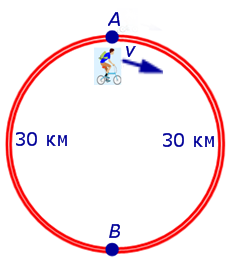
      Задача 7. На дороге, представляющей собой окружность длиной   60   км, пункты   A   и   B   являются диаметрально противоположными точками. Велосипедист выехал из пункта   A   и сделал два круга. Первый круг он прошел с постоянной скоростью, после чего уменьшил скорость на   5   км/час. Время между двумя прохождениями велосипедиста через пункт   B   равно   5   часам. Найти скорость, с которой велосипедист прошел первый круг.

      Решение. Для определенности будем считать, что велосипедист двигался по кругу по часовой стрелке и рассмотрим рисунок 7.

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

Рис. 7

      Если обозначить буквой   v   (км/час) скорость, с которой велосипедист прошел первый круг, то скорость велосипедиста на втором круге будет равна   v – 5   (км/час), и можно составить уравнение

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

      Решая это уравнение, находим скорость велосипедиста на первом круге:

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

задачи на составление уравнений задачи на движение движение по кольцу движение по кольцевым трассам примеры решения задач

      Поскольку скорость велосипедиста на первом круге больше, чем   5   км/час, то первый корень должен быть отброшен.

      Ответ.   15   км/час.

Подготовка к ЕГЭ и ОГЭ в учебном центре Резольвента

      Желающие ознакомиться с примерами решения различных задач по теме «Проценты» и применением процентов в экономике и финансовой математике могут посмотреть разделы нашего справочника «Проценты. Решение задач на проценты», «Простые и сложные проценты. Предоставление кредитов на основе процентной ставки», а также наши учебные пособия «Задачи на проценты» и «Финансовая математика».

      Приемы, используемые для решения задач на выполнение работ представлены в разделе нашего справочника «Задачи на выполнение работ».

      С примерами решения задач на смеси, сплавы и растворы можно ознакомиться в разделе нашего справочника «Задачи на смеси, сплавы и растворы».

       С демонстрационными вариантами ЕГЭ и ОГЭ, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.

Маркер СМИ

© 2007 — 2022 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель: Никитенко Евгений Игоревич

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

  • Альфашкола
  • Статьи
  • Вычисление средней скорости

Давайте разберем как вычислить среднюю скорость
Для этого надо сделать три шага:

  1.  вычислить весь путь;
  2.  вычислить время, за которое прошел объект  весь путь;
  3.  путь разделить на время;

Средняя скорость

Пример 1.  Саша прошел за 3 часа 9 км, а Сергей за 2 часа 6 км. Найдите их среднюю скорость.

Решение:   

(v_{ср}=frac{9+6}{3+2}=frac{15}{5}=3) км/час

Ответ: 3 км/час.

Пример 2. Пешеход прошел за 4 часа 10  км, а велосипедист  за 3 часа 11 км. Найдите их среднюю скорость.

Решение:   

(v_{ср}=frac{10+11}{4+3}=frac{21}{7}=3) км/час

Ответ: 3 км/час.

Пример 3.   Пароход проплыл за 2 часа со скоростью 20 км/ч и 3 часа со скоростью 30 км/ч. Вычислите среднюю скорость парохода.

Решение: 

  1. (2*20 + 3*30 = 40 +90 =130 ) (км) — весь путь .
  2. (2+3=5 ) (час) — все время.
  3. (130:5 =26 ) (км/час) — средняя скорость .

Ответ : 26 км/час.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!


Запишитесь на бесплатное тестирование знаний!

Как находить среднюю скорость в математике огэ

Репетитор по математике

Минский государственный лингвистический университет

Репетитор 1-11 классов.
Я люблю английский язык за его практичность, мелодичность звучания, пластичность и разнообразие слов. Использую игровые методы обучения, диалога, индивидуального подхода.

Как находить среднюю скорость в математике огэ

Репетитор по математике

Таганрогский педагогический институт им. А.П. Чехова

Репетитор 4-11 классов. Математика дисциплинирует и воспитывает ум, это основа для всех наук. Очень люблю работать с детьми! Уроки проходят в комфортной обстановке, к каждому ученику подхожу индивидуально, объясняю доступно и понятно. На занятиях применяю игровые приемы, схемы, графики и презентации, для того, чтобы учащимся было интересно.

Как находить среднюю скорость в математике огэ

Репетитор по математике

Санкт-Петербургский государственный университет аэрокосмического приборостроения

Репетитор 5-11 классов. Для меня математика — язык общения с миром. Всегда важно понимать, что стоит за той или иной цифрой, формулой, уравнением, понимать, какой смысл в себе они несут. Этому языку я обучаю своих учеников, помогаю полюбить его и научить умело применять в жизни. В преподавании основываюсь на том, чтобы закладывать основательные знания. Если фундамент прочный, то дальнейшее обучение всегда просто. Если есть трудности, то помогу найти и восполнить пробел. В каждом ученике я вижу личность и учитываю его индивидуальные особенности. В обучении использую идеи Льва Толстого. Преподаю с Любовью. Жду вас на своих уроках.

Средняя скорость – не самое сложное понятие в математике и физике. Однако простота этого понятия довольно часто оказывается обманчивой. Необходимо постоянно помнить, что средняя скорость – это величина, равная отношению пути, пройденного телом, ко времени, за которое пройден этот путь. Рассмотрим серию задач из открытого банка заданий по математике Федерального института педагогических измерений(ФИПИ) для проведения ОГЭ.

Задача 1. Первые 105 км автомобиль ехал со скоростью 35 км/ч, следующие 120 км — со скоростью 60 км/ч, а последние 500 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение. Чтобы найти среднюю скорость движения необходимо весь пройденный путь разделить на всё затраченное время. В задаче сказано о трёх участках пути, длина каждого известна. Найдём время движения на каждом участке.

105:35=3 (часа)

120:60=2 (часа)

500:100=5 (часов)

Всё затраченное время равно 3+2+5=10 час.

Длина пройденного пути 105+120+500=725 км.

Средняя скорость равна 725:10=72,5 км/час.

Ответ: 72,5

Задача 2. Первую половину пути автомобиль проехал со скоростью 69 км/ч, а вторую — со скоростью 111 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение. Обозначим весь пройденный путь через 2S. Тогда время затраченное на первую половину пути равно S/69, а на вторую S/111, всё затраченное время равно

S/69+ S/111=180S/(69*111).

Тогда средняя скорость равна 2S: 180S/(69*111)=2*69*111/180=85,1 км/час

Ответ: 85,1

Задача 3. Первые 2 часа автомобиль ехал со скоростью 45 км/ч, следующие 2 часа — со скоростью 35 км/ч, а последние 4 часа — со скоростью 105 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение. Чтобы найти среднюю скорость движения необходимо весь пройденный путь разделить на всё затраченное время.

Всё затраченное время равно 2+2+4=8 час.

Длина пройденного пути 45*2+35*2+105*4=580 км.

Средняя скорость равна 580:8=72,5 км/час.

Ответ: 72,5

 Задачи для самостоятельного решения.

1.      Первую половину трассы автомобиль проехал со скоростью 42 км/ч, а вторую — со скоростью 102 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

2.      Первую половину трассы автомобиль проехал со скоростью 52 км/ч, а вторую — со скоростью 78 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

3.      Первую половину трассы автомобиль проехал со скоростью 60 км/ч, а вторую — со скоростью 84 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

4.      Первую половину трассы автомобиль проехал со скоростью 36 км/ч, а вторую — со скоростью 108 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

5.      Первую половину трассы автомобиль проехал со скоростью 36 км/ч, а вторую — со скоростью 72 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

6.      Первую половину трассы автомобиль проехал со скоростью 78 км/ч, а вторую — со скоростью 91 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

7.      Первую половину трассы автомобиль проехал со скоростью 39 км/ч, а вторую — со скоростью 51 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

8.      Первую половину трассы автомобиль проехал со скоростью 30 км/ч, а вторую — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

9.      Первую половину трассы автомобиль проехал со скоростью 45 км/ч, а вторую — со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

10.  Первую половину трассы автомобиль проехал со скоростью 40 км/ч, а вторую — со скоростью 85 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

11.  Первую половину пути автомобиль проехал со скоростью 55 км/ч, а вторую — со скоростью 70 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

12.  Первую половину пути автомобиль проехал со скоростью 42 км/ч, а вторую — со скоростью 48 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

13.  Первую половину пути автомобиль проехал со скоростью 84 км/ч, а вторую — со скоростью 96 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

14.  Первую половину пути автомобиль проехал со скоростью 90 км/ч, а вторую — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

15.  Первую половину пути автомобиль проехал со скоростью 36 км/ч, а вторую — со скоростью 99 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

16.  Первую половину пути автомобиль проехал со скоростью 84 км/ч, а вторую — со скоростью 108 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

17.  Первую половину пути автомобиль проехал со скоростью 54 км/ч, а вторую — со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

18.  Первую половину пути автомобиль проехал со скоростью 34 км/ч, а вторую — со скоростью 51 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

19.  Первую половину пути автомобиль проехал со скоростью 60 км/ч, а вторую — со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

20.  Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

21.  Первые 2 часа автомобиль ехал со скоростью 80 км/ч, следующие 2 часа — со скоростью 50 км/ч, а последние 4 часа — со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

22.  Первые 4 часа автомобиль ехал со скоростью 50 км/ч, следующие 2 часа — со скоростью 90 км/ч, а последние 4 часа — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

23.  Первые 5 часов автомобиль ехал со скоростью 70 км/ч, следующие 3 часа — со скоростью 35 км/ч, а последние 2 часа — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

24.  Первые 5 часов автомобиль ехал со скоростью 100 км/ч, следующие 2 часа — со скоростью 50 км/ч, а последние 3 часа — со скоростью 55 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

25.  Первые 2 часа автомобиль ехал со скоростью 45 км/ч, следующие 4 часа — со скоростью 100 км/ч, а последние 2 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

26.  Первые 3 часа автомобиль ехал со скоростью 115 км/ч, следующие 2 часа — со скоростью 65 км/ч, а последние 4 часа — со скоростью 95 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

27.  Первые 5 часов автомобиль ехал со скоростью 110 км/ч, следующие 3 часа — со скоростью 50 км/ч, а последние 3 часа — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

28.  Первые 5 часов автомобиль ехал со скоростью 100 км/ч, следующие 3 часа — со скоростью 75 км/ч, а последние 2 часа — со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

29.  Первые 3 часа автомобиль ехал со скоростью 100 км/ч, следующие 4 часа — со скоростью 95 км/ч, а последние 3 часа — со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

30.  Первые 2 часа автомобиль ехал со скоростью 70 км/ч, следующие 3 часа — со скоростью 60 км/ч, а последние 5 часов — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

31.  Первые 5 часов автомобиль ехал со скоростью 55 км/ч, следующие 5 часов — со скоростью 75 км/ч, а последние 5 часов — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

32.  Первые 5 часов автомобиль ехал со скоростью 85 км/ч, следующие 5 часов — со скоростью 65 км/ч, а последние 5 часов — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

33.  Первые 2 часа автомобиль ехал со скоростью 65 км/ч, следующие 4 часа — со скоростью 105 км/ч, а последние 4 часа — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

34.  Первые 3 часа автомобиль ехал со скоростью 110 км/ч, следующие 3 часа — со скоростью 35 км/ч, а последние 3 часа — со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

35.  Первые 5 часов автомобиль ехал со скоростью 90 км/ч, следующие 2 часа — со скоростью 115 км/ч, а последние 3 часа — со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

36.  Первые 4 часа автомобиль ехал со скоростью 50 км/ч, следующие 4 часа — со скоростью 80 км/ч, а последние 4 часа — со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

37.  Первые 2 часа автомобиль ехал со скоростью 70 км/ч, следующие 3 часа — со скоростью 65 км/ч, а последние 3 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

38.  Первые 3 часа автомобиль ехал со скоростью 35 км/ч, следующие 2 часа — со скоростью 60 км/ч, а последние 5 часов — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

39.  Первые 90 км автомобиль ехал со скоростью 45 км/ч, следующие 400 км — со скоростью 100 км/ч, а последние 150 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

40.  Первые 345 км автомобиль ехал со скоростью 115 км/ч, следующие 130 км — со скоростью 65 км/ч, а последние 380 км — со скоростью 95 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

41.  Первые 550 км автомобиль ехал со скоростью 110 км/ч, следующие 150 км — со скоростью 50 км/ч, а последние 180 км — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

42.  Первые 500 км автомобиль ехал со скоростью 100 км/ч, следующие 225 км — со скоростью 75 км/ч, а последние 100 км — со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

43.  Первые 300 км автомобиль ехал со скоростью 100 км/ч, следующие 380 км — со скоростью 95 км/ч, а последние 150 км — со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

44.  Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 180 км — со скоростью 60 км/ч, а последние 225 км — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

45.  Первые 275 км автомобиль ехал со скоростью 55 км/ч, следующие 375 км — со скоростью 75 км/ч, а последние 400 км — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

46.  Первые 425 км автомобиль ехал со скоростью 85 км/ч, следующие 325 км — со скоростью 65 км/ч, а последние 300 км — со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

47.  Первые 130 км автомобиль ехал со скоростью 65 км/ч, следующие 420 км — со скоростью 105 км/ч, а последние 320 км — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

48.  Первые 90 км автомобиль ехал со скоростью 45 км/ч, следующие 70 км — со скоростью 35 км/ч, а последние 420 км — со скоростью 105 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

49.  Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

50.  Первые 160 км автомобиль ехал со скоростью 80 км/ч, следующие 100 км — со скоростью 50 км/ч, а последние 360 км — со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

51.  Первые 200 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а последние 180 км — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

52.  Первые 350 км автомобиль ехал со скоростью 70 км/ч, следующие 105 км — со скоростью 35 км/ч, а последние 160 км — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

53.  Первые 500 км автомобиль ехал со скоростью 100 км/ч, следующие 100 км — со скоростью 50 км/ч, а последние 165 км — со скоростью 55 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

54.  Первые 330 км автомобиль ехал со скоростью 110 км/ч, следующие 105 км — со скоростью 35 км/ч, а последние 150 км — со скоростью 50 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

55.  Первые 450 км автомобиль ехал со скоростью 90 км/ч, следующие 230 км — со скоростью 115 км/ч, а последние 120 км — со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

56.  Первые 200 км автомобиль ехал со скоростью 50 км/ч, следующие 320 км — со скоростью 80 км/ч, а последние 140 км — со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

57.  Первые 140 км автомобиль ехал со скоростью 70 км/ч, следующие 195 км — со скоростью 65 км/ч, а последние 225 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Добрый день, друзья! Продолжаем подготовку к экзаменам по математике. И сегодня на очереди задачи на среднюю скорость.
Эти задачи достаточно просты, однако в них есть некоторая изюминка, которая поддаётся далеко не всем.
Остановимся на ней подробнее.
Мы знаем, что расстояние, это произведение скорости на пройденное время.
 Также, скорость — это расстояние, делённое на время, а время — это расстояние, делённое на скорость.
Поэтому, когда разговор идёт о средней скорости, ни в коем случае НЕЛЬЗЯ просто сложить эти скорости и разделить на количество пройденных отрезков. Необходимо такие задачи решать с учётом пройденного расстояния и затраченного времени.
Давайте разберём это подробнее в примерах.
Пример 1. Первые 300 км автомобиль ехал со скоростью 60 км/час, следующие 315 км со скоростью 90 км/час и последние 120 км со скоростью 80 км/час. Необходимо найти среднюю скорость автомобиля на протяжении всего пути.
Решение: было бы совершенно неправильно сложить значения трех скоростей и разделить на 3.
Всё дело в том, что автомобиль ехал разное расстояние на каждом из отрезков, поэтому, необходимо вычислить общее расстояние, которое он прошёл и общее затраченное им время.
После этого мы можем найти среднюю скорость, разделив расстояние на время.
t1 = 300/60 = 5 часов
t2 = 315/90 = 3,5 часа
t3 = 120/80 = 1,5 часа
Итого, общее время поездки составило 5+3,5+1,5 = 10 часов.
Расстояние, которое проехал автомобиль за это время:
300+315+120 = 735 км.
Средняя скорость равна 735/10 = 73,5 км/час.
Ответ: средняя скорость автомобиля 73,5 км/час.
Пример 2. Из пункта А в пункт В, расстояние между которыми 84 км, одновременно выехали автомобилист и велосипедист.
Известно, что за 1 час автомобилист проезжает на 48 км больше,
чем велосипедист.
Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 5 часов 36 минут позже автомобилиста.
Решение: В данной задаче необходимо свести в одну формулу выражения S, v, t для автомобилиста и велосипедиста.
Пусть скорость велосипедиста Х,
тогда, расстояние в 84 км он прошёл за 84/Х часов.
Скорость автомобилиста  на 48 км больше, чем скорость велосипедиста, значит она равна Х+48.
Время, за которое автомобилист прошёл расстояние в 84 км,
равно 84/(Х+48) часов.
По условию задачи сказано, что велосипедист прибыл в пункт В
 на 5 часов 36 минут позже, т.е. он затратил время на 5 36/60 часа больше,
или на 5,6 часа.
Составляем уравнение:
84/Х — 84/(Х+48) = 5,6  Сокращаем числители правой и левой части уравнения на 5,6
15/Х — 15/(Х+48) = 1
15Х + 720 — 15Х = Х² + 48Х
Х² + 48Х — 720 = 0    Решая уравнения с помощью теоремы Виета,
находим корни:
Х1 = 12;
Х2 = -60  не подходит по смыслу.
Ответ: скорость велосипедиста равна 12 км/час.
Пример 3. Из разных городов, расстояние между которыми 600 км, одновременно навстречу друг другу выехали два автомобиля.
Скорость первого на 15 км/час меньше, чем скорость второго.
Второй автомобиль прибыл в конечный пункт на 1 час 20 минут раньше, чем первый.
Найдите скорость второго автомобиля.
Решение: Пусть скорость второго автомобиля будет Х км/час,
тогда скорость первого — (Х-15) км/час.
Второй автомобиль затратил на всю дорогу  600/Х часов,
а первый — 600/(Х-15) часов.
Причем, первый автомобиль ехал дольше на 1 час 20 минут,
 или на 1  1/3 часа.
Составляем уравнение:
600/(Х-15) — 600/Х = 4/3  Сокращаем числители дробей на 4.
150/(Х-15) — 150/Х = 1/3
450Х — 450Х + 6750 = Х² — 15Х
Х² — 15Х — 6750 = 0 Применяя общее решение уравнения через дискриминант, получим:
Х1 = 90
Х2 = -75  не подходит по смыслу задачи.
Ответ: скорость второго автомобиля равна 90 км/час.
Пример 4. Водитель ехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 240 км.
Отправившись обратно в А, от увеличил скорость на 20 км/час.
По пути он сделал остановку на 1 час, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в Б.
 Найти скорость машины из А в Б.
Решение: Пусть скорость автомобиля из А в Б равна Х.
Тогда от затратил на прохождение 240 км   240/Х часов.
Обратно его скорость была Х+20 км/час.
И время, за которое  он прошёл 240 км, равно 240/(Х+20).
Причем, обратно он ехал на 1 час меньше.
Составляем уравнение:
240/Х — 240/(Х+20) = 1
240Х + 4800 — 240Х = Х² + 20Х
Х² + 20Х — 4800 = 0
Решаем через дискриминант с чётным вторым коэффициентом:
Х1,2 = -10 ±√(10² + 4800) = -10 ±√4900 = -10 ±70.
Х1 = -10 + 70 = 60
Х2 = -10 — 70 = — 80 не подходит по смыслу задачи.
Ответ: Скорость автомобиля на пути из А в Б равна 60 км/час.
На сегодня. всё.
Успехов и до новых задач!

Источник

Задачи ЕГЭ на нахождение средней скорости

На экзамене по математике вам может также встретиться задача о нахождении средней скорости. Запомним, что средняя скорость не равна среднему арифметическому скоростей. Она находится по специальной формуле:

v_{cp}=genfrac{}{}{}{0}{displaystyle S_o}{displaystyle t_o},

где v_{cp} — средняя скорость, S_o— общий путь, t_o — общее время.

Если участков пути было два, то
v_{cp}=genfrac{}{}{}{0}{displaystyle S_1 + S_2}{displaystyle t_1+t_2}

1. Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

Мы не знаем, каким было расстояние, которое преодолел путешественник. Знаем только, что это расстояние было одинаковым на пути туда и обратно. Для простоты примем это расстояние за 1 (одно море). Тогда время, которое путешественник плыл на яхте, равно genfrac{}{}{}{0}{displaystyle 1}{displaystyle 20}, а время, затраченное на полет, равно genfrac{}{}{}{0}{displaystyle 1}{displaystyle 480}. Общее время равно genfrac{}{}{}{0}{displaystyle 1}{displaystyle 20}+genfrac{}{}{}{0}{displaystyle 1}{displaystyle 480}=genfrac{}{}{}{0}{displaystyle 25}{displaystyle 480}=genfrac{}{}{}{0}{displaystyle 5}{displaystyle 96}.

Средняя скорость равна  38,4  км/ч.

Ответ: 38,4.

2. Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Средняя скорость – это вовсе не среднее арифметическое скоростей. По определению,

Найдем S_1, S_2 и S_3 по формуле: S_ =vt.

Получим, что S_1=50cdot 2=100 км, S_2=1000cdot 1=100 км, S_3=75cdot 2=150 км,

км.

Ответ: 70.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи ЕГЭ на нахождение средней скорости» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти напольную плитку по фото
  • Как найти микрозайм по номеру телефона
  • Как найти напряженность электрического поля внутри конденсатора
  • Как найти дневники диппера
  • Как найти ставку организации

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии