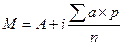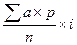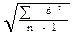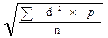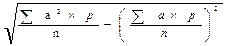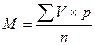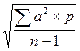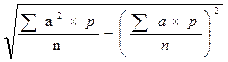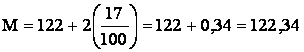«Способ
моментов»
применяется в рядах с равными интервалами
на основе свойств средней арифметической.
Средняя арифметическая исчисляется по
формуле
,
где i
– размер интервала;
m1
– момент первого порядка (средняя
арифметическая из новых упрощенных
вариант
;
– новые упрощенные варианты;f
– частота);
А– постоянное
число (лучше всего взять его равным
варианте, у которой наибольшая частота).
Определим среднее
значение признака «способом моментов»
на следующем примере.
Пример 5. Имеются
следующие данные о распределении
магазинов облпотребсоюза по торговой
площади (табл. 14).
Таблица 14
|
Группировка |
Удельный |
|
До 40 |
5 |
|
40–60 |
30 |
|
60–80 |
40 |
|
80–100 |
20 |
|
Свыше 100 |
5 |
|
Итого |
100 |
Следует определить
среднюю площадь магазинов, применив
«способ моментов».
Решение
Данные
распределения магазинов по торговой
площади представлены в виде интервального
ряда распределения с равными интервалами
(i =
20 м2),
следовательно, расчет средней площади
магазина можно
провести по формуле
,
применив «способ моментов».
Первый
и последний интервалы даны открытыми,
т. е. не имеют границ нижней и верхней
соответственно. Для определения среднего
значения в них границы интервалов
следует закрыть. Для первой группы с
размером площади до 40 м2
условно считаем, что интервал также
равен 20 м2,
затем вычитаем 20 м2
из 40 м2
и находим условную
нижнюю границу первого интервала (20 –
40). Условную верхнюю
границу последнего интервала определяем
аналогично (100
– 120).
Расчеты следует
проводить в табл. 15.
Таблица 15
|
Группировка |
Удельный |
Середина |
х |
|
xf |
|
20–40 |
5 |
30 |
–40 |
–2 |
–10 |
|
40–80 |
30 |
50 |
–20 |
–1 |
–30 |
|
60–80 |
40 |
70 |
0 |
0 |
0 |
|
80–100 |
20 |
90 |
20 |
1 |
20 |
|
100–120 |
5 |
110 |
40 |
2 |
10 |
|
Итого |
100 |
– |
– |
– |
–10 |
Наибольшая
частота f
равна 40, следовательно, в качестве
постоянной величины А
принимаем 70.
Определяем
момент первого порядка:
.
Среднее
значение признака равно:
+ 70 =
= 68 м2.
Следовательно,
средняя площадь магазина составляет
68 м2.
5.3. Структурные средние
В
качестве структурных средних чаще всего
используют показатели моды и медианы.
Мода
(Мо)
– наиболее часто повторяющееся значение
признака. Медиана
(Ме)
– величина признака, которая делит
упорядоченный ряд на две равные по
численности части.
Если расчет моды
и медианы проводится в дискретном ряду,
то он опирается на их понятия. В
интервальном ряду распределения для
расчета моды и медианы применяют
следующие формулы.
Мода рассчитывается
по формуле
,
где
хМо
– нижнее значение модального интервала;
iМо
– размер модального интервала;
fМо
– частота модального интервала;
fМо–1
– частота, предшествующая модальной
частоте;
fМо+1
– частота, последующая за модальной
частотой.
Модальному интервалу
соответствует наибольшая (модальная)
частота. Медиана рассчитывается по
формуле
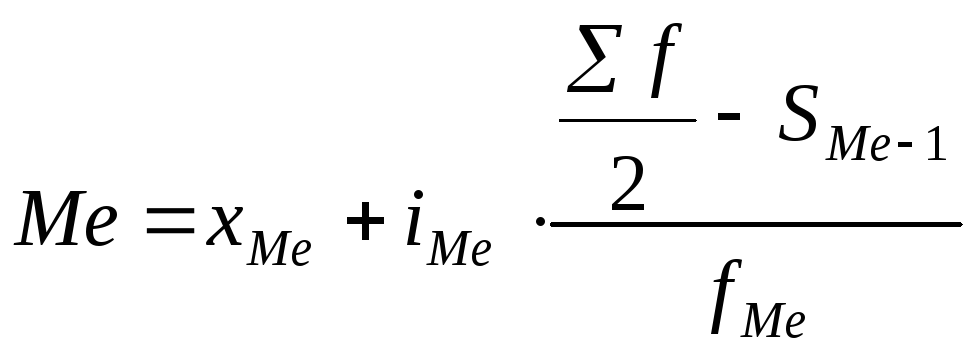
где
хМе
– нижнее значение медианного интервала;
iМе
– размер медианного интервала;
f
– сумма частот;
SМе–1
– сумма частот, предшествующих медианной
частоте;
fМе
– медианная частота.
Медианному
интервалу соответствует медианная
частота. Таким интервалом будет интервал,
сумма накопленных частот которого равна
или превышает половину суммы всех
частот.
Рассмотрим
определение моды и медианы на следующих
примерах.
Пример 6. В
результате статистического обследования
области получены следующие данные по
распределению семей по числу детей
(табл. 16).
Таблица 16
|
Число |
Количество |
|
0 |
5 |
|
1 |
32 |
|
2 |
34 |
|
3 |
16 |
|
4 |
6 |
|
5 |
4 |
|
6 и более |
3 |
|
Итого |
100 |
Следует определить
моду и медиану.
Решение
В дискретных рядах
модой является варианта с наибольшей
частотой. Наибольшая частота – 34,
следовательно мода равна 2.
Для
вычисления медианы определим сумму
частот ряда (f
= 100), затем рассчитаем полусумму
.
Так
как сумма накопленных частот 5 + 32 + 34 =
71 превышает полусумму
(71 > 50), то варианта, имеющая значение
2 и соответствующая
этой накопленной сумме частот, и есть
медиана.
Пример 7. В
результате статистического обследования
получены следующие данные распределения
продавцов магазинов облпотребсоюза по
возрасту (табл. 17).
Таблица 17
|
Группировка |
Удельный |
|
До 20 |
6 |
|
20–30 |
24 |
|
30–40 |
35 |
|
Окончание |
|
|
Группировка |
Удельный |
|
40–50 |
26 |
|
Свыше 50 |
9 |
|
Итого |
100 |
Необходимо
определить моду и медиану.
Решение
В интервальных
рядах мода и медиана определяются по
вышеприведенным формулам.
Сначала
определим модальный интервал, он
соответствует наибольшей частоте. Так
как наибольшая частота равна 35 и является
модальной, то интервал 30–40 является
модальным интервалом. Затем подставим
данные в следующую формулу:
лет.
Определим
медианный интервал. Полусумма частот
равна 50
.
Накапливая частоты, определим интересующий
интервал. Так как сумма накопленных
частот 6 + 24 + 35 = 65 превышает полусумму
(65 > 50), значит 35 является медианной
частотой, а интервал 30–40 является
медианным интервалом.
Затем подставим
данные в формулу
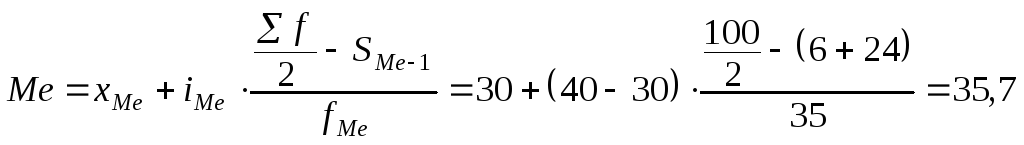
Таким образом,
мода равна 35,5 лет (больше всего продавцов
в возрасте 35,5 лет), медиана – 35,7 лет
(50 % продавцов достигли возраста 35,7 лет).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Вычисление средней арифметической по способу моментов
- Статистические величины. Использование их в медицине. Динамические ряды. Способы их выравнивания и анализа: Учебно-методическое пособие , страница 3
- 5.2. Вычисление средней из вариационного ряда «способом моментов»
- Способ моментов
Вычисление средней арифметической по способу моментов
При большом числе наблюдений или при большом числовом значении вариант применяют
упрощенный способ вычисления средней арифметической- способ моментов.
где М — средняя арифметическая; А — условная средняя; i — интервал между группами вариант;
S — знак суммирования.; а- условное отклонение каждой варианты от условной средней;
р — частота встречаемости вариант; n — число наблюдений.
Пример вычисления средней арифметической по способу моментов (средней массы тела
юношей в возрасте 18 лет)
| V(n в кг) | Р | а (V-А) | а . Р |
| +2 | +4 | ||
| +1 | +3 | ||
| Мо=62 | |||
| -1 | -6 | ||
| -2 | -8 | ||
| -3 | -3 | ||
| п = 25 | Sар = — 10кг |
Этапы расчета средней по способу моментов:
1) за условную среднюю А рекомендуется принять Моду или Медиану, например А = 62кг, так как 62 кг было у 9 юношей из 25;
2) определяем «а» — условное отклонение варианты от условной средней, для этого из каждой варианты вычитаем условную среднюю: а = V — А, ( например, а = 64 — 62 = +2 и т.д.).
3) умножаем условное отклонение «а» на частоту «р» каждой варианты и получаем произведение а р;
4) находим сумму Sа . р = — 10кг
5) рассчитываем среднюю арифметическую по способу моментов:
М = А + i SаР = 62 — 1×0,4 = 61,6кг
Таким образом, можно сделать вывод, что в изучаемой нами группе юношей средняя масса тела
Средняя арифметическая сама по себе ничего не говорит о том вариационном ряде, из которого
она была вычислена. На ее типичность (достоверность) влияет однородность рассматриваемого
материала и колеблемость ряда.
Пример: даны два одинаковых по числу наблюдений вариационных ряда, в которых
представлены данные измерений окружности головы детей в возрасте от 1 года до 2-х лет
| Ряд 1 | Ряд 2 | |
| Окружность головы(в см) Частота | 41, 45, 46, 47, 48 7, 8, 25, 6, 2 | 42, 43, 44, 45, 46, 47, 48, 49, 50 1, 2, 4, 6, 14, 10, 3, 0, 2 |
Имея одинаковое число наблюдений и одинаковые средние арифметические (М= 46 см), ряды
имеют различия в распределении внутри. Так варианты первого ряда отклоняются в целом от
средней арифметической с меньшим значением, чем варианты второго ряда, что дает
возможность предположить, что средняя арифметическая (46 см) более типична для первого
ряда, чем для второго.
В статистике для характеристики разнообразия вариационного ряда употребляют среднее
квадратическое отклонение (s)
Существует два способа расчета среднего квадратического отклонения: среднеарифметический
способ и способ моментов. При среднеарифметическом способе расчета применяют формулу:
где d истинное отклонение каждой варианты от истиной средней М. Формула используется при
Источник
Статистические величины. Использование их в медицине. Динамические ряды. Способы их выравнивания и анализа: Учебно-методическое пособие , страница 3
В чётных вариационных рядах сумма частот или общее число наблюдений выражено чётным числом, в нечётных ― нечётным.
5. Симметричные и асимметричные.
В симметричном вариационном ряду все виды средних величин совпадают или очень близки (мода, медиана, среднее арифметическое).
В зависимости от характера изучаемых явлений, от конкретных задач и целей статистического исследования, а также от содержания исходного материала, в санитарной статистике применяются следующие виды средних величин:
· структурные средние (мода, медиана);
Мода (Мо) — величина варьирующего признака, которая более часто встречается в изучаемой совокупности т.е. варианта, соответствующая наибольшей частоте. Находят ее непосредственно по структуре вариационного ряда, не прибегая к каким-либо вычислениям. Она обычно является величиной очень близкой к средней арифметической и весьма удобна в практической деятельности.
Медиана (Ме) — делящая вариационный ряд (ранжированный, т.е. значения вариант располагаются в порядке возрастания или убывания) на две равные половины. Медиана вычисляется при помощи так называемого нечетного ряда, который получают путем последовательного суммирования частот. Если сумма частот соответствует четному числу, тогда за медиану условно принимают среднюю арифметическую из двух средних значений.
Мода и медиана применяются в случае незамкнутой совокупности, т.е. когда наибольшая или наименьшая варианты не имеют точной количественной характеристики (например, до 15 лет, 50 и старше и т.п.). В этом случае среднюю арифметическую (параметрические характеристики) рассчитать нельзя.
Средняя арифметическая — самая распространенная величина. Средняя арифметическая обозначается чаще через М.
Различают среднюю арифметическую простую и взвешенную.
Средняя арифметическая простая вычисляется:
― в тех случаях, когда совокупность представлена простым перечнем знаний признака у каждой единицы;
― если число повторений каждой варианты нет возможности определить;
― если числа повторений каждой варианты близки между собой.
Средняя арифметическая простая исчисляется по формуле:
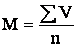
где V — индивидуальные значения признака; n — число индивидуальных значений; 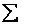
Таким образом, простая средняя представляет собой отношение суммы вариант к числу наблюдений.
Пример: определить среднюю длительность пребывания на койке 10 больных пневмонией:
16 дней — 1 больной; 17–1; 18–1; 19–1; 20–1; 21–1; 22–1; 23–1; 26–1; 31–1.
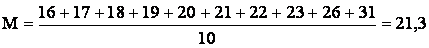
Средняя арифметическая взвешенная исчисляется в тех случаях, когда индивидуальные значения признака повторяются. Ее можно вычислять двояким способом:
1. Непосредственным (среднеарифметическим или прямым способом) по формуле:
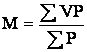
где P — частота (число случаев) наблюдений каждой варианты.
Таким образом, средняя арифметическая взвешенная представляет собой отношение суммы произведений вариант на частоты к числу наблюдений.
2. С помощью вычисления отклонений от условной средней (по способу моментов).
Основой для вычисления взвешенной средней арифметической является:
― сгруппированный материал по вариантам количественного признака;
― все варианты должны располагаться в порядке возрастания или убывания величины признака (ранжированный ряд).
Для вычисления по способу моментов обязательным условием является одинаковый размер всех интервалов.
По способу моментов средняя арифметическая вычисляется по формуле:

где Мо — условная средняя, за которую чаще принимают величину признака, соответствующую наибольшей частоте, т.е. которая чаще повторяется (Мода).
i — величина интервала.
a — условное отклонение от условий средней, представляющее собой последовательный ряд чисел (1, 2 и т.д.) со знаком + для вариант больших условной средней и со знаком–(–1, –2 и т.д.) для вариант, которые ниже условной средней. Условное же отклонение от варианты, принятой за условную среднюю равно 0.
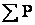
Пример: определить средний рост мальчиков 8 лет непосредственным способом (таблица1).
Источник
5.2. Вычисление средней из вариационного ряда «способом моментов»
«Способ моментов» применяется в рядах с равными интервалами на основе свойств средней арифметической. Средняя арифметическая исчисляется по формуле
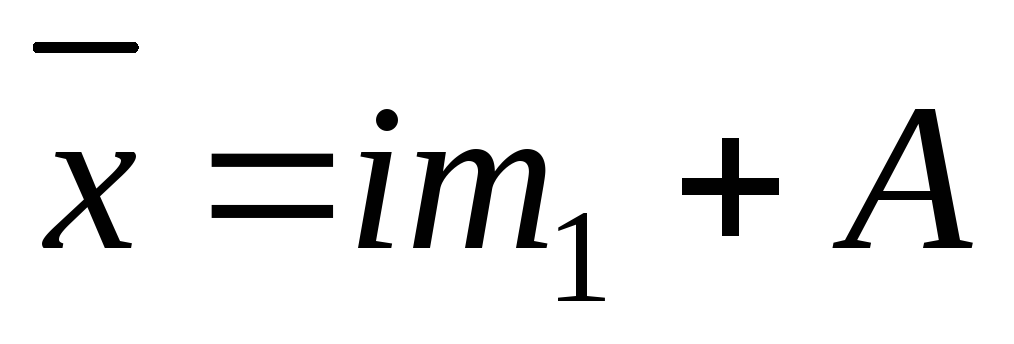
где i – размер интервала;
m1 – момент первого порядка (средняя арифметическая из новых упрощенных вариант 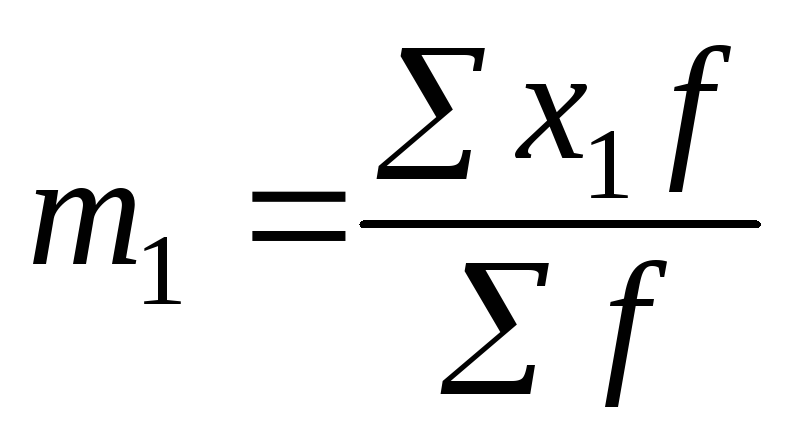
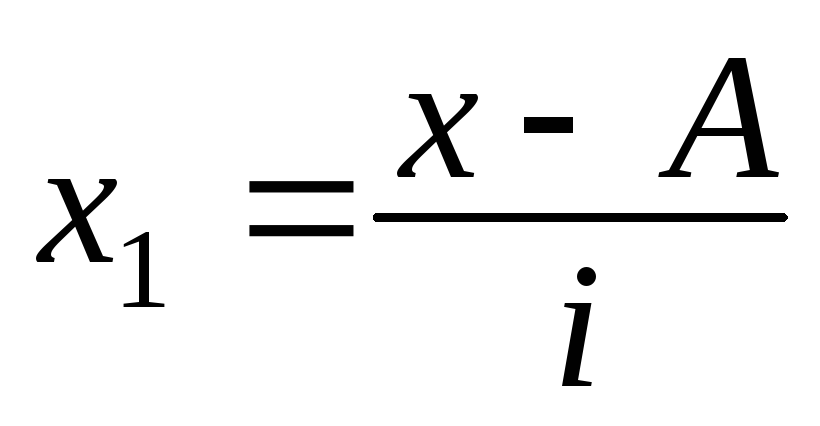
А– постоянное число (лучше всего взять его равным варианте, у которой наибольшая частота).
Определим среднее значение признака «способом моментов» на следующем примере.
Пример 5. Имеются следующие данные о распределении магазинов облпотребсоюза по торговой площади (табл. 14).
Группировка магазинов по торговой площади, м 2 (х)
Удельный вес магазинов, % ( f )
Следует определить среднюю площадь магазинов, применив «способ моментов».
Данные распределения магазинов по торговой площади представлены в виде интервального ряда распределения с равными интервалами (i = 20 м 2 ), следовательно, расчет средней площади магазина можно провести по формуле 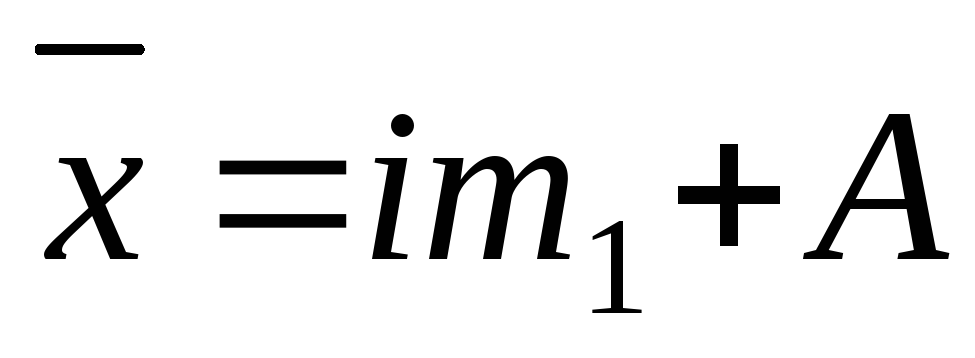
Первый и последний интервалы даны открытыми, т. е. не имеют границ нижней и верхней соответственно. Для определения среднего значения в них границы интервалов следует закрыть. Для первой группы с размером площади до 40 м 2 условно считаем, что интервал также равен 20 м 2 , затем вычитаем 20 м 2 из 40 м 2 и находим условную нижнюю границу первого интервала (20 – 40). Условную верхнюю границу последнего интервала определяем аналогично (100 – 120).
Расчеты следует проводить в табл. 15.
Группировка мага- зинов по торговой площади, м 2 (х)
Источник
Способ моментов



Применяя этот способ, среднюю арифметическую рассчитывают по формуле:
Эта формула технически упрощает расчеты, особенно в тех случаях, когда варианты состоят из многозначных чисел, а совокупность — из большого числа наблюдений.
Например: Методика расчета средней арифметической величины по способу моментов Таблица 8.
| V кг | p | а | а ×р |
| 64 | 2 | +2 | +4 |
| 63 | 3 | +1 | +3 |
| 62 | 9 | 0 | 0 |
| 61 | 6 | -1 | -6 |
| 60 | 4 | -2 | -8 |
| 59 | 1 | -3 | -3 |
| n =25 | Sа × р = -10 кг |
Этапы расчета М по способу моментов:
1) за условную среднюю Ао рекомендуется принять варианту, чаще других повторяющуюся в вариационном ряду. В нашем примере: Ао = М = 62 кг., так как 62 кг было у 9 юношей из 25;
2) определяем а — условное отклонение от условной средней. Для этого из каждой варианты вычитаем условную среднюю а = (V — Ао).
В нашем примере: а = 64 — 62 = + 2 и т. д.;
3) умножаем условное отклонение (а) на частоту (р) каждой варианты и получаем произведения
(а × р).
В нашем примере: 2 ×(+2) = 4 и т.д.
4) получаем сумму S а × р
В нашем примере: — 10кг;
5) определяем интервал между группами вариант ( I)
В нашем примере: i = 1 кг;
6) момент первой степени
В нашем примере: -10 кг / 25× 1 = — 0,4
7)рассчитываем среднюю арифметическую по способу моментов:
В нашем примере: М = 62 кг – 0,4 = 61,6 кг
Есливариационный ряд предварительно был сгруппирован, то в качестве ряда(V)используются середины групп.
Средняя арифметическая величина обладает тремя свойствами.
1. Средняя занимает серединное положение в вариационном ряду. В строго симметричном ряду: М = Мо = Ме.
2. Средняя является обобщающей величиной и за ней не видны колебания, различия индивидуальных данных.
3. Сумма отклонений всех вариант от средней равна нулю. Sd = S (V-M) = 0
Величина того или иного признака неодинакова у всех членов совокупности, несмотря на ее относительную однородность.
Наиболее полную характеристику разнообразию признака в совокупности дает так называемое среднее квадратическое отклонение, обозначаемое греческой буквой «сигма» — s.
Существует два способа расчета среднего квадратического отклонения: среднеарифметический и способ моментов. При среднеарифметическом способе расчета применяют формулу: s =
где d— истинное отклонение вариант от истинной средней (V-М). Эта формула используется при небольшом числе наблюдений (n 1 используют формулу такого вида:
s = 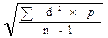
При Р>1 и N>30 — s =
Следующая формула предназначена для определения s по способу моментов: s =i×
где а — условное отклонение вариант от условной средней: а =V — А; Sa 2 ×p/n момент второй степени, а (Sa×p/n) 2 — момент первой степени, возведённый в квадрат. Этот способ применяется в тех случаях, когда нет вычислительной техники, а вариационный ряд громоздкий как за счет большого числа наблюдений, так и за счет вариант, выраженных многозначными числами. При числе наблюдений, равном 30 и менее, в моменте второй степени n заменяют на (n-1).
Например: Расчет среднего квадратического отклонения по среднеарифметическому способу. Таблица 9.
| Рост мальчиков 12 лет. | Число детей (р) | V • Р | d | d 2 | d 2 × Р |
| 155 | 1 | 155 | +2 | 4 | 4 |
| 154 | 4 | 616 | +1 | 1 | 4 |
| 153 | 6 | 918 | 0 | 0 | 0 |
| 152 | 4 | 608 | —1 | 1 | 4 |
| 151 | 1 | 151 | —2 | 4 | 4 |
| М = 153 | n = 16 | SV ×p = 1448 | S d 2 × Р = 16 |
Последовательность расчета s.
1.Определить М (по среднеарифметическому способу).
В нашем примере: 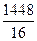
2.Найти истинное отклонение d =(V-M).
В нашем примере:155-153=+2; 154-153= +1 и т.д.
3.Возвести каждое отклонение в квадрат d 2.
4.Найти произведение (d 2 × р) по всем строкам ряда.
5.Определить сумму (S d 2 ×р).
В нашем примере: 4+4+0+4+4=16
6.Рассчитать s по формуле:
В нашем примере: Ö16/16-1 =1,05 см. 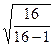
Например: Расчет среднего квадратического отклоненияпо способу моментов Таблица 10.
| Рост, см (V) | Число детей (р) | а | а×р а×р | a 2 ×р |
| 155 | 1 | +2 | 2 | 4 |
| 154 | 4 | + 1 | 4 | 4 |
| 153 | 6 | 0 | 0 | 0 |
| 152 | 4 | -1 | -4 | 4 |
| 151 | 1 | -2 | -2 | 4 |
| n = 16 | Sар = 0 | Sa 2 ×р = 16 |
Последовательность расчета s по способу моментов.
1.Найти условную среднюю А
В нашем примере: А =153 cм.
2.Определить условное отклонение (а) каждой варианты от условной средней: а =V — А.
3.Получить произведения а × р, а затем их просуммировать.
В нашем примере: =0.
4.Рассчитать истинную среднюю арифметическую по формуле
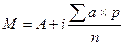
5.Получить произведения а 2 ×p по всем строкам вариационного ряда и просуммировать их.

В нашем примере:Sa 2 ×p =16.
6. Рассчитать по способу моментов по формуле: s =i×
В нашем примере:s =1× 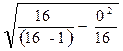
Ошибка репрезентативности (m) является важнейшей статистической величиной, необходимой для оценки достоверности результатов исследования. Эта ошибка возникает в тех случаях, когда требуется по части охарактеризовать явление в целом. Эти ошибки неизбежны. Они проистекают из сущности выборочного исследования: генеральная совокупность может быть охарактеризована по выборочной совокупности только с некоторой погрешностью, измеряемой ошибкой репрезентативности.
По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном наблюдении, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования всех без исключения элементов генеральной совокупности.
Ошибки репрезентативности можно свести к достаточно малой величине, т. е. к величине допустимой погрешности. Делается это путем привлечения в выборку достаточного количества наблюдений (n):
· 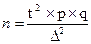
· 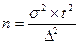
p– вероятность наступления явления (выбирается по данным аналогичных исследований)
q— вероятность не наступления явления, q =100-p
t— доверительный критерий – таблица 11.
D— предельная ошибка, вытекает из таблицы 6, исходя из выбранного t.
| Степень безошибочного прогноза (Р) | Доверительный критерий (t) | Предельная ошибка (D) |
| 68% | — | |
| 95% | 5% | |
| 99% | 1% |
Если аналогичных исследований нет, то p и q принимаются как 50% на 50%.
Ошибки репрезентативности рассчитываются по следующим формулам:
· 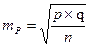
· 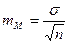
В медицине и здравоохранении по разности параметров оценивают средние и относительные величины, полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т. д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность. Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности. Достоверность различия сравниваемых величин измеряется доверительным критерием (критерием точности t), который рассчитывается по специальным формулам для средних и относительных величин.
Формула оценки достоверности разности сравниваемых величин такова:
· 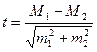
· 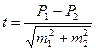
Разность величин считается достоверной при значениях, равных или больших 2. Р1 всегда выбирается больше, чем Р2.
Например: При изучении влияния анаболических гормонов при инфаркте миокарда на белковый обмен были получены следующие данные: общий белок до лечения (Р) составил 7,14% (m-±0,17%), после лечения (Р) 8,04% (m-±0,12%).
1. Определяем большую величину как Р1, а меньшую как Р2.
2.Возводим ошибки репрезентативности в квадраты:
В нашем примере: 0,17 2 =0,0289;0,12 2 = 0,0144.
3.Складываем квадраты и извлекаем квадратный корень.
В нашем примере: Ö0,0289+0,0144=Ö0,0433 = 0,2.
4.Находим разность сравниваемых величин и делим на знаменатель.
В нашем примере:8,04-7,14=0,9/0,2=4,5.
В нашем примере: 4,5>2, значит разность величин достоверна, т.е, анаболические гормоны действительно увеличивают уровень общего белка.
Источник
4. Четные и нечетные.
В чётных вариационных рядах сумма частот или общее
число наблюдений выражено чётным числом, в нечётных ― нечётным.
5.
Симметричные и асимметричные.
В
симметричном вариационном ряду все виды средних величин совпадают или очень
близки (мода, медиана, среднее арифметическое).
В
зависимости от характера изучаемых явлений, от конкретных задач и целей
статистического исследования, а также от содержания исходного материала, в
санитарной статистике применяются следующие виды средних величин:
· структурные
средние (мода, медиана);
·
средняя арифметическая;
·
средняя гармоническая;
·
средняя геометрическая;
·
средняя прогрессивная.
Мода (Мо) — величина
варьирующего признака, которая более часто встречается в изучаемой совокупности
т.е. варианта, соответствующая наибольшей частоте. Находят ее непосредственно
по структуре вариационного ряда, не прибегая к каким-либо вычислениям. Она
обычно является величиной очень близкой к средней арифметической и весьма удобна
в практической деятельности.
Медиана (Ме) —
делящая вариационный ряд (ранжированный, т.е. значения вариант располагаются в
порядке возрастания или убывания) на две равные половины. Медиана вычисляется
при помощи так называемого нечетного ряда, который получают путем
последовательного суммирования частот. Если сумма частот соответствует четному
числу, тогда за медиану условно принимают
среднюю арифметическую из двух средних значений.
Мода и медиана применяются в случае незамкнутой
совокупности, т.е. когда наибольшая или наименьшая варианты не имеют точной
количественной характеристики (например, до 15 лет, 50 и старше и т.п.). В этом
случае среднюю арифметическую (параметрические характеристики) рассчитать
нельзя.
Средняя арифметическая —
самая распространенная величина. Средняя арифметическая обозначается чаще через
М.
Различают
среднюю арифметическую простую и взвешенную.
Средняя арифметическая простая вычисляется:
― в тех случаях, когда совокупность представлена
простым перечнем знаний признака у каждой единицы;
― если число повторений каждой
варианты нет возможности определить;
― если числа повторений каждой варианты близки между
собой.
Средняя
арифметическая простая исчисляется по формуле:
,
где V — индивидуальные значения признака; n —
число индивидуальных значений; — знак суммирования.
Таким образом, простая средняя представляет собой
отношение суммы вариант к числу наблюдений.
Пример: определить среднюю длительность пребывания на
койке 10 больных пневмонией:
16 дней — 1 больной; 17–1; 18–1;
19–1; 20–1; 21–1; 22–1; 23–1; 26–1; 31–1.
койко-дня.
Средняя арифметическая взвешенная исчисляется
в тех случаях, когда индивидуальные значения признака повторяются. Ее можно
вычислять двояким способом:
1. Непосредственным (среднеарифметическим или прямым
способом) по формуле:
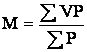
где P — частота (число случаев) наблюдений каждой варианты.
Таким образом, средняя арифметическая взвешенная
представляет собой отношение суммы
произведений вариант на частоты к числу наблюдений.
2. С помощью вычисления отклонений от условной средней (по способу моментов).
Основой для вычисления взвешенной средней
арифметической является:
― сгруппированный материал по
вариантам количественного признака;
―
все варианты должны располагаться в порядке возрастания или убывания величины
признака (ранжированный ряд).
Для вычисления по способу моментов обязательным
условием является одинаковый размер всех интервалов.
По способу
моментов средняя арифметическая вычисляется по формуле:

где Мо — условная средняя, за которую чаще
принимают величину признака, соответствующую
наибольшей частоте, т.е. которая чаще повторяется (Мода).
i — величина интервала.
a — условное отклонение от условий средней,
представляющее собой последовательный ряд чисел (1, 2 и т.д.) со знаком + для
вариант больших условной средней и со знаком–(–1, –2 и т.д.) для вариант,
которые ниже условной средней. Условное же отклонение от варианты, принятой за
условную среднюю равно 0.
P — частоты.
— общее
число наблюдений или n.
Пример: определить средний рост
мальчиков 8 лет непосредственным способом (таблица1).
Т а б л и ц а 1
|
Рост в см |
Число мальчиков P |
Центральная варианта V |
VP |
|
115-116 |
2 |
116 |
232 |
|
117-118 |
7 |
118 |
826 |
|
119-120 |
21 |
120 |
2520 |
|
121-122 |
33 |
122 |
4026 |
|
123-124 |
21 |
124 |
2604 |
|
125-126 |
12 |
126 |
1512 |
|
127-128 |
3 |
128 |
384 |
|
129-130 |
1 |
130 |
130 |
n = 100
12234
Центральная варианта ― середина интервала ― определяется
как полу сумма начальных значений двух соседних групп:
;
и т.д.
Произведение VP получают путем умножения центральных
вариант на частоты ;
и
т.д. Затем полученные произведения складывают и получают , которую делят на число наблюдений
(100) и получают среднюю арифметическую взвешенную.
см.
Эту же задачу решим по способу моментов, для чего
составляется следующая таблица 2:
Т а б л и ц а 2
|
Рост |
Число мальчиков |
а |
аP |
|
115–116 |
2 |
-3 |
-6 |
|
117–118 |
7 |
-2 |
-14 |
|
119–120 |
21 |
-1 |
-21 |
|
121–122 |
33 |
0 |
0 |
|
123–124 |
21 |
1 |
21 |
|
125–126 |
12 |
2 |
24 |
|
127–128 |
3 |
3 |
9 |
|
129–130 |
1 |
4 |
4 |
n=100
В качестве Мо
принимаем 122, т.к. из 100 наблюдений у 33 человек рост был 122см. Находим
условные отклонения (a) от условной средней в соответствии с вышесказанным.
Затем получаем произведение условных отклонений на частоты (aP) и суммируем
полученные величины (). В итоге получится 17. Наконец,
данные подставляем в формулу:
Задачи по статистике с решением — Средние величины
Решаем проверочные задачи по статистике
Тема: «Средние величины»
1. Задача на определение средней арифметической
Рассчитать средний возраст студентов в группе из 20 человек:


|
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
|
1 2 3 4 5 |
18 18 19 20 19 |
6 7 8 9 10 |
20 19 19 19 20 |
11 12 13 14 15 |
22 19 19 20 20 |
16 17 18 19 20 |
21 19 19 19 19 |
Если сгруппировать данные, то получим ряд распределения:


2. Задача на нахождение средней арифметической взвешенной
Распределение рабочих по выработке деталей
|
Выработка деталей за смену одним рабочим, шт., Хi |
18 |
19 |
20 |
21 |
22 |
Всего |
|
Число рабочих, fi |
2 |
11 |
5 |
1 |
1 |
20 |


3. Задача на вычисление средней по групповым средним или по частным средним.
Распределение рабочих по среднему стажу работы
|
Номер цеха |
Средний стаж работы, лет. |
Число рабочих, чел., fi |
|
1-й 2-й 3-й |
5 7 10 |
90 60 50 |
|
ИТОГО: |
200 |


4. Задача на вычисление средних в рядах распределения (интервальный ряд).
Распределение рабочих АО по уровню ежемесячной оплаты труда
|
Группы рабочих по оплате труда у.е. |
Число рабочих, чел. |
Середина интервала, хi |
|
До 500 |
5 |
450 |
|
500-600 |
15 |
550 |
|
600-700 |
20 |
650 |
|
700-800 |
30 |
750 |
|
800-900 |
16 |
850 |
|
900 и более |
14 |
950 |
|
Итого: |
100 |
— |

Задача 5. Вычисление средних в интервальных рядах методом моментов
Распределение малых предприятий региона по стоимости основных производственных фондов
|
Группы предприятий по стоимости ОПФ, у.е. |
Число предприятий |
Середина интервалов, х |
|
Хi*f |
|
14-16 16-18 18-20 20-22 22-24 |
2 6 10 4 3 |
15 17 19 21 22 |
-2 -1 0 1 2 |
-4 -6 0 4 6 |
|
Итого: |
25 |
— |
— |
0 |
Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот.
Один из вариантов, обладающий наибольшей частотой принимают за А, i— величина интервала.
А- начало отсчета «способ отсчета от условного нуля», «способ моментов». Все варианты уменьшим на А, затем разделим на I, получим новый вариационный ряд распределения новых вариантов хi. Средняя арифметическая их новых вариантов- момент первого порядка m i= 

Задача 6 на определение Средней гармонической.
Заработная плата предприятий АО
|
Предприятие |
Численность промышленно- производственного персонала, чел |
Месячный фонд заработной платы, тыс руб. |
Средняя заработная плата, руб. |
|
А |
1 |
2 |
3 |
|
1 2 3 |
540 275 458 |
564,84 332,75 517,54 |
1046 1210 1130 |
|
ИТОГО: |
1 273 |
1415,13 |
? |
Определить среднюю з/п по всем предприятиям.
Решение:
Составим логическую формулу средней: средняя з/п по всем предприятиям =
1) Пусть мы располагаем данными гр.1 и 2. Нам известен числитель и знаменатель логической формулы.
Искомая средняя величина определяется по средней агрегатной:

2) Пусть мы располагаем данными гр.1 и 3 , нам известен числитель логической формулы, а знаменатель числитель не известен, но может быть найден путем умножения средней з/п на численность ППП. Искомая средняя определяется по средней арифметической взвешенной.


3) Пусть мы располагаем данными гр.2 и 3 , нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления фонда з/п на среднюю з/п логической формулы. Искомая средняя определяется по средней гармонической взвешенной:
Все ответы верны.
Задача 7. Определить среднюю цену моркови по всем магазинам.
Цена и выручка от реализации по трем коммерческим магазинам.
|
№ магазина |
Цена моркови., руб за кг. |
Выручка от реализации, руб. |
|
1 2 3 |
17 20 24 |
3060 2800 1920 |
|
Итого: |
— |
7780 |
Решение.
Логическая формула средней: средняя цена моркови =
нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления выручки от реализации на цену моркови.
Искомая средняя определяется по средней гармонической взвешенной:
Задача 8 по статистике с решением: средние величины.
Информация о вкладах в банке
|
Вид вклада |
Октябрь |
Ноябрь |
||
|
Число вкладов, тыс., f |
Средний размер вклада, руб., x |
Сумма вкладов, млн. руб., F |
Средний размер вклада, x |
|
|
До востребования Срочный |
10 8 |
350 400 |
4,07 3,87 |
370 430 |
Определить средний размер вклада по двум видам.
1) Пусть в октябре известен средний размер вкладов каждого вида и число вкладов. По формуле средней арифметической взвешенной:


2) Пусть в ноябре известен средний размер вкладов каждого вида и сумма вкладов. По формуле средней гармонической взвешенной:
Задача 9: Удельная материалоемкость по двум предприятиям, изготавливающим один и тот же вид продукции составила соответственно 2,5 и 3 кг. Вычислить среднюю удельную материалоемкость изделия по двум предприятиям при условии, что каждым предприятием израсходовано на изготовления одного изделия по 60 тонн стали.
1) Решение задачи по средней арифметической простой:


2) решение по средней арифметической взвешенной



Оба решения не имеют логического смысла, чтобы правильно выбрать формулу средней величины необходимо составить логическую формулу задачи, отражающую ее смысл.
Логическая формула: средняя удельная материалоемкость по двум предприятиям = общему расходу материала на двух предприятиях/ на количество произведенных изделий→ средняя гармоническая взвешенная
3)
приравнивает моменты теоретического распределения к моментам эмпирического распределения (распределения, построенного по наблюдениям). Из полученных уравнений находятся оценки параметров распределения. Например, для распределения с двумя параметрами первые два момента (среднее и дисперсия распределения, соответственно, m и s) будут приравнены первым двум эмпирическим (выборочным) моментам (среднему и дисперсии выборки, соответственно), и затем будет произведено оценивание.
Где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала,
Назначение сервиса
. С помощью онлайн-калькулятора вычисляется среднее значение по способу моментов. Результат решения оформляется в формате Word
.
Инструкция
. Для получения решения необходимо заполнить исходные данные и выбрать параметры отчета для оформления в Word.
Алгоритм нахождения средней по способу моментов
Пример
. Затраты рабочего времени на однородную технологическую операцию распределялись между рабочими следующим образом:
Требуется определить среднюю величину затрат рабочего времени и среднеквадратическое отклонение по способу моментов; коэффициент вариации; моду и медиану.
Таблица для расчета показателей.
| Группы | Середина интервала, x i | Кол-во, f i | x i ·f i | Накопленная частота, S | (x-x ) 2 ·f |
| 5 — 10 | 7.5 | 20 | 150 | 20 | 4600.56 |
| 15 — 20 | 17.5 | 25 | 437.5 | 45 | 667.36 |
| 20 — 25 | 22.5 | 50 | 1125 | 95 | 1.39 |
| 25 — 30 | 27.5 | 30 | 825 | 125 | 700.83 |
| 30 — 35 | 32.5 | 15 | 487.5 | 140 | 1450.42 |
| 35 — 40 | 37.5 | 10 | 375 | 150 | 2200.28 |
| 150 | 3400 | 9620.83 |
Мода
где x 0 – начало модального интервала; h – величина интервала; f 2 –частота, соответствующая модальному интервалу; f 1 – предмодальная частота; f 3 – послемодальная частота.
Выбираем в качестве начала интервала 20, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 22.78 мин.
Медиана
Медианным является интервал 20 — 25, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Таким образом, 50% единиц совокупности будут меньше по величине 23 мин.
.
Находим А = 22.5, шаг интервала h = 5.
Средний квадрат отклонений по способу моментов
.
| x ц | x * i | x * i f i | 2 f i |
| 7.5 | -3 | -60 | 180 |
| 17.5 | -1 | -25 | 25 |
| 22.5 | 0 | 0 | 0 |
| 27.5 | 1 | 30 | 30 |
| 32.5 | 2 | 30 | 60 |
| 37.5 | 3 | 30 | 90 |
| 5 | 385 |
мин.
Среднее квадратическое отклонение
.
мин.
Коэффициент вариации
— мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Поскольку v>30% ,но v<70%, то вариация умеренная.
Пример
Для оценки ряда распределения найдем следующие показатели:
Средняя взвешенная
Среднее значение изучаемого признака по способу моментов
.
где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала.
Различают три вида средних величин: мода (М0), медиана (Ме), средняя арифметическая (М).
Они не могут подменить друг друга и лишь в совокупности достаточно полно и в сжатой форме представляют собой особенности вариационного ряда.
Мода (Мо)
— наиболее часто встречающаяся в ряду распределения варианта. Она дает представление о центре распределения вариационного ряда. Используется:
Для определения центра распределения в открытых вариационных рядах
Для определения среднего уровня в рядах с резко асимметричным распределением
Медиана
— это серединная варианта, центральный член ранжированного ряда. Название медиана взято из геометрии, где так именуется линия, делящая сторону треугольника на две равные части.
Медиана применяется:
Для определения среднего уровня признака в числовых рядах с неравными интервалами в группах
Для определения среднего уровня признака, когда исходные данные представлены в виде качественных признаков и когда единственным способом указать некий центр тяжести совокупности является указание варианты (группы вариант), которая занимает центральное положение
При вычислении некоторых демографических показателей (средней продолжительности предстоящей жизни)
При определении наиболее рационального места расположения учреждений здравоохранения, коммунальных учреждений и т. п. (имеется в виду учет оптимальной удаленности учреждений от всех объектов обслуживания)
В настоящее время очень распространены различные опросы (маркетинговые, социологические и др.), в которых опрашиваемых просят выставить баллы изделиям, политикам и т. п. Затем из полученных оценок рассчитывают средние баллы и рассматривают их как интегральные оценки, выставленные коллективом опрошенных. При этом обычно для определения средних показателей применяют среднее арифметическое. Однако такой способ на самом деле применять нельзя. Обоснованным в этом случае является использование в качестве средних баллов медианы или моды.
Для характеристики среднего уровня признака наиболее часто используется в медицине средняя арифметическая величина (М).
Средняя арифметическая величина
— это общая количественная характеристика определенного признака изучаемых явлений, составляющих качественно однородную статистическую совокупность.
Различают среднюю арифметическую простую и взвешенную.
Средняя арифметическая простая вычисляется для не сгруппированного вариационного ряда путем суммирования всех вариант и делением этой суммы на общее количество вариант, входящих в вариационный ряд.
Вычисляется средняя арифметическая простая по формуле:
М — средняя арифметическая взвешенная,
∑Vp — сумма произведений вариант на их частоты,
n — число наблюдений.
Помимо указанного метода прямого расчета средней арифметической взвешенной, существуют другие методы, в частности, способ моментов при котором несколько упрощены арифметические расчеты.
Расчет средней арифметической способом моментов проводится по формуле:
А — условная средняя (чаще всего в качестве условной средней берется мода М0)
d — отклонение каждой варианты от условной средней (V-A)
∑dp — сумма произведений отклонений на их частоту.
Порядок вычисления представлен в таблице (за условную среднюю принимаем М0 = 76 ударам в минуту).
| частота пульса V | Р | d (V-A) | dp |
| -16 | -16 | ||
| -14 | -28 | ||
| -12 | -36 | ||
| -10 | -30 | ||
| -8 | -24 | ||
| -6 | -54 | ||
| -4 | -24 | ||
| -2 | -14 | ||
| n= 54 | | ∑dp= -200 |
где i — интервал между группами.
Порядок вычисления представлен в табл. (за условную среднюю принимаем М 0 = 73 ударам в минуту, где i = 3)
Определение средней арифметической способом моментов
n = 54 ∑dp = -13
| М = А + | ∑dp | = | 73+ | -13*3 | = 73 — 0,7=72,3 (ударов в минуту |
| n |
Таким образом, полученное значение средней арифметической величины по способу моментов идентично таковому, найденному обычным способом.
А – условная средняя (чаще других повторяющаяся в вариационном ряду)
а – условное отклонение от условной средней (ранг)
i – интервал
1-ый этап — определение середины групп;
2-ой этап – ранжирование групп: 0 присваивается группе, частота встречаемости врианты в которой – наибольшая. Т.е. в данном случае 7-11 (частота -32). Вверх от данной группы ранжирование производится прибавляя (-1). Вниз – прибавка (+1).
3-ий этап – определение условной моды (условная средняя). А –это середина модального интервала. В нашем случае модальным интервалом является 7 -11, таким образом А = 9.
4-ый этап –определение интервала. Интервал во всех группах ряда одинаков и равен 5. i = 5/
5-й этап –определение общего числа наблюдений. n = ∑p = 103.
Подставляем, полученные данные в формулу:
Задания для самостоятельной работы
Используя данные сгруппированного вариационного ряда рассчитайте среднюю арифметическую по способу моментов.
Вариант №1
Вариант №2
Вариант №3
Вариант №4
Вариант №5
Вариант №6
Вариант №7
Вариант №8
Вариант №9
Вариант №10
Вариант №11
Вариант №12
Задача №4 Определение моды и медианы в не сгруппированном вариационном ряду с нечетным количеством вариант
Сроки стационарного лечения больных детей в днях: 15, 14, 18, 17, 16, 20, 19, 16, 14, 16, 17, 12, 18, 19, 20.
Для определения моды в вариационном ряду ранжирование ряда необязательно. Однако, прежде чем определять медиану, необходимо выстроить вариационный ряд в порядке возрастания или убывания.
12, 14, 14, 15, 16, 16, 16, 17, 17, 18, 18, 19, 19, 20, 20.
Мода = 16. Т.к. вариант 16 встречается наибольшее число раз (3 раза).
В случае если вариант, имеющих наибольшую частоту встречаемости несколько, то в вариационном ряду может быть указано две и более Моды.
Медиана в ряду с нечетным количеством определяется по формуле:
8 –это порядковый номер медианы в ранжированном вариационном ряду,
т.о. Ме = 17.
Задача №5 Определение моды и медианы в не сгруппированном вариационном ряду с четным количеством вариант.
На основе данных, приведенных в задании, требуется найти моду и медиану
Сроки стационарного лечения больных детей в днях: 15, 14, 18, 17, 16, 20, 19, 16, 14, 16, 17, 12, 18, 19, 20, 11
Строим ранжированный вариационный ряд:
11, 12, 14, 14, 15, 16, 16, 16, 17, 17, 18, 18, 19, 19, 20, 20
У нас имеется два срединных числа 16 и 17. В таком случае медиана находится как среднее арифметическое между ними. Me = 16,5.
Расчеты средней арифметической могут быть громоздкими, если варианты (значения признака) и веса имеют очень большие или очень малые значения и затрудняется сам процесс подсчета. Тогда для простоты счета используется ряд свойств средней арифметической:
1) если уменьшить (увеличить) все варианты на какое-либо произвольное число А
, то новая средняя уменьшится (увеличится) на то же число А
, т. е. изменится на ±А
;
2) если уменьшить все варианты (значения признака) в одинаковое число раз (К
), то средняя уменьшится во столько же раз, а при увеличении в (К
) раз – увеличится в (К
) раз;
3) если уменьшить или увеличить веса (частоты) всех вариант на какое-либо постоянное число А
, то средняя арифметическая не изменится;
4) сумма отклонений всех вариант от общей средней равна нулю.
Перечисленные свойства средней арифметической позволяют в случае необходимости упрощать расчеты путем замены абсолютных частот относительными, уменьшать варианты (значения признака) на какое-либо число А
, сокращать их в К
раз и рассчитывать среднюю арифметическую из уменьшенных вариант, а затем переходить к средней первоначального ряда.
Способ исчисления средней арифметической с использованием ее свойств известен в статистике как «способ условного нуля»
, или «условной средней»
, или как «способ моментов».
Кратко этот способ можно записать в виде формулы
Если уменьшенные варианты (значения признака ), обозначить через , то приведенную выше формулу можно переписать в виде .
При использовании формулы для упрощения исчисления средней арифметической взвешенной интервального ряда при определении величины какого-либо числа А
используют такие приемы его определения.
Величина А
равна величине:
1) первого значения средней величины интервала (продолжим на примере задачи, где млн дол., а .
Расчет средней из уменьшенных вариант
| Интервалы | Среднее значение интервала | Число заводов, f |
Произведение | |
| До 2 | 1,5 | 0 (1,5–1,5) | ||
| 2–3 | 2,5 | 1 (2,5–1,5) | ||
| 3–4 | 3,5 | 2 (3,5–1,5) | ||
| 4–5 | 4,5 | 3 (4,5–1,5) | ||
| 5–6 | 5,5 | 4 (5,5–1,5) | ||
| Свыше 6 | 6,5 | 5 (6,5–1,5) | ||
| Итого: | 3,7 | – | |
,
2) величину А
берем равной величине среднего значения интервала с наибольшей частотой повторений, в данном случае А
= 3,5 при (f
= 30), или значение серединной варианты, или наибольшей варианты (в данном случае наибольшее значение признака Х
= 6,5) и деленное на размер интервала (в данном примере 1).
Расчет средней при А
= 3,5, f
= 30, К
= 1 на том же примере.
Расчет средней способом моментов
| Интервалы | Среднее значение интервала | Число заводов, f |
Произведение | |
| До 2 | 1,5 | (1,5 – 3,5) : 1 = –2 | –20 | |
| 2–3 | 2,5 | (2,5 – 3,5) : 1 = –1 | –20 | |
| 3–4 | 3,5 | (3,5 – 3,5) : 1 = 0 | ||
| 4–5 | 4,5 | (4,5 – 3,5) : 1 = 1 | ||
| 5–6 | 5,5 | (5,5 – 3,5) : 1 = 2 | ||
| Свыше 6 | 6,5 | (6,5 – 3,5) : 1 = 3 | ||
| Итого: | 3,7 | – |
; ; ;
Способ моментов, условного нуля или условной средней заключается в том, что при сокращенном способе расчета средней арифметической мы выбираем такой момент, чтобы в новом ряду одной из значений признака , т. е. приравниваем и отсюда выбираем величину А
и К
.
Надо иметь в виду, что если (Х
– А
) : К
, где К
– равная величина интервала, то полученные новые варианты образуют в равноинтервальном ряду ряды натуральных чисел (1, 2, 3 и т. д.) положительных вниз и отрицательных вверх от нуля. Среднюю арифметическую из этих новых вариант называют моментом первого порядка и выражают формулой
.
Чтобы определить величину средней арифметической, нужно величину момента первого порядка умножить на величину того интервала (К
), на который делим все варианты, и прибавить к полученному произведению величину варианты (А
), которую вычитали.
;
Таким образом, способом моментов или условного нуля рассчитать среднюю арифметическую из вариационного ряда, если ряд равноинтервальный, значительно легче.
Мода
Мода – есть величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности.
Для дискретных рядов распределения модой будет значение варианты с наибольшей частотой.
Пример.
При определении плана по производству мужских туфлей фабрикой было произведено изучение покупательского спроса по результатам продажи. Распределение проданной обуви характеризовалось следующими показателями:
Наибольшим спросом пользовалась обувь 41 размера и составила 30% от проданного количества. В этом ряду распределения М
0 = 41.
Для интервальных рядов распределения с равными интервалами мода определяется по формуле
.
Прежде всего, необходимо найти интервал, в котором находится мода, т. е. модальный интервал.
В вариационном ряду с равными интервалами модальный интервал
определяется по наибольшей частоте, в рядах с неравными интервалами – по наибольшей плотности распределения, где: – величина нижней границы интервала, содержащего моду; – частота модального интервала; – частота интервала, предшествующего модальному, т. е. предмодального; – частота интервала, следующего за модальным, т. е. послемодального.
Пример расчета моды в интервальном ряду
Дана группировка предприятий по численности промышленно-производственного персонала. Найти моду. В нашей задаче наибольшее число предприятий (30) имеет группировка с численностью работающих от 400 до 500 человек. Следовательно, этот интервал является модальным интервалом ряда распространения с равными интервалами. Введем следующие обозначения:
Подставим эти значения в формулу вычисления моды и произведем расчет:
Таким образом, мы определили значение модальной величины признака, заключенного в этом интервале (400–500), т. е. М
0 = 467 чел.
Во многих случаях при характеристике совокупности в качестве обобщающего показателя отдается предпочтение моде
, а не средней арифметической. Так, при изучении цен на рынке фиксируется и изучается в динамике не средняя цена на определенную продукцию, а модальная. При изучении спроса населения на определенный размер обуви или одежды представляет интерес определение модального номера, а не средний размер, который вообще не имеет значения. Если средняя арифметическая близка по значению к моде, значит она типична.
ЗАДАЧИ ДЛЯ РЕШЕНИЯ
Задача 1
На сортосеменной станции при определении качества семян пшеницы было получено следующее определение семян по проценту всхожести:
Определить моду.
Задача 2
При регистрации цен в часы наиболее оживленной торговли у отдельных продавцов были зарегистрированы следующие цены фактической продажи (дол. за кг):
Картофель: 0,2; 0,12; 0,12; 0,15; 0,2; 0,2; 0,2; 0,15; 0,15; 0,15; 0,15; 0,12; 0,12; 0,12; 0,15.
Говядина: 2; 2,5; 2; 2; 1,8; 1,8; 2; 2,2; 2,5; 2; 2; 2; 2; 3; 3; 2,2; 2; 2; 2; 2.
Какие цены на картофель и говядину являются модальными?
Задача 3
Имеются данные о заработной плате 16 слесарей цеха. Найти модальную величину заработной платы.
В долларах: 118; 120; 124; 126; 130; 130; 130; 130; 132; 135; 138; 140; 140; 140; 142; 142.
Расчет медианы
Медианой в статистике называется варианта, расположенная в середине вариационного ряда. Если дискретный ряд распределения имеет нечетное число членов ряда, то медианой будет варианта, находящаяся в середине ранжированного ряда, т. е. к сумме частот прибавить 1 и все разделить на 2 – результат и даст порядковый номер медианы.
Если в вариационном ряду четное число вариант, тогда медианой будет половина суммы двух серединных вариант.
Для нахождения медианы в интервальном вариационном ряду определяем сначала медианный интервал по накопленным частотам. Таким интервалом будет такой, кумулятивная (накопленная) частота которого равна или превышает половину суммы частот. Накопленные частоты образуются путем постепенного суммирования частот, начиная от интервала с наименьшим значением признака.
Расчет медианы в интервальном вариационном ряду
| Интервалы | Частоты (f ) |
Кумулятивные (накопленные) частоты |
| 60–70 | 10 (10) | |
| 70–80 | 40 (10+30) | |
| 80–90 | 90 (40+50) | |
| 90–100 | 15 (90+60) | |
| 100–110 | 295 (150+145) | |
| 110–120 | 405 (295+110) | |
| 120–130 | 485 (405+80) | |
| 130–140 | 500 (485+15) | |
| Сумма: | ∑f = 500 |
Половина суммы накопленных частот в примере равна 250 (500: 2). Следовательно, медианным интервалом будет интервал со значением признака 100–110.
До этого интервала сумма накопленных частот составила 150. Следовательно, чтобы получить значение медианы, необходимо прибавить еще 100 единиц (250 – 150). При определении значения медианы предполагается, что значение признака в границах интервала распределяется равномерно. Следовательно, если 145 единиц, находящихся в этом интервале, распределить равномерно в интервале, равно 10, то 100 единицам будет соответствовать величина:
10: 145 ´ 100 = 6,9.
Прибавив полученную величину к минимальной границе медианного интервала, получим искомое значение медианы:
Или медиану в вариационном интервальном ряду можно исчислить по формуле:

где – величина нижней границы медианного интервала (); – величина медианного интервала ( =10); – сумма частот ряда (численность ряда 500); – сумма накопленных частот в интервале, предшествующем медианному ( = 150); – частота медианного интервала ( = 145).
4. Четные и нечетные.
В чётных вариационных рядах сумма частот или общее
число наблюдений выражено чётным числом, в нечётных ― нечётным.
5.
Симметричные и асимметричные.
В
симметричном вариационном ряду все виды средних величин совпадают или очень
близки (мода, медиана, среднее арифметическое).
В
зависимости от характера изучаемых явлений, от конкретных задач и целей
статистического исследования, а также от содержания исходного материала, в
санитарной статистике применяются следующие виды средних величин:
· структурные
средние (мода, медиана);
·
средняя арифметическая;
·
средняя гармоническая;
·
средняя геометрическая;
·
средняя прогрессивная.
Мода (М о)
— величина
варьирующего признака, которая более часто встречается в изучаемой совокупности
т.е. варианта, соответствующая наибольшей частоте. Находят ее непосредственно
по структуре вариационного ряда, не прибегая к каким-либо вычислениям. Она
обычно является величиной очень близкой к средней арифметической и весьма удобна
в практической деятельности.
Медиана (М е)
—
делящая вариационный ряд (ранжированный, т.е. значения вариант располагаются в
порядке возрастания или убывания) на две равные половины. Медиана вычисляется
при помощи так называемого нечетного ряда, который получают путем
последовательного суммирования частот. Если сумма частот соответствует четному
числу, тогда за медиану условно принимают
среднюю арифметическую из двух средних значений.
Мода и медиана применяются в случае незамкнутой
совокупности, т.е. когда наибольшая или наименьшая варианты не имеют точной
количественной характеристики (например, до 15 лет, 50 и старше и т.п.). В этом
случае среднюю арифметическую (параметрические характеристики) рассчитать
нельзя.
Средня
я арифметическая
—
самая распространенная величина. Средняя арифметическая обозначается чаще через
М
.
Различают
среднюю арифметическую простую и взвешенную.
Средняя арифметическая простая
вычисляется:
― в тех случаях, когда совокупность представлена
простым перечнем знаний признака у каждой единицы;
― если число повторений каждой
варианты нет возможности определить;
― если числа повторений каждой варианты близки между
собой.
Средняя
арифметическая простая исчисляется по формуле:
где V — индивидуальные значения признака; n —
число индивидуальных значений; — знак суммирования.
Таким образом, простая средняя представляет собой
отношение суммы вариант к числу наблюдений.
Пример:
определить среднюю длительность пребывания на
койке 10 больных пневмонией:
16 дней — 1 больной; 17–1; 18–1;
19–1; 20–1; 21–1; 22–1; 23–1; 26–1; 31–1.
койко-дня.
Средняя арифметическая взвешенная
исчисляется
в тех случаях, когда индивидуальные значения признака повторяются. Ее можно
вычислять двояким способом:
1. Непосредственным (среднеарифметическим или прямым
способом) по формуле:
где P — частота (число случаев) наблюдений каждой варианты.
Таким образом, средняя арифметическая взвешенная
представляет собой отношение суммы
произведений вариант на частоты к числу наблюдений.
2. С помощью вычисления отклонений от условной средней (по способу моментов).
Основой для вычисления взвешенной средней
арифметической является:
― сгруппированный материал по
вариантам количественного признака;
―
все варианты должны располагаться в порядке возрастания или убывания величины
признака (ранжированный ряд).
Для вычисления по способу моментов обязательным
условием является одинаковый размер всех интервалов.
По способу
моментов средняя арифметическая вычисляется по формуле:

где М о — условная средняя, за которую чаще
принимают величину признака, соответствующую
наибольшей частоте, т.е. которая чаще повторяется (Мода).
i — величина интервала.
a — условное отклонение от условий средней,
представляющее собой последовательный ряд чисел (1, 2 и т.д.) со знаком + для
вариант больших условной средней и со знаком–(–1, –2 и т.д.) для вариант,
которые ниже условной средней. Условное же отклонение от варианты, принятой за
условную среднюю равно 0.
P — частоты.
Общее
число наблюдений или n.
Пример:
определить средний рост
мальчиков 8 лет непосредственным способом (таблица1).
Т а б л и ц а 1
|
Рост в см |
мальчиков P |
Центральная варианта V |
|
Центральная варианта ― середина интервала ― определяется
как полу сумма начальных значений двух соседних групп:
;
и т.д.
Произведение VP получают путем умножения центральных
вариант на частоты ; и
т.д. Затем полученные произведения складывают и получают , которую делят на число наблюдений
(100) и получают среднюю арифметическую взвешенную.
см.
Эту же задачу решим по способу моментов, для чего
составляется следующая таблица 2:
Т а б л и ц а 2
|
Рост |
мальчиков |
||
В качестве М о
принимаем 122, т.к. из 100 наблюдений у 33 человек рост был 122см. Находим
условные отклонения (a) от условной средней в соответствии с вышесказанным.
Затем получаем произведение условных отклонений на частоты (aP) и суммируем
полученные величины (). В итоге получится 17. Наконец,
данные подставляем в формулу.