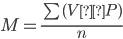Как найти средний рост учащихся - Avtoru.top - решение различных проблем

Как найти средний рост учеников

Мне кажется, что здесь нужно просто сообразить, что этот средний рост всех учеников заключен между числами $$147frac<3><7> raquo; /> и <img decoding async$ учеников без учёта роста самого маленького 147 целых и 3/7 сантиметра.
Средний рост $n-1$ учеников (т.е. не учитывается «лямка», как единица счёта, но учитывается его рост) — 148 целых и 4/7 сантиметра.
А это ничего не дает.
Даже при n=3 (при n=2 задача тривиальна) всегда можно подобрать три различных числа числа, так что:
1) Среднее двух наименьших равно $$147frac<3><7> raquo; /><br />2) Среднее двух наибольших равно <img decoding async$

Одно из предположений — опечатка в условии, и правильная формулировка:
$L_0$ , рост самого высокого $x$ , а самого низкого $y$ ,
то можно составить соотношение:
$$dfrac <x-y><8>=dfrac <n-1><7> raquo; /><br />из которого следует, как справедливо отмечал venco ,<br />что <img decoding async$ ),
а также, что разница в росте $x-y$ кратна $8$ .

Тогда можно составить другие соотношения:

Батороев
Если я нигде не напутал, то средний рост учеников (в зависимости от ) принадлежит отрезку $$left[frac<1032k+149><7k+1>;frac<1040k+147><7k+1>right] raquo; />, т.е. (объединяя отрезки) <img decoding async$ и $y$ такие, что будут удовлетворять условию, но давать разные ответы.
Например, $k=1$
$n=8$

$x=152$ , $y=144$

Написать программу на языке прлграммирования Pascal.
В компьютер вводятся по очереди данные о росте N учащихся класса. Определить средний рост учащихся класса.

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Выберите правильный вариант выражения, составьте с ним предложение.

Две новые столовые / две новых столовых; две ученические тетради / две ученических тетради; добрые три часа / добрых три часа; каждые два часа / каждых два часа; три большие дома / три больших дома; три лисьи шапки / три лисьих шапки; целые четыре месяца / целых четыре месяца; четыре высокие горы /четыре высоких горы.

Выберите правильную форму глагольного или именного управления.

Вершить судьбами – вершить судьбы; выйти с трамвая – выйти из трамвая; ехать на трамвае – ехать трамваем – ехать в трамвае; ждать поезд – ждать поезда; игнорировать на ухаживание – игнорировать ухаживание; контроль над производством – контроль за производством; любительница печения пирогов – любительница печь пироги; наблюдать за больным – наблюдать больного; не купить спички – не купить спичек; описывается о жизни – описывается жизнь; оплачивать за проезд – оплачивать проезд; отзыв о дипломной работе – отзыв на дипломную работу; памятник Пушкину – памятник Пушкина; подчеркнуть о необходимости – подчеркнуть необходимость; по окончании работ – по окончанию работ; превосходство над другими – превосходство перед другими; предел терпения – предел терпению; преимущество перед соперником – преимущество над соперником; прийти из армии – прийти с армии; продавать за три рубля – продавать по три рубля; разведка на нефть – разведка нефти; способен на жертвы – способен к жертвам; тосковать по другу – тосковать о друге; уверенность в победу – уверенность в победе; удостоен наградой – удостоен награды; характерен демократу – характерен для демократа; характеристика ученика – характеристика на ученика.

Здравствуйте! Помогите пожалуйста решить задачу по теме Паскаль : В группе определить самого высокого мальчика и самую маленькую девочку.

1. Определить средний рост девочек и мальчиков одного класса. Количество учеников в классе заранее неизвестно.

Uses crt;
Var
b,g: Array[1..100] of Integer;
d,m,s1,s2,i: Integer;
sr1,sr2: Real;
BEGIN
Clrscr;
Writeln(‘Количество мальчиков: ‘); Readln(m);
Writeln(‘ВВОД:’);
For i:=1 to m do
begin
Readln(b[i]);
s1:=s1+b[i];
end;
sr1:=s1/m;
Writeln(‘Количество девочек: ‘); Readln(d);
Writeln(‘ВВОД:’);
For i:=1 to d do
begin
Readln(g[i]);
s2:=s2+g[i];
end;
sr2:=s2/d;
Writeln(‘Ср. рост мальчиков: ‘,sr1:2:2);
Writeln(‘Ср. рост девочек: ‘,sr2:2:2);
Readln
END.

2. В ЭВМ вводятся по очереди данные о росте N учащихся класса. Определить средний рост учащихся класса.

Var m:integer; i,n:byte; s:real;
begin
s:=0;
Writeln(‘Vveddite kol-o uchenikov’);
readln(n);
for i:=1 to n do
begin
readln(m);
Writeln(i ,’ chlen = ‘,m);
s:=s+m;
end;
Writeln(‘srednee ‘,s/n:1:1);
readln;
end.

3. По данным свединием об участниках класса определить среднюю массу мальчиков и средний рост девочек.Кто из участников класса самый высокий?

TYPE student=record
fam,pol:string;
rost:100..220;
mas:30..200;
end;
var
s:array[1..100] of student;
i,n,u:integer; sr,sv,kd,km,max:real;
begin
write(‘Количество учеников= ‘);
readln(n);
writeln(‘Введите данные об учениках’);
for i:=1 to n do
begin
writeln(i,’ ученик’);
with s[i] do
begin
write(‘Фамилия: ‘); readln(fam);
write(‘Пол (М/Ж): ‘); readln(pol);
write(‘Рост: ‘); readln(rost);
write(‘Вес: ‘); readln(mas);
end;
end;

for i:=1 to n do
begin
with s[i] do
begin
if pol=’М’ then
begin
km:=km+1;
sv:=sv+mas;
end;
if pol=’Ж’ then
begin
kd:=kd+1;
sr:=sr+rost;
end;
end;
end;

sv:=sv/km;
sr:=sr/kd;
writeln(‘Средняя масса мальчиков= ‘,sv);
writeln(‘Средний рост девочек= ‘,sr);

max:=100;
for i:=1 to n do
begin
with s[i] do
if rost>max then
begin
max:=rost;
u:=i;
end;
end;
with s[u] do
writeln(‘Самый высокий = ‘,fam);

4. Рост 20 учеников класса представлен в виде массива. Рост мальчиков условно задан отрицательными числами. Определить средний рост мальчиков и средний рост девочек.

Program fff;
Const
n = 20;
type
mas = array[1..n] of real;
var
M,D,m1,d1: integer;
a: mas;
i: byte;
begin
randomize;
for i:=1 to n do a[i] := Random(450)-300;
for i:=1 to n do
if a[i] > 0 then
begin
D := D + Trunc(a[i]);
d1 := d1 + 1;
end
else
begin
M := M + Trunc(a[i]);
m1 := m1 + 1;
end;
writeln (‘Средний рост девушек:= ‘, D/d1:0:2);
writeln (‘Средний рост мальчиков:= ‘, M/m1*-1:0:2);
end.

На основе данных примеров, если хоть немного разбираетесь в паскале без труда решите свою задачку. Удачи!

Как найти средний рост учеников

Задача без использования массивов. Определите средний рост учащихся всего класса.
С клавиатуры вводится натуральное N. За ним последовательно вводятся данные о росте N учащихся.

Вводятся по очереди данные о росте N учащихся класса, Определить средний рост учащихся в классе
Составить программу согласно заданию. Задание: В ЭВМ вводятся по очереди данные о росте N.

Источник

Записать в файлследующие данные об учениках : фамилия , имя , отчество , рост , масса .
Вычислить , каков средний рост учеников , рост самого высокого и самого низкого учеников .
Дописать эту информацию в файл

Светило науки — 45 ответов — 0 раз оказано помощи

а в чем вопрос? как найти средний рост? чтобы найти средний рост надо сложить все значения (например, три ученика. у одного рост 150 см, у второго 161 см, а у третьего 152 см. 150 см+161 см+152 см=463 см), а потом разделить на их количество (ученика было три, поэтому делим на 3. 463 см/3=154,3 см). таким образом мы находим средний рост всех учеников.

Источник

В таблице хранятся следующие данные об учениках: фамилия, имя, отчество, рост, вес. Вычислить средний рост учеников, найти самого

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Научный форум dxdy

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву , правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

О среднем росте учеников в классе (олимпиада 6-8 класс)

Последний раз редактировалось PAV 17.06.2011, 15:33, всего редактировалось 1 раз.

Измерялся рост учеников в классе. Измерялся с точностью до одного сантиметра. Без учета роста самого низкого ученика средний рост всех остальных учеников в этом классе составил 147 целых и 3/7 сантиметра. А без учета самого рослого ученика, он составил 148 целых и 4/7 сантиметра. Сказанно, что число учеников в классе не превышает 40. Найти средний рост всех учеников этого класса.

Это олимпиадная задача нашего города. Адрессована к ученикам 6-8-ого класса. Я уже давно не ученик. Олимпиада тоже давно прошла. А задача эта так же давно не дает покоя. Трудность в том, что если допустить опечатку, повлекшую отстутствие какого либо данного, то не могу предположить какого именно данного. При подключении любого дополнительного данного решение становится слишком очевидным. А между тем задача — олимпиадная.
Помогите избавиться от назойливой задачи.

Мне кажется, что здесь нужно просто сообразить, что этот средний рост всех учеников заключен между числами $$147frac<3><7>$» /> и <img decoding=$ учеников в классе. Средний рост $n$ учеников без учёта роста самого маленького 147 целых и 3/7 сантиметра.
Средний рост $n-1$ учеников (т.е. не учитывается «лямка», как единица счёта, но учитывается его рост) — 148 целых и 4/7 сантиметра.
А это ничего не дает.
Даже при n=3 (при n=2 задача тривиальна) всегда можно подобрать три различных числа числа, так что:
1) Среднее двух наименьших равно $$147frac<3><7>$» /><br />2) Среднее двух наибольших равно <img decoding=$ .

Для начала хотелось бы понять условие.
Допустим, ученики упорядочены по росту:

Одно из предположений — опечатка в условии, и правильная формулировка:
$'. dfrac <sumlimits_<i=2>^ <n>a_i> <n-1>= 148</p> <p>4/7$» /><br /><img decoding=$ , общий рост учеников $L_0$ , рост самого высокого $x$ , а самого низкого $y$ ,
то можно составить соотношение:
$$dfrac <x-y><8>=dfrac <n-1><7>$» /><br />из которого следует, как справедливо отмечал venco ,<br />что <img decoding=$ (где ),
а также, что разница в росте $x-y$ кратна $8$ .

Тогда можно составить другие соотношения:

Не берусь утверждать, но есть подозрение , что на основе анализа степеней четности членов, входящих в эти выражения,
решение все же можно найти.

Батороев
Если я нигде не напутал, то средний рост учеников (в зависимости от ) принадлежит отрезку $$left[frac<1032k+149><7k+1>;frac<1040k+147><7k+1>right]$» />, т.е. (объединяя отрезки) <img decoding=$ можно подобрать разные значения $x$ и $y$ такие, что будут удовлетворять условию, но давать разные ответы.
Например, $k=1$
$n=8$

$x=152$ , $y=144$

$$dfrac <1184><8>=148$» /></p> <p><img decoding=$ , $y=145$

$$dfrac <1185><8>=148,125$» /></p> <h2>Описательная статистика</h2> <p>На прошлом занятии мы уже начали работать с данными и статистикой. Сегодня мы продолжим этот путь.</p> <h4>Какая бывает статистика</h4> <p><img decoding=$

Иногда данных бывает так много, что чтобы увидеть картину в целом, их нужно обобщить. Этим занимается описательная статистика (Descriptive Statistics).

Причем обобщить правильно, чтобы наши измерения отражали реальное положение вещей. Известное высказывание Марка Твена о том, что «существует три вида лжи: ложь, наглая ложь и статистика», верно лишь в той степени, в которой мы сознательно или по незнанию искажаем сбор и описание данных. Сама статистика здесь ни при чем.

Кроме того, довольно часто нам нужно составить представление о явлении, охватить которое наблюдением мы не можем. Например, мы хотим понять насколько эффективно новое лекарство, но обследовать всех, кто его принял, не представляется возможным. Статистический вывод (Statistical Inference) позволяет сделать обоснованное предположение о явлении в целом по ограниченному числу наблюдений.

На этом занятии мы поговорим про описательную статистику, на следующем — займемся статистическим выводом.

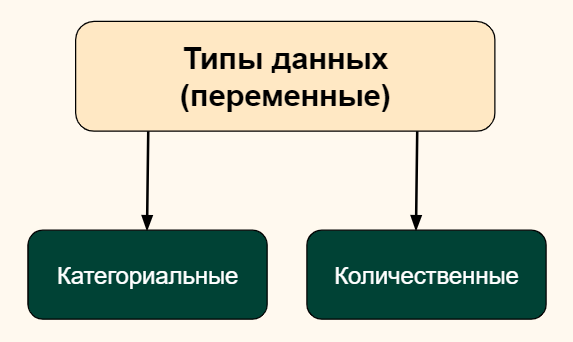
Начнем с того, что данные (или как еще говорят переменные) бывают двух видов, категориальные и количественные.

1. Категориальные (качественные) данные

Это данные, которые можно отнести к какой-то категории (categorical data). Например, людей можно разделить на мужчин и женщин, на детей и взрослых. Категориями могут быть профессии, группа крови, принадлежность к политической партии. Разделение книг по жанрам или потребителей по степени их удовлетворенности будет категориальной переменной.

Пример: сколько студентов учится на каждом курсе университета

Единицей наших данных в этом примере будут студенты. Категорией будет курс.

Самое простое, что мы можем сделать при работе с такой переменной, это взять наблюдения каждой категории и посчитать их количество. График, который помогает оценить такие данные, называется столбчатой диаграммой (bar chart).

Мы уже знакомы с библиотекой Matplotlib. Ей и воспользуемся.

Какой вывод можно сделать на основе этих данных? До пятого курса доходят не все. Причем больше всего студентов отчисляется после второго курса, руководству вуза стоит обратить внимание именно на этих студентов. Без графика картина была бы не так очевидна.

Теперь про количественные данные.

2. Количественные данные

Примером количественных данных (quantitative data) может быть рост и вес людей, расстояние до объекта, уровень дохода и цена товара. Количественные данные — это всегда какое-то числовое значение, не категория.

Пример: рост мужчин в России

Давайте будем спрашивать у мужчин на улице, какой у них рост и поместим эти данные в питоновский список:

Теперь для удобства создадим группы или интервалы (bin) роста и посчитаем, сколько людей попадет в каждый из этих интервалов. В этом нам поможет функция hist из той же библиотеки Matplotlib.

Источник

Рост девочек в см, V	Центральная варианта группы, V₁	Число девочек, P	V₁ · P
133,0 – 136,9		3	135 ´3 = 405
137,0 – 140,9		15	139 ´ 15 = 2085
141,0 – 144,9		17	143 ´ 17 = 2431
145,0 – 148,9		41	147 ´ 41 = 6027
149,0 – 152,9		52	151 ´ 52 = 7852
153,0 – 156,9		42	155 ´ 42 = 6510
157,0 – 160,9		18	159 ´ 18 = 2862
161,0 – 164,9		5	163 ´ 5 = 815
165,0 – 168,9		4	167 ´ 4 = 668
		n = 197	å V ₁P = 29655

см

Величина
того или иного признака неодинакова у
всех единиц наблюдения совокупности,
несмотря на ее относительную однородность.
Например, уровень АД у отдельных лиц,
страдающих артериальной гипертензией,
неодинаков. В этом проявляется разнообразие
(колеблемость) признака в изучаемой
совокупности. Средняя арифметическая
величина находится в большой зависимости
от колеблемости вариационного ряда.
Чем меньше колеблемость ряда (разность
между самой большой и самой малой
величиной), тем более точно его будет
характеризовать средняя арифметическая.

Если
большинство вариант концентрируется
около своей средней арифметической
величины, то такой вариационный ряд –
довольно однородный. Если же варианта
значительно удалена от своей средней
арифметической – налицо большое
варьирование, а возможно, и неоднородная
совокупность.

Критериями,
наиболее полно определяющими уровень
разнообразия каждого признака в
совокупности, являются: среднее
квадратическое отклонение (d)
и коэффициент вариации (C_V).

Для
вычисления среднего
квадратического отклонения
(d)
необходимо
определить отклонения (d)
каждой варианты от средней, возвести
их в квадрат (d²),
перемножить квадрат отклонений на
частоту каждой варианты (d²p),
получить сумму этих произведений (å
d²p),
а затем вычислить d
по формуле:

При
малом числе наблюдений (n£30)
расчет производится по формуле:

Значение среднего
квадратического отклонения – d:

d
характеризует однородность вариационного
ряда. Если d
мала, значит ряд однородный и рассчитанная
М достаточно верно характеризует данный
вариационный ряд. Если d
велика, то ряд неоднородный и полученная
М характеризует не весь ряд, а какую-то
ее часть.
В медицине, ЗДО
интервал М ±
1d
обычно принимают за пределы нормы.
Теоретическое
распределение вариант в однородном
ряду подчиняется правилу
трех сигм:

М
±
1d
= 68,3%

М
±
2d
= 95,5%

М
±
3d
= 99,7%.

В
пределах М±1d
находится 68,3% всех вариант (наблюдений),
в пределах М±2d
– 95,5%, а в пределах М±3d
– 99,7% вариант, составляющих совокупность.
Если 95,5% всех вариант находится в пределах
М±2d,
то средняя арифметическая является
характерной для данного ряда и не
требуется увеличивать число наблюдений
в совокупности. Для определения типичности
средней арифметической сравнивают
фактическое распределение с теоретическим
путем расчета сигмальных отклонений.

Для
оценки варьирования признака в
совокупности наряду со средним
квадратическим отклонением может быть
использован коэффициент
вариации
(C_V).
Особенно необходимо использовать
коэффициент вариации для сравнения
варьирования двух или более средних
величин, выраженных в разных единицах
измерения (сантиметрах, килограммах и
др.):

Значение коэффициента
вариации менее
10% свидетельствует
о малой колеблемости, от
10 до 20% – о
средней, больше
20% – о сильной
колеблемости вариант вокруг средней.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Пример выполненной лабораторной работы № 3

«Изучение изменчивости. Построение вариационного ряда и кривой».

Цель: познакомиться с закономерностями модификационной изменчивости, выработать умения строить вариационный ряд и график изменчивости изучаемого признака; вычислять среднюю величину признака, определять норму реакции

Оборудование: ростомер, рулетка, карандаш, линейка

Ход работы:

Измерьте рост каждого школьника в классе с точностью до сантиметра, округлив цифры.
Расположите данные в порядке нарастания величины признака, получите вариационный ряд и запишите данные вариационного ряда в таблицу.

Каждое конкретное значение изучаемого признака называют вариантой V

Таблица № 1

№

Vвариант
(рост
см)

Сгруппируйте полученные цифры, которые отличаются друг от друга на 5 см. (например, 150-155 см, 156-160 см, 161-165 см. ).

Подсчитайте количество учеников входящих в каждую группу и заполните таблицу.

Частота встречаемости отдельных вариант обозначается буквой P

Таблица № 2

V варианта рост (см) 150 -155 156 -160 161 -165 166 -170 171 -175 176 — 180 181 -186

Р частота встречаемости
(количество учащихся)

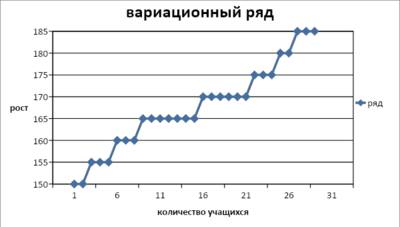
5. Постройте вариационный ряд.

С этой целью:

— по оси абсцисс отложите на одинаковом расстоянии количество учащихся;

— по оси ординат отложите числовые значения признака (рост)

Пример:

6. Постройте вариационную кривую

На основании вариационного ряда строится вариационная кривая — графическое отображение частоты встречаемости каждой варианты.

С этой целью:
— по оси абсцисс отложите на одинаковом расстоянии отдельные варианты роста в нарастающем порядке;
— по оси ординат отложите числовые значения, соответствующие частоте повторяемости каждой варианты

Пример:

7. Вычислите среднюю величину признака (средний рост учеников).

Среднее значение признака встречается чаще, а вариации, значительно отличающиеся от него, — значительно реже. Это называется нормальным распределением.

M – среднее значение признака

V – значение варианты

P – частота встречаемости варианты

n – общее число вариант вариационного ряда

8. Определите норму реакции и широту нормы реакции.

Норма реакции ________

Определите широту нормы реакции для этого из максимального значения признака вычислите минимальное.

max-min= __________

Выводы:

1. Длина вариационного ряда свидетельствует о …………………………………………………………………………………………………

2. Графическим выражением модификационной изменчивости признака является……………………………………………………………………

3. Пределы вариационной изменчивости признака ограничены……………………………………………………………………………………………..

Источник

V варианта рост (см)	150 -155	156 -160	161 -165	166 -170	171 -175	176 — 180	181 -186
Р частота встречаемости (количество учащихся)

Как найти средний рост учеников

Написать программу на языке прлграммирования Pascal. В компьютер вводятся по очереди данные о росте N учащихся класса. Определить средний рост учащихся класса.

Здравствуйте! Помогите пожалуйста решить задачу по теме Паскаль : В группе определить самого высокого мальчика и самую маленькую девочку.

Как найти средний рост учеников

В таблице хранятся следующие данные об учениках: фамилия, имя, отчество, рост, вес. Вычислить средний рост учеников, найти самого

Научный форум dxdy

О среднем росте учеников в классе (олимпиада 6-8 класс)

1. Категориальные (качественные) данные

Пример: сколько студентов учится на каждом курсе университета

2. Количественные данные

Пример: рост мужчин в России

Не пропустите также:

Написать программу на языке прлграммирования Pascal.
В компьютер вводятся по очереди данные о росте N учащихся класса. Определить средний рост учащихся класса.