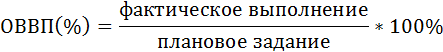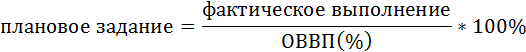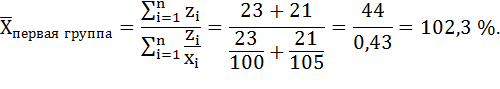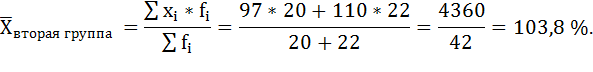Основные выводы:
-
Формула для расчета среднего процента — [(процент 1 + процент 2) (объем выборки 1 + объем выборки 2)] x 100
-
Используйте средний процент при определении среднего значения двух или более процентов от целого.
Расчет среднего процента от чего-либо может показаться простой задачей, но эта концепция может быть сложнее, чем может показаться на первый взгляд. Хотя в некоторых случаях вы можете просто усреднить два процента, сложив их и разделив на количество используемых процентов, в других случаях вам может потребоваться учесть такие факторы, как размер выборки.
В этой статье мы обсудим проценты и способы вычисления среднего процента, а также приведем примеры использования формулы среднего процента в различных сценариях.
Понимание процентных соотношений
В базовом смысле проценты — это соотношение или доля чего-либо от 100. Например, если у вас есть коробка со 100 шоколадными конфетами и 35 из них наполнены ванильным кремом, это означает, что 35% шоколадных конфет имеют вкус ванильного крема. Проценты используются в различных аспектах повседневной жизни, в том числе в школе и на предприятиях. Расчет среднего процентного показателя также может быть использован в ряде различных сценариев. Например, инвестор может захотеть определить, как два разных запаса изменяются со временем по отношению друг к другу. Чтобы понять эту взаимосвязь, инвестору необходимо знать, как рассчитать среднее значение двух процентов запасов.
Как рассчитать среднее значение
Прежде чем мы сможем объяснить, как рассчитать средний процент, мы должны сначала определить, как рассчитать среднее значение. Среднее значение набора чисел — это просто сумма чисел, деленная на общее количество значений в наборе. Например, чтобы найти среднее значение 12, 15, 24, 78, 3, 313 и 10, просто сложите эти числа (12 + 15 + 24 + 78 + 3 + 313 + 10 = 455) и разделите на общее количество значений в наборе (7), чтобы получить среднее значение 65.
Как рассчитать средний процент
Вычисление среднего значения двух или более процентов требует иного набора шагов, чем определение среднего значения двух или более обычных чисел. При вычислении среднего процента необходимо учитывать несколько моментов, включая тот факт, что часто сначала необходимо вычислить реальные числа, которые представляет процент.
Для расчета среднего процента в большинстве случаев используйте следующие шаги:
1. Преобразуйте проценты, которые вы хотите усреднить, в десятичные числа
Первый шаг в вычислении среднего процентного показателя — перевести проценты в десятичные числа. Допустим, вы хотите определить среднее значение 30% от 150 и 25% от 200. Преобразуйте эти два процента в десятичные числа, разделив их оба на 100. Это означает, что 30% — это 0.3 как десятичная дробь и 25% — это .25 как десятичная дробь.
2. Определите число, которое представляет каждая десятичная дробь
После того, как вы перевели проценты в десятичные дроби, вам нужно найти число, которое представляет каждая десятичная дробь. Для этого нужно умножить десятичную дробь на общее количество в выборке. Таким образом, используя предыдущий пример, вы умножите 0.3 на 150, чтобы получить 45 и умножить .25 на 200, чтобы получить 50.
3. Сложите числа вместе
Следующим шагом будет сложение двух чисел, найденных на предыдущем этапе. Таким образом, 45 плюс 50 равно 95.
4. Сложите объемы выборки
Также необходимо сложить объемы выборки для каждого процента. Таким образом, 150 плюс 200 равно 350.
5. Рассчитайте среднее процентное значение
Чтобы найти средний процент из двух процентов в этом примере, нужно сначала разделить сумму двух процентных чисел на сумму двух объемов выборки. Итак, 95 разделить на 350 равно 0.27. Затем вы умножаете десятичную дробь на 100, чтобы получить средний процент. Итак, 0.27 умножить на 100 равно 27 или 27%. Это означает, что средний процент 30% от 150 и 25% от 200 составляет 27%.
Формула среднего процента
Ниже приведена формула, которая может быть использована для расчета большинства средних процентных показателей:
[(Процент 1 + процент 2)(объем выборки 1 + объем выборки 2)] x 100 = средний процент
В этой формуле процент 1 представляет собой десятичное значение данного процента от объема выборки 1. Чтобы определить значение процента 1, вы должны сначала преобразовать процент в десятичную дробь, а затем умножить десятичную дробь на размер выборки. Повторите этот шаг, чтобы определить десятичное значение процента 2 в этой формуле. После того как вы рассчитали десятичные значения каждого процента для каждого данного размера выборки, вы складываете эти десятичные значения вместе и делите полученное число на общую сумму обоих размеров выборки. Затем нужно умножить это значение на 100, чтобы получить средний процент.
Пример расчета средних процентов
Ниже приведен пример расчета среднего процента в реальных условиях:
Компания XYZ хочет определить средний процент того, сколько продуктов было продано из двух различных категорий продуктов в данном году. В первой категории товаров компания произвела 500 товаров и продала 75% из них. Во второй категории компания произвела 400 продуктов и продала 60% из них.
Для определения среднего процента проданных товаров из обеих категорий выполняются следующие действия:
-
Переведите оба процента в десятичные дроби. Итак, 75 разделить на 100 равно .75 и 60 разделить на 100 равно .60. Это дает вам .75 и .60 как представление двух процентов проданных продуктов из обеих категорий товаров.
-
Умножьте десятичные значения на общее количество продукции, произведенной в каждой категории. Итак,, .75 умножить на 500 равно 375 и .60 умножить на 400 равно 240. Это означает, что 75% от 500 составляет 375, а 60% от 400 равно 240.
-
Сложите два числа, которые представляют процентное соотношение товаров из каждой категории. Итак, 375 плюс 240 равно 615.
-
Сложите вместе общее количество продукции, произведенной в каждой категории. Так, 500 плюс 400 равно 900.
-
Разделите сумму процентов на сумму общего количества продуктов, произведенных в каждой категории. Так, 615, разделенное на 900, равно 0.68.
-
Умножьте десятичную дробь на 100, чтобы получить средний процент. Таким образом, 0.68 умножить на 100 равно 68, или 68%.
Используя эту формулу, компания XYZ продала в среднем 68% продуктов из двух категорий товаров, которые были проанализированы.
При составлении различных статистических отчётов нередко возникает необходимость расчёта среднего процента выполнения плана. Это может быть, например, план по выпуску продукции или план по оказанию каких-либо услуг.
Подразумевается, что имеется несколько статистических единиц (например, фабрика или отдельный вид продукции), у которых есть различная норма выработки.
Как рассчитать средний процент выполнения плана
Для того, чтобы найти средний процент выполнения плана по выпуску продукции, можно воспользоваться несколькими формулами:
1) Средняя гармоническая взвешенная.
2) Средняя арифметическая взвешенная.
Если в задаче неизвестна плановая величина, а просто указан процент выполнения плана, то применяется 1 формула.
Если план для каждого показателя известен, то применяется 2 формула.
Примеры расчёта среднего процента
1) Имеется 3 цеха, выпускающие одинаковую продукцию. Известен фактический выпуск продукции и процент выполнения плана по каждому цеху.
1 цех — 200 млн. рублей, выполнение плана — 105%.
2 цех — 250 млн. рублей, выполнение плана — 110%.
3 цех — 180 млн. рублей, выполнение плана — 90%.
Нужно посчитать средний процент выполнения плана.
Так как плановая величина не задана, то используем формулу средней гармонической взвешенной.
Средний процент будет равен 1,02*100% = 102%.
Таким образом, план по 3 цехам перевыполнен на 2 процента.
2) Даны 2 вида продукции.
Для первого вида годовой план изготовления — 700 единиц. План был выполнен на 105%.
Для первого вида годовой план изготовления — 1000 единиц. План был выполнен на 90%.
Нужно найти средний процент выполнения плана.
Так как известны плановые показатели для каждого из видов продукции, используем формулу средней арифметической взвешенной.
Средний процент получился равным 99,11%.
Таким образом, план недовыполнен на 0,89 процентов.
Как вычислить средний процент
Средней величиной в статистике называется обобщающий показатель, который дает характеристику уровня изменений однородных единиц совокупности. В любом случае между характеризуемыми признаками обязательно должна присутствовать взаимосвязь.

Инструкция
Определите, по какой средней величине вы будете характеризовать единицы совокупности. Это может быть средняя арифметическая, средняя геометрическая, средняя геометрическая и средняя кубическая. Выбор зависит от исходных данных для расчета и взаимосвязи между ними. Проще всего вычислить показатель по средней арифметической величине. Для расчета используется формула: Хар=Оз/Ос, где Оз — общая объем значения признака, Ос — общий объем совокупности. Допустим, вам необходимо вычислить средний процент просроченной задолженности за год по филиалам предприятия.
Выберите количественные показатели изменения признака за анализируемый период. Для данного примера сложите сумму просроченной задолженности на конец года по каждому филиалу (Оз). Определите общий объем совокупности, то есть найдите сумму общей задолженности по всем филиалам на конец года (Ос). Рассчитайте средний процент просроченной задолженности по средней арифметической, подставив значения числителя и знаменателя в формулу и умножив полученное число на 100%. Полученное число будет являться средним процентом просроченной задолженности по всем филиалам этого предприятия.
К некоторым средним величинам в статистике относится расчет среднего процента брака на производстве. Этот показатель вычисляется по формуле: Бс=Бп/Оп*100%, где Бп-стоимость бракованной продукции, Оп-общий объем произведенной продукции в стоимостном выражении.
Определите стоимость бракованной продукции и общую стоимость произведенной продукции за анализируемый период по данным бухгалтерского учета. Стоимость брака отражается на счете 28 «Брак в производстве». Стоимость общего объема производства можно вычислить, сложив данные по строке 020 «Себестоимость произведенной и реализованной продукции» отчета о прибылях и убытках и данные бухгалтерского баланса о стоимости остатков готовой продукции и незавершенного производства. Вычислите средний процент брака, подставив найденные значения числителя и знаменателя в указанную формулу.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
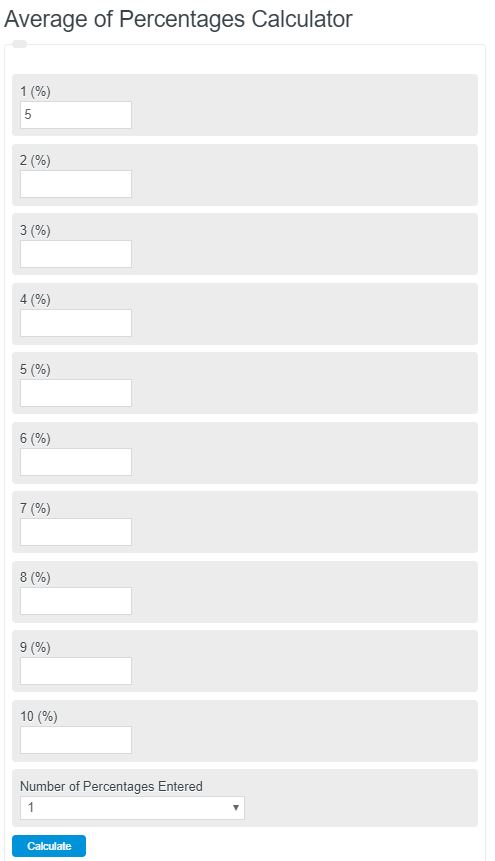
Enter the average of up to 10 different percentages into the calculator. The calculator will return the average percentage of those values.
- Average Rating Calculator
- Fraction to Percent Calculator
- Fraction to decimal calculator
The following formula is used to calculate the average of a group of percentages.
AV % = X1 + X2 + X… / #
- Where AV % is the average percent
- X1..etc are the percentages of each value
- # is the total number of values
Average of Percentages Definition
The average of percentages is the true average of a set of two or more percentage values.
Average of Percentages Example
Example Problem #1:
First, gather all of the percentages together. For this example, the percentages are 10%, 25%, 12%, and 3%.
Next, sum all of the percentages together. Adding the values from above together yields:
= 10 + 25 + 12 + 3 = 50%.
Next, determine the total number of percentages. For this example, there were 4 percentages added together.
Finally, calculate the average of the percentages using the formula above:
AV % = X1 + X2 + X… / #
AV % = 50%/ 4
AV % = 12.5%
FAQ
What is a percentage?
A percentage is a ratio of a number to a total of 100%. For example, 1 out of 10 would be 10%.
How to calculate the average of percentages
- First, sum all of the percentages together
Add all of the percentages together to get one value. For example, if you had 1%, 2%, and 3%, the sum would be 6%.
- Next, count the number of values
This is the total number of values. In the example above, this number would be 3, since there are 3 separate percentages.
- Calculate the average
Enter the information into the equation above to determine the average.
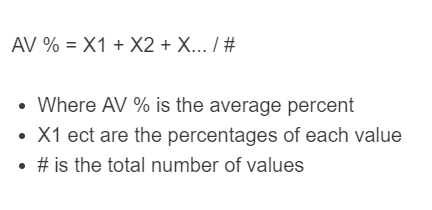
Расчет среднего процента
Средний процент — это среднее значение процента по результатам трех значений.
Формула расчета среднего процента:
Пср = (П1 + П2 + П3) / 3
Пср — средний процент
П1 — первое измерение
П2 — второе измерение
П3 — третье измерение
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета среднего процента (по результатам трех значений) и формула для расчета среднего процента. С помощью этого калькулятора вы в один клик сможете вычислить средний процент.
Как посчитать средний процент
9. Как вычислять средний процент?
Рассмотрим несколько более сложную задачу.
Найти средний процент выпуска I сорта за год.
Определяя количество тонн изделий I сорта по каждому кварталу, предварительно находим, что всего за год выпущено том числе I сорта:
что составляет 78,7% всего выпуска.
Если взять просто среднее число процентов выпуска I сорта по кварталам, то получим ( что заметно больше правильного ответа.
Как посчитать средний показатель в процентах
Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.
Смысл коэффициента
Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:
Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.
Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.
Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.
Помогите посчитать средний процент. Нужна формула
Доставка Товара 1 стоимостью 25000 р. обойдется в 59% от стоимости
Доставка Товара 2 стоимостью 4000 р. обойдется в 30% от стоимости
Сколько процентов в среднем обойдется доставка обоих Товаров.
Стоимость доставки Товара 1 равна 25 000 * 0,59 = 14 750 (руб.) ;
доставка Товара 2: 4000 * 0,3 = 1200 (руб.) .
Суммарная стоимость товаров равна 25 000 + 4000 = 29 000 (руб.) ;
суммарная стоимость доставки: 14 750 + 1200 = 15 950 (руб. )
В процентном отношении стоимость доставки обоих товаров составит
На основании данных о выполнении плана двумя группами заводов вычислите средний процент выполнения плана выпуска продукции для каждой группы.
| Первая группа | Вторая группа | ||||
|---|---|---|---|---|---|
| № завода | фактический выпуск продукции млн.д.е. | выполнение плана выпуска продукции % | № завода | плановое задание выпуска продукции, млн. д.е. | выполнение плана выпуска продукции % |
| 1 | 23 | 100 | 3 | 20 | 97 |
| 2 | 21 | 105 | 4 | 22 | 110 |
Решение:
Относительная величина выполнения плана определяется по формуле:
Величина планового задания будет тогда равна отношению фактического выпуска к показателю выполнения плана по выпуску продукции.
Вычислим средний процент выполнения плана выпуска продукции для первой группы.
Для этого воспользуемся формулой средней агрегатной, где в числителе будет суммарный показатель стоимости фактического выпуска продукции, а в знаменателе суммарное значение стоимости планируемого выпуска продукции рассчитанного по предыдущей формуле для каждого завода отдельно:
Средний процент выполнения плана выпуска продукции для первой группы составил 102,3%.
Для вычисления среднего процента выполнения плана выпуска продукции для второй группы воспользуемся формулой средней арифметической взвешенной.
Средний процент выполнения плана выпуска продукции для второй группы составил 103,8%.
Условие задачи взято из практикума: Общая теория статистики: практикум / С.А. Клещёва. – Пинск: ПолеcГУ, 2009. – 114 с
Автор решения: Роман Гриб