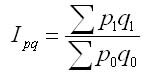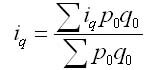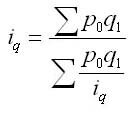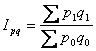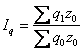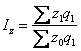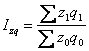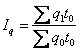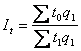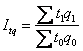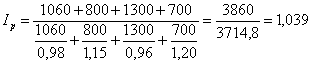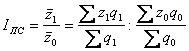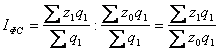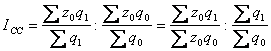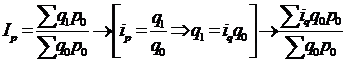Средние индексы
В
статистической практике получили
распространение средние
индексы. Они
рассчитываются в двух формах — средней
арифметической и средней гармонической.
-
Рассмотрим
агрегатный индекс физического объёма
продукции:
Jq
=
.
Из
формулы индивидуального индекса выразим
q1=
iq
* q0.
Отсюда:
Jq
=
—
это среднеарифметический индекс
физического объёма продукции.
Задача
Данные
о реализации мебели в магазине:
|
Товары |
Товарооборот, |
Изменение |
iq |
|
|
Май |
Июнь |
|||
|
Диваны |
200 |
250 |
+7 |
(100+7)/100=1,07 |
|
Столы |
140 |
170 |
-11 |
(100-11)/100=0,89 |
|
Стулья |
60 |
40 |
+23 |
(100+23)/100=1,23 |
|
ИТОГО |
400 |
460 |
— |
— |
|
Усл. |
q0p0 |
q1p1 |
— |
— |
Вычислить:
-
индекс
товарооборота; -
средний
индекс физического объёма продаж
мебели; -
индекс
цен.
Индекс товарооборота:
Jpq
=
=
= 1,150 (товарооборот возрос на 15,0 %).
Средний
индекс физического объёма продаж мебели:
Jq
=
=
= 1,031 (физический объём возрос на 3,1 %).
Индекс
цен (находим через взаимосвязь индексов):
Jp
=
=
= 1,115 (цены на мебель в среднем возросли
на 11,5 %).
-
Рассмотрим
агрегатный индекс цен:
Jp
=
.
Из
формулы индивидуального индекса выразим
p0
= p1
/ ip
.
Отсюда:
Jp
=

Задача
По
одному из магазинов города имеются
данные:
|
Товары |
Товарооборот, тыс. |
Изменение |
ip |
|
|
Август |
Сентябрь |
|||
|
Ткани |
230 |
232 |
+8,5 |
(100+8,5)/100=1,085 |
|
Ковры |
195 |
190 |
+0,9 |
(100+0,9)/100=1,009 |
|
Швейная фурнитура |
76 |
61 |
-3,1 |
(100-3,1)/100=0,969 |
|
ИТОГО |
501 |
483 |
— |
— |
|
Усл. |
q0p0 |
q1p1 |
— |
— |
Вычислить:
-
индекс
товарооборота; -
средний
индекс цен; -
индекс
физического объёма продаж.
Рассчитать
индекс цен, абсолютный перерасход
(экономию) покупателей от общего повышения
(снижения) цен в магазине.
Индекс товарооборота:
Jpq
=
=
= 0,964 (товарооборот снизился на 3,6 %).
Средний
индекс цен:
Jp
=

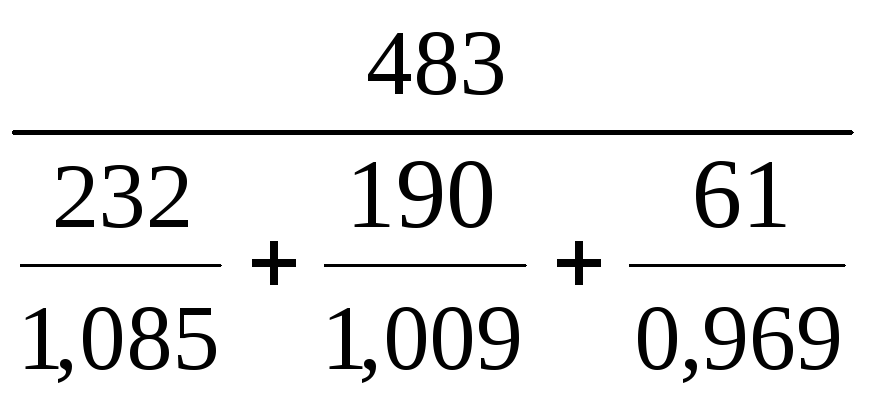
= 1,039 (цены в среднем возросли на 3,9 %).
Так
как цены возросли, покупатели понесли
дополнительные расходы, то есть за те
же товары они фактически заплатили
дороже. Сумма перерасхода покупателей
от общего повышения цен на овощи
составила: 483 — 465 = 18 тыс. руб. Соответственно,
в случае снижения цен покупатели экономят
определённую сумму денег. Расчёт суммы
экономии осуществляется тем же способом:
числитель минус знаменатель индекса
цен.
Индекс
физического объёма продаж (находим
через взаимосвязь индексов):
Jq
=

= 0,928 (физический объём продаж снизился
на 7,2 %).
По
среднегармонической формуле можно
рассчитать и другие индексы качественных
показателей:
-
индекс
урожайности:
Ju
=
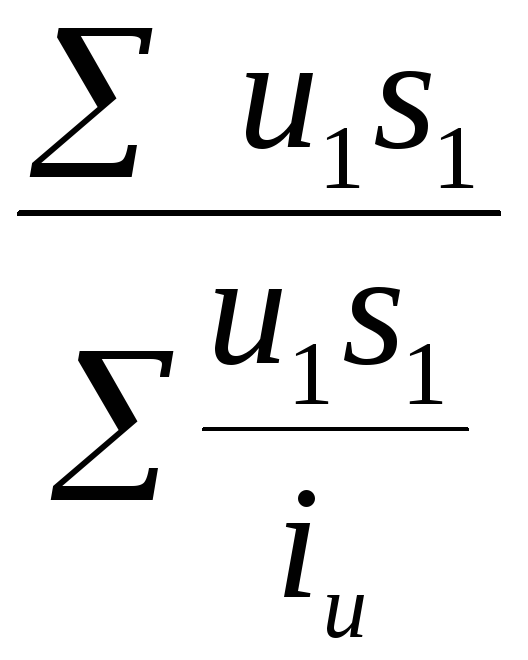
-
индекс
себестоимости:
Jz
=

-
индекс
заработной платы:
JL
=

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Индексный
метод — один из самых распространенных методов статистического анализа
экономических явлений. С помощью индексов изучаются народное хозяйство в целом
и его отдельные отрасли, а также деятельность предприятий, объединений, фирм,
хозяйств и др.; выявляется динамика развития социально-экономических явлений,
анализируется выполнение планов или норм; определяется влияние отдельных
факторов на общий результат, вскрываются резервы производства; проводятся
территориальные и международные сопоставления экономических показателей.
Индексом
в статистике называется относительный показатель, характеризующий соотношение
во времени, по сравнению с планом или в пространстве уровней социально-экономических
явлений. Так как индекс — относительный показатель, то он всегда получается при
соотношении двух величии: отчетной (или текущей), т. е. сравниваемой, и
базисной, т. е. той, с уровнем которой сравнивается отчетная величина. Если за
базу сравнения берется уровень явления за какой-то прошлый период времени,
получают динамические индексы; если за базу сравнения берется уровень явления
на другой территории, получают территориальные индексы, а если за базу
сравнения берется какой-либо нормативный уровень, получают индексы выполнения
плана, индексы выполнения норм и т. д.
В
формулах, системах уравнений, экономико-математических моделях текущие данные
помечаются единицей, стоящей чуть ниже буквенного обозначения величины.
Как
и всякая относительная величина, индексы выражаются в виде коэффициентов, если
за основание принимается единица, или в виде процентов, если за основание
принимается сто.
Социально-экономические
явления, изучаемые статистикой, обычно состоят из многих элементов. Так,
валовой выпуск продуктов и услуг включает стоимость конечных товаров и услуг,
созданных всеми общественно организованными видами экономической деятельности и
во всех отраслях экономики. Другими словами, валовой выпуск продуктов и услуг
состоит из многих отдельных видов продуктов и услуг.
Индексы
рассчитываются как для отдельных элементов сложного явления, так и для всего
сложного явления в целом. В первом случае они называются индивидуальными и
обозначаются латинской буквой
, а во второй —
общими и обозначаются
. К индивидуальным
индексам относятся индексы, характеризующие изменение выпуска одного
какого-либо вида продукции (индексы выплавки стали, добычи калийных удобрений,
производства телевизоров и др.), индексы, характеризующие изменение цены
какого-либо товара (велосипедов, цемента, говядины и др.), себестоимости
отдельного изделия и т.д.
К
индексам, исчисленным для всего сложного явления, то есть к общим, относятся
индексы, характеризующие динамику выпуска всей продукции предприятия, отрасли и
др., динамику цен группы товаров, или всех товаров, или набора
продовольственных и непродовольственных товаров и услуг, входящих в «потребительскую
корзинку», динамику себестоимости ряда изделий и т. д.
Общие
индексы используются для сопоставления непосредственно несоизмеримых,
разнородных явлений. Например, с помощью общих индексов можно охарактеризовать
динамику выпуска продукции всей промышленности или динамику объемов всей
выпускаемой продукции на мебельной фабрике, изготавливающей различные виды
продукции: столы, кресла, диваны, шкафы. Однако нельзя просто сложить объемы
продукции различных видов за два периода и отнести эти суммы одну к другой.
Такое суммирование бессмысленно не только из-за различных единиц измерения
(тонны, штуки, метры и др.), но также из-за того, что каждый вид продукции
имеет свое назначение и произведен с разными затратами средств и общественно
необходимого времени.
Чтобы
сделать сопоставимыми несоизмеримые явления (или их элементы), нужно выразить
их общей мерой; стоимостью, трудовыми затратами и т. д. Эта задача решается
построением и расчетом общих индексов. Основной формой общих индексов являются
агрегатные индексы.
Агрегатный
индекс состоит из двух элементов: индексируемых величин, изменение которых
должен отразить индекс, и показателей, которые служат соизмерителями (весами).
Произведение
каждой индексируемой величины на соизмеритель (вес) должно давать определенную
экономическую категорию.
Значение
индексируемой величины всегда изменяется: отчетное значение сопоставляется с
базисным. Конкретное название индекса дается всегда по индексируемой величине.
Например, если индексируется цена, то получают индекс цен, если индексируется физический объем,
получают индекс физического объема и т. д.
Показатель-соизмеритель
(вес) выполняет функцию веса по отношению к индексируемой величине. Значение
соизмерителя (веса) в конкретном индексе принимается одинаковым в числителе и
знаменателе, чтобы исключить влияние соизмерителя на изменение индексируемого
показателя. Веса индексов могут быть выражены в стоимостных, трудовых и других
единицах измерения, а также в виде относительных величин структуры. При
построении агрегатных индексов важно правильно выбрать веса индексов. Они
должны выбираться с учетом сущности исследуемого социально-экономического
явления, чтобы сохранить экономический смысл индекса и получить возможность на
его основе исчислять абсолютные суммы экономического эффекта.
В
зависимости от содержания и характера индексируемой величины различают индексы
количественных (объемных) показателей и индексы качественных показателей.
Количественные (экстенсивные) показатели характеризуют общий, суммарный размер
того или иного явления, например, количество (физический объем) продукции в
натуральном выражении, численность работников, общие затраты времени на
произведенную продукцию, размер посевной площади и т. д. Качественные
(интенсивные) показатели характеризуют размер признака в расчете на единицу
совокупности: цена единицы продукции (товара), себестоимость единицы продукции,
затраты рабочего времени па единицу продукции (трудоемкость единицы продукции),
выработка продукции на одного работающего, расход материала (топлива) на
единицу продукции, урожайность культуры в расчете на один гектар и т. п. Как
правило, качественные показатели представляют собой либо средние значения, либо
относительные величины.
Существует
правило построения агрегатных факторных индексов, в соответствии с которым в
индексах качественных показателей весами выступают показатели отчетного
периода, а в индексах количественных показателей — базисного периода.
Соответствующие
количественные (объемные) и качественные показатели тесно связаны друг с другом.
В общем виде эта взаимосвязь выражается в том, что произведение качественного
показателя на связанный с ним количественный показатель дает новый показатель,
другую экономическую категорию. Например, если перемножить цену одного изделия
(
, качественный
показатель) на количество этих изделий (
, количественный
показатель), то получим общую стоимость данных изделий или товарооборот (
, новый
показатель); произведение удельного расхода материала
на количество единиц продукции
представляет собой
общий расход материала (
, новый
показатель); произведение урожайности культуры на ее посевную площадь дает
валовой сбор этой культуры (новый показатель) и т. д. Эта взаимосвязь между
количественными и качественными показателями справедлива при построении и
исчислении их агрегатных индексов.
Например,
произведение агрегатного индекса цен
на агрегатный индекс физического объема
равно агрегатному индексу стоимости продукции
(товарооборота)
.
Агрегатный
индекс цен
определяется по формуле:
Агрегатный
индекс цен характеризует, как изменились в среднем цены на различные виды
продукции, включенные в расчет общего индекса цен.
Агрегатный
индекс физического объема
характеризует, как изменился в среднем общий
объем продукции по анализируемому перечню. Он определяется по формуле:
Индекс
стоимости продукции (товарооборота) определяется по формуле:
Индекс
стоимости продукции характеризует изменение фактической стоимости произведенной
или реализованной продукции или же размера товарооборота по анализируемой
совокупности.
Взаимосвязь
индексов может быть представлена выражением:
Используя
эти формулы, можно по двум известным индексам определить третий.
Агрегатный
индекс является основной, но не единственной формой общего индекса. Общий
индекс может быть исчислен и как средняя величина индивидуальных индексов. Эта
средняя может быть рассчитана как средняя арифметическая и как средпяя
гармоническая. Как одна, так и другая средняя выводятся из агрегатных индексов
и дают результаты, тождественные этим индексам. Выбор формы индекса зависит от
характера исходных данных. Если известны значения индексируемого показателя и
веса в отчетном (текущем) и базисном периодах, то пользуются агрегатной формой
индексов. Если отсутствуют значения индексируемого показателя или веса в
отчетном или базисном периодах, по известны изменения индексируемого показателя
или веса по отдельным единицам изучаемой совокупности, то пользуются формой
средних индексов.
При сравнении уровней
средних величин отчетного и базисного периодов получают индекс, который в
статистике называют индексом переменного состава. Так, например, индекс
себестоимости переменного состава исчисляется по формуле:
На индекс переменного
состава (динамику средних величин) оказывают влияние два фактора: во-первых,
изменение уровней осредняемого признака (в нашем
примере изменение уровней себестоимости продукции по каждому из предприятий) и,
во-вторых, изменение долей единиц совокупности с различными значениями признака
(структурные сдвиги).
Индекс переменного состава
вычисляют и по такой формуле:
где
Индекс себестоимости
постоянного фиксированного состава рассчитывают по формуле:
или
Индекс
структурных сдвигов исчисляют по формуле:
или
Взаимосвязь индексов:
Вычитая из числителя
каждого из индексов приведенной системы знаменатель, получим разложение
абсолютного изменения (прироста) среднего уровня признака за счет
непосредственного изменения уровней осредняемого
признака (индивидуальных уровней себестоимости), так и за счет изменения
удельных весов (структурных сдвигов):
Задача 1
Динамика средних цен и
объема продажи на колхозных рынках города характеризуется следующими данными:
| Продукция | Продано продукции, тыс. кг | Средняя цена за 1 кг, тыс. р. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Колхозный рынок №1 | ||||
| Картофель | 4.0 | 4.2 | 6.4 | 7.6 |
| Капуста | 2.5 | 2.4 | 7.2 | 8.4 |
| Колхозный рынок №2 | ||||
| Картофель | 10.0 | 12.0 | 7.6 | 7.0 |
На основании имеющихся данных вычислите:
- Для колхозного рынка №1 (по двум видам продукции):
- а) индивидуальные индексы цен, физического объема и стоимости;
- б) общий индекс товарооборота;
- в) общий индекс цен;
- г) общий индекс физического объема товарооборота;
- Определите в отчетном периоде абсолютный прирост товарооборота и разложите по
факторам ( за счет изменения цен и объема продаж товаров). - Покажите взаимосвязь между исчисленными индексами.
- Для колхозных рынков вместе (по картофелю):
- а) индекс цен переменного состава
- б) индекс цен постоянного состава
- в) индекс влияния изменения структуры объема продаж картофеля на динамику средней цены
- Объясните разницу между величинами индексов постоянного и переменного состава.
- Определите общее абсолютное изменение средней цены картофеля в отчетном периоде
по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней
цен и за счет изменения структуры продаж картофеля. - Сформулируйте выводы.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Вычисление индивидуальных индексов товарооборота, цен и физического объема
Вычислим индивидуальные индексы цен:
Картофель:
Капуста:
Цены на картофель увеличились на 18,8%, а на капусту на 16,7%
Вычислим индивидуальные индексы физического объема:
Картофель:
Капуста:
Физический объем продаж картофеля увеличился на 5%, а физический
объем продаж капусты снизился на 4%.
Вычислим индивидуальные индексы стоимости продаж:
Картофель:
Капуста:
Стоимость продаж картофеля увеличилась на 24,7%, а капусты на 12%.
Вычисление общих индексов товарооборота, цен и физического объема
Общий индекс товарооборота можно вычислить по формуле:
где
— цена,
-количество проданной продукции
Общий индекс цен вычисляем по формуле:
Общий индекс физического объема
товарооборота:
Эти индексы связаны между собой формулой:
Таким образом, товарооборот увеличился на 19,4%, в том числе за счет
увеличения цен на 17,9%, за счет увеличения физического объема товарооборота на
1,3%
Разложение на факторы абсолютного прироста товарооборота
Абсолютный прирост товарооборота:
В том числе за счет изменения цены:
В том числе за счет изменения продажи товаров:
Абсолютные приросты связаны между собой формулами:
Таким образом, товарооборот
увеличился на 8,48 млн.р., в том числе за счет увеличения цен на 7,92 млн.р.,
за счет увеличения физического объема товарооборота на 0,56 млн.р.
Вычисление индесов средней цены переменного состава, постоянного состава и структурных сдвигов
Вычислим для 2-х колхозных
рынков по картофелю индекс цен переменного состава:
Вычислим индекс цен постоянного состава:
Вычислим индекс влияния изменения структуры объема продаж картофеля на
динамику средней цены:
Разница между индексами
переменного и постоянного состава заключается в том, что индекс переменного
состава равен соотношению средних уровней
цены, а постоянного характеризует изменение средней
цены за счет изменения только цен на каждом рынке.
Таким образом, средняя цена на рынках уменьшилась на 1.4%. Если бы на
обоих рынках структура продаж была одна и та же, средняя цена бы уменьшилась на 1.9% Увеличение доли более дорогого рынка в
структуре продаж увеличило среднюю цену на 0,4%.
Разложение на факторы абсолютного прироста средней цены
Определим общее абсолютное изменение цены картофеля:
Общее абсолютное изменение
цены за непосредственного изменения уровней цен картофеля:
Общее абсолютное изменение цены за счет изменения структуры продажи
картофеля:
Таким образом, средняя цена на
картофель снизилась на 0,11 тыс.р., в том числе за счет непосредственного
изменения уровней цен на 0,14 тыс.р. Увеличение доли рынка с более дорогим
картофелем увеличило результативный показатель на 0,03 тыс.р.
Задача 3
Имеются
следующие данные о выпуске одноименной продукции по трем цехам предприятия:
| Цех |
Произведено продукции, тыс.шт. |
Себестоимость производства единицы продукции, руб. |
||
| базисный период | отчетный период | базисный период | отчетный период | |
| 1 | 86 | 56 | 34.0 | 39.0 |
| 2 | 152 | 146 | 52.0 | 56.0 |
| 3 | 134 | 132 | 48.0 | 46.0 |
Определите:
- Индексы себестоимости переменного состава, постоянного состава и индекс
структурных сдвигов. - Абсолютное изменение средней себестоимости производства единицы продукции в
отчетном периоде по сравнению с базисным: а) общее; б) за счет изменения
себестоимости производства единицы продукции в отдельных цехах; в) за счет
изменения структуры произведенной продукции. - Установите
и проверьте взаимосвязи: а) между рассчитанными индексами; б) между
рассчитанными абсолютными изменениями. Поясните, в чем состоит структурный
сдвиг в производстве продукции в отчетном периоде по сравнению с базисным. - Сделайте
выводы.
Решение
Индексы себестоимости постоянного и переменного состава
Вычислим индекс себестоимости
переменного состава:
Вычислим индекс себестоимости постоянного состава:
Таким образом, средняя себестоимость в отчетном периоде увеличилась на
6%, при условии одинаковой структуры производства в цехах, себестоимость
увеличилась на 3,8%.
Индекс структурных сдвигов
Вычислим индекс влияния изменения структуры производства продукции на
динамику средней себестоимости:
Разница между индексами
переменного и постоянного состава заключается в том, что индекс переменного
состава равен соотношению средних уровней
себестоимости, а постоянного
характеризует изменение средней себестоимости за счет изменения только
себестоимости в каждом цеху. Структурный сдвиг состоит в изменение доли цехов с
более высокой (более низкой) себестоимостью.
Взаимосвязь между рассчитанными индексами будет следующая:
Индексы средней себестоимости в разностной форме
Определим общее абсолютное изменение себестоимости:
Общее абсолютное изменение
себестоимости за счет
непосредственного изменения уровня
себестоимости:
Общее абсолютное изменение себестоимости за счет изменения структуры
производства продукции:
Проверка:
Вывод к задаче
Средняя себестоимость изделия в отчетном периоде увеличилась на 2,8
руб., в том числе за счет изменения уровня себестоимости на 1,8 руб.,
увеличение доли продукции с более высокой себестоимостью увеличило
результативный показатель на 1 руб.
Количественные и качественные индексы (индексы стоимости, индексы физического объема)
Индекс физического объема продукции является стандартным индексом количественных показателей. Сложность при его построении заключается в том, что объемы различных видов продукции и товаров в натуральном выражении несопоставимы и не могут суммироваться. Например, бессмысленно складывать тонны нефти с литрами кефира, килограммы колбасы и сыра. Причиной несоизмеримости есть неоднородность — различие натуральной формы и свойств.
Единство разных видов продукции или товаров заключается в том, что они являются продуктами общественного труда, имеют определенную стоимость и ее денежный измеритель — цену (р).
Каждый продукт имеет еще себестоимость (z) и трудоемкость (t). Эти качественные показатели могут быть использованы в качестве общей меры — коэффициента соизмерения разнородных продуктов. Умножив объем продукции каждого вида q на соответствующую цену р, себестоимость продукции, трудоемкость единицы продукции, получаются сравнимые показатели, которые можно суммировать.
Коэффициенты соизмерения обеспечивают количественное сравнение, позволяют учитывать вес продукта в реальном экономическом процессе. Поэтому их показатели-сомножители, связанные с индексируемыми величинами, называют весами индексов, а умножение на них — взвешиванием.
Стоимость продукции рассчитывается как произведение количества продукции в натуральном выражении q на цену единицы продукции.
Агрегатный индекс стоимости продукции
Агрегатный индекс стоимости продукции или товарооборота рассчитывается как отношение стоимости продукции текущего периода в текущих ценах к стоимости продукции базисного периода в базисных ценах
Агрегатный индекс стоимости рассчитывается по формуле:
Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции отчетного периода по отношению к базисному либо сколько процентов составляет рост или снижение стоимости продукции. Его величина зависит от двух факторов: цены и изменения количества продукции.
Для того, чтобы узнать, на сколько денежных единиц увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным, необходимо использовать формулу:
Средние арифметические и средние гармонические взвешенные индексы физического объема продукции
Для построения средневзвешенного физического объема продукции в качестве базы необходимо брать его агрегатную форму.<
Из формулы индивидуального индекса объема продукции i = q1/q0 находим. Подставив полученное уравнение в формулу, получим общий индекс физического объема в форме среднего арифметического индекса физического объема продукции, где весами является стоимость отдельных видов продукции в базисном периоде (q0p0):
Для расчета среднего гармонического взвешенного индекса физического объема продукции нужно из формулы индивидуального индекса объема продукции выразить q0 = q1/iq и подставить его в знаменатель агрегатной формы:
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 10.
Расчёт общих индексов.
Студент должен:
знать:
— область применения и методику расчёта общих индексов;
уметь:
— исчислить общие индексы
количественных и качественных показателей;
— формулировать вывод по полученным
результатам.
Методические указания
Общими индексами
называются индексы, выражающие обобщённые результаты изменения всех
единиц изучаемой сложной совокупности. Важной особенностью этих индексов
является то, что в них соединены разнородные единицы совокупности и такие индексы
позволяют изучать влияние отдельных факторов на изменение изучаемого явления.
Если индексы охватывают не все элементы сложного явления, а только их часть, то
такие индексы называются групповыми индексами, или субиндексами. Групповые индексы
отражают закономерности в развитии отдельных частей изучаемых явлений. В таких индексах проявляется их
связь с методом группировок.
В зависимости от формы построения различают общие индексы агрегатные
и средние.
Средние индексы, в свою очередь, делятся на арифметические и гармонические. Агрегатная форма общих индексов является основной
формой экономических индексов. Средние индексы – производные, они получаются в
результате преобразования агрегатных индексов.
По характеру объекта исследования общие индексы подразделяются на индексы
количественных (объёмных) показателей и индексы качественных показателей.
В основе такого деления индексов лежит
вид индексируемой величины. Например, к количественным индексам относится
индекс физического объёма продукции, а к качественным индексам – индекс цен на
продукцию.
По составу явления можно выделить две группы сложных индексов:
индексы постоянного (фиксированного)
состава и индексы переменного состава. Деление индексов на эти две группы используется для анализа
динамики средних показателей.
С помощью экономических
индексов решаются следующие задачи:
—
измерение
динамики социально – экономических явлений за два и более
периодов времени;
—
измерение
динамики среднего экономического показателя;
—
измерение
соотношения показателей по различным регионам;
—
определение
степени влияния изменений значений одних показателей
на динамику других показателей;
—
пересчёт
значения макроэкономических показателей из фактических цен в
сопоставимые.
Каждая из этих задач
решается с помощью различных индексов.В
экономических расчётах чаще всего используются общие индексы, которые
характеризуют изменение совокупности в целом. Построение этих индексов и
является содержанием индексной методологии. В индексной теории сложились две
концепции: синтетическая и аналитическая. Они по-разному
интерпретируют общие индексы.
Согласно синтетической
концепции особенность общих индексов состоит в том, что они выражают
относительное изменение сложных (разнотоварных)
явлений, отдельные части или элементы которых непосредственно несоизмеримы, и
поэтому индексы – показатели синтетические. Например, предприятие выпускает
несколько видов продукции, имеющей различное назначение и единицы измерения.
Следовательно, путём суммирования количества произведённых товаров различных
видов нельзя получить показатель физического объёма продукции, Методология
построения общих индексов предусматривает, прежде всего, приведение разнотоварных явлений
к соизмеримому виду.
В аналитической теории
индексы рассматриваются как показатели, необходимые для измерения влияния
изменения составных частей, компонентов, факторов сложного явления на изменение
уровня этого явления. Например, изменение общей величины стоимости продукции в
отчётном периоде по сравнению с базисным периодом связано как с изменением физического
объёма выпущенной продукции, так и с изменением цен по каждому виду продукции.
Поэтому индексная методология предусматривает определение влияния каждого из
факторов на изменение уровня изучаемого явления.
Таким образом, общие
индексы являются и синтетическими и аналитическими показателями.
Общие индексы строят как
для количественных, так и для качественных показателей.
В зависимости от цели
исследования и наличия исходных данных используют различную форму построения общих индексов: агрегатную или средневзвешенную.
Основной формой общих
индексов являются агрегатные индексы. Агрегатный индекс – это сложный
относительный показатель, характеризующий среднее изменение социально –
экономического явления, состоящего из несоизмеримых элементов.
Своё название агрегатные
индексы получили от латинского «aggrego», что значит «присоединяю». В
числителе и знаменателе агрегатных индексов содержатся соединённые наборы –
агрегаты элементов изучаемой совокупности. Числитель и знаменатель агрегатного
индекса представляют собой сумму произведений двух величин, одна из которых
изменяется (индексируемая величина),
а другая остаётся неизменной в числителе и знаменателе (вес индекса).
Для вычисления индекса
надо иметь не менее двух величин изучаемого явления. Основным элементом
индексного соотношения является индексируемая величина. Под индексируемой
величиной понимают признак, изменение значения которого является
объектом изучения.
В сложных совокупностях
сопоставимость разнородных единиц достигается путём введения специальных
сомножителей индексируемых величин. Эти сомножители называются весами – соизмерителями. Их роль при определении агрегатных индексов
состоит в том, чтобы обеспечить переход от натуральных измерителей разнородных
единиц совокупности к однородным единицам. При этом в числителе и знаменателе
агрегатного индекса изменяются лишь значения индексируемой величины, а их веса
– соизмерители остаются на одном уровне. Это
необходимо для того, чтобы на величине индекса сказывалось лишь влияние
изучаемого фактора. Т.о. вес индекса – это величина,
служащая для целей соизмерения индексируемых величин.
За каждым экономическим
индексом стоят определённые экономические категории. Экономическое содержание
индекса определяет методику его расчёта. Методика построения агрегатного
индекса предусматривает решение трёх вопросов:
1)
какая
величина будет индексируемой;
2)
по
какому составу разнородных элементов явления необходимо исчислить индекс;
3)
что
будет служить весом при расчёте индекса.
При выборе веса индекса
принято руководствоваться правилом: если строится индекс количественного
показателя, то веса берутся за базисный период; если строится индекс
качественного показателя, то используются веса отчётного периода.
Например, общий индекс количественного показателя – физического объёма продукции
имеет вид: 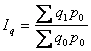
вид:
Характеристика общих индексов
|
Наименование индекса |
Формула |
Что показывает индекс |
Что показывает значение индекса, уменьшенное на 100%, т. е. [I×100-100] |
Что показывает разность знаменателя |
|
Индекс |
|
Во |
На сколько процентов изменилась стоимость продукции |
На сколько рублей изменилась стоимость продукции в результате роста |
|
Индекс цен |
|
Во сколько раз изменилась |
На сколько процентов изменилась стоимость продукции |
На сколько рублей изменилась стоимость продукции в результате роста |
|
Индекс стоимости продукции (товарооборота) |
|
Во |
На |
На |
|
Индекс |
|
Во |
На |
На сколько рублей изменились издержки производства продукции в результате роста (уменьшения) |
|
Индекс |
|
Во |
На |
На |
|
Индекс |
|
Во сколько раз возросли (уменьшились) издержки производства |
На |
На |
|
Индекс |
|
Во сколько раз изменились |
На сколько процентов изменились затраты времени |
На сколько человеко – часов увеличились (уменьшились) затраты времени на |
|
Индекс производительности труда |
|
Во сколько раз увеличилась (уменьшилась) производительность труда, или сколько процентов |
На |
Абсолютный размер экономии (перерасхода) затрат живого труда в связи с ростом (уменьшением) его производитель ности |
|
Индекс |
|
Во |
На |
На сколько человеко – часов увеличились (уменьшились) затраты |
Средняя форма общего индекса.
Агрегатная форма общих
индексов является основной формой экономических индексов, а средние индексы –
производные, они получаются в результате преобразования агрегатных индексов.
Расчёт средних общих индексов
рассмотрим на следующих примерах:
Пример 1. На основании следующих данных определить общее изменение
физического объема выпущенной
продукции:
|
Вид продукции |
Стоимость продукции базисного периода, тыс. рублей ( |
Изменение количества продаваемых товаров в отчетном |
|
А Б В |
3800 4400 2100 |
-10 +12 -22 |
Указать вид применяемого индекса. Сделать вывод.
Решение:
Общий индекс физического объёма
продукции имеет вид: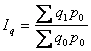
где — стоимость продукции
отчётного периода в ценах базисного периода, тыс.руб.;
— стоимость продукции
базисного периода в ценах базисного
периода, тыс.руб.
Индивидуальный индекс физического
объёма продукции имеет вид:
(2), следовательно
(3). Подставим формулу
(3) в формулу (1) и получим
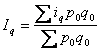
индекс физического объёма продукции
Индивидуальный индекс физического объёма продукции
составляет:
Для товара А
Для товара Б
Для товара В
Средний арифметический индекс физического объёма продукции
составляет
т.е. в результате [0,970×100-100=-3] уменьшения физического объёма выпуска
продукции в среднем на 3% , стоимость выпущенной продукции в отчётном периоде
[9986-10300=-314] уменьшилась по сравнению
с базисным периодом на 314 тыс. руб.
Пример 2. На
основании данных таблицы вычислить общее изменение
цен на продукцию в отчётном периоде по сравнению с базисным
периодом:
|
Товар |
Стоимость продукции отчетного периода в действующих ( |
Изменение цен в отчетном периоде по сравнению с базисным, % |
|
А Б В Г |
1060 800 1300 700 |
— + 15 — 4 + 20 |
Указать вид применяемого индекса. Сделать вывод
Решение:
Общий индекс цен имеет вид: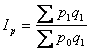
где — стоимость продукции
отчётного периода в действующих ценах, тыс.руб.;
— стоимость продукции
отчётного периода в ценах базисного периода, тыс.руб.
Индивидуальный индекс цены имеет вид:
(2),
следовательно (3).Подставим формулу (3) в формулу (1) и получим

гармонический индекс цен
Индивидуальный индекс цены продукции составляет:
Для товара А
Для товара Б
Для товара В
Для товара Г
Средний гармонический индекс цен составляет
т.е. в результате
[1,039×100-100=3,9] прироста
физического объёма выпуска продукции на 3,9% , стоимость выпущенной продукции в
отчётном периоде [3860-3714,8=145,2]
увеличилась по сравнению с базисным периодом на 145,2 тыс.руб.
Индексы структурных сдвигов.
При изучении динамики
качественных показателей приходиться определять изменение средней величины
индексируемого показателя, которое обусловлено взаимодействием двух факторов —
изменением значения индексируемого показателя у отдельных групп единиц и
изменением структуры явления. Под
изменением структуры явления понимается изменение отдельной групп единиц
совокупности в общей их численности. Так, средняя заработная плата на
предприятии может вырасти в результате роста оплаты труда работников или
увеличения доли высокооплачиваемых сотрудников. Снижение трудоёмкости
производства единицы продукции по совокупности предприятий отрасли может быть
обусловлено повышением производительности труда на предприятиях или
концентрацией производства продукции на заводах с низкой трудоёмкостью. Так как на изменение среднего значения
показателя оказывают воздействие два фактора, возникает задача определить
степень влияния каждого из факторов на общую динамику средней.
Эта задача решается с помощью индексного
метода, т.е. путём построения системы взаимосвязанных индексов, в которую
включаются три индекса: переменного состава, постоянного состава и структурных
сдвигов.
Индексом переменного состава называется индекс, выражающий соотношение
средних уровней изучаемого явления, относящихся к разным периодам времени.
Например, индекс переменного состава себестоимости продукции одного и того же
вида рассчитывается по формуле.
Где IПС— индекс переменного состава. Индекс
переменного состава отражает изменение не только индексируемой величины (в
данном случае себестоимости), но и структуры совокупности (весов)
Индекс постоянного (фиксированного) состава — это индекс, исчисленный с весами,
зафиксированными на уровне одного какого- либо периода, и показывающий
изменения только индексируемой величины. Индекс фиксированного состава
определяется как агрегатный индекс.
Так, индекс фиксированного состава себестоимости продукции рассчитывается по
формуле.
Где IФС— индекс фиксированного состава.
Под индексом структурных сдвигов понимают индекс ,
характеризующий влияния изменения структуры изучаемого явления на динамику
среднего уровня этого явления. Индекс определяется по формуле ( при изучении изменения среднего уровня себестоимости )
Где Iсс— индекс структурных сдвигов.
Система взаимосвязанных
индексов при анализе динамики средней себестоимости имеет следующий вид: , т.е. индекс переменного состава можно представить в виде
произведения индекса фиксированного состава и индекса структурных сдвигов.
Средний арифметический и средний гармонический индексы, область их применения/ Цепные и базисные индексы
Контрольная работа по дисциплине «Статистика»
I. Введение
Возрастающий
интерес к статистике вызван современным этапом развития экономики в стране,
формирования рыночных отношений. Это требует глубоких экономических знаний в
области сбора, обработки и анализа экономической информации.
Полная
и достоверная статистическая информация является тем необходимым основанием, на
котором базируется процесс управления экономикой. Вся информация, имеющая
народнохозяйственную значимость, в конечном счете, обрабатывается и
анализируется с помощью статистики.
Именно
статистические данные позволяют определить объемы валового внутреннего продукта
и национального дохода, выявить основные тенденции развития отраслей экономики,
оценить уровень инфляции, проанализировать состояние финансовых и товарных
рынков, исследовать уровень жизни населения и другие социально-экономические
явления и процессы.
Овладение
статистической методологией — одно из условий познания конъюнктуры рынка,
изучения тенденций и прогнозирования, принятия оптимальных решений на всех
уровнях деятельности.
Сложной,
трудоемкой и ответственной является заключительная, аналитическая стадия
исследования. На этой стадии рассчитываются средние показатели и показатели
распределения, анализируется структура совокупности, исследуется динамика и
взаимосвязь между изучаемыми явлениями и процессами.
На
всех стадиях исследования статистика использует различные методы. Методы
статистики — это особые приемы и способы изучения массовых общественных
явлений.
В
данной работе затрагивается тема экономических индексов. Поскольку объекты
изучения индексов весьма разнообразны, то они широко применяются в
экономической практике.
II. Теоретическая часть.
2.1. Индексы и их классификация
В
статистике под индексом понимается относительная величина (показатель),
выражающая изменение сложного социально- экономического показателя во времени,
в пространстве, по сравнению с планом. В связи с этим различают динамические,
территориальные индексы, а также индексы выполнения плана.
Многие
общественные явления состоят из непосредственно несопоставимых явлений, поэтому
основной вопрос – это вопрос сопоставимости сравниваемых явлений.
К
какому бы экономическому явлению ни относились индексы, чтобы рассчитать их,
необходимо сравнивать различные уровни, которые относятся либо к различным
периодам времени, либо к плановому заданию, либо к различным территориям. В
связи с этим различают базисный период (период, к которому относится величина,
подвергаемая сравнению) и отчетный период (период, к которому относится
сравниваемая величина). При исчислении важно правильно выбрать период,
принимаемый за базу сравнения.
Индексы
могут относиться либо к отдельным элементам сложного экономического явления,
либо ко всему явлению в целом.
В
зависимости от степени охвата подвергнутых обобщению единиц изучаемой
совокупности индексы подразделяются на индивидуальные (элементарные) и общие.
Индивидуальные
индексы характеризуют изменения отдельных единиц статистической совокупности.
Так, например, если при изучении оптовой реализации продовольственных товаров
определяются изменения в продаже отдельных товарных разновидностей, то получают
индивидуальные (однотоварные) индексы.
В
статистической практике принято следующее обозначение
i
– индивидуальный индекс I – общий индекс
p
– цена q — количество
t
– затраты времени на производство единицы продукции
T
– численность f – з/п
F
– фонд з/п z- себестоимость
pq
– товарооборот, выручка.
zq
– затраты на производство всей продукции
Общие
индексы выражают сводные (обобщающие) результаты совместного изменения всех
единиц, образующих статистическую совокупность.
Рассмотрим
построение общего индекса на примере вычисления индекса товарооборота
(табл.2.1):
Таблица
2.1
|
Наименование товара |
Продано |
Цена за единицу, руб. |
Стоимость проданных товаров |
|||||
|
Базисный период |
Отчетный период |
|||||||
|
Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
по ценам базисного периода |
по ценам отчетного периода |
по ценам базисного периода |
по ценам отчетного периода |
|
|
q0 |
q1 |
p0 |
p1 |
p0q0 |
p1q0 |
p0q1 |
p1q1 |
|
|
А, шт |
2000 |
25000 |
0,15 |
0,10 |
3000 |
2000 |
3750 |
2500 |
|
Б, кг |
16500 |
18500 |
0,20 |
0,12 |
3300 |
1980 |
3700 |
2200 |
|
В, л |
18000 |
24000 |
0,25 |
0,30 |
4500 |
5400 |
6000 |
7200 |
|
ИТОГО |
10800 |
9380 |
13450 |
11900 |
Общее
изменение товарооборота стоимости проданных товаров можно определять,
сопоставив общую стоимость проданных товаров в отчетном периоде по ценам
отчетного периода с общей стоимостью проданных товаров в базисном периоде по
ценам базисного периода:
|
Ipq= |
11900 |
=1,102 |
или |
110,2% |
|
10800 |
Следовательно,
товарооборот в нашем примере увеличился в отчетном периоде по сравнению с
базисным на 10,2% или в абсолютном выражении товарооборот увеличился на 11900 –
10800=1100 руб.
Таким
образом, можно записать формулу общего индекса товарооборота:
|
Ipq= |
∑p1q1 |
(2.1) |
||||
|
∑p0q0 |
||||||
Приведенная
формула индекса товарооборота называется агрегатной (от лат.aggrego-
присоединяю). Агрегатными называются индексы, числители и знаменатели которых
представляют собой суммы, произведения или суммы произведений уровней
изучаемого явления. [6 с.107]
Агрегатная
форма индекса является основной, наиболее распространенной формой экономических
индексов.
Для
исчисления агрегатных индексов необходимы два рода показателей: индексируемые
величины и веса. Но практически эти показатели имеются не всегда. В таких
случаях для удобства расчётов (в том случае, если мы располагаем значениями
индивидуальных индексов) на практике удобно использовать средние индексы.
2.2. Средний арифметический индекс.
Помимо
агрегатных индексов в статистике применяются средневзвешенные индексы. К их
исчислению прибегают тогда, когда имеющаяся в распоряжении информация не
позволяет рассчитать общий агрегатный индекс.
Средний
индекс — это индекс, вычисленный как средняя величина из индивидуальных индексов.
Он должен быть тождествен агрегатному индексу. При исчислении средних индексов
используются две формы средних: арифметическая и гармоническая.
Среднеарифметический индекс тождествен агрегатному, если весами индивидуальных
индексов будут слагаемые знаменателя агрегатного по формуле средней
арифметической, будет равна агрегатному индексу.
Рассмотрим
преобразование агрегатного индекса в среднеарифметический на примере
агрегатного индекса физического объема товарооборота. В этом случае
индивидуальные индексы должны быть взвешены на базисные соизмерители. Из
индивидуального индекса физического объема товарооборота следует, что q1= iqq0. Заменив q1 в числителе
агрегатного индекса физического объема товарооборота (2.4) на iqq0, получим
среднеариметический индекс физического объема продукции:
|
(2.6) |
||||||||
Среднеарифметический индекс трудоемкости
производства продукции определяется следующим образом:
|
It= |
∑itT0 |
= |
∑itt0q0 |
(2.7) |
||
|
∑T0 |
∑t0q0 |
Поскольку
it · to= t1, то формула этого индекса может быть преобразована в агрегатный
индекс трудоемкости продукции. Весами являются общие затраты времени на
производство продукции или численность работников в базисном периоде.
В
статистике широко известен и среднеарифметический индекс производительности
труда. Он носит название индекса Струмилина и определяется следующим образом:
|
It= |
∑itT1 |
(2.8) |
||||
|
∑T1 |
Индекс
показывает, во сколько раз возросла (уменьшилась) производительность труда или
сколько процентов составил рост (снижение) производительности труда в среднем
по всем единицам исследуемой совокупности.
Среднеарифметические
индексы чаще всего применяются на практике для расчета сводных индексов количественных
показателей.
2.3. Средний гармонический индекс.
В
тех случаях, когда не известны отдельные значения p1 и q1, а дано их
произведение р1q1 – товарооборот отчетного периода и индивидуальные индексы цен
ip=р1/q1, а сводный индекс должен быть вычислен с отчетными весами, применяется
среднегармонический индекс цен. Причем индивидуальные индексы должны быть
взвешены таким образом, чтобы среднегармонический индекс совпал с агрегатным.
Из формулы ip=р1/р0 определим неизвестное р0 значение и, заменив в формуле
агрегатного индекса цен (2.2) значение р0=р1/ip, получим среднегармонический
индекс цен: 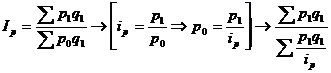
Таким
образом, весами при определении среднегармонического индекса себестоимости
являются издержки производства текущего периода, а при расчете индекса цен
стоимость продукции этого периода.
Применение
той или иной формулы индекса зависит от имеющейся в
распоряжении
информации. Также нужно иметь в виду, что агрегатный индекс может быть преобразован
и рассчитан как средний из индивидуальных Индексов только при совпадении
перечня видов продукции или товаров (их ассортимента) в отчетном и базисном
периодах, т.е. когда агрегатный индекс построен по сравнимому кругу единиц
(агрегатные индексы качественных показателей и агрегатные индексы объемных
показателей при условии сравнимого ассортимента). По несравнимой продукции
нельзя определить индивидуальные индексы, а потому становится невозможным
преобразование агрегатного индекса в адекватные ему средние индексы.
Рассмотрим
применение среднего индекса цен на примере.
Пусть
имеются данные о продаже товаром в магазине (табл.2.2.)
Таблица
2.2.
Данные
о продаже товаров
|
Товар, ед.изм. |
Продано в отчетном периоде p1q1, тыс.руб. |
Изменение цен на товары в отчетном периоде по сравнению с базисным, % |
|
Туфли мужские, пары |
186 |
+3 |
|
Костюмы, шт. |
214 |
+6 |
|
ИТОГО |
400 |
— |
Определить
общий кодекс цен.
Решение.
Запишем, исходя из условия, индивидуальные индексы цен: iⁿp=1,06 и i′p=1,03
и подставим их значения в формулу среднего гармонического индекса цен (2.8):
|
Ip= |
∑p1q1 |
= |
186+214 |
= |
400 |
= |
1,046 |
или |
104,60% |
|
|
∑ |
p1q1 |
186 |
+ |
214 |
382,47 |
|||||
|
ip |
1,03 |
1,06 |
Следовательно,
в отчетном периоде по сравнению с базисным цены на данную группу товаров
повысился в среднем на 4,6% . [3 с.163]
2.4. Базисные и цепные индексы
В
ходе экономического анализа изменение индексируемых величин часть изучают не за
два, за ряд последовательных периодов. Возникает необходимость построения
индексов за ряд этих последовательных периодов.
В
зависимости от выбора базы сравнения индексы бывают цепными и базисными.
В
системе базисных индексов сравнения уровней индексируемого показателя в каждом
индексе производится с уровнем базисного периода, а системе цепных индексов
уровни индексируемого показателя сопоставляются с уровнем предыдущего периода.
Цепные
и базисные индексы могут быть как индивидуальные, так и общие.
Ряды
индивидуальных индексов просты по построению:
|
· базисные индексы |
Ip= |
p1 |
; |
Ip= |
p2 |
; |
Ip= |
p3 |
; |
Ip= |
pn |
. |
|
|
р0 |
р0 |
р0 |
р0 |
||||||||||
|
· цепные индексы |
Ip= |
p1 |
; |
Ip= |
p2 |
; |
Ip= |
p3 |
; |
Ip= |
pn |
. |
|
|
р0 |
р1 |
р2 |
pn-1 |
Между
цепными и базисными индивидуальными индексами существует взаимосвязь —
произведение последовательных цепных индивидуальный индексов дает базисный
индекс последнего периода:
|
Ip= |
p1 |
* |
p2 |
* |
p3 |
* |
pn |
= |
pn |
|
р0 |
р1 |
р2 |
рn-1 |
р0 |
Отношение
базисного индекса отчетного периода к базисному индексу предшествующего периода
дает цепной индекс отчетного периода:
|
Ip= |
pn |
: |
рn-1 |
= |
pn |
|
р0 |
р0 |
рn-1 |
|||
Это
правило позволяет применять так называемый цепной метод, т.е находить
неизвестный ряд базисных индексов по известным цепным, и наоборот.
Рассмотрим
построение базисных и цепных индексов на примере агрегатных индексов цен и
физического объема продукции. Известно, что если строится ряд индексов, то веса
в нем могут быть либо постоянными для всех индексов ряда, либо переменными.
Базисные индексы
Индексы
цен Паше (с переменными весами):
|
IР1/0= |
∑p1q1 |
; |
IP2/0= |
∑p2q2 |
; |
…; |
IPn/0= |
∑pnqn |
; |
|
∑p0q1 |
∑p0q2 |
∑p0qn |
Индексы
цен Ласпейреса (с постоянными весами)
|
IP1/0= |
∑p1q0 |
; |
IP2/0= |
∑p2q0 |
; |
…; |
IPn/0= |
∑pnq0 |
; |
|
∑p0q0 |
∑p0q0 |
∑p0q0 |
Индексы
физического объема продукции (с постоянными весами):
|
Iq1/0= |
∑p1q0 |
; |
Iq2/0= |
∑p2q0 |
; |
…; |
Iqn/0= |
∑qnp0 |
; |
|
∑p0q0 |
∑p0q0 |
∑p0q0 |
Цепные
индексы
Индексы
цен Паше (с переменными весами):
|
IР1/0= |
∑p1q1 |
; |
IP2/1= |
∑p2q2 |
; |
…; |
IPn/n-1= |
∑pnqn |
; |
|
∑p0q1 |
∑p1q2 |
∑pn-1qn |
Индексы
цен Ласпейреса (с постоянными весами)
|
IP1/0= |
∑p1q0 |
; |
IP2/1= |
∑p2q0 |
; |
…; |
IPn/n-1= |
∑pnq0 |
|
∑p0q0 |
∑p1q0 |
∑pn-1q0 |
Индексы
физического объема продукции (с постоянными весами):
|
Iq1/0= |
∑p1q0 |
; |
Iq2/1= |
∑q2p0 |
; |
…; |
Iqn/n-1= |
∑qnp0 |
. |
|
∑q0p0 |
∑q1p0 |
∑qn-1p0 |
Итак,
в базисных агрегатных индексах все отчетные данные сопоставляются только с
базисными (закрепленными) данными, а в цепных – с предыдущими (в данном случае
– смежными) данными.
Ряды
агрегатных индексов с постоянными весами имеют преимущество – сохраняется
взаимосвязь между цепными и базисными индексами, например, в ряду агрегатных
индексов физического объема:
|
∑q1p0 |
* |
∑q2p0 |
* |
∑q3p0 |
= |
∑q3p0 |
|
∑p0q0 |
∑q1p0 |
∑q2p0 |
∑p0q0 |
или
в ряду агрегатных индексов цен Ласпейреса:
|
∑p1q0 |
* |
∑p2q0 |
* |
∑p3q0 |
= |
∑p3q0 |
|
∑p0q0 |
∑p1q0 |
∑p2q0 |
∑p0q0 |
Таким
образом, использование постоянных весов в течение ряда лет позволяет переходить
от цепных общих индексов к базисным, и наоборот.
В
рядах агрегатных индексов качественных показателей, которые строятся с
переменными весами (например, ряд цен Паше), перемножение цепных индексов не
дает базисный:
|
∑p1q1 |
* |
∑p2q2 |
* |
∑p3q3 |
≠ |
∑p3q1 |
|
∑p0q1 |
∑p1q2 |
∑p2q3 |
∑p0q1 |
Для
таких индексов переход от цепных индексов к базисным, и наоборот невозможен. Но
в статистической практике часто возникает необходимость определения динамики
цен за длительный период времени на основе цепных индексов или с переменными
веса. Тогда для получения приближенного итогового индекса цепные индексы цен
перемножают, заведомо зная, что в таком расчете допускается ошибка. Отчетные
индексы этого ряда используются для пересчета стоимостных показателей отчетного
периода в ценах предыдущего года.
III. Практическая часть
Второй
вариант.
ЗАДАЧА
I.
Имеются
следующие данные о стаже работы и проценты выполнения норм выработки рабочих-сдельщиков
за отчетный месяц:
|
Рабочий, № п/п |
Стаж, число лет |
Выполнение норм, % |
Рабочий, № п/п |
Стаж, число лет |
Выполнение норм, % |
|
1 |
1,0 |
96 |
11 |
10,5 |
108 |
|
2 |
6,5 |
103 |
12 |
9,0 |
107 |
|
3 |
9,2 |
108 |
13 |
5,0 |
105 |
|
4 |
4,5 |
103 |
14 |
6,0 |
103 |
|
5 |
6,0 |
106 |
15 |
10,2 |
109 |
|
6 |
2,5 |
100 |
16 |
5,4 |
102 |
|
7 |
2,5 |
101 |
17 |
7,5 |
105 |
|
8 |
16,0 |
113 |
18 |
8,0 |
106 |
|
9 |
14,0 |
110 |
19 |
8,5 |
106 |
|
10 |
12,0 |
109 |
20 |
11,0 |
107 |
Для
выявления зависимости между стажем работы и выполнением норм выработки
произвести группировку рабочих по стажу, образовав пять групп с равными интервалами.
По
каждой группе и совокупности рабочих подсчитайте: 1) число рабочих; 2) средний
стаж работы; 3) средний процент выполнения норм выработки.
Результаты
оформите в групповой таблице и сделайте выводы.
РЕШЕНИЕ:
В
качестве группировочного признака возьмем стаж рабочих. Образуем пять групп
рабочих с равными интервалами. Величину интервала определим по формуле:
хmax
— xmin 16-1
h=
_____________ = _________= 3 число лет
n
5
Обозначим
границы групп:
1
– 4 – 1-я группа;
4
– 7 – 2-я группа;
7
– 10 – 3-я группа;
10
– 13 – 4-я группа;
13
– 16 – 5-я группа.
После
того, как определен группировочный признак, задано число групп и образованы
сами группы, необходимо отобрать показатели, которые характеризуют группы, и
определить их величины по каждой группе. Результаты разносим в таблицу 3.1.
Таблица
3.1
|
№ группы |
Группы рабочих по стажу работы |
Число рабочих |
Средний стаж работы, число лет |
Средний процент выполнения норм выработки, % |
|
1 |
1 – 4 |
3 |
2 |
99 |
|
2 |
4 – 7 |
6 |
5,6 |
103,7 |
|
3 |
7 – 10 |
5 |
8,4 |
106,4 |
|
4 |
10 – 13 |
4 |
10,9 |
108,3 |
|
5 |
13 – 16 |
2 |
15 |
111,5 |
|
ИТОГО |
20 |
Вывод.
Таким
образом, чем больше стаж работы, тем выше процент выполнения норм выработки.
ЗАДАЧА
II.
Имеются
следующие данные о реализации товаров на городском колхозном рынке:
|
Товар |
Средняя цена единицы товара, руб. |
Количество проданного товара, тыс. |
||
|
январь |
март |
январь |
март |
|
|
Картофель, кг |
4,0 |
5,0 |
50 |
52 |
|
Молоко, л |
8,0 |
10,0 |
15 |
20 |
Определите
общие индексы: 1) товарооборота; 2) физического объема товарооборота; 3) цен и
сумму экономии (или перерасхода) от изменения цен.
Покажите
взаимосвязь между исчисленными индексами.
РЕШЕНИЕ:
1)
Рассчитаем сводный индекс цен по формуле (2.2):
где
р1 — средняя цена, руб. в отчетном периоде;
р0
– средняя цена, руб. в базисном периоде;
q1
–количество проданного товара, тыс. в отчетном периоде.
52*5,0+20*10,0 260+200 460
Ip
=——————— = —————= ——— = 1,25 125%
52*4,0+20*8,0
208+160 368
Применение
формулы 1 показывает, что в целом цены повысились в среднем на 25%.
2)
Рассчитаем сводный индекс физического объема реализации по формуле (2.4):
где
р0 – средняя цена, руб. в базисном периоде;
q0
–количество проданного товара, тыс. в базисном периоде;
q1
–количество проданного товара, тыс. в отчетном периоде.
52*4,0+20*8,0
208+160 368
Ip =——————— = —————=
——— = 1,15 115%
15*8,0+50*4,0
120+200 320
Применение
формулы 2 показывает, что по данному ассортименту товаров в целом прирост
физического объёма реализации в текущем периоде составил в среднем 15%.
3)
Определяем индекс товарооборота по формуле (3.1)
где
Ip – сводный индекс цен;
Iq
– сводный индекс физического объема реализации
Ipq = 1,25 ∙ 1,15 = 1,4375 143,75%
или
по формуле: pq= (3.2)
где
р0 – средняя цена, руб. в базисном периоде;
q0
–количество проданного товара, тыс. в базисном периоде;
q1
–количество проданного товара, тыс. в отчетном периоде;
р1
— средняя цена, руб. в отчетном периоде.
52*5,0+20*10,0
260+200 460
Ipq = ——————- =
———— = —— = 1,4375 143,75%
15*8,0+50*4,0
120+200 320
За
счет увеличения физического объема товарооборота на 15% и за счет увеличения
цены на 25% товарооборот увеличился на 43%
4)
Определим абсолютный прирост товарооборота (разница между числителем и
знаменателем индекса товарооборота):
Ipq
= —
= 460 — 320=
140 руб.
Товарооборот
возрос в отчетном периоде по сравнению с базисным, а также величина экономии
составила 140 рублей.
Определяем
за счет, каких факторов это произошло.
а)
за счет изменения цен.
Ip
= —
= 460 – 368 =
92 руб.
За
счет роста цен товарооборот возрос на 92 рубля.
б)
за счет изменения объема продаж
Ip
= —
= 368 – 320=
48 руб.
Товарооборот
увеличился за счет увеличения объема продаж на 48 рублей.
Общее
изменение товарооборота
140
руб. = (92руб. + 48руб.)
ЗАДАЧА
III.
Выполняйте
по показателю 2, приведенному в таблице исходных данных.
|
№ показателя, соответствующего номеру |
2002 |
2003 |
2004 |
2005 |
2006 |
|
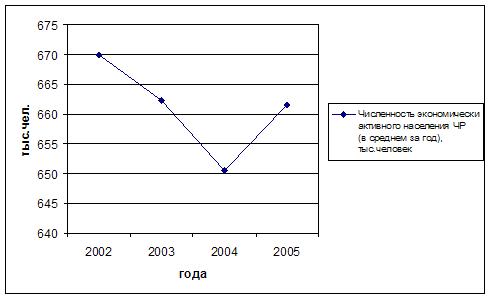
2. Численность экономически активного |
670,0 |
662,3 |
650,5 |
661,6 |
Для
анализа динамики соответствующего показателя вычислить:
1)
абсолютные приросты (снижения), темпы роста и прироста (снижения) по годам и по
сравнению с 2002 г., абсолютное содержание одного процента прироста (снижения).
Результаты представить в виде таблицы;
2)
среднегодовой уровень и среднегодовой абсолютный прирост (снижение);
3)
среднегодовой темп роста и темп прироста.
4)
Построить график. Сделать выводы.
РЕШЕНИЕ:
1)
Для вычисления абсолютных приростов (снижений), темпов роста и прироста
(снижения) по годам и по сравнению с 2002 г., абсолютного содержания одного
процента прироста (снижения), используем нижеприведенные формулы:
Цепной
абсолютный прирост — (3.3)
Базисный
абсолютный прирост — (3.4)
Цепные
темпы роста: *100 (3.5)
Базисные
темпы роста: *100 (3.6)
Цепные
темпы прироста: или
К0 = К0 — 100
% (3.7)
Базисные
темпы прироста: или
Ка = Ка — 100
% (3.8)
Абсолютное
значение (содержание) одного процента прироста:
где
и
— абсолютный
базисный или цепной прирост;
— уровень ряда
динамики, выбранный за базу для определения базисных абсолютных приростов;
— уровень ряда динамики, выбранный за базу для
определения i-го цепного абсолютного прироста
Результаты
вычислений представлены в Приложении 1.
2)
Рассчитаем среднегодовой уровень прироста (снижения). Для вычисления используем
формулу:
yпр=
∑y / n (3.10)
где
у – абсолютные уровни ряда;
n-
число уровней ряда.
yпр=
(670+662,3+650,5+661,6) / 4= 2644,4/ 4 = 661,1 тыс.чел.
Для
вычисления среднегодового абсолютного прироста (снижения) используем формулы:
∆y1=∑∆y1/
n (3.11)
∆y0=∑∆y0/
n (3.12)
где
n- число абсолютных приростов цепных или базисных;
∆y1-цепные
абсолютные приросты;
∆y0-базисные
абсолютные приросты
∆y1=
(-7,7+-11,8+11,8) / 3 = -8,4/3=-2,8 тыс. чел.
∆y1=
(-7,7+-19,5+-8,4) / 3 = -35,6/3=-11,87 тыс. чел.
3)
Рассчитаем среднегодовой темп роста и прироста, %:
Тр=3√661,6
/ 670= 3√0,987= 3√987*3√10-3= 9,96* 10=0,996 = 99,6%
Следовательно,
среднегодовой темп сокращения численности экономически активного населения ЧР
составил:
Тпр=
Тр-100= 99,6 – 100= -0,4%
4)
График «Численность экономически активного населения ЧР (в среднем за год),
тыс. человек» представлен на рисунке 3.2
Рис.
3.2. Численность экономически активного населения ЧР,тыс. человек
На
рисунке 3.3 представлен график «Абсолютный прирост экономически активного
населения ЧР (в среднем за год), тыс. человек».
Рис.
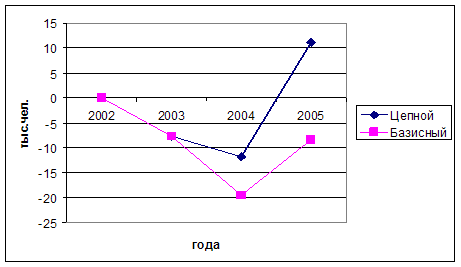
3.3. Абсолютный прирост экономически активного населения ЧР, тыс. человек
На
рисунке 3.4 представлен график «Абсолютное значение одного процента прироста,
%»
Рис.
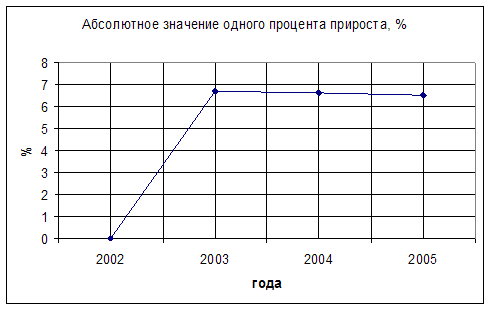
3.4 Абсолютное значение одного процента прироста, %
4.
Список используемой литературы:
Бендина
Н.В. Общая теория статистики (конспект лекций).- М.: Финансы и статистика, 2002
Воронин
В.Ф., Жильцова Ю.В.Статистика. –М.: Экономистъ, 2004.
Гусаров
В.М. Статистика. М.: ЮНИТИ-ДАНА, 2003
Елисеева
М.А. Общая теория статистики, М.: Статистика, 1988.
Финансы.
Под ред. В.М. Родионовой. – М.: Финансы и статистика, 1994.
Харченко
Н.М. Статистика: Учебник.-М.: Издательство-торговая корпорация «Дашков и К0»,
2007.
Шмайлова
Р.А. Практикум по теории статистики. – М.:Финансы и статистика, 1999.
Список литературы
Для
подготовки данной работы были использованы материалы с сайта http://referat.ru
|
А= |
yi-yi-1 |
= |
yi-1 |
= |
0,01 yi-1% |
(3.9) |
||||||
|
yi-yi-1 |
* |
100 |
100 |
|||||||||
|
yi-1 |
Дата добавления: 24.03.2008