Среднегодовой темп роста применяется при анализе рядов динамики для выявления общей тенденции изменения показателя во времени.
Как видно из названия – это усредненный показатель. Его значение говорит о том, что если бы каждый год темп роста был одинаковым и равен среднему, то общий рост показателя был равен фактическому.
Среднегодовой темп роста можно определить двумя способами:
- Tp‾=yny1n−1∗100%overline{T_p}=sqrt[n-1]{frac{y_n}{y_1}}*100%,
где yny_n — значение показателя отчетного периода;
y1y_1 — значение показателя базового периода;
nn — количество лет.
- Tp‾=Kp2∗Kp3∗…∗Kpnn−1∗100%overline{T_p}=sqrt[n-1]{K_p^2*K_p^3*…*K_p^n}*100%,
где KpiK_p^i — цепной коэффициент роста за i-й период.
Примеры решения задач
Пример 1
В 2010 году на предприятии было выпущено продукции на 3650 тыс. руб., а в 2017 — на 4251 тыс. руб. Найти среднегодовой темп роста выпуска продукции.
Решение
Tp‾=425136508−1∗100%=102,2%overline{T_p}=sqrt[8-1]{frac{4251}{3650}}*100%=102,2%
В среднем за год выпуск продукции возрастал на 2,2%.
Ответ: Tp‾=102,2%overline{T_p}=102,2%
Пример 2
Рассчитать среднегодовой темп роста с использованием коэффициентов роста.
| Год | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|
| Объем выпуска, тыс. шт. | 1020 | 1021 | 1300 | 1250 | 1280 | 1310 | 1390 | 1460 |
Решение
Решим данную задачу средствами MS Excel.
Коэффициент роста определяется как отношение показателя текущего года к предыдущему.
Получаем
Далее необходимо получить произведение этих коэффициентов.
Извлекаем корень 7-й степени. Это возможно двумя путями
Или
Также среднегодового темпа роста при помощи средней геометрической
Получили
Ответ: 105,26%.
Не можешь разобраться в этой теме?
Обратись за помощью к экспертам
Гарантированные бесплатные доработки
Быстрое выполнение от 2 часов
Проверка работы на плагиат
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
- Общая формула темпа роста
- Темп роста прибыли
- Темп прироста
- Темп роста выручки
- Базисный и цепной темпы роста
- Считаем темп роста по формуле CAGR
- Чем опасны быстрые и медленные темпы
- Каким должен быть идеальный темп
- Рассчитываем пошагово устойчивый рост прибыли
- Итоги
Общая формула темпа роста
Формула в целом используется для оценки развития и роста экономики. Она может применяться для изучения быстроты увеличения доходов, объемов продаж, численности сотрудников в компании и т. п.
Общий вид формулы:
Темп роста = Текущее значение / Предыдущее значение х 100%
С ее помощью рассматривают скорость изменения определенной величины на определенный период времени. Тем самым определяют динамику развития системы и принимают соответствующие меры.
Далее на конкретных примерах мы покажем, как она работает. Сейчас же отметим:
- если темп больше 100%, это говорит об увеличении показателя;
- если полученное значение равно 100%, то уровень остался неизменным;
- когда меньше 100%, это значит, исследуемый показатель уменьшился к началу периода.
Темп роста прибыли
Прибыль — это сумма, которая остается у компании от дохода после покрытия всех затрат. И ее важно отслеживать в динамике.
Для оценки степени роста прибыли в течение определенного периода времени используют формулу:
Темп роста прибыли = Прибыль текущего периода / Прибыль предыдущего периода × 100%
Темп показывает, сколько процентов один показатель составляет относительно другого.
К примеру, чистая прибыль небольшой фирмы — 40 тыс. рублей в марте и 45 тыс. рублей в апреле. Считаем по формуле:
45 000 / 40 000 × 100 = 112 500. То есть, в апреле к марту индекс роста прибыли составил 112,5%.
Другой пример, показывающий, что у компании есть трудности с получением прибыли:
300 000 / 368 000 × 100 = 81,5%
Как видно, знание темпов роста прибыли компании нужно для анализа ее финансового состояния. По нему инвесторы смогут принимать решение о вложениях в предприятие. А менеджеры — разрабатывать стратегии по увеличению прибыли фирмы, определять направления, которые позволят улучшить ее финансовые показатели.
Как отмечает Сергей Гебель, генеральный директор юридической компании «Гебель и партнеры», благодаря расчету темпов роста прибыли можно оценить, насколько эффективно работает компания, спрогнозировать будущие показатели и провести сравнение с ближайшими конкурентами:
«Проанализировав тенденцию за несколько лет, можно выявить как положительные, так и отрицательные факторы, влияющие на рост, и учесть их в будущем. При этом нужно понимать, что темп роста не является абсолютным показателем, поскольку прибыль может быть подвержена влиянию разовых непредвиденных факторов», — отмечает эксперт.
Отметим, что для измерения роста прибыли используются показатели EBITDA, EBIT и OIBDA.
EBITDA указывает на прибыль компании до учета различных расходов, таких как амортизация, проценты по заемным средствам и налоги. Он используется для оценки финансовой устойчивости компании и ее потенциала для генерации прибыли.
EBIT — показатель прибыли, который учитывает все расходы, кроме процентов по заемным средствам и налогов. Он показывает, сколько прибыли компания получила от своей операционной деятельности.
OIBDA — содержит операционную прибыль, не учитывая неоперационные доходы и расходы. Позволяет оценить эффективность операционной деятельности компании без учета неоперационных расходов.
«В моем доме попрошу не выражаться!» Что такое на самом деле эта ЕБИТДА
Темп прироста
Темп прироста прибыли показывает конкретное число, насколько быстро прибыль растет или уменьшается по сравнению с предыдущим периодом.
Для расчета темпов прироста используют две формулы, какая удобнее — выбираете сами. Если ответ получится со знаком минус, это значит, в указанный период темпы прироста снизились.
В расчетах используем те же значения, что и в первом примере.
Темп прироста = Текущее значение / Базовое значение × 100% – 100%:
45 000 / 40 000 × 100% − 100% = 12,5%
Темп прироста = (Текущее значение − Базовое значение) / Базовое значение × 100%:
(45 000 − 40 000) / 40 000 × 100 % = 12,5%
Как видим, темп прироста показывает, на сколько процентов увеличился показатель.
Темп роста выручки
Выручка — это доход, полученный компанией за определенный период времени, включающий в себя доходы от продаж, инвестиций и прочие поступления. Это то, сколько денег получила компания от своей деятельности без учета расходов.
Когда требуется проанализировать темп роста выручки, применяют формулу:
Рост выручки = Текущая выручка / Предыдущая выручка × 100%
Формула позволяет определить, на сколько процентов выручка изменилась за данный период. Уточним, что «Текущая выручка» и «Предыдущая выручка» представляют собой соответствующие значения выручки за определенный период времени (например, месяц, квартал, год).
Возвращаясь к примеру с небольшой фирмой, допустим, что выручка за март у нее составила 55 тыс. рублей, а за апрель — 60 тыс. рублей. Подставим эти значения в формулу:
60 000 / 55 000 × 100% = 109%
В нашем случае положительное значение говорит о том, что компания растет и увеличивает свой доход. Если же получается отрицательное число — это говорит о снижении выручки и потенциальных проблемах в бизнесе.
Чтобы открыть свое дело, требуется стартовый капитал. Взять его можно, воспользовавшись выгодными кредитом в Совкомбанке!
Если вы горите идеей об открытии своего бизнеса, мы можем помочь вам! В Совкомбанке доступны кредиты для предпринимателей до 30 млн рублей. Вы составили бизнес-план и знаете, сколько средств вам понадобится для открытия собственного бизнеса? Смело рассчитывайте кредит и ежемесячный платеж по нему на нашем специальном калькуляторе!
Рассчитать кредит
Базисный и цепной темпы роста
Различают базисный и цепной темпы роста прибыли. Базисный — все периоды сравниваются с показателем на начало периода.
Когда же для вычисления темпа роста используется текущее значение к предыдущему, но не к базисному, показатель называют цепным.
Вспомним, как идут дела у нашей маленькой фирмы из примера. Допустим, мы хотим просчитать базисный и цепной темпы роста ее выручки за 2023 год по месяцам.
Условимся, что в январе выручка компании составила 40 тыс. рублей, в феврале — 45 тыс. рублей, в марте — 55 тыс. рублей, в апреле — 60 тыс. рублей.
Согласно формуле:
Рост выручки = Текущая выручка / Предыдущая выручка × 100%
Базисные темпы роста составят:
Февраль: 45 000 / 40 000 × 100% = 112,5%
Март: 55 000 / 40 000 × 100% = 137,5%
Апрель: 60 000 / 40 000 × 100% = 150%
Цепные:
Февраль: 45 000 / 40 000 × 100% = 112,5%
Март: 55 000 / 45 000 × 100% = 122,2%
Апрель 60 000 / 55 000 × 100% = 109,9%
Базисный метод лучше использовать, когда в компании случились какие-то изменения, выбранные за точку отсчета. Например, произошел ребрендинг, появились новые рынки сбыта и т. п.
Цепной метод применяют, когда в компании не происходило каких-либо значимых изменений на протяжении большого отрезка времени.
Считаем темп роста по формуле CAGR
Формула CAGR (Compound Annual Growth Rate) используется для расчета среднегодового темпа роста. Эта формула позволяет определить, какая была бы годовая ставка роста на протяжении указанного периода времени, если бы рост был равномерным и составил одинаковый процент в каждый год.
Формула CAGR выглядит следующим образом:
CAGR = (FV/PV)^(1/n) — 1,
где:
FV — конечное значение прибыли,
PV — начальное значение прибыли,
n — количество лет.
Допустим, в 2020 году прибыль компании составляла 1 млн рублей, а в 2023 году она увеличилась до 1,5 млн рублей. Найдем среднегодовой темп роста за этот период:
CAGR = (1 500 000 / 1 000 000)^(1 / 3) – 1 = 14,47%
Таким образом, средняя годовая ставка роста прибыли за последние 3 года составила 14,47%.
Расчет CAGR позволяет оценить темп роста компании и сравнить его со средними темпами роста отрасли или рынка. Эта формула также используется для прогнозирования будущих доходов и оценки рентабельности инвестиций.
Поскольку возведение в степень может вызвать трудности, лучше использовать онлайн-калькулятор, который можно найти в интернете по соответствующему запросу.
Чем опасны быстрые и медленные темпы
Быстрые темпы роста прибыли обеспечивают успех организации и позволяют ей приобретать новые активы, расширять операционную деятельность и увеличивать прибыль в долгосрочной перспективе. Такой компании легче привлекать инвестиции.
Обратная сторона медали — быстрые темпы роста могут привести к переоценке активов компании и к нереалистичным ожиданиям со стороны инвесторов.
Еще это может стать причиной переинвестирования прибыли в нерентабельные или неперспективные проекты, которые приведут к большими финансовым потерям в будущем.
Снижение темпов роста прибыли и иных показателей, падение производства грозит тем, что со временем компания начнет работать в «минус», пытаясь поддерживать минимальный уровень постоянных затрат, в то время как ее производственные объемы снижаются.
Если суммировать положительные результаты быстрых темпов роста прибыли, это означает:
- увеличение доходов и прибыли компании;
- расширение рынка и укрепление позиций на нем;
- привлечение внимания инвесторов и повышение оценки компании на фондовом рынке;
- возможность инвестирования в новые проекты и технологии, что позволяет снизить риски и увеличить конкурентоспособность.
Минусы быстрых темпов роста прибыли:
- риск банкротства из-за неспособности справиться с ростом долговых обязательств;
- ухудшение качества продукции и услуг из-за снижения контроля над производственными процессами;
- снижение лояльности клиентов из-за недостаточного качества обслуживания;
- риск диверсификации компании и потери фокусировки на основном продукте или услуге;
- негативный имидж из-за неэтичного поведения (например, нарушения прав работников или негативного влияния на экологию).
Как подчеркивает Сергей Гебель, для любой компании оптимальным является темп, способный обеспечить устойчивый рост на протяжении длительного времени:
«Стремление обеспечить чрезмерно высокий темп прибыли может стать причиной несбалансированности стратегических задач с политикой финансирования.
Следует отметить, что высокие темпы роста в прошлом не гарантируют, что они будут постоянно сохраняться в будущем.
В свою очередь, слишком низкий темп роста может говорить о неэффективности компании и нерациональном использовании имеющегося капитала».
Каким должен быть идеальный темп
Чтобы стремление компании увеличивать прибыль максимально быстро не приводило к нежелательным последствиям, важно определить идеальный темп роста. То есть, прибыль должна расти на такую скорость, чтобы компания могла оптимально развиваться, сохранять конкурентную позицию в отрасли и удерживать инвесторов.
Золотым правилом экономики является темп роста прибыли, который превосходит изменения уровня продаж и темп изменения итогового баланса. Это правило выражается в соотношении:
Тбп > Топ > Та > 100%,
где:
Тбп — темп изменения балансовой прибыли (до налогообложения, которая была получена от всех видов своей хозяйственной деятельности);
Топ — темп изменения уровня продаж;
Та — темп изменения итога (валюты) баланса, то есть суммы всех активов или всех пассивов, которые отражены в балансе.
Если показатели имеют значения, которые соответствуют соотношению Тбп > Топ > Та > 100%, это значит, что компания находится в идеальном состоянии, так как ее прибыль растет быстрее, чем уровень продаж и итог баланса. Это является показателем успешности бизнеса.
В период расширения или модернизации предприятия соотношение может нарушиться, но это не говорит о том, что в перспективе предприятие столкнется проблемами в экономике.
Увеличить объем продаж можно с помощью надежного партнера.
Не знаете, как увеличить продажи? Станьте партнером Халвы и получите лояльных клиентов, целевой трафик и дополнительный товарооборот. Оставьте заявку на сайте Совкомбанка и продавайте еще больше.
Рассчитываем пошагово устойчивый рост прибыли
Важный инструмент для определения потенциала развития компании в будущем — расчет устойчивого роста прибыли. Он показывает, на какой максимум прибыли компания может рассчитывать через некоторое время, учитывая ее текущее финансовое состояние и рыночные факторы.
Например, если показатели роста прибыли низкие, это может говорить о недостаточных объемах продаж, о неэффективности процессов производства. Зная о выявленной проблеме, компания сможет сосредоточиться на улучшении проблемных показателей.
Для расчета устойчивого темпа роста прибыли компании используют формулу:
g = roe x dpr,
где:
roe (return on equity) — рентабельность собственного капитала;
dpr (dividend payout ratio) — норма выплаты дивидендов.
1. Чтобы рассчитать рентабельность собственного капитала компании (roe), применяют формулу:
roe = (чистая прибыль / средний объем собственного капитала) x 100%
где:
чистая прибыль — значение за год после уплаты налогов и выплаты дивидендов;
средний объем собственного капитала — сумма собственного капитала на начало и конец года, разделенная на 2.
Например:
Годовая прибыль составляет 100 млн рублей.
Размер собственного капитала в начале года — 500 млн рублей, в конце года — 600 млн рублей.
Находим среднее значение = (500 + 600) / 2 = 550 млн рублей.
И вычисляем roe = (100 / 550) x 100% = 18,18%
2. Норма выплаты дивидендов dpr может быть рассчитана следующей формулой:
dpr = (дивиденды за год / чистая прибыль) x 100%
где:
дивиденды за год — сумма дивидендов, выплаченных за год;
чистая годовая прибыль — прибыль за вычетом налогов и уплаченных дивидендов.
Например:
Дивиденды за год — 25 млн рублей.
Годовая прибыль компании — 100 млн рублей.
dpr = (25 / 100) x 100% = 25%
3. Подставив найденные roe и dpr в формулу, произведем расчет устойчивого темпа роста g:
g = 18,18% x 25% = 4,55%
Такое значение поможет предприятию сохранять свою финансовую устойчивость и выплату дивидендов.
Итоги
Знание темпа роста прибыли помогает понять, насколько успешна деятельность компании и ее стратегия развития. Это позволяет принимать более осознанные решения по управлению бизнесом и предсказывать будущие результаты.
Опираясь на данные по устойчивому росту прибыли, компания может планировать свои финансовые ресурсы и инвестировать в новые проекты: исследования и разработки, маркетинг и расширение бизнеса.
Лучше, когда развитие происходит плавно. Следует придерживаться правил, которые уберегут предприятие от рисков, связанных с чрезмерно быстрым разрастанием.
Средний годовой темп роста и средний годовой темп прироста
Прежде
всего
отметим,
что
приведенные
в
таблице
темпы
роста
( гр.7
и

рядами
динамики
относительных
величин
— производными
от
интервального
ряда
динамики
(гр.2).
Ежегодные
темпы
роста
(гр.7)
изменяются
по
годам
( 105%; 103,8%; 105,5%; 101,7%). Как
вычислить
среднюю
величину
из
ежегодных
темпов
роста
? Эта
величина
называется
среднегодовым
темпом
роста.
Среднегодовой
темп
роста
исчисляется
в
следующей
последовательности:
-
сначала
по
формуле
средней
геометрической
исчисляют
среднегодовой
коэффициент
роста
(снижения)
— -
на
базе
среднегодового
коэффициента
определяют
среднегодовой
темп
роста
()путем
умножения
коэффиицента
на
100%:
Среднегодовой
темп
прироста
( определяется
путем
вычитания
из
темпа
роста
100%.
Среднегодовой
коэффициент
роста
( снижения
) по
формулам
средней
геометрической
может
быть
исчислен
двумя
способами:
1)
на
базе
абсолютных
показателей
ряда
динамики
по
формуле:
-
n —
число
уровней; -
n
— 1 —
число
лет
в
период;
2)
на
базе
ежегодных
коэффициентов
роста
по
формуле
-
m —
число
коэффициентов.
Результаты
расчета
по
формулам
равны,
так
как
в
обеих
формулах
показатель
степени
— число
лет
в
периоде,
в
течение
которого
происходило
изменение.
А
подкоренное
выражение
— это
коэффициент
роста
показателя
за
весь
период
времени
(см.
табл.
11.5, гр.6,
по
строке
за
1998 г.).
Среднегодовой
темп
роста
равен
Среднегодовой
темп
прироста
определяется
путем
вычитания
из
среднегодового
темпа
роста
100%. В
нашем
примере
среднегодовой
темп
прироста
равен
Следовательно,
за
период
1995 — 1998 гг.
объем
производства
продукта
«А»
в
среднем
за
год
возрастал
на
4,0%. Ежегодные
темпы
прироста
колебались
от
1,7% в
1998 г.
до
5,5% в
1997 г.
(за
каждый
год
темпы
прироста
см.
в
табл.
11.5, гр.
9).
Среднегодовой
темп
роста
(прироста)
позволяет
сравнивать
динамику
развития
взаимосвязанных
явлений
за
длительный
период
времени
(например,
среднегодовые
темпы
роста
численности
работающих
по
отраслям
экономики,
объема
производства
продукции
и
др.),
сравнивать
динамику
какого-либо
явления
по
разным
странам,
исследовать
динамику
какого-либо
явления
по
периодам
исторического
развития
страны.
7.
Индексами называют
сравнительные
относительные
величины,
которые
характеризуют
изменение
сложных
социально-экономических
показателей
(показатели,
состоящие
из
несуммируемых
элементов)
во
времени,
в
пространстве,
по
сравнению
с
планом.
Индекс
— это
результат
сравнения
двух
одноименных
показателей,
при
исчислении
которого
следует
различать
числитель
индексного
отношения
(сравниваемый
или
отчетный
уровень)
и
знаменатель
индексного
отношения
(базисный
уровень,
с
которым
производится
сравнение).
Выбор
базы
зависит
от
цели
исследования.
Если
изучается
динамика,
то
за
базисную
величину
может
быть
взят
размер
показателя
в
периоде,
предшествующем
отчетному.
Если
необходимо
осуществить
территориальное
сравнение,
то
за
базу
можно
принять
данные
другой
территории.
За
базу
сравнения
могут
приниматься
плановые
показатели,
если
необходимо
использовать
индексы
как
показатели
выполнения
плана.
Индексы
формируют
важнейшие
экономические
показатели
национальной
экономики
и
ее
отдельных
отраслей.
Индексные
показатели
позволяют
осуществить
анализ
результатов
деятельности
предприятий
и
организаций,
выпускающих
самую
разнообразную
продукцию
или
занимающихся
различными
видами
деятельности.
С
помощью
индексов
можно
проследить
роль
отдельных
факторов
при
формировании
важнейших
экономических
показателей,
выявить
основные
резервы
производства.
Индексы
широко
используются
в
сопоставлении
международных
экономических
показателей
при
определении
уровня
жизни,
деловой
активности,
ценовой
политики
и
т.д.
Существует
два
подхода
в
интерпретации
возможностей
индексных
показателей:
обобщающий
(синтетический)
и
аналитический,
которые
в
свою
очередь
определяются
разными
задачами.
Суть
обобщающего
подхода
— в
трактовке
индекса
как
показателя
среднего
изменения
уровня
исследуемого
явления.
В
этом
случае
основной
задачей,
решаемой
с
помощью
индексных
показателей,
будет
характеристика
общего
изменения
многофакторного
экономического
показателя.
Аналитический
подход
рассматривает
индекс
как
показатель
изменения
уровня
результативной
величины,
на
которую
оказывает
влияние
величина,
изучаемая
с
помощью
индекса.
Отсюда
и
иная
задача,
которая
решается
с
помощью
индексных
показателей:
выделить
влияние
одного
из
факторов
в
изменении
многофакторного
показателя.
От
содержания
изучаемых
показателей,
методологии
расчета
первичных
показателей,
целей
и
задач
исследования
зависят
и
способы
построения
индексов.
По
степени
охвата
элементов
явления
индексы
делят
на
индивидуальные
и
общие
(сводные).
Индивидуальные
индексы (i)
— это
индексы,
которые
характеризуют
изменение
только
одного
элемента
совокупности.
Общий
(сводный)
индекс (I)
характеризует
изменение
по
всей
совокупности
элементов
сложного
явления.
Если
индексы
охватывают
только
часть
явления,
то
их
называют
групповыми.
В
зависимости
от
способа
изучения
общие
индексы
могут
быть
построены
или
как
агрегатные
(от
лат.
аggrega
— присоединяю)
индексы,
или
как
средние
взвешенные
индексы
(средние
из
индивидуальных).
Способ
построения агрегатных
индексов заключается
в
том,
что
при
помощи
так
называемых
соизмерителей
можно
выразить
итоговые
величины
сложной
совокупности
в
отчетном
и
базисном
периодах,
а
затем
первую
сопоставить
со
второй.
В
статистике
имеют
большое
значение
индексы
переменного
и
фиксированного
состава,
которые
используются
при
анализе
динамики
средних
показателей.
Индексом
переменного
состава называют
отношение
двух
средних
уровней.
Индекс
фиксированного
состава есть
средний
из
индивидуальных
индексов.
Он
рассчитывается
как
отношение
двух
стандартизованных
средних,
где
влияние
изменения
структурного
фактора
устранено,
поэтому
данный
индекс
называют
еще
индексом
постоянного
состава.
В
зависимости
от
характера
и
содержания
индексируемых
величин
различают индексы
количественных (объемных) показателей и индексы
качественных
показателей.
10.2.
Индексы
количественных
показателей
К индексам
количественных
(объемных)
показателей относятся
такие
индексы,
как
индексы
физического
объема
производства
продукции,
затрат
на
выпуск
продукции,
стоимости
продукции,
а
также
индексы
показателей,
размеры
которых
определяются
абсолютными
величинами.
Используются
различные
виды
индексов
количественных
показателей.
Индекс
физического
объема
продукции (ФОП)
отражает
изменение
выпуска
продукции.
Индивидуальный
индекс
ФОП
отражает
изменение
выпуска
продукции
одного
вида
и
определяется
по
формуле
(10.1)
где
q1 и
q0 —
количество
продукции
данного
вида
в
натуральном
выражении
в
текущем
и
базисном
периодах.
Агрегатный
индекс ФОП
(предложен Э.
Ласпейресом)
отражает
изменение
выпуска
всей
совокупности
продукции,
где
индексируемой
величиной
является
количество
продукции
q, а
соизмерителем
— цена
р:

где
q1 и
q0 —
количество
выработанных
единиц
отдельных
видов
продукции
соответственно
в
отчетном
и
базисном
периодах;
p0 —
цена
единицы
продукции
(отдельного
вида)
в
базисном
периоде.
При
вычислении
индекса
ФОП
в
качестве
соизмерителей
может
выступать
также
себестоимость
продукции
или
трудоемкость.
Средние
взвешенные
индексы
ФОП
используются
в
том
случае,
если
известны
индивидуальные
индексы
объема
по
отдельным
видам
продукции
и
стоимость
отдельных
видов
продукции
(или
затраты)
в
базисном
или
отчетном
периоде.
Средний
взвешенный
арифметический
индекс ФОП
определяется
по
формуле

где
iq —
индивидуальный
индекс
по
каждому
виду
продукции;
q0 p0 —
стоимость
продукции
каждого
вида
в
базисном
периоде.
Средний
взвешенный
гармонический
индекс ФОП
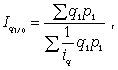
где
q1 p1 —
стоимость
продукции
каждого
вида
в
текущем
периоде.
Аналогично
рассчитывается индекс
затрат
на
выпуск
продукции (ЗВП),
который
отражает
изменение
затрат
на
производство
и
может
быть
как
индивидуальным,
так
и
агрегатным.
Индивидуальный
индекс ЗВП
отражает
изменение
затрат
на
производство
одного
вида
и
определяется
по
формуле

где
z1 и
z0 —
себестоимость
единицы
продукции
искомого
вида
в
текущем
и
базисном
периодах;
q1 z1 и
q0 z0 —
суммы
затрат
на
выпуск
продукции
искомого
вида
в
текущем
и
базисном
периодах.
Агрегатный
индекс ЗВП
характеризует
изменение
общей
суммы
затрат
на
выпуск
продукции
за
счет
изменения
количества
выработанной
продукции
и
ее
себестоимости
и
определяется
по
формуле
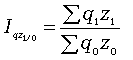
где
q1 z1 и
q0 z0 —
затраты
на
выпуск
продукции
каждого
вида
соответственно
в
отчетном
и
базисном
периодах.
Рассмотрим
построение индекса
стоимости
продукции
(СП),
который
может
определяться
и
как
индивидуальный,
и
как
агрегатный.
Индивидуальный
индекс СП
характеризует
изменение
стоимости
продукции
данного
вида
и
имеет
вид:

где
p1 и
p0 —
цена
единицы
продукции
данного
вида
в
текущем
и
базисном
периодах;
q1 p1 и
q0 p0 —
стоимость
продукции
данного
вида
в
текущем
и
базисном
периодах.
Агрегатный
индекс СП
(товарооборота)
характеризует
изменение
общей
стоимости
продукции
за
счет
изменения
количества
продукции
и
цен
и
определяется
по
формуле

10.3.
Индексы
качественных
показателей.
Факторный
анализ
Качественные
показатели
определяют
уровень
исследуемого
итогового
показателя
и
определяются
путем
соотношения
итогового
показателя
и
определенного
количественного
показателя
(например,
средняя
заработная
плата
определяется
путем
соотношения
фонда
заработной
платы
и
количества
работников).
К
индексам
качественных
показателей
относятся
индексы
цен,
себестоимости,
средней
заработной
платы,
производительности
труда.
Самым
распространенным
индексом
в
этой
группе
является
индекс
цен.
Индивидуальный
индекс
цен характеризует
изменение
цен
по
одному
виду
продукции
и
определяется
по
формуле

где
p1 и
p0 —
цена
за
единицу
продукции
в
текущем
и
базисном
периодах.
Соответственно
определяются
индексы
себестоимости
и
затрат
рабочего
времени
по
каждому
виду
продукции.
Агрегатный
индекс
цен определяет
среднее
изменение
цены
р
по
совокупности
определенных
видов
продукции
q.
Для
характеристики
среднего
изменения
цен
на
потребитель-ские
товары
используют
индекс
цен,
предложенный Э.
Ласпейресом
(индекс
Ласпейреса):

где
q0 —
потребительская
корзина
(базовый
период);
p0 и
p1 —
соответственно
цены
базисного
и
отчетного
периодов.
Если
количество
набора
продуктов
принимается
на
уровне
отчетного
периода
(q1 ),
то
в
этом
случае
индекс
цен
именуется индексом
Пааше:

Если
известны
индивидуальные
индексы
цен
по
отдельным
видам
продукции
и
стоимость
отдельных
видов
продукции,
то
применяются
средние
взвешенные
индексы
цен
(средний
взвешенный
арифметический
и
средний
взвешенный
гармонический
индексы
цен).
Формула среднего
взвешенного
арифметического
индекса
цен

где
i — индивидуальный
индекс
по
каждому
виду
продукции;
p0 q0 —
стоимость
продукции
каждого
вида
в
базисном
периоде.
Формула среднего
взвешенного
гармонического
индекса
цен
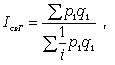
где
p1 q1 —
стоимость
продукции
каждого
вида
в
текущем
периоде.
В
статистической
практике
очень
широко
используется
агрегатный
территориальный
индекс
цен,
который
может
быть
рассчитан
по
следующей
формуле:
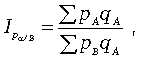
где
pA pB —
цена
за
единицу
продукции
каждого
вида
соответственно
на
территории
А
и
В;
qA —
количество
выработанной
или
реализованной
продукции
каждого
вида
по
территории
А
(в
натуральном
выражении).
Из
формулы
видно,
что
в
данном
индексе
в
качестве
фиксированного
показателя
(веса)
принят
объем
продукции
территории
А.
При
расчете
данного
индекса
в
качестве
веса
можно
принять
также
объем
продукции
территории
В
или
суммарный
объем
продукции
двух
территорий.
Возможны
два
способа
расчета
индексов:
цепной
и
базисный.
Цепные
индексы получают
путем
сопоставления
текущих
уровней
с
предшествующим,
при
этом
база
сравнения
постоянно
меняется.
Базисные
индексы получают
путем
сопоставления
с
тем
уровнем
периода,
который
был
принят
за
базу
сравнения.
В
качестве
примера
можно
привести
цепные
и
базисные
индексы
цен.
Цепные
индивидуальные
индексы
цен имеют
следующий
ряд
расчета:
…
. (10.15)
Базисные
индивидуальные
индексы
цен:
…
. (10.16)
Следует
помнить,
что
произведение
цепных
индивидуальных
индексов
цен
равно
последнему
базисному
индексу:
(10.17)
Цепные
агрегатные
индексы
цен:

. (10.18)
Базисные
агрегатные
индексы
цен:
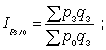
. (10.19)
Между
индексами
существует
также
взаимосвязь
и
взаимозависимость,
как
и
между
самими
экономическими
явлениями,
что
позволяет
проводить
факторный
анализ.
Благодаря
индексному
методу
можно
рассматривать
все
факторы
независимо
друг
от
друга,
что
дает
возможность
определить
размер
абсолютного
изменения
сложного
явления
за
счет
каждого
фактора
в
отдельности.
Предположим,
что
результативный
признак
зависит
от
трех
факторов
и
более.
В
этом
случае результативный
индекс примет
вид
(10.20)
Изменение
результативного
индекса
за
счет
каждого
фактора
может
быть
выражено
следующим
образом:

(10.21)
Для
выявления
роли
каждого
фактора
в
отдельности
индекс
сложного
показателя
разлагают
на
частные
(факторные)
индексы,
которые
характеризуют
роль
каждого
фактора.
При
этом
используют
два
метода:
-
метод
обособленного
изучения
факторов; -
последовательно-цепной
метод.
При
первом
методе
сложный
показатель
берется
с
учетом
изменения
лишь
того
фактора,
который
взят
в
качестве
исследуемого,
все
остальные
остаются
неизменными
на
уровне
базисного
периода.
Последовательно-цепной
метод
предполагает
использование
системы
взаимосвязанных
индексов,
которая
требует
определенного
расположения
факторов.
Как
правило,
на
первом
месте
в
цепи
располагают
качественный
фактор.
При
определении
влияния
первого
фактора
все
остальные
сохраняются
в
числителе
и
знаменателе
на
уровне
базисного
периода,
при
определении
второго
факторного
индекса
первый
фактор
сохраняется
на
уровне
базисного
периода,
а
третий
и
все
последующие
— на
уровне
отчетного
периода,
при
определении
третьего
факторного
индекса
первый
и
второй
факторы
сохраняются
на
уровне
базисного
периода,
четвертый
и
все
остальные
— на
уровне
отчетного
периода
и
т.д.
8.
Выборочное
наблюдение
относится
к
разновидности несплошного
наблюдения.
Оно
охватывает
отобранную
часть
единиц
генеральной
совокупности.
Цель
выборочного
наблюдения
— по
отобранной
части
единиц
дать
характеристику
всей
совокупности
единиц.
Чтобы
отобранная
часть
была
репрезентативна
(т.е.
представляла
всю
совокупность
единиц),
выборочное
наблюдение
должно
быть
специально
организовано.
Следовательно,
в
отличие
от
генеральной
совокупности,
представляющей
всю
совокупность
исследуемых
единиц,
выборочная
совокупность
представляет
ту
часть
единиц
генеральной
совокупности,
которая
является
объектом
непосредственного
наблюдения.
По
понятным
причинам
выборочный
метод
может
широко
использоваться
органами
государственной
статистики.
Он
позволяет
при
значительной
экономии
средств
и
затрат
получать
необходимую
достоверную
информацию.
Гарантия
репрезентативности
обеспечивается
применением
научно
обоснованных
способов
отбора
единиц,
которые
подлежат
обследованию.
Следует
сразу
же
иметь
в
виду,
что
при
сопоставлении
показателей
по
результатам
выборочного
исследования
с
характеристиками
для
всей
генеральной
совокупности
могут
иметь
место
отклонения.
Величина
этих
отклонений
называется
ошибкой
наблюдения,
которая
может
быть
или ошибкой
регистрации(несовершенство
технических
условий),
или ошибкой
репрезентативности (случайное
или
систематическое
нарушение
правил
при
отборе
единиц).
В
статистике
приняты
следующие
условные
обозначения:
N
— объем
генеральной
совокупности;
п
— объем
выборочной
совокупности;
—
средняя
в
генеральной
совокупности;
—
средняя
в
выборочной
совокупности;
р
— доля
единиц
в
генеральной
совокупности;
w
— доля
единиц
в
выборочной
совокупности;
—
генеральная
дисперсия;
S2 —
выборочная
дисперсия;
—
среднее
квадратическое
отклонение
признака
в
генеральной
совокупности;
S
— среднее
квадратическое
отклонение
признака
в
выборочной
совокупности.
11.2.
Виды
выборки,
способы
отбора
и
ошибки
выборочного
наблюдения
По
способу
отбора
(способу
формирования)
выборки
единиц
из
генеральной
совокупности
распространены
следующие
виды выборочного
наблюдения:
-
простая
случайная
выборка
(собственно-случайная); -
типическая
(стратифицированная); -
серийная
(гнездовая); -
механическая;
-
комбинированная;
-
ступенчатая.
Простая
случайная
выборка
(собственно—случайная) есть
отбор
единиц
из
генеральной
совокупности
путем
случайного
отбора,
но
при
условии
вероятности
выбора
любой
единицы
из
генеральной
совокупности.
Отбор
проводится
методом
жеребьевки
или
по
таблице
случайных
чисел.
Типическая
(стратифицированная)
выборка предполагает
разделение
неоднородной
генеральной
совокупности
на
типологические
или
районированные
группы
по
какому-либо
существенному
признаку,
после
чего
из
каждой
группы
производится
случайный
отбор
единиц.
Для серийной
(гнездовой)
выборки характерно
то,
что
генеральная
совокупность
первоначально
разбивается
на
определенные
равновеликие
или
неравновеликие
серии
(единицы
внутри
серий
связаны
по
определенному
признаку),
из
которых
путем
случайного
отбора
отбираются
серии
и
затем
внутри
отобранных
серий
проводится
сплошное
наблюдение.
Механическая
выборка представляет
собой
отбор
единиц
через
равные
промежутки
(по
алфавиту,
через
временные
промежутки,
по
пространственному
способу
и
т.д.).
При
проведении
механического
отбора
генеральная
совокупность
разбивается
на
равные
по
численности
группы,
из
которых
затем
отбирается
по
одной
единице.
Комбинированная
выборка основана
на
сочетании
нескольких
способов
выборки.
Многоступенчатая
выборка есть
образование
внутри
генеральной
совокупности
вначале
крупных
групп
единиц,
из
которых
образуются
группы,
меньшие
по
объему,
и
так
до
тех
пор,
пока
не
будут
отобраны
те
группы
или
отдельные
единицы,
которые
необходимо
исследовать.
Выборочный
отбор
может
быть
повторным
и
бесповторным.
При повторном
отборе вероятность
выбора
любой
единицы
не
ограничена.
При бесповторном
отборе выбранная
единица
в
исходную
совокупность
не
возвращается.
Для
отобранных
единиц
рассчитываются
обобщенные
показатели
(средние
или
относительные)
и
в
дальнейшем
результаты
выборочного
исследования
распространяются
на
всю
генеральную
совокупность.
Основной
задачей
при
выборочном
исследовании
является
определение
ошибок
выборки.
Принято
различать
среднюю
и
предельную
ошибки
выборки.
Для
иллюстрации
можно
предложить
расчет
ошибки
выборки
на
примере
простого
случайного
отбора.
Расчет средней
ошибки
повторной
простой
случайной
выборки производится
следующим
образом:
cредняя
ошибка
для
средней

cредняя
ошибка
для
доли

Расчет средней
ошибки
бесповторной
случайной
выборки:
средняя
ошибка
для
средней

средняя
ошибка
для
доли
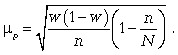
Расчет предельной
ошибки повторной
случайной
выборки:
предельная
ошибка
для
средней
предельная
ошибка
для
доли

где
t — коэффициент
кратности;
Расчет предельной
ошибки
бесповторной
случайной
выборки:
предельная
ошибка
для
средней

предельная
ошибка
для
доли

Следует
обратить
внимание
на
то,
что
под
знаком
радикала
в
формулах
при
бесповторном
отборе
появляется
множитель,
где
N — численность
генеральной
совокупности.
Что
касается
расчета
ошибки
выборки
в
других
видах
выборочного
отбора
(например,
типической
и
серийной),
то
необходимо
отметить
следующее.
Для типической
выборки величина
стандартной
ошибки
зависит
от
точности
определения
групповых
средних.
Так,
в
формуле
предельной
ошибки
типической
выборки
учитывается
средняя
из
групповых
дисперсий,
т.е.

При серийной
выборке величина
ошибки
выборки
зависит
не
от
числа
исследуемых
единиц,
а
от
числа
обследованных
серий
(s) и
от
величины
межгрупповой
дисперсии:
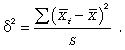
Серийная
выборка,
как
правило,
проводится
как
бесповторная,
и
формула
ошибки
выборки
в
этом
случае
имеет
вид
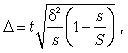
где -межсерийная
дисперсия;
s — число
отобранных
серий;
S — число
серий
в
генеральной
совокупности.
Все
вышеприведенные
формулы
применимы
для большой
выборки.
Кроме
большой
выборки
используются
так
называемые малые
выборки (n
< 30), которые
могут
иметь
место
в
случаях
нецелесообразности
использования
больших
выборок.
При
расчете
ошибок
малой
выборки
необходимо
учесть
два
момента:
1)
формула
средней
ошибки
имеет
вид

2)
при
определении
доверительных
интервалов
исследуемого
показателя
в
генеральной
совокупности
или
при
нахождении
вероятности
допуска
той
или
иной
ошибки
необходимо
использовать
таблицы
вероятности Стьюдента,
где
Р
= S (t, n), при
этом
Р
определяется
в
зависимости
от
объема
выборки
и
t.
В
статистических
исследованиях
с
помощью
формулы
предельной
ошибки
можно
решать
ряд
задач.
1.
Определять
возможные
пределы
нахождения
характеристики
генеральной
совокупности
на
основе
данных
выборки.
Доверительные
интервалы
для
генеральной
средней можно
установить
на
основе
соотношений
(11.12)
где
— генеральная
и
выборочная
средние
соответственно; -предельная
ошибка
выборочной
средней.
Доверительные
интервалы
для
генеральной
доли устанавливаются
на
основе
соотношений
(11.13)
2.
Определять
доверительную
вероятность,
которая
означает,
что
характеристика
генеральной
совокупности
отличается
от
выборочной
на
заданную
величину.
Доверительная
вероятность
является
функцией
от
t, где
(11.14)
Доверительная
вероятность
по
величине
t определяется
по
специальной
таблице.
3.
Определять
необходимый
объем
выборки
с
помощью
допустимой
величины
ошибки:
(11.15)
Чтобы
рассчитать
численность
п
повторной
и
бесповторной
простой
случайной
выборки,
можно
использовать
следующие
формулы:
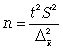
средней
при
повторном
способе);
(11.16)
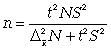
средней
при
бесповторном
способе);
(11.17)

доли
при
повторном
способе);
(11.18)

доли
при
бесповторном
способе).
(11.19)
9.
Методы многомерного статистическогоанализа
Методы математической статистики, используемые для построения оптимальных планов сбора,систематизации и обработки многомерных статистических данных, направленные на выявление характера иструктуры взаимосвязей между компонентами исследуемого многомерного признака и предназначенные дляполучения научных и практических выводов.
По содержанию Мм.с.а. могут быть условно разделены на три основные группы:
1) Мм.с.а. многомерных распределений и их основных характеристик;
2) Мм.с.а. характера и структуры взаимосвязей между компонентами исследуемого многомерногопризнака;
3) М.м.с.а. геометрической структуры исследуемой совокупности многомерных наблюдений.
Методы первой группы охватывают лишь те ситуации, в которых обрабатываемые наблюдения имеютвероятностную природу, т. е. интерпретируются как выборка из соответствующей генеральной совокупности.К основным задачам этого подраздела относятся: статистическое оценивание исследуемых многомерныхраспределений, их основных числовых характеристик и параметров, исследование распределениявероятностей для ряда статистик, с помощью которых строятся статистические критерии проверки различныхгипотез о вероятностной природе анализируемых многомерных данных. Вторая группа методов объединяет всебе понятия и результаты, обслуживающие такие методы и модели математического статистическогоанализа, как множественная регрессия, многомерный дисперсный анализ, факторный анализ и др.Результаты данных методов могут быть условно разделены на два основных типа: а) построение наилучшихстатистических оценок для параметров этих моделей и анализ их свойств (точности, а в вероятностнойпостановке — законов их распределения, доверительных областей и т. д.); б) построение статистическихкритериев для проверки различных гипотез о структуре исследуемых взаимосвязей. Третья группа -объединяет в себе понятия и результаты таких моделей и схем, как дискриминантный анализ, анализмногомерного шкалирования. Узловым во всех этих схемах является понятие расстояния (меры близости,меры сходства) между анализируемыми элементами. При этом анализируемыми могут быть как реальныеобъекты, так и сами показатели.
Прикладное назначение М. м. с.а. состоит в основном в обслуживании трех проблем:
1) проблема статистического исследования зависимостей между анализируемыми показателями;
2) проблема классификации элементов (объектов или показателей) в общей (нестрогой) постановке, чтобывсю анализируемую совокупность элементов, статистически представленную в виде матрицы, разбить насравнительно небольшое число однородных групп;
3) проблема снижения размерности исследуемого факторного пространства и отбора наиболееинформативных показателей.
♦ методы анализа социолингвистических исследований
Среднегодовое увеличение стоимости инвестиционного актива, портфеля или денежного потока называется среднегодовой темп роста.
Что такое среднегодовой темп роста?
Среднегодовой темп роста — это среднегодовое увеличение стоимости инвестиционного актива, портфеля или денежного потока. Он определяется путем взятия среднего численного значения заданных или рассчитанных годовых темпов роста.
Среднегодовой темп роста используется во многих областях — например, в экономике, где он дает четкое представление о сдвигах в экономических показателях (например, фактический темп роста ВВП).
Среднегодовой темп роста обычно представляется в процентах.
Резюме
- Среднегодовой темп роста — это среднее увеличение или уменьшение стоимости инвестиционного актива, портфеля или денежного потока за определенный период времени.
- Он определяется путем взятия среднего значения определенных годовых темпов роста.
- Среднегодовой темп роста можно рассчитать для любой инвестиции. Однако он не дает представления о потенциальном риске инвестиции, определяемом колебаниями ее цены.
Использование среднегодового темпа роста
Показатель среднегодового темпа роста полезен для оценки долгосрочных тенденций. Он имеет отношение практически к любой форме анализа финансовых показателей, таких как темпы роста прибыли, продаж, денежных потоков, расходов и т.д., чтобы дать инвесторам представление о направлении, в котором движется фирма. Среднегодовой темп роста показывает, какова в среднем была годовая доходность.
Формула среднегодового темпа роста
Среднегодовой темп роста = [(Темп роста)y + (Темп роста)y+1 + … (Темп роста)y+n] / N
Где:
- Темп роста (y) — темп роста в первый год;
- Темп роста (y + 1) — темп роста в следующем году;
- Темп роста (y + n) — темп роста в году «n»;
- N — общее количество периодов.
Как рассчитывается среднегодовой темп роста
Среднегодовой темп роста — это эталон для расчета средней доходности инвестиций за ряд лет. По сути, это базовый средний темп роста доходности для последовательности периодов (лет).
Чтобы рассчитать среднее значение, необходимо рассчитать темпы роста для каждого отдельного временного периода в серии. Это можно сделать с помощью приведенной ниже базовой формулы:
Процент роста = ((EV / BV) — 1) x 100%
Где:
- EV — конечное значение;
- BV — начальное значение.
После расчета процентов темпов роста для каждого временного периода они суммируются и делятся на общее количество временных периодов, в результате чего получается среднегодовой темп роста.
При расчете темпов роста всегда следует учитывать, что используемые периоды должны быть одинаковыми по продолжительности. Эти временные периоды могут быть годовыми, месячными, квартальными и т.д., в зависимости от конкретных потребностей человека или фирмы, рассчитывающих темпы роста.
Пошаговый пример
Учитывая следующие годовые доходы компании ABC:
Год 1: $250,000;
Год 2: $356 000;
Год 3: $390 000;
Год 4: $395 000;
Год 5: $400,000;
Год 6: $358,000;
Год 7: $320 000.
Используя приведенную выше формулу темпов роста, темпы роста с 1-го по 7-й год можно рассчитать следующим образом:
Y1: 0, поскольку нет предшествующего периода времени;
Y2: [(356,000/250,000)-1] x 100% = 42.4%;
Y3: [(390,000/356,000)-1] x 100% = 9.7%;
Y4: [(395,000/390,000)-1] x 100% = 101.3%;
Y5: [(400,000/395,000)-1] x 100% = 101.3%;
Y6: [(358,000/400,000)-1] x 100% = -10.5%;
Y7: [(320,000/358,000)-1] x 100% = -10.6%.
А среднегодовой темп роста рассчитывается следующим образом:
Сумма темпов роста = [42,4 % + 9,7 % + 101,3 % + 101,3 % + (-10,5 %) + (-10,6 %)]
= 233.6%
Среднегодовой темп роста = 233,6 % / 7
= 33.4%;
Среднегодовой темп роста для компании ABC составляет 33,4%.
Среднегодовой темп роста Ограничения в финансовом анализе
Рассмотрим портфель, который растет на 25% в первый год и на 12% в последующие. Среднегодовой темп роста будет рассчитан как 18,5%. Колебания в доходности портфеля между началом первого года и концом года не учитываются при расчете среднегодового темпа роста.
Это может привести к определенным ошибкам в оценке. Поскольку среднегодовой темп роста является средним значением годовой доходности, эта метрика не дает оценки общего риска, связанного с инвестицией, который оценивается по нестабильности ее цены. В принципе, среднегодовой темп роста может быть рассчитан для любой инвестиции, однако он не дает никакого представления о потенциальном риске инвестиций.
Кроме того, среднегодовой темп роста не учитывает эффект компаундирования, поскольку является линейной метрикой. Анализ может показать, что инвестиции росли в среднем на n процентов в год, но при этом упустить колебания, которые могли произойти в течение временного периода.
Идеально подходящий для демонстрации тенденций, среднегодовой темп роста также может быть обманчивым для инвесторов, поскольку он неадекватно отражает меняющиеся финансовые тенденции. Кроме того, рост инвестиций может быть переоценен.
Дополнительные ресурсы:
Спасибо, что ознакомились с руководством Finansistem по среднегодовому темпу роста. Чтобы продолжать учиться и продвигаться по карьерной лестнице, вам будут полезны дополнительные ресурсы Finansistem, представленные ниже:
- Управление активами и пассивами (ALM)
- Лестничный портфель облигаций
- Номинальная норма прибыли
- Инвестиционный портфель













