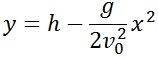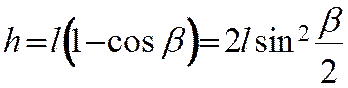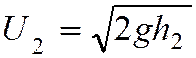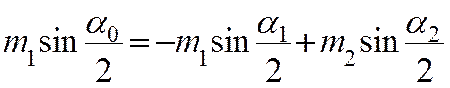Цель работы: проверить закон независимости движений на примере движения тела, брошенного горизонтально.
Оборудование: небольшой шарик, желоб, линейка, секундомер, указка, лист бумаги и копировальная бумага, (ящик с песком).
Порядок выполнения работы:
1. Соберите установку, изображенную на рисунке. Нижний участок желоба должен быть горизонтальным, а расстояние h от нижнего края желоба до стола должно быть равным примерно 40 см. Лапки зажима должны быть расположены вблизи верхнего конца желоба.
2. Положите под желобом лист бумаги, придавив его книгой, чтобы он не сдвигался при проведении опытов. Отметьте на этом листе с помощью отвеса точку А, находящуюся на одной вертикали с нижним концом желоба.
3. Поместите в желоб шарик так, чтобы он касался зажима, и отпустите шарик без толчка. Заметьте (примерно) место на столе, куда попадает шарик, скатившись с желоба и пролетев по воздуху. На отмеченное место положите лист бумаги, а на него — лист копировальной бумаги «рабочей» стороной вниз. Придавите эти листы книгой, чтобы они не сдвигались при проведении опытов.
4. Снова поместите в желоб шарик так, чтобы он касался зажима, и отпустите без толчка. Измерьте время падения шарика. Повторите этот опыт 5 раз, следя за тем, чтобы лист копировальной бумаги и находящийся под ним лист не сдвигались.
5. Осторожно снимите лист копировальной бумаги, не сдвигая находящегося под ним листа, и отметьте точки, лежащие между отпечатками. Учтите при этом, что видимых отпечатков может оказаться меньше 5-ти, потому что некоторые отпечатки могут слиться.
6. Измерьте расстояние li от отмеченных точек до точки А.
7. Результаты измерений запишите в таблицу 1:
Таблица № 1
|
№ опыта |
h, м |
t1, c |
tср, c |
|
li, м |
|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 |
8. Рассчитайте среднее время падения шарика:
tср=(t1+t2+t3+t4+t5)/5
9. Зная высоту h, с которой падал шарик и ускорение свободного падения g=9,8 м/с2, вычислите время движения шарика:
10. Сравните рассчитанное значение со средним временем падения шарика, определенным из опыта. Сделайте вывод.
11. Определите начальную скорость шарика для каждого из измеренных значений дальности полета:
12. Результаты вычислений занесите в таблицу 1.
13. Выбрав правильный масштаб по осям OX и OY и воспользовавшись уравнением траектории:
постройте траекторию движения шарика для одного из найденных значений начальной скорости.
14. Сделайте вывод по проделанной работе.
Пример выполнения работы:
Опыт:
Таблица № 1 Результат измерений.
|
№ опыта |
h, м |
t1, c |
tср, c |
|
li, м |
|
| 1 | 0,41 | 0,32 | 0,41 | |||
| 2 | 0,38 | 0,426 | ||||
| 3 | 0,26 | 0,435 | ||||
| 4 | 0,24 | 0,426 | ||||
| 5 | 0,31 | 0,444 |
Для оформления работы можно воспользоваться примером: Решение к лабораторной работе «Изучение движения тела, брошенного горизонтально» (для вычислений и построения таблицы воспользоваться своими данными)
Вообще-то матемтический маятник совершает колебательные движения, близкие к гармоническим
И его редняя скорость РАВНА НУЛЮ
Просто потому, что жди хоть 10000 лет у качающегося маятника — с места он не сдвинется
Впрочем может нужна средняя величина модуля скорости?
Тогда уравнение движения 
Период маятника равен 2пиКОРЕНЬ (L/g), L = 30-40 см
полпериода очевидно пи2пиКОРЕНЬ (L/g) — это время
Амплитула дана в градусах, длину дуги можно приближённо считать длиной катета, A=LCOS(20-30)
Путь за полпериода равен удвоенной амплитуде очевидно
Осталось разделить одно на другое
где t — время
в течении которого на тело действовала сила F,
изменившая импульс тела на величину DR.
Применительно к удару в уравнении (14) F – средняя сила удара,
t — время
удара, т.е. время соприкосновения ударяющихся тел, DR=DmV, где m – масса одного из соударяющихся тел (второе тело
неподвижно), DV – изменение скорости этого тела, возникающее в результате
удара. Если бьющий шар после удара остается в покое, то DV=V, где V – скорость шара в
момент удара которая, согласно (10) равна
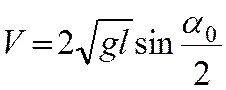
Подставив (15) в (14) получаем окончательное выражение для
средней силы упругого удара
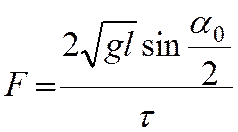
ВЫПОЛНЕНИЕ
УПРАЖНЕНИЯ.
1. Поместить на
нити подвеса шары одинаковой массы и отрегулировать их положение.
2. Измерить время t соударения шаров не менее 10 раз.
Результаты занести в таблицу 2 и обработать.
3. Определив длину
подвеса, массу одного шара и значение угла по
формуле (16), рассчитать среднюю силу удара.
Упражнение 3: проверка закона сохранения импульса и
определение энергии остаточной деформации при неупругом ударе.
Законы сохранения импульса и энергии при неупругом
ударе имеют вид
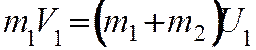
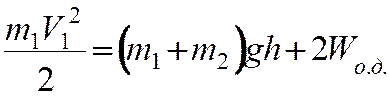
где — масса бьющего
пластилинового шара,
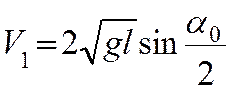
— масса ударяемого
шара,
— максимальная высота
подъема двух шаров после удара,
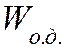
деформации.
Учитывая, что
и принимая во внимание выражение (10), вместо (17) и (16)
запишем рабочие формулы
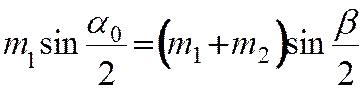
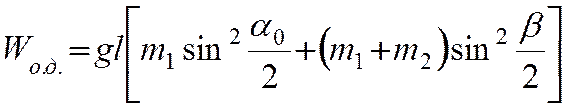
где b —
угол отклонения шаров после удара.
Упражнение выполняется для одного удара на
пластилиновых шарах. Порядок выполнения такой же, как и в упражнении 1. Опыт
проделать не менее 5 раз.
Упражнение №1
Проверка закона сохранения импульса и определение
коэффициента восстановления упругого удара.
=150
Таблица №1
|
№ |
|
|
|
1 |
0,25 |
8,5 |
|
2 |
0,1 |
9 |
|
3 |
0,25 |
8 |
|
4 |
0,25 |
8 |
|
5 |
0,2 |
8,25 |
|
6 |
0,3 |
8,5 |
|
7 |
0,2 |
9 |
|
8 |
0,25 |
8,5 |
|
9 |
0,15 |
9 |
|
10 |
0,15 |
8,5 |
|
|
0,28 |
8,7 |
|
|
62,255 |
7,507 |
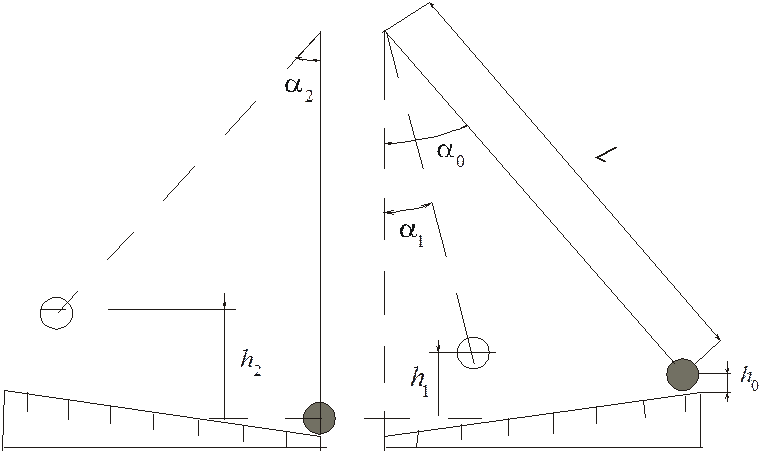 |
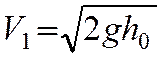
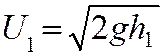
—
высота начального положения ударяющего (правого) шара (рис.2);
—
высота, на которую поднимается ударяющий (правый) шар после соударения;
—
высота, на которую поднимается ударяемый (левый) шар после соударения.
—
скорость правого шара в момент удара;
и
— скорости шаров после удара.
1|
2|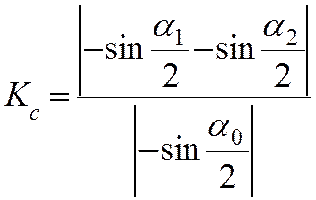
3|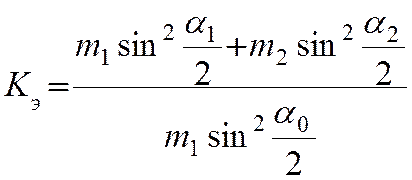
1| 0,106*0.938=
–0.106*0,1395+ 0.172*0.935
0.099=0.14
2|Кс=|-0,1395+0.935|/|-0.938|=0.848
3|Кэ=(0,106*0,01946025+0,172*0,874225)/(0,106*0,879844)=1,634
Вывод:
проверил закон
сохранения импульса и определил коэффициент восстановления упругого удара
Упражнение 2:определение времени упругого удара и
средней силы соударения шаров.
Таблица №2
|
№ |
t |
|
1 |
69 |
|
2 |
77 |
|
3 |
75 |
|
4 |
79 |
|
5 |
78 |
|
6 |
72 |
|
7 |
75 |
|
8 |
74 |
|
9 |
78 |
|
10 |
76 |
|
tср |
75 |
l = 47 см = 0.47 см
1)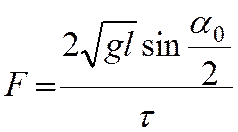
Н.
Вывод:
определил время
упругого удара и среднюю силу соударения шаров.
КОНТРОЛЬНЫЕ
ВОПРОСЫ.
1. Внутренние и
внешние силы.
2. Импульс. Закон
сохранения импульса (доказать).
3. Типы удара
твердых тел.
4. Количественные
характеристики удара твердых тел.
5. Как изменяются
кинетическая энергия шаров и их относительная скорость при различных видах
удара: абсолютно упругом, неупругом и абсолютно неупругом (доказать).
6. Вывести рабочие
формулы.
ЛИТЕРАТУРА
1.
Сивухин Д.В. Общий курс физики. т.1, §§10-12,
18, 26, 28, М., 1979.
2.
Матвеев А.Н. Механика и теория относительности, М., 1976.
3.
Петровский И.И. Механика, Минск, 1973, гл.VI,
§§10-12.
4.
Савельев И.В. Курс общей физика, т.1, §§22, 23, 30.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
2.1
Расчет скорости шарика до удара.
Формула
:
1=2*Sin(
i
/
2)*g*L
L
– Длинна
нити.
g
– Скорость свободного падения.
1
–
Скорость
шарика до удара.
I
– Угол
отклонения шарика.
2.2
Расчет скорости шарика после удара.
Формула
:
2=2*Sin(<
i>
/
2)*g*L
<i>
— Среднее
значение угла отскока шарика.
Производим
вычисления :
1
= 2*Sin(200/2)*9,81*0,315
= 0,605 (м/с).
2= 2*Sin(17.50/2)*
9,81*0,315
= 0,532 (м/с).
1
= 2*Sin(300/2)*9,81*0,315
= 0,905 (м/с).
2
= 2*Sin(26.50/2)*9,81*0,315
= 0,802 (м/с).
1
= 2*Sin(400/2)*9,81*0,315
= 1,197 (м/с).
2
= 2*Sin(35.50/2)*9,81*0,315
= 1,067 (м/с).
1= 2*Sin(500/2)*
9,81*0,315
= 1,479 (м/с).
2
= 2*Sin(430/2)*9,81*0,315
= 1,282 (м/с).
1
= 2*Sin(600/2)*9,81*0,315
= 1,757 (м/с).
2
= 2*Sin(500/2)*9,81*0,315
= 1,479 (м/с).
Результаты расчетов
сведем в таблицу
Таблица
5
|
|
|
|
|
|
|
|
|
0,605 |
0,905 |
1,197 |
1,479 |
1,757 |
|
|
0,532 |
0,802 |
1,067 |
1,282 |
1,479 |
3. Расчет среднего значения силы удара
Формула
:
<
F >
=
<F>
— Среднее
значение силы удара.
m – Масса
шарика.
1
—
скорость
шарика до удара.
2
— скорость
шарика после удара.
–время удара.
Производим
вычисления :
<F1>
= 0,0195*(0,605-0,532)
/
0,0000309 = 46,06 H.
<F2>
= 0,0195*(0,905-0,802)
/ 0,0000287 = 69,98 H.
<F3>
= 0,0195*(1,197-1,067)
/ 0,0000269 = 94,23 H.
<F4>
= 0,0195*(1,479-1,282)
/ 0,0000217 = 177,02 H.
<F5>
= 0,0195*(1,757-1,479)
/ 0,0000191 = 283,82 H.
4. Расчет коэффициента восстановления.
Формула
:
ε
=
2
/
1
ε
— коэффициент восстановления.
ε
1 = 0,532 / 0,605
= 0,878 ε
5 = 1,479 / 1,757
= 1,187
ε
2 = 0,802 / 0,905
= 0,886
ε
3 = 1,067
/ 1,197 = 0,891
ε
4 = 1,282 / 1,479
= 0,866
5.Расчет погрешностей прямых измерений.
5.1
Определяем стандартную погрешность
измерения угла отскока шарика.
Формула
:
SI
=
(
S/I
)2
+
(
S//2
)2.
SI
— среднеквадратичное
отклонение.
S/I
— стандартная
случайная погрешность.
S//2
= 0, 5 — стандартная
систематическая погрешность.
S/I
=
∑(
I
—
<i>)2
/
N
( N
— 1 )
N=10
количество
измерений угла.
S/1=
(180-17.50)2+(17.50-17.50)2+(170-17.50)2+(180-17.50)2+(18.50-17.50)2+(170-17.50
)2
+(17.50-17.50)2+(170-17.50)2+(180-17.50)2+(180-17.50)2
/ 10( 10-1) = 0,176;
S=
(0,
5)2+(0,176)2
= 0,530;
S/2=
(270-26.50)2+(27.50+26.50)2+(260-26.50)2+(26.50-26.50)2+(270-26.50)2+(
270-26.50)2+(26.50-26.50)2+(
270-26.50)2+(
26.50-26.50)2+(
26.50-26.50)2
/ 10( 10-1) = 0,148;
S=
(0,
5)2+(0,148)2
= 0,521;
S/3=
(350-35.50)2+(35.50-35.50)2+(35.50-35.50)2+(360-35.50)2+(
35.50-35.50)2+(35.50-35.50)2+(
350-35.50)2+
(350-35.50)2+(
350-35.50)2+(
35.50-35.50)2
/ 10( 10-1) = 0,104
S=
(0,
5)2+(0,104)2
= 0,510;
S/4=
(43-43)2+(43-43)2+(43.5-43)2+(42-43)2+
(43-43)2+(
43.5-43)2+(
42.5-43)2+
(43-43)+ (43-43)2
+( 42.5-43) / 10( 10-1) = 0,139
S=
(0,
5)2+(0,139)2
= 0,518;
S/5=
(500-500)2+(500.5-500)2+
(500-500)2+(50.50-500)2+
(50.50-500)2+
(50.50-500)2+
(510-500)2+
(500-500)2+(49.50-500)2+
(50.50-500)2
/ 10( 10-1) = 0,158;
S=
(0,
5)2+(0,158)2
= 0,524
5.2
Расчет абсолютной погрешности угла
отклонения шарика
∆i
Формула
:
∆i
=
(kn
*
S/i)2+(1/3*k*S//
2
)2
kn
= 2.3 — соответствующий
коэффициент Стьюдента;
k
=
2.0
— соответствующий
коэффициент Стьюдента;
Производим
вычисления :
∆1=
(2.3*0,176)2+
(1/3*2.0*0, 5)2=
0,524
∆2=
(2.3*0,148)2+
(1/3*2.0*0, 5)2=
0,476
∆3=
(2.3*0,104)2+
(1/3*2.0*0, 5)2=
0,410
∆4=
(2.3*0,139)2+
(1/3*2.0*0, 5)2=
0,461
∆5=
(2.3*0,158)2+
(1/3*2.0*0, 5)2=
0,493
5.2
Определяем относительную погрешность
измерения угла отскока шарика.
Формула
:
εi=
∆I
/
<i>
ε1
=
0,524
/
17,50
= 0,029;
ε2
=
0,476
/
26,50
= 0,016;
ε3
=
0,410
/
35,50
= 0,012;
ε4
= 0,461
/ 43,00
= 0,011;
ε5
= 0,493
/ 50,00
=
0,010;
5.3
Определяем относительную и абсолютную
погрешность измерения угла отклонения
шарика .
Формулы
:
∆i
=
(kn
*
S/i)2+(1/3*k*S//
2
)2
ε
i=
∆I
/
<i>
т.к.
(kn
*
S/i)2
=
0
, то
∆i
=
(1/3*k*S//
2
)2.
Производим
вычисления :
∆I
=(1/3*2.0*0.5)2
= 0,33
ε1
=
0,33/20
= 0,016;
ε2
=
0,33/30
= 0,011;
ε3
=
0,33/40
= 0,008;
ε4
=
0,33/50
= 0,007;
ε5
=
0,33/60 = 0,006;
5.4
Рассчитаем относительную погрешность
измерения времени соударения шарика.
Формула
:
SI
=
∑(
i—
<i>)2
/
N ( N — 1 )
Производим
вычисления
:
S1=10-7*
(321-309)2+(312-309)2+(304-309)2+(312-309)2+(303-309)2+(307-309)2+(315-309)2+(309-309)2+(302-309)2+(311+309)2
/ 10( 10-1) =1,8*10-7
S2=10-7*
(272-287)2+(288-287)2+(271-287)2+(297-287)2+(287-287)2+(301-279)2+(286-287)2
+(291-287)2+(300-287)2
+(279-287)2
/ 10( 10-1) =3,37*10-7
S3=10-7*
(262-269)2+(267-269)2+(269-269)2+(262-269)2+(258-269)2+(252-269)2+(261-269)2
+(243-269)2+(255-269)2+
(261-269)2
/ 10( 10-1) = 4,10*10-7
S4=10-7*
(217+217)2+(216-217)2+(208-217)2+(212-217)2+(206-217)2+(231-217)2+(214-
-217)2+
(227-217)2+(221-217)2+(211-217)2
/ 10( 10-1) = 2,71*10-7
S5=10-7*
(
191-191)2+(189-191)2+(192-191)2+(184-191)2+(190-191)2+(183-191)2+(202-
191)2+
(193-191)2+(201-191)2+(186-191)2
/ 10( 10-1) = 2,27*10-7
5.5
Определим абсолютную погрешность
измерения времени соударения шарика.
Формула
:
∆I
=
(kn*S
)2+(1/3*k*
S/)2
S
—
стандартная
случайная погрешность.
S/
=1*10-7
—
стандартная
систематическая погрешность.
Производим
вычисления :
∆1
=
10-7*(2,3*1,8)2+(1/3*2,0*1)2
= 4,14*10-7;
∆2
=
10-7*(2,3*3,37)2+(1/3*2,0*1)2
= 7,75*10-7;
∆3
=
10-7*(2,3*4,10)2+(1/3*2,0*1)2
= 9,43*10-7;
∆4
=
10-7*(2,3*2,71)2+(1/3*2,0*1)2
= 6,23*10-7;
∆5
=
10-7*(2,3*2,27)2+(1/3*2,0*1)2
= 2,28*10-7;
5.6
Определим относительную погрешность
измерения времени соударения шарика.
Формула
:
ε=
∆I
/
<i>
ε1=
4,
14*10-7
/ 309 * 10-7
= 0,013;
ε2=
7,
75*10-7
/ 287* 10-7
= 0,027;
ε3=
9,
43*10-7
/ 269 *10-7
= 0,035;
ε4=
6,
23*10-7
/ 217* 10-7
= 0,028;
ε5=
2,
28*10-7
/ 191* 10-7
= 0,012;
Соседние файлы в папке Отчёты 1 семестр
- #
- #
28.03.2015126.98 Кб47маятник максвела(1).doc
- #
- #
- #
28.03.2015560.13 Кб44Мех. удар(1).doc
- #
- #
- #
28.03.2015891.39 Кб43Мех.удар(1).doc
- #
- #
- #
Определите время падения шарика и монеты с высоты 1 м и 2 м.
Определите время падения шарика и монеты с высоты 1 м и 2 м. Проведите по три измерения времени падения с каждой высоты и определите среднее время
Для проведения опыта нужны измерительные инструменты.
1) рулетка длиной 2 метра.
2) секундомер.
С рулеткой проблем нет, а с секундомером проблема решилась путем установки на Android смартфон приложения «секундомер-таймер» из Google Play Market. Секундомер там отличный, с тысячными долями секунды, то есть с миллисекундами.
Далее я соорудил испытательный стенд: на край стола высотой 70 см поставил колонку от компьютера и еще добавил книгами, чтобы получилось ровно 1 метр.
А вот для стенда высотой 2 метра я использовал настенную полку в комбинации с книгами.
Одновременно бросать и включать секундомер очень неудобно, получалась дурня. Попросил брата тыкать секундомер, а я сбрасывал. Вот получилось так:
Бросаем монету с высоты 1 метр.
1) t=0,531 c; 2) t=0,489 c; 3) t=0,544 c
Среднее время: $t_c=frac{t_1+t_2+t_3}{3}= frac{0,531+0,489+0,544}{3}approx 0,521;c$
Бросаем металлический шарик от велосипедного подшипника с высоты 1 метр.
1) t=0,523 c; 2) t=0,476 c; 3) t=0,567 c;
Среднее время: $t_c=frac{t_1+t_2+t_3}{3}= frac{0,523+0,476+0,567}{3}= 0,522;c$
Бросаем монету с высоты 2 метра.
1) t=0,698 c; 2) t=0,654 c; 3) t=0,673 c
Среднее время: $t_c=frac{t_1+t_2+t_3}{3}= frac{0,698+0,654+0,673}{3}approx 0,675;c$
Бросаем металлический шарик от велосипедного подшипника с высоты 2 метра.
1) t=0,703 c; 2) t=0,623c; 3) t=0,684 c;
Среднее время: $t_c=frac{t_1+t_2+t_3}{3}= frac{0,703+0,623+0,684}{3}= 0,67;c$

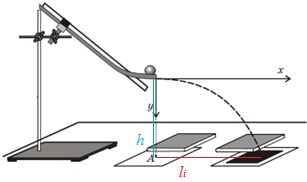
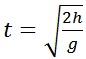 , с
, с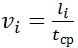 , с
, с