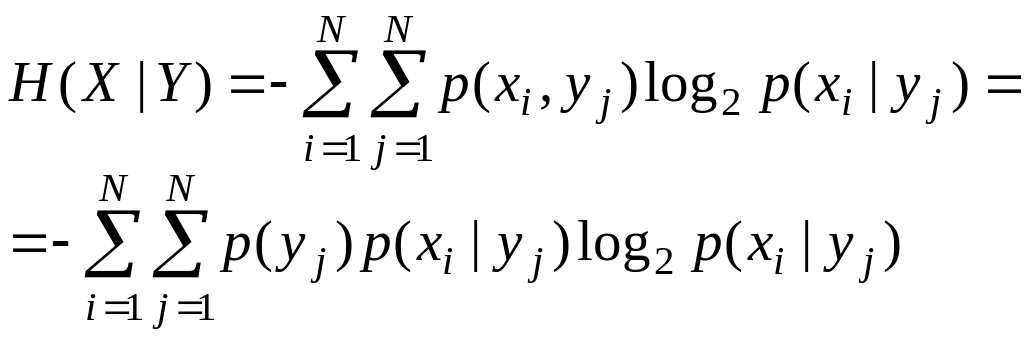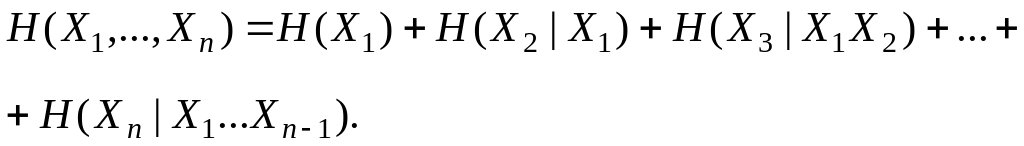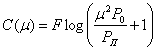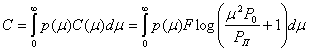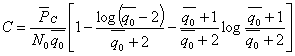Как найти среднее количество информации - Avtoru.top

Мы ежедневно работаем с информацией из разных источников. При этом каждый из нас имеет некоторые интуитивные представления о том, что означает, что один источник является для нас более информативным, чем другой. Однако далеко не всегда понятно, как это правильно определить формально. Не всегда большое количество текста означает большое количество информации. Например, среди СМИ распространена практика, когда короткое сообщение из ленты информационного агентства переписывают в большую новость, но при этом не добавляют никакой «новой информации». Или другой пример: рассмотрим текстовый файл с романом Л.Н. Толстого «Война и мир» в кодировке UTF-8. Его размер — 3.2 Мб. Сколько информации содержится в этом файле? Изменится ли это количество, если файл перекодировать в другую кодировку? А если заархивировать? Сколько информации вы получите, если прочитаете этот файл? А если прочитаете его второй раз?

По мотивам открытой лекции для Computer Science центра рассказываю о том, как можно математически подойти к определению понятия «количество информации».

В классической статье А.Н. Колмогорова «Три подхода к определению понятия количества информации» (1965) рассматривают три способа это сделать:

комбинаторный (информация по Хартли),
вероятностный (энтропия Шеннона),
алгоритмический (колмогоровская сложность).

Мы будем следовать этому плану.

Комбинаторный подход: информация по Хартли

Мы начнём самого простого и естественного подхода, предложенного Хартли в 1928 году.

Пусть задано некоторое конечное множество . Количеством информации в будем называть .

Можно интерпретировать это определение следующим образом: нам нужно chi(A) битов для описания элемента из .

Почему мы используем биты? Можно использовать и другие единицы измерения, например, триты или байты, но тогда нужно изменить основание логарифма на 3 или 256, соответственно. В дальшейшем все логарифмы будут по основанию 2.

Этого определения уже достаточно для того, чтобы измерить количество информации в некотором сообщении. Пусть про xin A стало известно, что xin B . Теперь нам достаточно битов для описания , таким образом нам сообщили битов информации.

Пример

Загадано целое число от до . Нам сообщили, что делится на . Сколько информации нам сообщили?

Воспользуемся рассуждением выше.

$log_2 1000 - log_2 166 = log_2 frac{1000}{166} approx 2.59 text{битов.}$

(Тот факт, что некоторое сообщение может содержать нецелое количество битов, может показаться немного неожиданным.)

Можно ещё сказать, что сообщение, уменшающее пространство поиска в alpha раз приносит битов информации. В данном примере пространство поиска уменьшилось в 1000/166 раз.

Интересно, что одного этого определения уже достаточно для того, чтобы решать довольно нетривиальные задачи.

Применение: цена информации

Загадано целое число от до . Разрешается задавать любые вопросы на ДА/НЕТ. Если ответ на вопрос «ДА», то мы должны заплатить рубль, если ответ «НЕТ» — два рубля. Сколько нужно заплатить для отгадывания числа ?

Любой вопрос можно сформулировать как вопрос о принадлежности некоторому множеству, поэтому мы будем считать, что все вопросы имеют вид « xin T ?» для некоторого множества .

Каким образом нужно задавать вопросы? Нам бы хотелось, чтобы вне зависимости от ответа цена за бит информации была постоянной. Другими словами, в случае ответа «НЕТ» и заплатив два рубля мы должны узнать в два больше информации, чем при ответе «ДА». Давайте запишем это формально.

Потребуем, чтобы

Пусть , тогда . Подставляем и получаем, что

Это эквивалентно квадратному уравнению Положительный корень этого уравнения . Таким образом, при любом ответе мы заплатим рублей за бит информации, а в сумме мы заплатим примерно clog n рублей (с точностью до округления).

Осталось понять, как выбирать такие множества . Будем выбирать в качестве непрерывные отрезки прямой. Пусть нам известно, что принадлежит отрезку [a,b] (изначально это отрезок [1,n] ). В следующего множества возмём отрезок , где. Тогда за каждый заплаченный рубль текущий отрезок будет уменьшаться в раз. Когда длина отрезка станет меньше единицы, мы однозначно определим . Поэтому цена отгадывания не будет превосходить

Приведённое рассуждение доказывает только верхнюю оценку. Можно доказать и нижнюю оценку: для любого способа задавать вопросы будет такое число , для отгадывания которого придётся заплатить не менее рублей.

Вероятностный подход: энтропия Шеннона

Вероятностный подход, предложенный Клодом Шенноном в 1948 году, обобщает определение Хартли на случай, когда не все элементы множества являются равнозначными. Вместо множества в этом подходе мы будем рассматривать вероятностное распределение на множестве и оценивать среднее по распределению количество информации, которое содержит случайная величина.

Пусть задана случайная величина , принимающая различных значений с вероятностями . Энтропия Шеннона случайной величины определяется как

$H(X) = sum_{i=1}^k p_icdotlogfrac1p_i.$

(По непрерывности тут нужно доопределить $0cdot logfrac10 = 0$ .)

Энтропия Шеннона оценивает среднее количество информации (математическое ожидание), которое содержится в значениях случайной величины.

При первом взгляде на это определение, может показаться совершенно непонятно откуда оно берётся. Шеннон подошёл к этой задаче чисто математически: сформулировал требования к функции и доказал, что это единственная функция, удовлетворяющая сформулированным требованиям.

Я попробую объяснить происхождение этой формулы как обобщение информации по Хартли. Нам бы хотелось, чтобы это определение согласовывалось с определением Хартли, т.е. должны выполняться следующие «граничные условия»:

Будем искать в виде математического ожидания количества информации, которую мы получаем от каждого возможного значения .

$H(X) = sum_i p_icdot text{(информация в событии $X=a_i$)}.$

Как оценить, сколько информации содержится в событии X = a_i ? Пусть — всё пространство элементарных исходов. Тогда событие X = a_i соответствует множеству элементарных исходов меры p_i . Если произошло событие X = a_i , то размер множества согласованных с этим событием элементарных исходов уменьшается с |U| до , т.е. событие X = a_i сообщает нам битов информации. Тут мы пользуемся тем, что количество информации в сообщении, которое уменьшает размер пространство поиска в 1/p_i раз приносит битов информации.

Примеры

Свойства энтропии Шеннона

Для случайной величины , принимающей значений с вероятностями , выполняются следующие соотношения.

.
распределение вырождено.
.
распределение равномерно.

Чем распределение ближе к равномерному, тем больше энтропия Шеннона.

Энтропия пары

Понятие энтропии Шеннона можно обобщить для пары случайных величин. Аналогично это обощается для тройки, четвёрки и т.д.

Пусть совместно распределённые случайные величины и принимают значения и , соответственно. Энтропия пары случайных величин и определяется следующим соотношением:

$H(X,Y) = sum_{i=1}^ksum_{j=1}^mPr[X = a_i, Y=b_j]cdot logfrac{1}{Pr[X = a_i, Y = b_j]}.$

Примеры

Рассмотрим эксперимент с выбрасыванием двух игральных кубиков — синего и красного.

Свойства энтропии Шеннона пары случайных величин

Для энтропии пары выполняются следующие свойства.

Условная энтропия Шеннона

Теперь давайте научимся вычислять условную энтропию одной случайной величины относительно другой.

Условная энтропия относительно определяется следующим соотношением:

Примеры

Рассмотрим снова примеры про два игральных кубика.

Свойства условной энтропии

Условная энтропия обладает следующими свойствами

Взаимная информация

Ещё одна информационная величина, которую мы введём в этом разделе — это взаимная информация двух случайных величин.

Информация в о величине (взаимная информация случайных величин и ) определяется следующим соотношением

Примеры

И снова обратимся к примерам с двумя игральными кубиками.

Свойства взаимной информации

Выполняются следующие соотношения.

. Т.е. определение взаимной информации симметрично и его можно переписать так:

Или так: .
и .
.
.

Все информационные величины, которые мы определили к этому моменту можно проиллюстрировать при помощи кругов Эйлера.

Мы пойдём дальше и рассмотрим информационную величину, зависящую от трёх случайных величин.

Пусть , и совместно распределены. Информация в о при условии определяется следующим соотношением:

Свойства такие же как и обычной взаимной информации, нужно только добавить соответствующее условие ко всем членам.

Всё, что мы успели определить можно удобно проиллюстрировать при помощи трёх кругов Эйлера.

Из этой иллюстрации можно вывести все определения и соотношения на информационные величины.

Мы не будем продолжать дальше и рассматривать четыре случайные величины по трём причинам. Во-первых, рисовать четыре круга Эйлера со всеми возможными областями — это непросто. Во-вторых, для двух и трёх случайных величин почти все возможные соотношения можно вывести из кругов Эйлера, а для четырёх случайных величин это уже не так. И в третьих, уже для трёх случайных величин возникают неприятные эффекты, демонстрирующие, что дальше будет хуже.

Рассмотрим треугольник в пересечении всех трёх кругов H(X) , H(Y) и H(Z) . Этот треугольник соответствуют взаимной информации трёх случайных величин . Проблема с этой информационной величиной заключается в том, что ей не удаётся придать какой-то «физический» смысл. Более того, в отличие от всех остальных величин на картинке может быть отрицательной!

Рассмотрим пример трёх случайных величин равномерно распределённых на {0,1} . Пусть и будут независимы, а . Легко проверить, что . При этом . В то же время . Получается следующая картинка.

Мы знаем, что . При этом . Получается, что a=b=c=1 , а d=-1 , т.е. для таких случайных величин.

Применение энтропии Шеннона: кодирование

В этом разделе мы обсудим, как энтропия Шеннона возникает в теории кодирования. Будем рассматривать коды, которые кодируют каждый символ по отдельности.

Пусть задан алфавит Sigma . Код — это отображение из Sigma в ${0,1}^*$ . Код называется однозначно декодируемым, если любое сообщение, полученное применением к символам некоторого текста, декодируется однозначно.

Код называется префиксным (prefix-free), если нет двух символов alpha и beta таких, что является префиксом C(beta) .

Префиксные коды являются однозначно декодируемыми. Действительно, при декодировании префиксного кода легко понять, где находятся границы кодов отдельных символов.

Теорема [Шеннон]. Для любого однозначно декодируемого кода существует префиксный код с теми же длинами кодов символов.

Таким образом для изучения однозначно декодируемых кодов достаточно рассматривать только префиксные коды.

Задача об оптимальном кодировании.
Дан текст . Нужно найти такой код , что

$sum_{i=1}^n |C(a_i)| to min.$

Пусть $Sigma = {alpha_1,alpha_2,dotsc,alpha_k}$ . Обозначим через f_i частоту, с которой символ alpha_i встречается в . Тогда выражение выше можно переписать как

$nsum_{i=1}^k f_icdot |C(alpha_i)| to min.$

Следующая теорема могла встречаться вам в курсе алгоритмов.

Теорема [Хаффман]. Код Хаффмана, построенный по , является оптимальным префиксным кодом.

Алгоритм Хаффмана по набору частот эффективно строит оптимальный код для задачи оптимального кодирования.

Связь с энтропией

Имеют место две следующие оценки.

Теорема [Шеннон]. Для любого однозначно декодируемого кода выполняется

$sum_{i=1}^k f_icdot|C(alpha_i)|ge sum_{i=1}^n f_icdot logfrac1{f_i}.$

Теорема [Шеннон]. Для любых значений ${f_1,f_2,dotsc,f_k}$ существует префиксный код , такой что

$sum_{i=1}^n f_icdot|C(alpha_i)|le sum_{i=1}^n f_icdot logfrac1{f_i} + 1.$

Рассмотрим случайную величину , равномерно распределённую на символах текста . Получим, что $H(X) = f_icdot logfrac1{f_i}$ . Таким образом, эти две теоремы задают оценку на среднюю длину кода символа при оптимальном кодировании, т.е. и для кодирования Хаффмана.

$H(X) le sum_{i=1}^n f_icdot|C(alpha_i)|le H(X) + 1.$

Следовательно, длину кода Хаффмана текста можно оценить, как

Применение энтропии Шеннона: шифрования с закрытым ключом

Рассмотрим простейшую схему шифрования с закрытым ключом. Шифрование сообщения с ключом шифрования выполняется при помощи алгоритма шифрования . В результате получается шифрограмма . Зная получатель шифрограммы восстанавливает исходное сообщение : .

Мы будем анализировать эту схему с помощью аппарата энтропии Шеннона. Пусть и являются случайными величинами. Противник не знает и , но знает , которая так же является случайной величиной.

Для совершенной схемы шифрования (perfect secrecy) выполняются следующие соотношения:

, т.е. шифрограмма однозначно определяется по ключу и сообщению.
, т.е. исходное сообщение однозначно восстанавливается по шифрограмме и ключу.
, т.е. в отсутствие ключа из шифрограммы нельзя получить никакой информации о пересылаемом сообщении.

Теорема [Шеннон]. , даже если условие нарушается (т.е. алгоритм использует случайные биты).

Эта теорема утверждает, что для совершенной схемы шифрования длина ключа должна быть не менее длины сообщения. Другими словами, если вы хотите зашифровать и передать своему знакомому файл размера 1Гб, то для этого вы заранее должны встретиться и обменяться закрытым ключом размера не менее 1Гб. И конечно, этот ключ можно использовать только однажды. Таким образом, самая оптимальная совершенная схема шифрования — это «одноразовый блокнот», в котором длина ключа совпадает с длиной сообщения.

Если же вы используете ключ, который короче пересылаемого сообщения, то шифрограмма раскрывает некоторую информацию о зашифрованном сообщении. Причём количество этой информации можно оценить, как разницу между энтропией сообщения и энтропией ключа. Если вы используете пароль из 10 символов при пересылке файла размера 1Гб, то вы разглашаете примерно 1Гб – 10 байт.

Это всё звучит очень печально, но не всё так плохо. Мы ведь никак не учитываем вычислительную мощь противника, т.е. мы не ограничиваем количество времени, которое противнику потребуется на выделение этой информации.

Современная криптография строится на предположении об ограниченности вычислительных возможностей противника. Тут есть свои проблемы, а именно отсутствие математического доказательства криптографической стойкости (все доказательства строятся на различных предположениях), так что может оказаться, что вся эта криптография бесполезна (подробнее можно почитать в статье о мирах Рассела Импальяццо, которая переведена на хабре), но это уже совсем другая история.

Доказательство. Нарисуем картинку для трёх случайных величин и отметим то, что нам известно.

.
, следовательно , а значит .
(по свойству взаимной информации), следовательно , а значит .
. Таким образом,

В доказательстве мы действительно не воспользовались тем, что .

Алгоритмический подход: колмогоровская сложность

Подход Шеннона хорош для случайных величин, но если мы попробуем применить его к текстам, то выходит, что количество информации в тексте зависит только от частот символов, но не зависит от их порядка. При таком подходе получается, что в «Войне и мире» и в тексте, который получается сортировкой всех знаков в «Войне и мире», содержится одинаковое количество информации. Колмогоров предложил подход, позволяющий измерять количество информации в конкретных объектах (строках), а не в случайных величинах.

Внимание. До этого момента я старался следить за математической строгостью формулировок. Для того, чтобы двигаться дальше в том же ключе, мне потребовалось бы предположить, что читатель неплохо знаком с математической логикой и теорией вычислимости. Я пойду более простым путём и просто буду махать руками, заметая под ковёр некоторые подробности. Однако, все утверждения и рассуждения дальше можно математически строго сформулировать и доказать.

Нам потребуется зафиксировать способ описания битовой строки. Чтобы не углубляться в рассуждения про машины Тьюринга, мы будем описывать строки на языках программирования. Нужно только сделать оговорку, что программы на этих языках будут запускаться на компьютере с неограниченным объёмом оперативной памяти (иначе мы получили бы более слабую вычислительную модель, чем машина Тьюринга).

Сложностью K_F(x) строки относительно языка программирования называется длина кратчайшей программы, которая выводит .

Таким образом сложность «Войны и мира» относительноя языка Python — это длина кратчайшей программы на Python, которая печатает текст «Войны и мира». Естественным образом сложность отсортированной версии «Войны и мира» относительно языка Python получится значительно меньше, т.к. её можно предварительно закодировать при помощи RLE.

Сравнение языков программирования

Дальше нам потребуется научиться любимой забаве всех программистов — сравнению языков программирования.

Будем говорить, что язык не хуже языка программирования и обозначать Fprec G , если существует константа c_G такая, что для для всех $xin{0,1}^*$ выполняется

Исходя из этого определения получается, что язык Python не хуже (!) этого вашего Haskell! И я это докажу. В качестве константы $c_text{Haskell}$ мы возьмём длину реализации интепретатора Haskell на Python. Таким образом, любая программа на Haskell переделывается в программу на Python просто дописыванием к ней интерпретатора Haskell на Python.

Соломонов и Колмогоров пошли дальше и доказали существования оптимального языка программирования.

Теорема [Соломонова-Колмогорова]. Существует способ описания (язык программирования) такой, что для любого другого способа описания выполняется Uprec F .

И да, некоторые уже наверное догадались, что — это JavaScript. Или любой другой Тьюринг полный язык программирования.

Это приводит нас к следующему определению, предложенному Колмогоровым в 1965 году.

Колмогоровской сложностью строки будем называть её сложность относительно оптимального способа описания и будем обозначать .

Важно понимать, что при разных выборах оптимального языка программирования колмогоровская сложность будет отличаться, но только на константу. Для любых двух оптимальных языков программирования F_1 и F_2 выполняется и , т.е. существует такая константа , что $|K_{F_1} - K_{F_2}| le c.$ Это объясняет, почему в этой науке аддитивные константы принято игнорировать.

При этом для конкретной строки и конкретного выбора колмогоровская сложность определена однозначно.

Свойства колмогоровской сложности

Начнём с простых свойств. Колмогоровская сложность обладает следующими свойствами.

Первое свойство выполняется потому, что мы всегда можем зашить строку в саму программу. Второе свойство верно, т.к. из программы, выводящей строку , легко сделать программу, которая выводит эту строку дважды.

Примеры

Несжимаемые строки

Важнейшее свойство колмогоровской сложности заключается в существовании сложных (несжимаемых строк). Проверьте себя и попробуйте объяснить, почему не бывает идеальных архиваторов, которые умели бы сжимать любые файлы хотя бы на 1 байт, и при этом позволяли бы однозначно разархивировать результат.

В терминах колмогоровской сложности это можно сформулировать так.

Вопрос. Существует ли такая длина строки , что для любой строки $xin{0,1}^n$ колмогоровская сложность меньше ?

Следующая теорема даёт отрицательный ответ на этот вопрос.

Теорема. Для любого существует $xin{0,1}^n$ такой, что .

Доказательство. Битовых строк длины всего 2^n . Число строк сложности меньше не превосходит число программ длины меньше , т.е. таких программ не больше чем

$1+2+dotsb +2^{n-1} = 2^n - 1 < 2^n.$

Таким образом, для какой-то строки гарантированно не хватит программы.

Верна и более сильная теорема.

Теорема. Существует c > 0 такое, что для 99% слов длины верно

Другими словами, почти все строки длины имеют почти максимальную сложность.

Колмогоровская сложность: вычислимость

В этом разделе мы поговорим про вычислимость колмогоровской сложности. Я не буду давать формально определение вычислимости, а буду опираться на интуитивные предствления читателей.

Теорема. Не существует программы, которая по двоичной записи числа выводит строку , такую что .

Эта теорема говорит о том, что не существует программы-генератора, которая умела бы генерировать сложные строки по запросу.

Доказательство. Проведём доказетельство от противного. Пусть такая программа существует и . Тогда с одной стороны сложность не меньше , а с другой стороны мы можем описать при помощи log n битов и кода программы.

Это приводит нас к противоречию, т.к. при достаточно больших значениях неизбежно станет больше, чем .

Как следствие мы получаем невычислимость колмогоровской сложности.

Следствие. Отображение не является вычислимым.

Опять же, предположим, что это нет так и существует программа , которая по строку вычисляет её колмогоровскую сложность. Тогда на основе программы можно реализовать программу из теоремы выше: она будет перебирать все строки длины не более и находить лексикографически первую, для которой сложность будет не меньше . А мы уже доказали, что такой программы не существует.

Связь с энтропией Шеннона

Теорема. Пусть длины содержит pcdot n единиц и нулей, тогда

$K(x)le left(pcdotlogfrac1p + (1-p)cdotlogfrac{1}{1-p}right)cdot n + O(log n).$

Я надеюсь, что вы уже узнали энтропию Шеннона для случайной величины с двумя значениями с вероятностями и 1-p .

Для колмогоровской сложности можно проделать весь путь, который мы проделали для энтропии Шеннона: определить условную колмогоровскую сложность, сложность пары строк, взаимную информацию и условную взаимную информацию и т.д. При этом формулы будут повторять формулы для энтропии Шеннона с точностью до . Однако это тема для отдельной статьи.

Применение колмогоровской сложности: бесконечность множества простых чисел

Начнём с довольно игрушечного применения. С помощью колмогоровской сложности мы докажем следующую теорему, знакомую нам со школы.

Теорема. Простых чисел бесконечно много.

Очевидно, что для доказательства этой теоремы никакая колмогоровская сложность не нужна. Однако на этом примере я смогу продемонстрировать основные идеи применения колмогоровской сложности в более сложных ситуациях.

Доказательство. Проведём доказательство от обратного. Пусть существует всего простых чисел: . Тогда любое натуральное раскладывается на степени простых:

$x = p_1^{k_1}cdot p_2^{k_2}cdotdotsmcdot p_m^{k_m},$

т.е. определяется набором степеней . Каждое , т.е. задаётся битами. Поэтому любое можно задать при помощи битов (помним, что — это константа).

Теперь воспользуемся теоремой о существовании несжимаемых строк. Как следствие, мы можем заключить, что существуют -битовые числа сложности не менее (можно взять сложную строку и приписать в начало единицу). Получается, что сложное число можно задать при помощи небольшого числа битов.

Противоречие.

Применение колмогоровской сложности: алгоритмическая случайность

Колмогоровская сложность позволяет решить следующую проблему из классической теории вероятностей.

Пусть в лаборатории живёт обезьянка, которую научили печатать на печатной машинке так, что каждую кнопку она нажимает с одинаковой вероятность. Вам предлагается посмотреть на лист печатного текста и сказать, верите ли вы, что его напечатала эта обезьянка. Вы смотрите на лист и видите, что это первая страница «Гамлета» Шекспира. Поверите ли вы? Очевидно, что нет. Хорошо, а если это не Шекспир, а, скажем, текст детектива Дарьи Донцовой? Скорей всего тоже не поверите. А если просто какой-то набор русских слов? Опять же, очень сомневаюсь, что вы поверите.

Внимание, вопрос. А как объяснить, почему вы не верите? Давайте для простоты считать, что на странице помещается 2000 знаков и всего на машинке есть 80 знаков. Вы можете резонно заметить, что вероятность того, что обезьянка случайным образом породила текст «Гамлета» порядка $1/80^{2000}$ , что астрономически мало. Это верно.

Теперь предположим, что вам показали текст, который вас устроил (он с вашей точки зрения будет похож на «случайный»). Но ведь вероятность его появления тоже будет порядка $1/80^{2000}$ . Как же вы определяете, что один текст выглядит «случайным», а другой — не выглядит?

Колмогоровская сложность позволяет дать формальный ответ на этот вопрос. Если у текста отстутствует короткое описание (т.е. в нём нет каких-то закономерностей, которые можно было бы использовать для сжатия), то такую строку можно назвать случайной. И как мы увидели выше почти все строки имеют большую колмогоровскую сложность. Поэтому, когда вы видите строку с закономерностями, т.е. маленькой колмогоровской сложности, то это соответствует очень редкому событию. В противоположность наблюдению строки без закономерностей. Вероятность увидеть строку без закономерностей близка к 1.

Это обобщается на случай бесконечных последовательностей. Пусть . Как определить понятие случайной последовательности?

(неформальное определение)
Последовательность случайна по Мартину–Лёфу, если каждый её префикс является несжимаемым.

Оказывается, что это очень хорошее определение случайных последовательностей, т.к. оно обладает ожидаемыми свойствами.

Свойства случайных последовательностей

Почти все последовательности являются случайными по Мартину–Лёфу, а мера неслучайных равна .
Всякая случайная по Мартину-Лёфу последовательность невычислима.
Если случайная по Мартин-Лёфу, то

$lim_{ntoinfty} frac{text{число единиц в префиксе длины n}}{n} = frac12.$

Заключение

Если вам интересно изучить эту тему подробнее, то я рекомендую обратиться к следующим источникам.

Верещагин Н.К., Щепин Е.В. Информация, кодирование и предсказание. МЦНМО. (нет в свободном доступе, но pdf продаётся за копейки)
В.А. Успенский, А.Х. Шень, Н.К. Верещагин. Колмогоровская сложность и алгоритмическая случайность.
Курс «Введение в теорию информации» А.Е. Ромащенко в Computer Science клубе.

Если вам интересны подобные материалы, подписывайтесь в соцсетях на CS клуб и CS центр, а так же на наши каналы на youtube: CS клуб, CS центр.

Источник

Определение количества информации по к. Шеннону

Статистическая
мера рассматривает информацию как исход
случайных событий. Количество информации
ставится в зависимость от априорных
вероятностей этих событий.

Пусть
некоторая физическая система
характеризуется N
состояниями х₁,
х₂,
х₃,…,
х_Nи
распределением вероятностей этих
состояний, образующих полную группу
несовместимых событий р(х₁),
р(х₂),
р(х₃),…,
р(х_N):

Американский
ученый Клод Шеннон в середине 40-х годов
прошлого столетия предложил оценивать
количество информации в каждом исходе
мерой:

(1.5)

За
количественную
меру информации

содержащуюся в некотором сообщении

принимается минус логарифм вероятности
этого сообщения

.

При

,
[бит]. (1.6)

Энтропия сообщения. Среднее количество информации по всем состояниям системы:

(1.7)

где

—
энтропия
системы.

Функция
Н была
выбрана Шенноном так, чтобы она
удовлетворяла следующим требованиям:

1.
Н
должна быть непрерывной относительно
р{х_i}.

2.
Если все р(х_i)
равны, р(х_i)=1/N,
то Н
должна быть монотонно возрастающей
функцией от N.
В случае равновероятных событий имеется
больше возможностей выбора или
неопределенности, чем в случае, когда
имеются не равновероятные события.

3.
Если бы выбор распадался на два
последовательных выбора, то первоначальная
Н
должна была бы быть взвешенной суммой
индивидуальных значений Н.

Шенноном
доказано, что существует единственная
функция Н,
вид которой приведен выше, удовлетворяющая
этим трем требованиям. Кроме того,
энтропия H
характеризуется следующими свойствами:

энтропия
всегда неотрицательна, так как значения
вероятностей выражаются дробными
величинами, а их логарифмы — отрицательными
величинами, т.е. члены — р(x_i)
logр(x_i)
— неотрицательны;
энтропия
равна нулю в том крайнем случае, когда
вероятность одного события равна
единице, а вероятности всех остальных
нулю. Это тот случай, когда об опыте или
величине все известно заранее и результат
не приносит никакой новой информации;
энтропия
имеет наибольшее значение при условии,
когда все вероятности равны между собой
р(х₁),р(х₂),…р(x_N)=1/N.
При этом

.

Таким
образом, в случае равновероятности
событий статистическое определение
количества информации по Шеннону
совпадает с определением количества
информации по Хартли. Совпадение оценок
свидетельствует о полном использовании
информационной емкости системы, т.e.
формула Хартли соответствует максимальному
значению энтропии.

Физически
это определяет случай, когда неопределенность
настолько велика, что прогнозировать
оказывается трудно.

В
случае неравенства вероятностей
количество информации по Шеннону меньше
информационной емкости системы.

Так
энтропия для двух неравновероятных
состояний одного элемента (Q=2)
равна

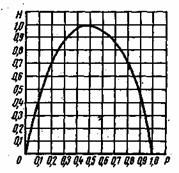
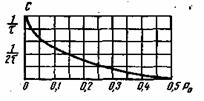
Поведение
этой функции в зависимости от значений
р₁
и р₂
показано на рис.1.3.

Максимум
Н=1
достигается при р₁=р₂=0,5,
когда два состояния равновероятны. При
р₁=1,
р₂=0
и при
р₁=0,
р₂=1,
что соответствует полной достоверности
события, энтропия равна нулю.

Кроме неравновероятности
появления символов следует учитывать,
что реальные источники вырабатывают
слова при наличии статистической
зависимости между буквами. В реальных
источниках вероятность выбора какой-либо
очередной буквы зависит от всех
предшествующих букв. Многие реальные
источники достаточно хорошо описываются
марковскими моделями источника
сообщений. Согласно указанной модели
условная вероятность выбора источником
очередной

,
буквы зависит только от

предшествующих букв.

Рассмотрим
ансамбли

и

и их произведение

.
Для любого
фиксированного

можно
построить условное распределение
вероятностей

на множестве

и для каждого

подсчитать
информацию

называемую
условной
собственной информацией
сообщения

— при фиксированном

,

Ранее
мы назвали энтропией ансамбля

среднюю
информацию сообщений

.
Аналогично,
усреднив условную информацию

по

,
получим
величину

называемую
частной
условной
энтропией
X
при
фиксированном

Вновь
введенная энтропия

— случайная
величина, поскольку она зависит от
случайной переменной

.
Чтобы
получить неслучайную информационную
характеристику пары вероятностных
ансамблей, нужно выполнить усреднение
по всем значениям

.
Величина

называется
условной
энтропией
ансамбля

при фиксированном ансамбле

.

Отметим ряд свойств
условной энтропии:

.
,
причем равенство имеет место в том и
только в том

случае,
когда ансамбли

независимы.

3. Совместная
энтропия

4.
.

5.

,
причем равенство
имеет место в том и только в том случае,
когда ансамбли

условно независимы при всех

.

Обсудим
физический смысл сформулированных
свойств условной энтропии. Свойство
2 устанавливает, что условная энтропия
ансамбля не превышает его безусловной
энтропии. Свойство 5 усиливает это
утверждение. Из него следует, что условная
энтропия не увеличивается с увеличением
числа условий. Оба эти факта не удивительны,
они отражают то обстоятельство, что
дополнительная информация об ансамбле

,
содержащаяся
в сообщениях других ансамблей, в
среднем
уменьшает
информативность (неопределенность)
ансамбля

Из
свойств 1-5 следует неравенство

в
котором равенство возможно только в
случае совместной независимости
ансамблей

.

Напомним, что
вычисление энтропии — это определение
затрат на передачу или хранение букв
источника. Свойства условной энтропии
подсказывают, что при передаче буквы

следует
использовать то обстоятельство, что
предыдущие буквы

уже известны на приемной стороне. Это
позволит вместо

бит потратить меньшее количество

бит.

Соседние файлы в папке Лекции

Источник

6.1. Мера количества информации

6.2. Энтропия источника дискретных сообщений

6.3. Статистические свойства источников сообщений

6.4. Скорость передачи информации и пропускная способность дискретного канала без помех

6.5. Оптимальное статистическое кодирование сообщений

6.6. Скорость передачи информации и пропускная способность дискретных каналов с помехами

6.7. Теорема Шеннона для дискретного канала с помехами

6.8. Энтропия непрерывных сообщений

6.9. Скорость передачи и пропускная способность непрерывного канала. Формула Шеннона

6.10. Пропускная способность каналов с переменными параметрами

6.11. Эффективность систем передачи информации

6.1. Мера количества информации

В теории информации изучаются количественные закономерности передачи, хранения ,и обработки информации.

Назначение любой системы связи — передать в течение заданного времени как можно больше достоверных сведений от одного объекта или корреспондента к другому.

Проблема достоверности при различных способах приема и передачи сообщений рассматривалась в теории помехоустойчивости. Эта теория, как мы убедились, позволяет не только найти достоверность передачи при заданных условиях, но и выяснить, при каких методах передачи и обработки сигналов эта достоверность будет наибольшей.

В теории информации основное внимание уделяется определению средней скорости передачи информации и решению задачи максимизации этой скорости путем применения соответствующего кодирования [13]. Предельные соотношения теория информации позволяют оценить эффективность различных систем связи и установить условия согласования, в информационном отношении источника с каналом и канала с потребителем.

Для исследования этих вопросов с общих позиций необходимо прежде всего установить универсальную количественную меру информации, не зависящую от конкретной физической природы передаваемых сообщений. Когда принимается сообщение о каком-либо событии, то наши знания о нем изменяются. Мы получаем при этом некоторую информацию об этом событии. Сообщение о хорошо известном нам событии, очевидно, никакой информации не несет. Напротив, сообщение о малоизвестном событии содержит много информации. Например, сообщение бюро погоды от 20 июня о том, что в Одессе «завтра выпадет снег» несет больше информации, чем сообщение «завтра ожидается ясная погода». Первое сообщение является неожиданным, оно несет сведения о редком, маловероятном явлении и поэтому содержит много информации. Второе сообщение является весьма вероятным, оно содержит мало нового и поэтому несет мало информации.

Таким образом, количество информации в сообщении о некотором событии существенно зависит от вероятности этого события.

Вероятностный подход и положен в основу определения меры количества информации. Для количественного определения информации, в принципе, можно использовать любую монотонно убывающую функцию вероятности F[P(a)] где Р(а) — вероятность, сообщения а. Простейшей из них является функция F=1/Р(а) которая характеризует меру неожиданности (неопределенности) сообщения. Однако удобнее исчислять количество информации а логарифмических единицах, т. е. определять количество информации в отдельно взятом сообщении как

(6.1)

Так как 0<P(a)l, то J(a) — величина всегда положительная и конечная. При Р(а)=1 количество информации равно нулю, т. е., сообщение об известном событии никакой информации не несет. Логарифмическая мера обладает естественным в данном случае свойством аддитивности, согласно которому количество информации, содержащееся в нескольких независимых сообщениях, равна сумме количества информации в каждом из них. Действительно, так как совместная вероятность п независимых сообщений , то количество информации а этих сообщениях равно: , что соответствует интуитивным представлениям об увеличении информации при получении дополнительных сообщений. Основание логарифма k может быть любым. Чаще всего принимают k=2, и тогда количество информации выражается в двоичных единицах: дв. ед.

Двоичную единицу иногда называют бит. Слово бит произошло от сокращения выражения binary digit (двоичная цифра). В двоичных системах связи для передачи сообщения используется два символа, условно .обозначаемых 0 и 1. В таких системах при независимых и равновероятных символах, когда P(0)=P(1)=1/2, каждый из них несет одну двоичную единицу информации:

Формула (6.1) позволяет вычислять количество информация в. сообщениях, вероятность которых отлична от нуля. Это, в свою очередь, предполагает, что сообщения дискретны, а их число ограничено. В таком случае принято говорить об ансамбле сообщений, который описывается совокупностью возможных сообщений и их вероятностей:

(6.2)

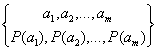
Ансамбль сообщений образует полную группу событий, поэтому всегда .

Если все сообщения равновероятны:, то количество информации в каждом из них определяется величиной

(6.3)

Отсюда следует, что количество информации в сообщении зависит от ансамбля, из которого, оно выбрано. До передачи сообщения имеется неопределенность относительно того, какое из m сообщений ансамбля будет передано после приема сообщения эта неопределенность снимается. Очевидно, чем больше т, тем больше неопределенность и тем большее количество информации содержится в переданном сообщении.

Рассмотрим пример. Пусть ансамбль возможных сообщений представляет собой алфавит, состоящий из m различных букв. Необходимо определить, какое количество информации содержится в передаваемом слове длиной п букв, если вероятности появления букв одинаковы, а сами буквы следуют независимо друг от друга. Количество информации при передаче одной буквы:. Так как все буквы равновероятны, то и количество информации, содержащееся в любой букве,. Буквы следуют независимо поэтому количество информации в слове из п букв

К определению информации можно подойти и с другой стороны. Будем рассматривать в качестве сообщения не отдельную букву, а целое слово. Если все буквы равновероятны и следуют независимо, то все слова будут также равновероятны и , где N=mⁿ — число возможных слов. Тогда можно записать

Для двоичного кода ансамбль элементарных сообщений состоит из двух элементов 0 и 1 (m=2). В этом случае сообщение из п элементов несет информацию,

(6.4)

В общем случае при передаче сообщений неопределенность снимается не полностью. Так, в канале с шумами возможны ошибки. По принятому сигналу v только с некоторой вероятностью можно судить о том, что было передано сообщение а. Поэтому после получения сообщения остается некоторая неопределенность, характеризуемая величиной апостериорной вероятности P(a/v), а количество информации, содержащееся в сигнале v, определяется степенью уменьшения неопределенности при его приеме. Если Р(а) — априорная ,вероятность, то количество информации в принятом сигнале v относительно переданного сообщения а, очевидно, будет равно:

(6.5)

Это выражение можно рассматривать также как разность между количеством информации, поступившим от источника сообщений, и тем количеством информации, которое потеряло в канале за счет действия шумов.

6.2. Энтропия источника дискретных сообщений

Энтропия источника независимых сообщений. До сих пор определялось количество информации, содержащееся в отдельных сообщениях. Вместе с тем во многих случаях, когда требуется согласовать канал с источником сообщений, таких сведений оказывается недостаточно. Возникает потребность. в характеристиках, которые, бы позволяли оценивать информационные свойства источника сообщений в целом. Одной из важных характеристик такого рода является среднее количество информации, приходящееся на одно сообщение.

В простейшем случае, когда все сообщения равновероятны, количество информации в каждом из них одинаково и, как было показано выше, определяется выражением (6.3). При этом среднее количество информации равно log т. Следовательно, при равновероятных независимых сообщениях информационные свойства источника зависят только от числа сообщений в ансамбле т.

Однако в реальных условиях сообщения, как правило, имеют разную вероятность. Так, буквы алфавита О, Е, А встречаются в тексте сравнительно часто, а буквы Щ, Ы, Ъ — редко. Поэтому знание числа сообщений т в ансамбле является недостаточным, необходимо иметь сведения о вероятностях каждого сообщения: .

Так как вероятности сообщений неодинаковы, то они несут различное количество информации J(a)=—logP(a). Менее вероятные сообщения несут большее количество информации и наоборот. Среднее количество информации, приходящееся на одно сообщение источника, определяется как математическое ожидание J(a):

(6.6)

Величину Н(а) называется энтропией. Этот термин заимствован из термодинамики, где имеется аналогичное по своей форме выражение, характеризующее неопределенность состояния физической системы. В теории информации энтропия Н(а) также характеризует неопределенность ситуации до передачи сообщения, поскольку заранее неизвестно, какое из сообщений ансамбля источника будет передано. Чем больше энтропия, тем сильнее неопределенность и тем большую информацию в среднем несет одно сообщение источника.

В качестве примера вычислим энтропию источника сообщений, который характеризуется ансамблем, состоящим из двух сообщений и с вероятностями и . На основании (6.6) энтропия такого источника будет равна:

Рис. 6.1. Зависимость энтропии от вероятности р

Зависимость Н(а) от р показана на рис. 6.1. Максимум имеет место при р=1/2, т. е. когда ситуация является наиболее неопределенной. При р=1 или р⁼0, что соответствует передаче одного из сообщений или , неопределенность отсутствует. В этих случаях энтропия Н(а) равна нулю.

Среднее количество информации, содержащееся в последовательности из п сообщений, равно:

Отсюда следует, что количество передаваемой информации можно увеличить не только за счет увеличения числа сообщений, но и путем повышения энтропии источника, т. е. информационной емкости его сообщений.

Обобщая полученные выше результаты, сформулируем следующие основные свойства энтропии источника независимых сообщений (6.6):

— энтропия— величина всегда положительная, так как

— при равновероятных сообщениях, когда , энтропия максимальна и равна:

(6.7)

— энтропия равняется нулю лишь в том случае, когда все вероятности Р(a) равны нулю, за исключением одной, величина которой ,равна единице;

— энтропия нескольких независимых источников равна сумме энтропии этих источников .

Энтропия источника зависимых сообщений. Рассмотренные выше источники независимых дискретных сообщений являются простейшим типом источников. В реальных условиях картина значительно усложняется из-за наличия статистических связей между сообщениями. Примерам может быть обычный текст, где появление той или иной буквы зависит от предыдущих буквенных сочетаний. Так, например, после сочетания ЧТ вероятность следования гласных букв О, Е, И больше, чем согласных.

Статистическая связь ожидаемого сообщения с предыдущим сообщением количественно оценивается совместной вероятностью или условной вероятностью , которая выражает вероятность появления сообщения при условии, что до этого было передано сообщение аКоличество информации, содержащееся в сообщении , при условии, что известно предыдущее сообщение а согласно (6.1) будет равно:. Среднее количество информации при этом определяется условной энтропией , которая вычисляется как математическое ожидание информации по всем возможным сообщениям аи . Учитывая соотношение (2.25), .получаем

(6.8)

В тех случаях, когда связь распространяется на три сообщения , условная энтропия источника определяется аналогичным соотношением

(6.9)

В общем случае n зависимых сообщений

(6.10)

Важным свойством условной энтропии источника зависимых сообщений является то, что при неизменном количестве сообщений в ансамбле источника его энтропия уменьшается с увеличением числа сообщений, между которыми существует статистическая взаимосвязь. В соответствии с этим свойством, а также свойством энтропии источника независимых сообщений можно записать неравенства

(6.11)

Таким образом, наличие статистических связей между сообщениями всегда приводит к уменьшению количества информации, приходящегося в среднем на одно сообщение.

Избыточность источника сообщений. Уменьшение энтропии источника с увеличением статистической взаимосвязи (6.11) можно рассматривать как снижение информационной емкости сообщений. Одно и то же сообщение при наличия взаимосвязи содержит в среднем меньше информации, чем при ее отсутствии. Иначе говоря, если источник создает последовательность сообщений, обладающих статистической связью, и характер этой связи известен, то часть сообщений, выдаваемая источником, является избыточной, так как она может быть восстановлена по известным статистическим связям. Появляется возможность передавать сообщения в сокращенном виде без потери информации, содержащейся в них. Например, при передаче телеграммы мы исключаем из текста союзы, предлоги, знаки препинания, так как они легко восстанавливаются, при чтении телеграммы на основании известных правил построения фраз и слов.

Таким образом, любой источник зависимых сообщений, как принято говорить, обладает избыточностью. Количественное определение избыточности может быть получено из следующих соображений. Для того чтобы передать количество информации, источник без избыточности должен выдать в среднем сообщений, а источник с избыточностью сообщений.

Поскольку и , то для передачи одного и того же количества информации источник с избыточностью должен использовать большее количество сообщений. Избыточнее количество сообщений равно kn—k0, а избыточность определяется как отношение

(6.12)

Величина избыточности лежит в пределах и согласно (6.11) является неубывающей функцией п. Для русского языка, например, дв. ед., , , дв. ед. Отсюда на основании (6.12) для русского языка получаем избыточность порядка 50%.

Коэффициент

(6.13)

называется коэффициентом сжатия. Он показывает, до какой величины можно сжать передаваемые сообщения, если устремить избыточность. Источник, обладающий избыточностью, передает излишнее количество сообщений. Это увеличивает продолжительность передачи и снижает эффективность использования канала связи. Сжатие сообщений можно осуществить посредством соответствующего кодирования. Информацию необходимо передавать такими сообщениями, информационная емкость которых используется наиболее полно. Этому условию удовлетворяют равновероятна и независимые сообщения.

Вместе с тем избыточность источника не всегда является отрицательным свойством. Наличие взаимосвязи между буквами текста дает возможность восстанавливать его при искажении отдельных букв, т. е. использовать избыточность для повышения достоверности передачи информации.

6.3. Статистические свойства источников сообщений

Использование энтропия в качестве усредненной величины, количественно характеризующей информационные свойства источника, выдающего последовательности дискретных сообщений, является целесообразным при условии, что вероятностные соотношения для этих последовательностей сохраняются неизменными. Источник называют стационарным, когда распределение вероятностей сообщений не зависит от их места в последовательности сообщений, создаваемых этим источником, т. е.

(6.14)

где п — любое целое число.

По аналогии со стационарным случайным процессом статистические характеристики последовательности сообщений стационарного источника не зависят от выбора начала отсчета.

Среди стационарных источников сообщений важное место занимают эргодические источники, которые отличаются тем, что с вероятностью, близкой к единице, любая достаточно длинная последовательность сообщений такого источника полностью характеризует его статистические свойства. Важной особенностью эргодических источников является то, что статистическая взаимосвязь между сообщениями всегда распространяется только на конечное число предыдущих сообщений.

Существует стационарные источники, которые могут работать в различных режимах, отличающихся друг от друга своими статистическими характеристиками. В этом случае источник не является эргодическим, так как при работе в одном режиме даже продолжительная последовательность сообщений уже не может в целом характеризовать свойства источника.

Условная энтропия стационарного источника находится как результат усреднения по всем режимам работы

(6.15)

где ) — вероятность и условная энтропия j-го режима работы.

Рассмотрим условную энтропию при заданной последовательности предыдущих сообщений

(6.16)

Здесь символом обозначена последовательность п—1 предыдущих сообщений , причем индексом а нумеруются все возможные соединения из т сообщений по п—1, т. е. всего последовательностей

Последовательность можно трактовать как состояние источника, в котором он находится после ее передачи. Подобного рода случайные последовательности (обладающие эргодическими свойствами) известны в математике как дискретные цепи А. А. Маркова.

В марковском эргодическом источнике вероятность передачи того или иного сообщения однозначно определяется состоянием источника. После передачи сообщения источник переходит в новое состояние, которое зависит от предыдущего состояния и переданного сообщения.

Достаточно длинные эргодические последовательности сообщений, с высокой степенью вероятности содержащие все сведения о статистических характеристиках источника, называются типичными. Чем длиннее последовательность, тем больше вероятность того, что она является типичной. В типичных последовательностях частота появления отдельных сообщений или групп сообщений сколь угодно мало отличается от их вероятности. Отсюда вытекает важное свойство типичных последовательностей, состоящее в том, что типичные последовательности одинаковой длины примерно равновероятны. Это легко показать для последовательностей независимых сообщений.

Предположим, что ансамбль сообщений состоит из m сообщений: и нас интересует вероятность того, что в последовательности длиной в п сообщений число сообщений аравно k, число сообщений а равно k и т. д., am соответствует km, причем . При независимых сообщениях эта вероятность, очевидно, равна:

(6.17)

где P — вероятность сообщения а. Так как во всех типичных последовательностях по определению выполняется условие , то вероятности типичных последовательностей приблизительно одинаковы и равны:

(6.18)

В этом случае количество информация в любой из типичных последовательностей

(6.19).

С другой стороны, величину Jn можно выразить через энтропию. источника Н(а):

(6.20)

Используя выражения (6.19) и (6.20), энтропию источника можно определить как

(6.21)

Для общего случал, в том числе и для зависимы сообщений, ib теории информации доказывается следующая теорема. Все эргодические последовательности, содержащие достаточно большое число сообщений п, могут быть разбиты на две группы:

— типичные последовательности с вероятностями Рп, для которых удовлетворяется неравенство

(6.22)

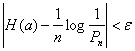
где Н(а) — энтропия источника и ε — сколь угодно малая величина;

— нетипичные последовательности, суммарная вероятность которых δ сколь угодно мала.

Величины ε и δ неограниченно уменьшаются с ростом п, что позволяет всегда выбрать такое значение п, при котором все последовательности источника, за исключением весьма малой их части могут быть отнесены к равновероятным типичным последовательностям.

Важным следствием теоремы является возможность установления зависимости между числом вариантов всевозможных типичных последовательностей Мпи энтропией источника. Для достаточно длинных последовательностей величины ε и δ малы. Тогда на основании (6.22)

(6.23)

Что касается нетипичных последовательностей, то вследствие их малой вероятности при большом п они во многих случаях вообще не учитываются.

6.4. Скорость передачи информации и пропускная способность дискретного канала без помех

Передача информации происходит во времени, поэтому можно ввести понятие скорости передачи как количества информации, передаваемой в среднем за единицу времени. Для эргодических последовательностей сообщений, где допускается усреднение времени, скорость передачи равна:

(6.24)

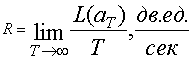
Здесь — количество информация, содержащейся в последовательности сообщений аТ, общая длительность которых равна Т, причём предполагается, что все сообщения, входящие в последовательность аТ, имеют определенную длительность.

Количество информации, создаваемое источником сообщений в среднем за единицу времени, называется производительностью источника . Эту величину удобно выразить через энтропию источника Н(а). Действительно, при можно считать и , где п — число сообщений, а — средняя длительность одного сообщения. Тогда, подставляя в (6.24) значения J(aT) и Т, получим

(6.25)

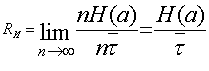
Величина для независимых сообщений может быть вычислена как математическое ожидание

(6.26)

где P()=P() — вероятность сообщения длительностью . Если длительность всех сообщений одинакова и равна , выражение (6.25) принимает вид

(6.27)

Отсюда следует, что наибольшей производительностью обладает источник с максимальной энтропией (§ 6.7), т.е.

(6.28)

Выданная источником информация в виде отдельных сообщений поступает в канал связи, где осуществляются кодирование и ряд других преобразований, в результате которых информация переносится уже сигналами и, имеющими другую природу и в общем случае обладающими другими статистическими характеристиками. Для сигналов также может быть найдена скорость передачи информации по каналу связи

(6.29)

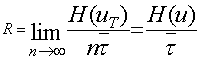
Высокая скорость передачи информации является одним из основных требований, предъявляемых к системам связи. Однако в реальных условиях существует ряд причин, ведущих к ее ограничению. Остановимся на некоторых из них.

В реальном канале число используемых сигналов т всегда конечно, поэтому энтропия в соответствии с (6.7) есть величина ограниченная:

(6.30)

С другой стороны, уменьшение длительности сигналов приводит как известно, к расширению их спектра, что ограничивается полосой пропускания канала. Это в конечном счете ставит предал уменьшению и средней длительности . Таким образом, существуют, по крайней мере, две причины: конечное число сигналов я конечная длительность сигналов, которые не позволяют беспредельно повышать скорость передачи информации по каналу связи.

Максимально возможная скорость передачи информации по каналу связи при фиксированных ограничениях называется пропускной способностью канала:

(6.31)

Пропускная способность канала характеризует его предельные возможности в отношении передачи среднего количества информации за единицу времени. Максимум скорости R в выражение (6.31) ищется по всем возможным ансамблям сигналов и,

Определим пропускную способность канала, в котором существуют два ограничения: число используемых сигналов не должно превышать т,_ а длительность их не может быть меньше т, сек. Так как Н(и) и независимы, то согласно выражению (6.31) следует искать раздельно максимум Н(и) и минимум . Тогда

(6.32)

Для двоичных сигналов т=2 и пропускная способность

(6.33)

т. е. совпадает со скоростью телеграфирования в бодах. При передаче информации простейшими двоичными сигналами — телеграфными посылками — необходимая полоса пропускания канала зависит от частоты манипуляции FM⁼1/2T, которая по определению равна частоте первой гармоники спектра сигнала, представляющего собой периодическую последовательность посылок и пауз. Очевидно, минимальная полоса пропускания канала, при которой еще возможна передача сигналов, F=FM. Отсюда максимальная скорость передачи двоичных сигналов по каналу без помех равна: С=V=2FM (предел Найквиста).

Понятие пропускной способности применимо не только ко всему каналу в целом, но и к отдельным, его звеньям. Существенным здесь является то, что пропускная способность С’ какого-либо звена не превышает пропускной способности С» второго звена, если оно расположено внутри первого. Соотношение С’С» обусловлено возможностью появления дополнительных ограничений, накладываемых на участок канала при его расширении, и снижающих пропускную способность.

6.5. Оптимальное статистическое кодирование сообщений

Для дискретных каналов без помех Шенноном была доказана следующая теорема: если производительность источника , где ε — сколь угодно малая величина, то всегда существует способ кодирования, позволяющий передавать по каналу все сообщения источника. Передачу всех сообщений при осуществить невозможно.

Смысл теоремы сводится к тому, что как бы ни была велика избыточность источника, все его сообщения могут быть переданы по каналу, если. Обратное утверждение теоремы легко доказывается от противного. Допустим, , но для передачи всех сообщений источника по каналу необходимо, чтобы скорость передачи информации R была не меньше . Тогда имеем , что невозможно, так как по определению пропускная способность .

Для рационального использования пропускной способности канала необходимо применять соответствующие способы кодирования сообщений. Статистическим или оптимальным называется кодирование, при котором наилучшим образом используется пропускная способность канала без помех. При оптимальном кодировании фактическая скорость передачи информации по каналу R приближается к пропускной способности С, что достигается путем согласования источника с каналом. Сообщения источника кодируются таким образом, чтобы они в наибольшей степени соответствовали ограничениям, которые накладываются на сигналы, передаваемые по каналу связи. Поэтому структура оптимального кода зависит как от статистических характеристик источника, так и от особенностей канала.

Рассмотрим основные принципы оптимального кодирования на примере источника независимых сообщений, который необходимо согласовать с двоичным каналом без помех. При этих условиях процесс кодирования заключается в преобразовании сообщений источника в двоичные кодовые комбинации. Поскольку имеет место однозначное соответствие между сообщениями источника и комбинациями кода, то энтропия кодовых комбинаций равна энтропии источника:

(6.34)

а скорость передачи информации в канале определяется на основании (6.29) отношением

(6.35)

Здесь — средняя длительность кодовой комбинации, которая в общем случае неравномерного кода записывается по аналогии с выражением (6.26) как

(6.36)

где — длительность одного элемента кода и, — число элементов в комбинации, присваиваемой сообщению .

Подстановка в ф-лу (6.35) выражений (6.6) и (6.36) приводит к соотношению

(6.37)

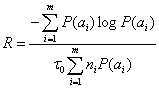
в котором числитель определяется исключительно статистическими свойствами источника, а величина — характеристиками канала. При этом возникает вопрос, можно ли так закодировать сообщения, чтобы скорость передачи R (6.37) достигла своего максимального значения, равного пропускной способности двоичного канала С=1/. Легко заметить, что это условие выполняется, если

(6.38)

что соответствует минимуму и максимуму R. Очевидно, выбор <J() не имеет смысла, так как в этом случае R>C, что противоречит выше доказанному утверждению теоремы Шеннона.

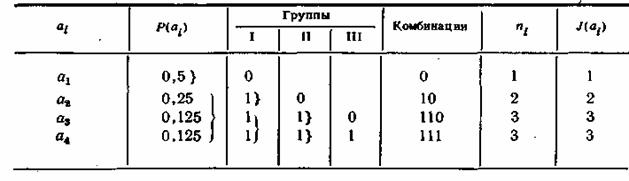
Одним из кодов, удовлетворяющих условию (6.38), является код Шеннона-Фано. Для ознакомления с принципами его построения рассмотрим в качестве примера источник сообщений, вырабатывающий четыре сообщения и с вероятностями: ; ;

Все сообщения выписываются в кодовую таблицу (табл. 6.1) в порядке убывания их вероятностей. Затем они разделяются на две группы так, чтобы суммы их вероятностей то возможности были одинаковыми. В данном примере в первую группу входит сообщение с вероятностью и во вторую — сообщения и с суммарной вероятностью, также равной 0,5.

Комбинациям, которые соответствуют сообщениям первой группы, притаивается в качестве первого символа кода 0, а комбинациям второй группы -1. Каждая из двух групп опять делится на две группы с применением того же правила присвоения символов 0 и 1.

Таблица 6.1

В идеальном случае после первого деления вероятности каждой группы должны быть равны 0,5, после второго деления— 0,25 и т. д. Процесс деления продолжается до тех пор, пока в группах не останется по одному сообщению.

При заданном распределении вероятностей сообщений код получается неравномерным, его комбинации имеют различное число элементов пi, причем, как нетрудно заметить, такой способ кодирования обеспечивает выполнение условия (6.38) полностью для всех сообщений.

В неравномерных кодах при декодировании возникает трудность в определении границ между комбинациями. Для устранения возможных ошибок обычно применяются специальные разделительные знаки. Так, в коде Морзе между буквами передается разделительный знак в виде паузы длительностью в одно тире. Передача разделительных знаков занимает дополнительное время, что снижает скорость передачи информации.

Важным свойством кода Шеннона—Фано является то, что, несмотря на его неравномерность, здесь не требуются разделительные знаки. Это обусловлено тем, что короткие комбинации не являются началом более длинных комбинаций. Указанное свойство легко проверить на примере любой последовательности:

Таким образом, все элементы закодированного сообщения несут полезную информацию, что при выполнении условия (6.38) позволяет получить максимальную скорость передачи. Она может быть найдена также путем непосредственного вычисления по ф-ле (6.37)’

(6.39)

Для сравнения рассмотрим кодирование тех же четырех сообщений ,, , с применением обычного равномерного двоичного кода. Количество комианаций при этом определяется выражением где n — число элементов в комбинации. Так как m=4, то , а длительность каждой комбинации 2. Производя вычисления по аналогии с (6.39), получим

Пропускная способность в этом случае используется только частично. Из выражения (6.38) вытекает основной принцип оптимального кодирования. Он сводится к тому, что наиболее вероятным сообщениям должны присваиваться короткие комбинации, а сообщениям с малой вероятностью — более длинные комбинации.

Возможность оптимального кодирования по методу Шеннона—Фано доказывает, что сформулированная выше теорема справедлива, по крайней мере, для источников независимых сообщений. Теорема Шеннона может быть доказана и для общего случая зависимых сообщений.

Одним из способов оптимального кодирования зависимых сообщений является применение так называемых «скользящих» кодов, основная идея которых состоит в том, что присвоение кодовых комбинаций по правилу Шеннона—Фано производится с учетом условных, а не априорных вероятностей сообщений. Число элементов в кодовой комбинации выбирается как , т. е. текущему сообщению присваивается та или иная комбинация в зависимости от того, какие сообщения ему предшествовали.

Необходимо подчеркнуть, что при оптимальном способе кодирования в сигналах, передающих сообщения источника, совершенно отсутствует какая-либо избыточность. Устранение избыточности приводит к тому, что процесс декодирования становится весьма чувствительным к воздействию помех. Это особенно сильно проявляется при оптимальном кодировании зависимых сообщений. Например, в «скользящих» кодах одна единственная ошибка может вызвать неправильное декодирование всех последующих сигналов. Поэтому оптимальные коды применимы только для каналов, в которых влияние помех незначительно.

Отличительной особенностью рассмотренных ранее каналов без помех является то, что при выполнении условия теоремы Шеннона количество принятой информации на выходе канала всегда равно количеству информации, переданной от источника сообщений. При этом, если на вход канала поступил сигнал , то на выходе возникает сигнал , вполне однозначно определяющий переданный сигнал . Количество информация, прошедшее по каналу без помех в случае передачи и приема равно количеству информации, содержащейся в сигнале :

(6.40)

Здесь величина вероятности P() характеризует ту неопределенность в отношении сигнала , которая существовала до его передачи. После приема в силу однозначного соответствия между и неопределенность полностью устраняется.

Иное положение имеет место в каналах, где присутствуют различного рода помехи. Их воздействие на передаваемый сигнал приводит к разрушению и необратимой потере части информации, поступающей от источника сообщения. Поскольку в канале с помехами принятому сигналу может соответствовать передача одного из нескольких сигналов и, то после приема остается некоторая неопределенность в отношении переданного сигнала. Здесь соответствие между u и v носит случайный характер, поэтому степень неопределенности характеризуется условной апостериорной вероятностью P(), причем всегда P()<1. Количество информации, необходимое для устранения оставшейся неопределенности , очевидно, равно той части информации, которая разрушена вследствие действия помех. Тогда в соответствии с ф-лой (6.5) количество принятой информации определяется как разность

(6.41)

Для оценки среднего количества принятой информации при передаче одного сообщения выражение (6.41) необходимо усреднить по всему ансамблю и и v:

(6.42)

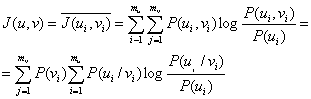
где P() = p()p() — совместная вероятность переданного и принятого сигналов, ти— количество сигналов и в ансамбле на входе канала и тv — количество сигналов ib ансамбле на выходе канала (в общем случае ).

Величина J(u,v) характеризует в среднем количество информации, которое содержит принятый сигнал v относительно переданного сигнала и, поэтому ее называют также средней взаимной информацией между и и v.

Выражение (6.42) обычно представляют в двух формах. Первая из них

(6.43)

где

— энтропия источника сигналов u и

(6.45)

— условная энтропия или ненадежность.

Соотношение (6.43) показывает, что среднее количество, принятой информации равно среднему количеству переданной информации Н(и) минус среднее количество информации H(u/v), потерянное в канале вследствие воздействия помех.

Вторая форма записи средней взаимной информации, может быть получена, если в (6.42) подставить выражение для условной вероятности в соответствии с ф-лой (2.26). После соответствующих преобразований получаем

(6.46)

Здесь

(6.47)

энтропия выхода канала и

(6.48)

— условная энтропия, равная, как будет показано ниже, энтропии шума. Она определяет бесполезную часть информации, которая содержится в принятых сигналах за счет действия помех.

Понятия скорости передачи информации и пропускной способности, введенные в § 6.7 для каналов без помех, могут быть использованы и в каналах с помехами. В этом случае скорость передачи информации ло каналу определяется как

(6.49)

где и — соответственно последовательности передаваемых и принимаемых сигналов длительностью Т.

Необходимым условием применимости ф-лы (6.49) является соблюдение свойства эргодичности как для последовательности иT, так и последовательности vT,. Последнее означает, что помехи, действующие в канале, также должны быть эргодическими. По аналогии с (6.29) скорость передачи можно представить с учетом (6.43) и (6.46) в более удобных формах:

(6.50)

Пропускная способность канала с помехами определяется как максимально возможная скорость передачи при заданных ограничениях, накладываемых на передаваемые сигналы:

(6.51)

Для каналов с сигналами одинаковой длительности, равной τ, пропускная способность

(652)

где максимум ищется по всем возможным ансамблям сигналов u.

Рассмотрим двоичный канал с помехами без памяти, по которому передаются дискретные сигналы, выбранные да ансамбля, содержащего два независимых сигнала u1 и u2 с априорными вероятностями p(u1) и p(u2). На выходе канала образуются сигналы v1 и v2 при правильном приеме отражающие соответственно сигналы u1 и u2. В результате действия помех возможны ошибки, которые характеризуются при передаче u1 условной вероятностью P(), при передаче и2— условной вероятностью P(). Вычислим энтропию сигнала (6.47)

(6.53)

и энтропию шума (6.48)

(6.54)

Будем полагать канал симметричным. Для такого канала вероятности переходов одинаковы: , а полная вероятность ошибки

(6.55)

Отсюда вытекают соотношения:

(6.56)

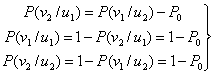
После их подстановки в выражение (6.54) получаем

(6.57)

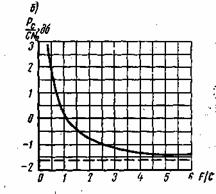
Рис. 6.2. Зависимость пропускной способности двоичного канала от вероятности ошибки Ро

Для того чтобы определить пропускную способность (6.52), необходимо максимизировать J(u,v)=H(v)-H(v/u). При заданной вероятности ошибки, как следует из (6.57), величина H(v/u) .постоянна, а максимум следует искать, изменяя H(v). Энтропия сигнала H(v), выраженная ф-лой (6.53), имеет максимальное значение H0(v)=1 случае равновероятных сигналов, когда P()=P()=0,5. Подставляя выражения (6.53) и (6.57) в ф-лу (6.52) получим следующее выражение для пропускной способности двоичного симметричного канала:

(6.58)

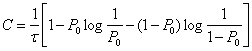
Для многопозиционного симметричного канала при mu=mv=m>2

(6.59)

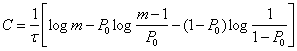
На рис. 6.2 приведена зависимость С от вероятности ошибки для двоичного канала (6.58). Увеличение Р0приводит к снижению пропускной способности, которая становится равной нулю при P0=0,5. В этом случае в соответствии с (6.56) полностью исчезает какая-либо зависимость между передаваемыми и принятыми сигналами: и . Значение P0=1/2 для бинарного канала является предельным.

6.7. Теорема Шеннона для дискретного канала с помехами

Для дискретных каналов с помехами Шеннон доказал теорему, имеющую фундаментальное значение в теории передачи информации. Эта теорема может быть сформулирована следующим образом.

Если производительность источника, где ε — сколь угодно малая величина, то существует способ кодирования, позволяющий передавать все сообщения источника со сколь угодно малой вероятностью ошибки. При такая передача невозможна.

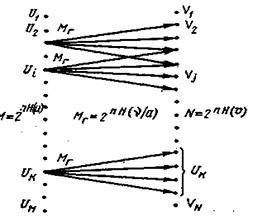
Предположим, на вход канала поступают сигналы и, которые вызывают, на его выходе сигналы v. Предварительно будем полагать, что по каналу могут передаваться исключительно типичные последовательности (§6.3), состоящие из п сигналов и:. Соответственно на выходе канала сигналы при достаточно большом п образуют типичные последовательности: , содержащие типичные последовательности ошибок. Общее число типичных последовательностей и на основании (6.23) равно:

где Н(и) — энтропия сигналов и. Соответственно число типичных последовательностей V определяется как

(6.60)

где H(v) — энтропия сигналов v.

Рис. 6.3. Схема переходов типичных последовательностей сигналов от входа к выходу канала с шумами

Действие помех проявляется в том, что нарушается однозначное соответствие между последовательностями U и V, т. е. при передаче некоторой последовательности Ui возможно появление на выходе канала одной из нескольких последовательностей V. Процесс передачи в этих условиях можно представить так, как показано на рис. 6.3, где стрелками отмечены переходы от типичных последовательностей V к типичным последовательностям V. Так как последовательности ошибок типичные, то и переходы от U к V также являются типичными. Каждой последовательности U соответствует определенная группа типичных переходов, которая характеризует неопределенность, возникающую при передаче U. Количественно указанная неопределенность описывается произведением nH(v/u), где H(v/u) — условная энтропия сигналов при передаче сообщений и (6.48). Тогда в соответствии с (6.23) количество типичных переходов в каждой группе

(6.61)

В общем случае переходы перекрещиваются, т. е. одна и та же последовательность может образоваться в результате передачи одной из нескольких последовательностей U. Для того чтобы иметь возможность с высокой точностью однозначно определить принадлежность принятой последовательности V переданной последовательности U (на рис. 6.3 этому условию удовлетворяет. U), очевидно, необходимо между грушами последовательностейV установить достаточный интервал. Поэтому из всего набора последовательностей U только часть может использоваться для передачи информации.

Обозначим последовательности, выбранные для переноса информации, через UИ, а их число — буквой МИ. Выясним взаимосвязь МИс вероятностью ошибки при определении принадлежности V, т. е. взаимосвязь с вероятностью ошибки при декодирования принятых сигналов. Вероятности всех типичных переходов от U, к V одинаковы, поэтому полная вероятность ошибки равна вероятности перекрещивания переходов Р. Для вычисления Р. необходимо знать ансамбль последовательностей UИ. Иными словами, нужно указать конкретный способ кодирования. Решение вопроса об оптимальном выборе последовательностей UИ в общем случае представляет собой чрезвычайно сложную задачу, требующую отдельного рассмотрения. С целью ее упрощения будем полагать, что последовательности UИ выбираются из последовательностей U случайным образом. При этом условии вероятность того, что случайный переход от UИ к V будет перекрещиваться с другими переходами, приближенно равна отношению общего числа переходов ко всему количеству типичных последовательностей V. Следовательно, вероятность ошибки декодирования

(6.62)

Эта оценка вероятности ошибки является грубым приближением, однако она правильно указывает на характер зависимости Род от М и.

При согласовании канала с источником каждой типичной последовательности источника присваивается одна из последовательностей , поэтому их число МИвыбирается равным количеству типичных последовательностей источника. Если энтропия источника равна , то на основании (6.23) можно записать

(6.63)

Подставляя в (6.62) значения МИ, МГи N из (6.63), (6,61) и (6.60) и логарифмируя, получаем

Разделив это равенство на среднюю длительность сообщений в соответствии с (6.50), будем иметь

где

При максимальной скорости передачи сообщений по каналу и

(6.64)

Из выражения (6.62) следует, что вероятность ошибки декодирования Род может быть сколь угодно малой при неограниченном уменьшении g. Для того чтобы при этих, условиях сохранить достаточно малой величину ε, необходимо увеличивать количество сообщений п в типичных последовательностях. Что касается всех остальных нетипичных последовательностей из п сообщений, которые до сих пор не рассматривались, то их можно закодировать весьма сложными сигналами, обладающими высокой помехоустойчивостью, не заботясь о длительности таких сигналов, поскольку суммарная вероятность нетипичных последовательностей весьма кала и они не вызовут существенного уменьшения скорости передачи информации.

Таким образом, возможность одновременного установления сколь угодно малой вероятности ошибки декодирования Род и малой величины ε доказывает справедливость теоремы Шеннона.

Обратное утверждение теоремы о том, что при RИ>C декодирование со сколь угодно малой ошибкой невозможно, следует из того факта, что в этих условиях MИMГ>N и, следовательно, всегда будут иметь место перекрещивания переходов от U к V, coздающие неопределенность в установлении принадлежности V.

На первый взгляд может показаться, что поскольку вероятность ошибки в канале Р0монотонно уменьшается с увеличением длительности сигналов, то сколь угодно высокая достоверность при декодировании достигается только при неограниченном уменьшении скорости передачи. Теорема Шеннона доказывает, что наличие помех и ошибок в канале само по себе не препятствует передаче сообщений со сколь угодно малой вероятностью ошибок декодирования Род, а лишь ограничивает максимальную скорость передачи информации С. Высокая достоверность декодирования и конечная скорость передачи не исключают друг друга. В этом состоит чрезвычайно важное значение теоремы для теории и техники связи. Вместе с тем следует подчеркнуть, что из теоремы не вытекает конкретный способ наилучшего кодирования.

Применение на практике рассмотренного в теореме Шеннона общего метода, основанного на укрупнении кодируемых последовательностей, сильно усложняет кодирующие и декодирующие устройства и увеличивает задержку сигналов. Поэтому с инженерной точки зрения такой метод не эффективен. Однако теорема не утверждает, что укрупнение кодируемых сообщений является единственным способом. Поэтому в настоящее время продолжаются интенсивные поиски способов кодирования, которые бы позволяли с аппаратурой приемлемой сложности достигать предельных возможностей, указанных теоремой Шеннона.

Для обеспечения высокой достоверности передачи сообщений необходимо применять коды с избыточностью. Если R=C, то в соответствии с (6.50) средняя взаимная информация . В канале без помех она приобретает максимальное значение . Тогда коэффициент избыточности по аналогии с (6.12) равен:

(6.65)

Иными, словами, теорема утверждает, что для перелагай сообщений со сколь угодно малой вероятностью ошибки декодирования: Род могут быть найдены коды с минимальной избыточностью, равной χ. При передаче бинарных сигналов на основании (6.65), (6.33) и (6.58) минимальная избыточность равна:

(6.66)

6.8. Энтропия непрерывных сообщений

При передаче непрерывных сообщений переданные сигналы s(t) являются функциями времени, принадлежащими некоторому множеству, а принятые сигналы x(t) будут их искаженными вариантами. Все реальные сигналы имеют спектры, основная энергия которых сосредоточена в ограниченной полосе F. Согласно теореме Котельникова такие сигналы определяются своими значениями в точках отсчета, выбираемых через интервалы . В канале на сигнал накладываются помехи, вследствие чего количество различимых уровней сигнала в точках отсчета будет конечным. Следовательно, совокупность значений непрерывного сигнала эквивалентна некоторой дискретной конечной совокупности. Это позволяет нам определить необходимое количество информации и пропускную способность канала при передаче непрерывных сообщений на основании результатов, полученных для дискретных сообщений.

Определим сначала количество информации, которое содержится в одном отсчете сигнала. относительно переданного сигнала. Это можно сделать на основании соотношения (6.41), если в последнем вероятности выразить через соответствующие плотности вероятности и взять предел при

(6.67)

Среднее количество информации в одном отсчете непрерывного сигнала определяется путем усреднения выражения (6.67) по всем значениям s и x:

(6.68)

где p(s, x) — совместная плотность вероятности, а S и X — области возможных значений s и х.

Выражение (6.68) можно представить как разность

(6.69)

где

(6.70)

Величина H(s) характеризует информационные свойства сигналов и по форме записи аналогична энтропии дискретных сообщений (6.6). Так как в выражение (6.70) входит дифференциальное распределение вероятностей p(s), то H(s) называют дифференциальной энтропией сигнала s. Выражение H(s/x) представляет собой условную дифференциальную энтропию сигнала s:

(6.71) Подобно тому, как это было сделано для дискретного канала, выражение (6.68) можно записать в другой форме

(6.72)

где

(6.73)

— дифференциальная энтропия сигнала х и

(6.74)

— условная дифференциальная энтропия сигнала х, называемая также энтропией шума.

Многие свойства энтропии непрерывного распределения аналогичны свойствам энтропии дискретного распределения. Если непрерывный сигнал s ограничен интервалом то энтропия H(s) максимальна и равна log(), когда сигнал 5 имеет равномерное распределение

(6.75)

Если ограничено среднеквадратичное значение непрерывного сигнала

то энтропия, максимальная при нормальном распределении,

(6.76)

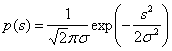
и равна:

(6.77)

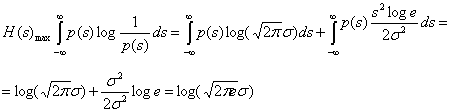
Необходимо отметить, что, в отличие от энтропии дискретных сигналов, величина дифференциальной энтропии зависит от размерности непрерывного сигнала. По этой причине она не является мерой количества информации, хотя и характеризует степень неопределенности, присущую источнику. Только разность дифференциальных энтропии (6.69) или (6.72) количественно определяет среднюю информацию

6.9. Скорость передачи и пропускная способность непрерывного канала. Формула Шеннона

Для того чтобы найти среднее количество информации T(s,x), передаваемое сигналом на интервале Т, необходимо рассмотреть n=2FT отсчетов непрерывного сигнала на входе канала: s1; s2;.., sn и на выходе канала: x1; x2;..;хп. В этом случае по аналогии с выражениями (6.69) и (6.72) можно записать

(6.78)

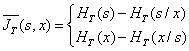
где

s, sbx, х„

Энтропии HT(s) и HT(s/x) описываются аналогичными выражениями, только всюду необходимо поменять местами переменные s и х Скорость передачи информации по непрерывному каналу находится как предел:

(6.79)

Максимальная скорость передачи в непрерывном канале определяет его пропускную способность

(6.80)

где максимум определяется по всем возможным ансамблям входных сигналов s.

Вычислим пропускную способность непрерывного канала, в котором помехой является аддитивный шум. w(t), представляющий собой случайный эргодический процесс с нормальным распределеннием и равномерным спектром. Средние мощности сигнала я шума ограничены величинами Рси Р, а ширина их спектра paвна F.

Согласно выражениям (6,80) и (6.78) имеем

(6.81)

Прежде всего найдем величину НT (x/s). С этой целью рассмотрим энтропию шума для одного отсчета (6.74), которая с учетом соотношения p(s, x)=p(s)p(x/s) может быть представлена в следующем виде:

(6.82)

При заданном значении s сигнал на выходе канала x=s+w полностью определяется аддитивным шумом w. Поэтому

(6.83)

где рш(х—s) — плотность вероятности шума.

Подставляя (6.83) в (6.82) и заменяя переменную х на , т. е. подставляя вместо х сумму s +, можем записать

Принимая во внимание, что, получим

Следовательно, условная энтропия H(x/s) при аддитивном шуме зависит только от его распределения рш(), что и объясняет термин энтропия шума. Следовательно, на интервале Т

(6.84)

где n=2FT.

Значения шума с равномерным спектром некоррелированы между собой в моменты отсчетов, разделенные интервалом

Отсутствие статистической взаимосвязи между отсчетами шума позволяет представить энтропию суммы п отсчетов шума (6.84) как сумму энтропий отдельных отсчетов, которые вследствие стационарности шума равны между собой. С учетом этих соображений можно записать

Поскольку отсчеты шума статистически независимы, а каждый из них распределен по нормальному закону, то энтропия HT(w) максимальна и в соответствии с (6.77) равна:

(6.85)

где вместо подставлено .

При данной величине HT(x/s) = HT(w) пропускная способность (6.81) отыскивается путем максимизации НТ(х). Максимум НТ(х), очевидно, имеет место, когда сигнал х так же, как и шум, характеризуется нормальным распределением и равномерным спектром.

Отсюда

(6.86)

Здесь предполагается, что сигнал s и помеха w независимы, поэтому мощность сигнала х равна сумме мощностей. Подставляя (6.85) и (6.86) в (6.81), окончательно получим

(6.87)

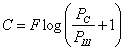
Так как х и w имеют нормальное распределение, то сигнал s=x—w также должен иметь нормальное распределение. Отсюда следует важный вывод: для того чтобы получить максимальную скорость передачи информации, необходимо применять сигналы с нормальным распределением и равномерным спектром.

Формула (6.87), впервые выведенная Шенноном, играет важную роль в теории и технике связи, Она показывает те предельные возможности, к которым следует стремиться при разработке современных систем связи. Так как при равномерном спектре мощность шума определяется произведением Pш=N0F, то ф-лу (6.87J можно записать в другом виде

(6.88)

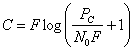
С увеличением F пропускная способность монотонно возрастает стремится, как показано на рис. 6.4а, к величине

(6.89)

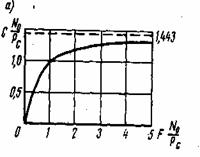
Рис. 6.4. Зависимость пропускной способности С от полосы пропускания F в непрерывном канале

Нa рис. 6.46 зависимость (6.88) изображена в другой нормировке, из которой следует, что при фиксированных значениях пропускной способности С и энергетического спектра шума N существует обратная зависимость между Рси F. Иными словами, допускается уменьшение мощности сигнала за счет расширения его спектра.

Формулу (6.87), выведенную для равномерных спектров сигнала и шума, можно распространить и на случай неравномерных спектров. С этой целью в окрестностях некоторой частоты выберем достаточно узкую полосу, в которой спектры сигнала Gc(f) и шума Gш(f) будут постоянными. Тогда для этой полосы в соответствии с (6.87) /пропускная способность будет равна:

(6.90)

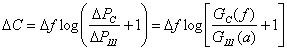
где и

Полная пропускная способность вычисляется как интеграл от (6.90) по всем частотам спектра сигнала

(6.91)

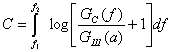
Можно показать, что при заданном спектре шума Gш(f) и ограниченной мощности сигнала максимум С имеет место в случае выполнения условия

(6.92)

т. е. мощность сигнала должна возрастать на тех частотах, где уменьшается мощность шума и наоборот. Можно также поставить вопрос: если выполняется условие (6.92), то при каком спектре шума получается минимальная пропускная способность? Оказывается, что этому условию удовлетворяет равномерный спектр, т. е. спектр белого шума. Таким образом, белый шум, уменьшающий в наибольшей степени пропускную способность, является самым опасным видом помех.

Рассмотрим теперь вопрос о производительности источника непрерывных сообщений и о влиянии на качество их передачи помех, действующих в канале связи. При отсутствии каких-либо ограничений, накладываемых на непрерывные сообщения, количество содержащейся в них информации согласно (6.1) равно бесконечности:

Поэтому источник таких сообщений обладает бесконечной производительностью (6.25). Для того чтобы количество информации и производительность источника приобрели определенный смысл и стали конечными величинами, необходимо рассматривать непрерывное сообщение u(t) с учетам точности его оценки. Последняя, в частности, определяется погрешностью приборов, с помощью которых измеряется или регистрируется непрерывное сообщение. Обычно погрешность количественно оценивается среднеквадратичным отклонением приближенного непрерывного сообщения u*(t) от его точного значения u(t):

Нетрудно понять, что чем меньше , тем большее количество информации в среднем содержится в u*(t) относительно u(t) и тем выше производительность источника.

Количество информации на выходе источника при >0 по аналогии с (6.68) определяется как

(6.93)

Для ограниченной погрешности всегда можно найти такой способ воспроизведения u(t) посредством и* (t), а следовательно, такое распределение р'(и, и*), при котором выражение (6.93) достигает наименьшего значения. Распределение р'(и, и*) является наиболее выгодным, так как оно позволяет при заданной .погрешности воспроизводить u(t), используя минимальное количество информации. Наименьшее значение J(и, и*) при называется эпсилон-энтропией

(6.94)

Тогда производительность источника непрерывных сообщений

Для непрерывного канала с пропускной способностью С, на вход которого подключается источник, обладающий производительностью , Шенноном была доказана следующая теорема.

Если при заданной погрешности оценки сообщений источника его производительность <C, то существует способ кодирования, позволяющий передавать все непрерывные сообщения источника с ошибкой в воспроизведении на выходе канала, сколь угодно мало отличающейся от .

Иначе говоря, дополнительная неточность в воспроизведении сообщения v(t) на выходе канала, обусловленная воздействием помех, может быть сделана весьма незначительной, т. е.

, где — сколь угодно малая величина.

Скорость передачи информации по каналу в конечном счете определяется скоростью потока информации на выходе приемника

где НТ(и) — энтропия принятого сообщения v(t), HT(w*) — энтропия шума на выходе приемника. Если считать, что сообщение v(t) и помеха w*(t) на выходе приемника имеют нормальное распределение и равномерный спектр, то

(6.95)

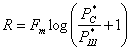
Здесь Fm — ширина спектра частот принимаемого сообщения, обычно равная полосе пропускания приемника по низкой частоте; P* — средняя мощность принятого сообщения v(t); Р* — средняя мощность шума на выходе приемника.

6.10. Пропускная способность каналов с переменными параметрами

Характеристики системы связи в значительной степени зависят от параметров канала связи, который используется для передачи сообщений. Исследуя пропускную способность каналов, мы предполагали, что их параметры сохраняются постоянными. Однако большинство реальных каналов обладают переменными параметрами. Параметры канала, как правило, изменяются во времени случайным образом. Как уже отмечалось (§ 5.7), случайные изменения коэффициента передачи канала μ вызывают замирания сигнала, что эквивалентно воздействию мультипликативной помехи. Эквивалентная мощность этой помехи согласно (5.76) равна Тогда суммарная мощность помех в канале с переменными параметрами при наличии аддитивной помехи будет равна:

Отсюда следует, что замирания сигнала приводят к увеличению мощности помех, а следовательно, и к снижению пропускной способности канала (6.87) .

Рассмотрим, каким образом вычисляется пропускная способность канала с замираниями при передаче непрерывных сообщений. В этих условиях необходимо найти такое распределение вероятностей сигнала, которое при заданных статистических свойствах коэффициента передачи μ обеспечивало бы максимальную скорость передачи информации.

Рис. 6.5. Зависимость пропускной способности от среднего отношения сигнала к помехе для каналов с постоянными параметрами (1) и рэлеевскими замираниями (2)

Решение задачи в общем виде вызывает значительные трудности. Однако в случае медленных замираний, когда скорость замираний намного меньше скорости изменения непрерывного сообщения, можно с достаточной точностью предсказывать по текущим значениям коэффициента его последующие значения. При таком допущении максимум скорости передачи по-прежнему имеет место для сообщений с нормальным распределением, что дает возможность пользоваться ф-лой (6.87). Подставляя в (6.87) мощность принимаемого сигнала ²Р0, где Р0—переданная мощность сигнала, получим пропускную способность при фиксированном :

Усреднив по всем значениям , найдем среднее значение пропускной способности канала при медленных замираниях

где p() — плотность вероятности коэффициента передачи. Во многих каналах изменения коэффициента подчиняются закону Рэлея (5.77). На рис. 6.5 показаны зависимости C/F от среднего отношения Р/Рдля канала с постоянными параметрами 1 и канала с рэлеевскими замираниями 2. Из анализа кривых рис. 6.5 следует, что медленные рэлеевеские замирания уменьшают пропускную способность канала не более чем на 17%.

Для вычисления пропускной способности дискретных каналов при быстрых замираниях могут быть использованы выражения для С, полученные при постоянных параметрах (6.58) и (6.59). В эти формулы необходимо подставить вместо вероятности ошибки ее среднюю статистическую величину, найденную путем усреднения по всем значениям коэффициента . Подставляя (5.81) в (6.58), получаем выражение для пропускной способности канала с ортогональными двоичными сигналами ири быстрых рэлеевских замираниях

Здесь — что дает возможность заменить в (6.58)

отношением

Полученное выражение для С обладает максимумом, который достигается при :

В этом случае наблюдается значительный проигрыш по сравнению с пропускной способностью аналогичного канала без замираний

В многопозиционных системах положение существенно улучшается. Если число позиций , то при рэлеевских замираниях

Это дает проигрыш всего лишь на 27% по сравнению с таким же каналом без замираний. Отсюда следует вывод, что в условиях замираний передача дискретных сообщений более эффективна при использовании многопозиционных кодов.

6.11. Эффективность систем передачи информации

Пропускная способность канала связи С определяет максимальную скорость передачи информации, т. е. является тем пределом, которого можно достичь при идеальном кодировании. Естественно, что в реальных каналах скорость передачи R всегда будет меньше С. Степень отличия R от С зависит от того, насколько рационально выбрана и эффективно используется та или иная система связи. Наиболее общей оценкой эффективности системы связи является коэффициент использования канала

(6.96)

Для дискретных систем связи можно записать, где и — эффективность системы кодирования и эффективность системы модуляции. Вводя избыточность сообщения, и избыточность сигнала , получим

(6.97)

где — полная избыточность системы.

При передаче непрерывных сообщений согласно выражениям (6.87) и (6.95) имеем

(6.98)

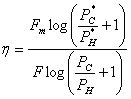
В ряде практических случаев удобными оценками эффективности связи являются коэффициент использования мощности сигнала

(6.99)

где — интенсивность помехи, и коэффициент использования полосы частот канала

(6.100)

Коэффициент является основным показателем эффективности для тех систем, о которых мощность сигнала жестко ограничена (например, для космических систем). В системах проводной связи более важным показателем является коэффициент .

Согласно выражению (6.97) для коэффициента использования канала эффективность системы связи полностью определяется величиной ее избыточности. Отсюда задача повышения эффективности связи сводится к задаче уменьшения избыточности сообщения и сигнала.

Избыточность сообщения, как мы видели, обусловлена тем, что элементы сообщения не являются равновероятными и между ними имеется статистическая связь. При кодировании можно перераспределить вероятности исходного сообщения так, чтобы распределение вероятностей символов кода приближалось к оптимальному (к равномерному в дискретном случае или к нормальному при передаче непрерывных сообщений). Такое перераспределение позволяет устранить избыточность, зависящую от распределения вероятностей элементов сообщения. Примером подобного кодирования является код ШеннонаФано, рассмотренный в § 6.5

Если перейти от кодирования отдельных символов сообщения к кодированию целых групп символов, то можно устранить взаимосвязь между ними и тем самым еще уменьшить избыточность. Общая идея такого метода кодирования, который называют методом укрупнения, состоит в следующем. Исходное сообщение разбивается на отрезки по k символов в каждом. Такие отрезки мо-гут рассматриваться как укрупненные элементы сообщения. Можно показать, что вероятностные связи между такими укрупненными элементами слабее, чем между элементами исходного сообщения. Очевидно, чем больше k (крупнее отрезки), тем слабее будет связь между ними. Далее укрупненные элементы кодируются с учетом их распределения вероятностей.

Следует заметить, что при укрупнении элементов происходит преобразование, состоящее в переходе к коду с более высоким основанием , где т— первоначальное основание.

Своеобразным примером метода укрупнения сообщений является стенографический текст. Каждый стенографический знак в этом тексте выражает целое слово или даже группу слов.

Что касается сигнала, то его избыточность зависит от способа

модуляции и от вида переносчика. Процесс модуляции обычно сопровождается расширением полосы частот сигнала по сравнению

с полосой частот передаваемого сообщения. Это расширение полосы и является избыточным. Частотная избыточность также увеличивается при переходе от синусоидального переносчика к переносчику импульсному или шумоподобному. С точки зрения повышения эффективности передачи следовало бы выбирать такие способы модуляции, которые имеют малую избыточность. К таким системам, в частности, относится однополосная передача, в которой передаваемые сигналы не содержат частотной избыточности — они являются просто копиями передаваемых сообщений.

Однако, говоря об эффективности системы связи, нельзя забывать о ее помехоустойчивости. Устранение избыточности повышает эффективность передачи, но снижает при этом достоверность (помехоустойчивость) и, наоборот, сохранение или введение избыточности позволяет обеспечить высокую достоверность передачи. Например, при телеграфной передаче текста устранение избыточности приводит к тому, что становится труднее исправлять ошибки в сообщении и в конечном счете снижается помехоустойчивость. При сохранении избыточности в тексте помехоустойчивость будет выше.

При кодировании в ряде случаев избыточность специально вводится с целью повышения достоверности передачи. Примером такого кодирования являются корректирующие коды.

Аналогичная ситуация имеет место и в отношении избыточности сигнала. Частотная избыточность гори различных видах модуляции, используется по-разному. При частотной модуляции, например, мы можем получить больший выигрыш в помехоустойчивости, чем при амплитудной модуляции, а при кодовой импульсной модуляции этот выигрыш еще больше. Частотная избыточность шумового переносчика позволяет снизить влияние замираний и сосредоточенных помех.

Следовательно, при оценке различных систем связи необходимо учитывать, по крайней мере, два показателя: эффективность и помехоустойчивость, совокупность этих двух показателей составляет достаточно полную характеристику системы.

Наиболее совершенной системой считается такая, которая обеспечивает наибольшую эффективность при заданной помехоустойчивости или, наоборот, обеспечивает наибольшую помехоустойчивость при заданной эффективности [2].

Вопросы для повторения

1. Какой критерий используется для количественной оценки информации? Почему применяется логарифмическая мера количества информации?

2. Что называется энтропией и как она определяется для источников независимых и зависимых сообщений?

3. Каковы причины появления избыточности в сообщении?

4. Какие источники сообщения называются стационарными и эргодическими?

5. Что называется пропускной способностью канала? Чему она равна для двоичного канала без помех?

6. Поясните принцип оптимального статистического кодирования.

7. Как определяется скорость передачи и пропускная способность канала с помехами?

8. Какие выводы следуют из теоремы Шеннона для дискретного канала с помехами?

9. Как определяется количество передаваемой информации в непрерывных каналах?

10. Проанализируйте формулу Шеннона для пропускной способности непрерывного канала.

11. Сформулируйте теорему Шеннона для непрерывного канала и поясните ее смысл.

12. Как вычисляется пропускная способность каналов с переменными параметрами?

13. Что называется эффективностью системы связи и как она определяется количественно?

14. Поясните зависимость между помехоустойчивостью и эффективностью связи. Приведите примеры.

Источник

Информация, данные, сигналы. Источники информации и ее носители. Количество информации и энтропия. Формулы Хартли и Шеннона.

Информация будем определять через ее основные свойства (т.к. наряду с материей и энергией она является первичным понятием нашего мира и поэтому в строгом смысле не может быть определена):

информация приносит сведения, об окружающем мире которых в рассматриваемой точке не было до ее получения;
информация не материальна и не может существовать в отрыве от формы представления информации (последовательностей сигналов или знаков — сообщений);
сообщения содержат информацию лишь для тех, кто способен ее распознать.

name=’more’>

Сообщения содержат информацию не потому, что копируют объекты реальной действительности, а по общественной договоренности о связи носителей и объектов, этим носителем обозначенных (например, слово обозначает некоторый предмет объективной действительности). Кроме того, носители могут быть сформированы естественно протекающими физическими процессами.

Для того чтобы сообщение можно было передать получателю, необходимо воспользоваться некоторым физическим процессом, способным с той или иной скоростью распространяться от источника к получателю сообщения. Изменяющийся во времени физический процесс, отражающий передаваемое сообщение называется сигналом.

Чтобы применить математические средства для изучения информации требуется отвлечься от смысла, содержания информации. Этот подход был общим для упомянутых нами исследователей, так как чистая математика оперирует с количественными соотношениями, не вдаваясь в физическую природу тех объектов, за которыми стоят соотношения. Поэтому, если смысл выхолощен из сообщений, то отправной точкой для информационной оценки события остается только множество отличных друг от друга событий и соответственно сообщений о них.

Пусть нас интересует следующая информация о состоянии некоторых объектов: в каком из четырех возможных состояний (твердое, жидкое, газообразное, плазма) находится некоторое вещество? на каком из четырех курсов техникума учится студент? Во всех этих случаях имеет место неопределенность интересующего нас события, характеризующаяся наличием выбора одной из четырех возможностей. Если в ответах на приведенные вопросы отвлечься от их смысла, то оба ответа будут нести одинаковое количество информации, так как каждый из них выделяет одно из четырех возможных состояний объекта и, следовательно, снимает одну и ту же неопределенность сообщения.

Неопределенность неотъемлема от понятия вероятности. Уменьшение неопределенности всегда связано с выбором (отбором) одного или нескольких элементов (альтернатив) из некоторой их совокупности. Такая взаимная обратимость понятий вероятности и неопределенности послужила основой для использования понятия вероятности при измерении степени неопределенность в теории информации. Если предположить, что любой из четырех ответов на вопросы равновероятен, то его вероятность во всех вопросах равна 1/4.

Одинаковая вероятность ответов в этом примере обусловливает и равную неопределенность, снимаемую ответом в каждом из двух вопросов, а значит, каждый ответ несет одинаковую информацию.

Теперь попробуем сравнить следующие два вопроса: на каком из четырех курсов техникума учится студент? Как упадет монета при подбрасывании: вверх «гербом» или «цифрой»? В первом случае возможны четыре равновероятных ответа, во втором – два. Следовательно, вероятность какого-то ответа во втором случае больше, чем в первом (1/2 > 1/4), в то время как неопределенность, снимаемая ответами, больше в первом случае. Любой из возможных ответов на первый вопрос снимает большую неопределенность, чем любой ответ на второй вопрос. Поэтому ответ на первый вопрос несет больше информации! Следовательно, чем меньше вероятность какого-либо события, тем большую неопределенность снимает сообщение о его появлении и, следовательно, тем большую информацию оно несет.

Предположим, что какое-то событие имеет mравновероятных исходов. Таким событием может быть, например, появление любого символа из алфавита, содержащего m таких символов. Как измерить количество информации, которое может быть передано при помощи такого алфавита? Это можно сделать, определив число Nвозможных сообщений, которые могут быть переданы при помощи этого алфавита. Если сообщение формируется из одного символа, то N = m, если из двух, то N = m · m = m². Если сообщение содержит n символов (n– длина сообщения), то N = mn. Казалось бы, искомая мера количества информации найдена. Ее можно понимать как меру неопределенности исхода опыта, если под опытом подразумевать случайный выбор какого-либо сообщения из некоторого числа возможных. Однако эта мера не совсем удобна.

При наличии алфавита, состоящего из одного символа, т.е. когда m = 1, возможно появление только этого символа. Следовательно, неопределенности в этом случае не существует, и появление этого символа не несет никакой информации. Между тем, значение Nпри m = 1не обращается в нуль. Для двух независимых источников сообщений (или алфавита) с N₁и N₂числом возможных сообщений общее число возможных сообщений N = N₁N₂, в то время как логичнее было бы считать, что количество информации, получаемое от двух независимых источников, должно быть не произведением, а суммой составляющих величин.

Выход из положения был найден Р. Хартли, который предложил информацию I, приходящуюся на одно сообщение, определять логарифмом общего числа возможных сообщений N:

Если же все множество возможных сообщений состоит из одного (N = m = 1), то

что соответствует отсутствию информации в этом случае. При наличии независимых источников информации с N₁ и N₂ числом возможных сообщений

I (N) = log N = log N₁N₂ = log N₁ + log N₂

т.е. количество информации, приходящееся на одно сообщение, равно сумме количеств информации, которые были бы получены от двух независимых источников, взятых порознь.

Формула, предложенная Хартли, удовлетворяет предъявленным требованиям. Поэтому ее можно использовать для измерения количества информации. Если возможность появления любого символа алфавита равновероятна (а мы до сих пор предполагали, что это именно так), то эта вероятность р= 1/m. Полагая, что N = m, получим

I = log N = log m = log (1/p) = – log p,

Полученная формула позволяет для некоторых случаев определить количество информации. Однако для практических целей необходимо задаться единицей его измерения. Для этого предположим, что информация – это устраненная неопределенность. Тогда в простейшем случае неопределенности выбор будет производиться между двумя взаимоисключающими друг друга равновероятными сообщениями, например между двумя качественными признаками: положительным и отрицательным импульсами, импульсом и паузой и т.п.

Количество информации, переданное в этом простейшем случае, наиболее удобно принять за единицу количества информации. Полученная единица количества информации, представляющая собой выбор из двух равновероятных событий, получила название двоичной единицы, или бита. (Название bitобразовано из двух начальных и последней букв английского выражения binary unit, что значит двоичная единица.)

Бит является не только единицей количества информации, но и единицей измерения степени неопределенности. При этом имеется в виду неопределенность, которая содержится в одном опыте, имеющем два равновероятных исхода. На количество информации, получаемой из сообщения, влияет фактор неожиданности его для получателя, который зависит от вероятности получения того или иного сообщения. Чем меньше эта вероятность, тем сообщение более неожиданно и, следовательно, более информативно. Сообщение, вероятность

которого высока и, соответственно, низка степень неожиданности, несет немного информации.

Р. Хартлипонимал, что сообщения имеют различную вероятность и, следовательно, неожиданность их появления для получателя неодинакова. Но, определяя количество информации, он пытался полностью исключить фактор «неожиданности». Поэтому формула Хартлипозволяет определить количество информации в сообщении только для случая, когда появление символов равновероятно и они статистически независимы. На практике эти условия

выполняются редко. При определении количества информации необходимо учитывать не только количество разнообразных сообщений, которые можно получить от источника, но и вероятность их получения.

Наиболее широкое распространение при определении среднего количества информации, которое содержится в сообщениях от источников самой разной природы, получил подход. К Шеннона.

Рассмотрим следующую ситуацию. Источник передает элементарные сигналы kразличных типов. Проследим за достаточно длинным отрезком сообщения. Пусть в нем имеется N₁сигналов первого типа, N₂сигналов второго типа, …, N_kсигналов k-го типа, причем N₁ + N₂ + … + N_k = N– общее число сигналов в наблюдаемом отрезке, f₁, f₂, …, f_k– частоты соответствующих сигналов. При возрастании длины отрезка сообщения каждая из частот стремится к фиксированному пределу, т.е.

lim f_i = p_i, (i = 1, 2, …, k),

где р_iможно считать вероятностью сигнала. Предположим, получен сигнал i-го типа с вероятностью р_i, содержащий – log p_iединиц информации. В рассматриваемом отрезке i-й сигнал встретится примерно Np_iраз (будем считать, что Nдостаточно велико), и общая информация, доставленная сигналами этого типа, будет равна произведению Np_i log р_i. То же относится к сигналам любого другого типа, поэтому полное количество информации, доставленное отрезком из Nсигналов, будет примерно равно. Чтобы определить среднее количество информации, приходящееся на один сигнал, т.е. удельную информативность источника, нужно это число разделить на N. При неограниченном росте приблизительное равенство перейдет в точное.

В результате будет получено асимптотическое соотношение – формула Шеннона. Оказалось, что формула, предложенная Хартли, представляет собой частный случай более общей формулы Шеннона.

Кроме этой формулы, Шенноном была предложена абстрактная схема связи, состоящая из пяти элементов (источника информации, передатчика, линии связи, приемника и адресата), и сформулированы теоремы о пропускной способности, помехоустойчивости, кодировании и т.д

Не позволяйте цифровому миру контролировать вас — подписывайтесь на наш канал и узнавайте, как защитить свою приватность!

Источник

Понятие информации

Информация – это одно из фундаментальных понятий современной науки, наряду с понятиями материи и энергии. По-видимому, не только понятие. В начале прошлого века Эйнштейн показал, что материя и энергия – по сути одно и то же (знаменитая формула (E=m c^2)). Современные исследования в физике указывают на то, что подобная связь может быть и между информацией и энергией.

С точки зрения же человека, информация – это некие сведения, которые могут быть понятными, достоверными, актуальными и т.п., или наоборот.

Существуют различные формальные подходы к определению информации. С точки зрения информатики, нас интересуют два определения.

Информация по Шеннону: Информация – это снятая неопределенность.

Это удобное интуитивное определение. Неопределенность в данном случае – характеристика нашего незнания о предмете. Например, в момент броска игрального кубика, мы не знаем, какая из 6 граней выпадет. Когда же кубик останавливается на какой-то грани – мы получаем информацию.

Это определение, однако, не слишком удобно без некоторой количественной меры неопределенности.

Величина неопределенности: количество возможных равновероятных исходов события

Так, например, игральный кубик имеет неопределенность 6.

Такой подход к определению информации называется содержательным. Он интуитивно понятен, однако, не отвечает на вопрос “сколько информации получено”.

Количество информации по Колмогорову: количество информации, содержащееся в сообщении, записанном в виде последовательности символов, определяется минимально возможным количеством двоичных знаков, необходимых для кодирования этого сообщения, безотносительно к его содержанию.

Поскольку любой алфавит может быть закодирован в двоичном, очевидно это определение достаточно универсально: оно применимо для любого сообщения, которое может быть записано на каком-либо языке. Этот подход называется алфавитным.

В качестве основной единицы количества информации принято брать бит – от binary digit.

При алфавитном подходе один бит – это количество информации, которое можно закодировать одним двоичным знаком (0 или 1). С точки зрения содержательного подхода, один бит – это количество информации, уменьшающее неопределенность в два раза.

Существуют более крупные единицы информации, которые чаще используются на практике.

название	размер
байт	8 бит
килобайт	(10^3) байт
мегабайт	(10^6) байт
гигабайт	(10^9) байт
терабайт	(10^{12}) байт
кибибайт	(2^{10}) байт
мебибайт	(2^{20}) байт
гибибайт	(2^{30}) байт
тебибайт	(2^{40}) байт

В вопросе хранения информации, основным показателем является не количество информации, а информационный объем

Информационный объем сообщения: количество двоичных символов, используемых для кодирования сообщения.

В отличие от количества информации, информационный объем может быть не минимальным. В частности, кодирование текстов в различных кодировках далеко не оптимально.

Формула Хартли

Сколько же информации получается в результате броска кубика?

Рассмотрим сначала более простую задачу: сколько информации получается в результате броска монеты? Считаем, что возможны два варианта: “орел” и “решка”.

Исходя из содержательного подхода, неопределенность броска монеты составляет 2. После броска, мы имеем один вариант. Следовательно, неопределенность уменьшилась вдвое. В результате броска монеты мы получаем один бит информации.

Рассмотрим теперь бросок двух монет (или два броска одной монеты). Каждый из бросков имеет два варианта исхода. Всего мы имеем четыре варианта исхода: орел-орел, орел-решка, решка-орел, решка-решка. После бросков, мы получаем один конкретный вариант, то есть, неопределенность уменьшается в 4 раза – или дважды уменьшается в 2 раза. Мы, таким образом, получаем 2 бита информации.

Для броска трех монет, имеем 8 вариантов исхода, и в результате получаем 3 бита информации.

Интуитивно ясно, что если имеется (N) равновероятных исходов, то количество информации, которое мы получаем при реализации одного из них, составляет (log_2 N). Докажем это более строго.

(Delta)

для набора из (N) различных символов можно составить (N^m) различных комбинаций (“слов”) длины (m) (это утверждение легко доказывается по индукции, и известно из комбинаторики).

Существует такое (k in mathbb{N}) – количество необходимых для кодирования этого слова двоичных знаков – что [2^k < N^m leq 2^{k+1}].

Логарифмируя неравенства, получаем: [ k < mlog_2 N leq k+1] или [ frac{k}{m} < log_2 N leq frac{k}{m}+frac{1}{m}]. Таким образом, среднее количество информации, приходящееся на один символ (frac{k}{m}) отличается от (log_2 N) не более, чем на (frac{1}{m}).

Тогда при оптимальном кодировании информации (которое при неограниченном (m) достижимо с произвольной точностью), на один символ приходится (log_2 N) бит информации (или, что то же, один символ кодируется в среднем (log_2 N) двоичными символами) (blacksquare)

Выражение [H = log_2 N,] где (H) – количество информации в символе (N)-значного алфавита, называется Формулой Хартли.

Возвращаясь к кубику, количество информации, полученное в результате броска кубика составляет (log_2 6 approx 2.585).

Применения формулы Хартли

Формула Хартли находит много различных применений. Одно из наиболее интересных заключается в оценке классов сложности вычислительных задач. Рассмотрим на примере алгоритмов сортировки.

С точки зрения теории информации, сортировка представляет собой выбор из всех возможных перестановок массива одной такой, которая удовлетворяет критерию сортировки.

Массив длинны (N) имеет (N!) различных перестановок (это утверждение легко доказывается по индукции, и известно из комбинаторики).

Операция сравнения двух элементов по сути несет один бит информации (либо первый больше второго, либо меньше или равен), а по формуле Хартли количество информации, соответствующее выбору одного из (N!) вариантов (H=log_2(N!)), то есть, потребуется по крайней мере (log_2(N!)) операций сравнения.

Для больших (N) можно использовать формулу Стирлинга для оценки факториала: [N! = sqrt{2pi N} N^N e^{-N}.]

Тогда [begin{align}
H
&approx log_2(sqrt{2pi N} N^N e^{-N})
\ & = log_2(sqrt{2pi N}) + log_2(N^N) + log_2(e^{-N})
\ & = frac{1}{2} log_2(2 pi N) + N log_2(N) -N log_2(e)
\ & = frac{1}{2} log_2(2 pi) + (N+frac{1}{2}) log_2(N) — N log_2(e)
end{align}]

Поскольку (N log_2 N) растет быстрее, чем (N), то по порядку роста можно ввести оценку [H = mathcal{O}(N log N),] что будет соответствовать классу сложности DTIME((Nlog N)).

Таким образом, в частности, алгоритм сортировки слиянием по порядку роста близок к теоретически оптимальному.

Закон аддитивности информации

Еще одно занимательное следствие формулы Хартли – это аддитивность информации.

Рассмотрим некую пару ((x_1, x_2) in X), где (x_1in X_1) и (x_2 in X_2). Очевидно, что (X = X_1 times X_2) – декатрово произведение, и, если (X_1) состоит из (N_1) элементов, а (X_2) – из (N_2) элементов, то (X) состоит из (N_1 N_2) элементов.

По формуле Хартли, количество информации, соответствующее выбору ((x_1, x_2)) из (X) равно [H(x_1, x_2) = log_2(N_1 N_2)]

По правилом арифметики с логарифмами,

[begin{align}
H(x_1, x_2)
& = log_2(N_1 N_2)
\ & = log_2 N_1 + log_2 N_2
end{align}]

Но (log_2 N_1) в свою очередь равно количеству информации, соответствующему выбору (x_1) из (X_1), а (log_2 N_2) – (x_2) из (X_2). И действительно, чтобы выбрать пару ((x_1, x_2)), мы можем выбрать сначала (x_1), затем (x_2).

Таким образом, по формуле Хартли, [H(x_1, x_2) = H(x_1) + H(x_2),] то есть, информация аддитивна – если мы получаем (H_1) информации об одном предмете и (H_2) – о другом, то всего мы получаем (H_1 + H_2) информации о двух предметах.

Закон аддитивности информации: количество информации, необходимое для установления пары равно суммарному количеству информации, необходимому для независимого установления элементов пары.

Этот закон легко обобщается для набора (N) элементов.

Формула Шеннона

До сих пор мы рассматривали случай, когда все варианты равновероятны. Предположим, что это не так.

Пусть у нас имеется сообщение (“слово”), состоящее из символов ({a, b}), причем известно, что в сообщении есть (n) символов (a) и (m) символов (b). Сколько информации приходится в среднем на символ этого сообщения?

Рассмотрим новый алфавит ({a_1, ldots, a_n, b_1, ldots, b_m}) из (n+m) символов и запишем с его помощью наше сообщение таким образом, чтобы символы не повторялись. В таком случае, вероятность обнаружить какой-либо символ одинакова, и мы можем применить формулу Хартли.

Среднее количество информации на символ в таком случае, [H_{n+m} = log_2(n+m)]. Однако, в исходном алфавите, мы не различаем символы (a_i). Если бы мы делали различие между ними, то выбор одного из (n) вариантов соответствовал бы количеству информации (H_{a_i} = log_2 n). Аналогично, (H_{b_i} = log_2 m). Однако, поскольку мы не делаем различий, мы по сути теряем эту информацию для каждого символа.

Всего на сообщение теряется (n log_2 n + m log_2 m) бит информации, а всего информации в сообщении ((n+m) log_2(n+m)).

Таким образом, всего в сообщении в исходном алфавите содержится [begin{align}
H_Sigma
& = (n+m) log_2(n+m) — n log_2 n — m log_2 m
\ & = n log_2(n+m) + m log_2(n+m) — n log_2 n — m log_2 m
\ & = n log_2frac{n+m}{n} + m log_2frac{n+m}{m}
end{align}] бит информации.

Тогда среднее количество информации на один символ сообщения

[ H = frac{H_Sigma}{n+m} ] [ H = frac{n}{n+m} log_2frac{n+m}{n} + frac{m}{n+m}log_2frac{n+m}{m} ]

Но (P_a = frac{n}{n+m}) – это вероятность обнаружить в сообщении символ (a), а (P_b = frac{m}{n+m}) – символ (b). Тогда

[ H = P_a log_2frac{1}{P_a} + P_b log_2frac{1}{P_b} ]

Это частный случай формулы Шеннона – для двух-символьного алфавита.

Интересным оказывается то, что количество информации на один символ алфавита зависит от вероятности обнаружить этот символ.

Поскольку вероятность аддитивна, (P_a + P_b = 1), (P_b = 1 — P_a), можем записать (H) как функцию (P_a):

[ H(P_a) = P_a log_2frac{1}{P_a} + (1-P_a) log_2frac{1}{1-P_a} ]

График этой функции показан на рисунке:

Можно так же рассчитать производную:

[frac{d H(P_a)}{dP_a} = log_2frac{1-P_a}{P_a}]

и найти нули:

[log_2frac{1-P_a}{P_a} = 0] [frac{1-P_a}{P_a} = 1] [1-P_a = P_a] [P_a = frac{1}{2}]

Получается, что количество информации, получаемое в результате выбора одного элемента из двух, максимально при равных вероятностях и составляет 1 бит.

В других случаях, выбор из двух вариантов соответствует менее чем одному биту информации.

Формула Шеннона для двух-символьного алфавита легко обобщается на случай (N)-символьного алфавита по индукции: [ H = sum_{i=1}^N P_i log_2{frac{1}{P_i}}]

(Delta)

Действительно, база индукции для случая (N=2) уже доказана. Предположив, что формула верна для алфавита (N-1) элементов, вычислим (H) для (N) элементов.

Для этого, отождествим последние два символа алфавита. Для отождествленного алфавита количество информации на символ [ H_{N-1} = sum_{i=1}^{N-2} P_i log_2{frac{1}{P_i}} + (P_{N-1}+P_N) log_2{frac{1}{P_{N-1}+P_N}} ]

Среди двух отождествленных символов, каждый из них появляется с относительной вероятностью, соответственно, [q_{N-1} = frac{P_{N-1}}{P_{N-1}+P_N},] [q_{N} = frac{P_{N}}{P_{N-1}+P_N}.]

В силу отождествления, на каждый отождествленный символ теряется [ q_{N-1} log_2frac{1}{q_{N-1}} + q_{N} log_2frac{1}{q_{N}}] бит информации, а их доля среди всех символов составляет (P_{N-1}+P_N).

Тогда в результате отождествления, мы потеряли в среднем [ P_{N-1} log_2frac{1}{q_{N-1}} + P_{N} log_2frac{1}{q_{N}}] бит на символ. Прибавив это выражение к (H_{N-1}), получим: [ sum_{i=1}^{N-2} P_i log_2{frac{1}{P_i}} + (P_{N-1}+P_N) log_2{frac{1}{P_{N-1}+P_N}} + P_{N-1} log_2frac{1}{q_{N-1}} + P_{N} log_2frac{1}{q_{N}}] [ sum_{i=1}^{N-2} P_i log_2{frac{1}{P_i}} + P_{N-1} log_2frac{1}{q_{N-1}(P_{N-1}+P_N)} + P_{N} log_2frac{1}{q_{N}(P_{N-1}+P_N)}] [ sum_{i=1}^{N-2} P_i log_2{frac{1}{P_i}} + P_{N-1} log_2frac{1}{P_{N-1}} + P_{N} log_2frac{1}{P_{N}}] [ sum_{i=1}^{N} P_i log_2{frac{1}{P_i}}.] (blacksquare)

Связь формул Хартли и Шеннона

Формула Хартли представляет собой частный случай формулы Шеннона.

Действительно, в предположении, что имеется набор из (N) элементов, и вероятность выбора каждого элемента одинакова, то (P_i = P_j = P) и (sum_{i=1}^N P_i = 1), следовательно, (P = frac{1}{N}). Тогда по формуле Шеннона, [begin{align}
H & = sum_{i=1}^{N} P log_2{frac{1}{P}}
\ & = sum_{i=1}^{N} frac{1}{N} log_2{N}
\ & = log_2{N}.
end{align}]

Мы получили формулу Хартли.

Оптимальное кодирование информации

Для достижения соответствия информационного объема и количества информации, необходимо оптимальное кодирование информации.

Легко можно показать случаи не оптимального кодирования информации. Допустим, кодируется результат падения монеты: орел или решка. Мы уже знаем, что количество информации в данном случае равно одному биту. При этом, если закодировать эти значения, например, русскими словами в коде UTF-8, то в среднем на одно значение уйдет 9 бит.

Одним из достаточно эффективных и при этом универсальных алгоритмов является алгоритм кодирования Хаффмана.

Алгоритм Хаффмана

Алгоритм Хаффмана является алгоритмом префиксного кодирования: символы произвольного алфавита кодируются двоичными последовательностями различной длины таким образом, что ни один более короткий код не является префиксом более длинного. При этом, для достижения оптимального кодирования, наиболее часто встречающиеся символы кодируются наиболее короткой последовательностью, а наиболее редко встречающиеся – наиболее длинной.

Для построения кода, всем символам алфавита присваиваются значения приоритетов, соответствующие частоте появления символа.

Затем два символа с наименьшим значением приоритета “склеиваются”, образуя при этом бинарное дерево (выбор символов с одинаковым приоритетом произволен). Результат получает приоритет, равный сумме приоритетов входящих в него символов. Процесс продолжается, пока в итоге не останется одно бинарное дерево.

После этого, “левым” ветвям дерева (с более низким приоритетом) присваивается код “0”, а “правым” (с более высоким) – “1”. Кодом символа является последовательность кодов ветвей, приводящих к нему.

Например, нам нужно оптимально закодировать сообщение “шла Маша по шоссе”. Всего сообщение состоит из 17 символов. Символы алфавита и их приоритеты:

Символ	Приоритет
» «	4
“ш”	3
“a”	2
“о”	2
“с”	2
“л”	1
“M”	1
“п”	1
“е”	1

“Склеим” символы “п”, “е”:

Символ	Приоритет
» «	4
“ш”	3
“a”	2
“о”	2
“с”	2
(“е”, “п”)	2
“л”	1
“M”	1

Теперь “л” и “м”

Символ	Приоритет
» «	4
“ш”	3
“a”	2
“о”	2
“с”	2
(“е”, “п”)	2
(“М”, “л”)	2

Теперь “пе” и “лМ”:

Символ	Приоритет
» «	4
((“М”, “л”), (“е”, “п”))	4
“ш”	3
“a”	2
“о”	2
“с”	2

Действуя далее аналогично:

Символ	Приоритет
» «	4
((“М”, “л”), (“е”, “п”))	4
(“с”, “о”)	4
“ш”	3
“a”	2

Символ	Приоритет
(“a”, “ш”)	5
» «	4
((“М”, “л”), (“е”, “п”))	4
(“с”, “о”)	4

Символ	Приоритет
((“с”, “о”), ((“М”, “л”), (“е”, “п”)))	8
(“a”, “ш”)	5
» «	4

Символ	Приоритет
(“ ”, (“a”, “ш”))	9
((“с”, “о”), ((“М”, “л”), (“е”, “п”)))	8

Символ	Приоритет
(((“с”, “о”), ((“М”, “л”), (“е”, “п”))), (“ ”, (“a”, “ш”)))	17

Приоритет последнего оставшегося узла равен длине сообщения.

Изображение соответствующего дерева:

Таким образом, коды символов:

Символ	Приоритет	Код
» «	4	10
“ш”	3	111
“a”	2	110
“о”	2	001
“с”	2	000
“л”	1	0101
“M”	1	0100
“п”	1	0111
“е”	1	0110

Средний информационный вес символа по формуле Шеннона: [ H = 4frac{1}{17}log_2 17 + 3 frac{2}{17}log_2 frac{17}{2} + frac{3}{17}log_2 frac{17}{3} + frac{4}{17}log_2 frac{17}{4}] [ H approx 2.98 ]

Средний информационный вес по расчету:

[ H = frac{2cdot 4 + 3 cdot 3 + 3cdot 2cdot 3 + 4cdot 4}{17} = 3 ]

Разница оценки по формуле Шеннона и фактической величины не превосходит [frac{1}{17} approx 0.06]

С ростом общего числа символов в сообщении это различие будет становиться все меньше.

Минимальная сложность сортировки сравнением

Анализ сложности сортировки сравнением можно провести с точки зрения теории информации. Действительно, сравнение типа a < b даёт результат “да” или “нет”, то есть не больше 1 бита информации. В то же время, сортировка массива (N) различных элементов соответствует выбору одной из всех возможных перестановок. Число перестановок массива длины (N) – (N!). Тогда, считая все перестановки равновероятными, по формуле Хартли получаем, что выбору одной перестановки соответствует (log_2 N!) бит информации.

Рассмотрим (log_2 N!):

[log_2 N! = sum_{i=1}^N log_2 i < N log_2 N] [log_2 N! = sum_{i=1}^N log_2 i > sum_{i=N/2}^N log_2 i > frac{N}{2} log_2 frac{N}{2}]

Пусть (Nge 4), тогда:
(log_2 N ge log_2 4 = 2)
(log_2 frac{N}{2}ge 1)
(frac{N}{4}log_2 frac{N}{2}ge frac{N}{4})
(frac{N}{2}log_2 frac{N}{2} ge frac{N}{4}log_2 N,)
тогда [N log_2 N > log_2 N! > frac{N}{4}log_2 N,]

т.е. для выбора одной перестановки, в отсутствие дополнительной информации о структуре массива, требуется (mathcal O(Nlog N)) бит, т.е. (mathcal O(Nlog N)) операций сравнения.

Таким образом, для алгоритмов, выполняющих одно сравнение за итерацию, число итераций не может быть лучше (mathcal O(Nlog N).)

Источник

Комбинаторный подход: информация по Хартли

Пример

Применение: цена информации

Вероятностный подход: энтропия Шеннона

Примеры

Свойства энтропии Шеннона

Энтропия пары

Примеры

Свойства энтропии Шеннона пары случайных величин

Условная энтропия Шеннона

Примеры

Свойства условной энтропии

Взаимная информация

Примеры

Свойства взаимной информации

Применение энтропии Шеннона: кодирование

Связь с энтропией

Применение энтропии Шеннона: шифрования с закрытым ключом

Алгоритмический подход: колмогоровская сложность

Сравнение языков программирования

Свойства колмогоровской сложности

Примеры

Несжимаемые строки

Колмогоровская сложность: вычислимость

Связь с энтропией Шеннона

Применение колмогоровской сложности: бесконечность множества простых чисел

Применение колмогоровской сложности: алгоритмическая случайность

Свойства случайных последовательностей

Заключение

Определение количества информации по к. Шеннону

Энтропия сообщения. Среднее количество информации по всем состояниям системы:

6.1. Мера количества информации

6.2. Энтропия источника дискретных сообщений

6.3. Статистические свойства источников сообщений

6.4. Скорость передачи информации и пропускная способность дискретного канала без помех

6.5. Оптимальное статистическое кодирование сообщений

6.7. Теорема Шеннона для дискретного канала с помехами

6.8. Энтропия непрерывных сообщений

6.9. Скорость передачи и пропускная способность непрерывного канала. Формула Шеннона

6.10. Пропускная способность каналов с переменными параметрами

6.11. Эффективность систем передачи информации

Вопросы для повторения

Понятие информации

Формула Хартли

Применения формулы Хартли

Закон аддитивности информации

Формула Шеннона

Связь формул Хартли и Шеннона

Оптимальное кодирование информации

Алгоритм Хаффмана

Минимальная сложность сортировки сравнением

Не пропустите также: