Как найти среднее давление газа - Avtoru.top - решение различных проблем

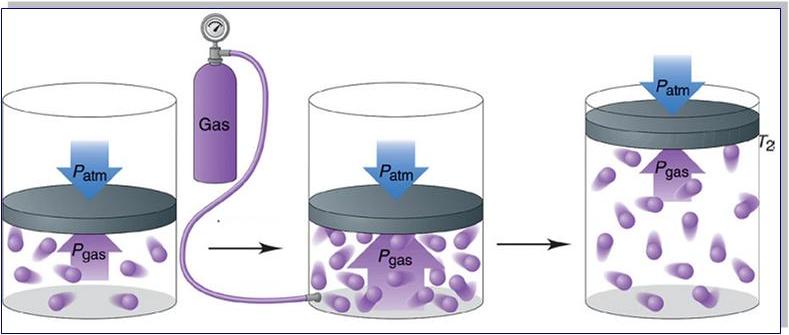
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.

Идеальные газы

Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.

В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.

В идеальном газе существует лишь единственный вид взаимодействия — упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.

Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.

Причина возникновения давления в газах

Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.

Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:

P = F/S

Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:

F*Δt = Δp

Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 10²³), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.

Формула давления газа идеального из молекулярно-кинетической теории

При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.

Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.

Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:

P = N*m*v²/(3*V)

Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.

Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:

P*V = n*R*T

Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.

Из уравнения выше легко получить формулу давления газа:

P = n*R*T/V

Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.

Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.

Давление в газовой смеси

Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.

Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:

Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.

Пример задачи

Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.

Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:

P = N*m*v²/(3*V)

Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:

m = M/N_A;

n = N/N_A;

m*N = M*n;

P = M*n*v²/(3*V)

Объем сосуда в кубических метрах равен 0,01 м³. Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.

Источник

При
эксплуатации газопроводов возникает
необходимость определения среднего
давления в газопроводе, например, для
оценки количества газа в трубопроводе.
Для определения среднего давления
часто используется средняя интегральная
по длине газопровода величина, т. е.

;

Интегрируя,
получаем

С
другой стороны, среднее давление можно
определить как среднее арифметическое
р_сра=(р_н+р_к)/2.

Введение
среднего арифметического значения
равносильно замене параболического
закона изменения давления линейным.
Погрешность при вычислении р_ср
равна

Если
ввести значение r=р_н/р_к,
то

При
r=1,5

=1,32
%. Эта погрешность лежит в пределах
погрешности манометров для измерения
давления. Это позволяет допустить, что
при значениях r<1,5
для оценочных технологических расчетов
р_ср
можно принимать средним арифметическим.

2.5.6. Расчет газопровода высокого давления при равномерном отборе газа по длине.

Представим
отдельный участок газовой сети с отборами
газа по его длине как газопровод, через
который и последующие за ним участки
транспортируется транзитный расход
газа М_Т,
а на самом участке отбирается путевой
отбор газа М_П
(рис. 2.10.). При большом числе отборов газа
подобный газопровод можно представить
с достаточной точностью как газопровод
с равномерным по длине отбором газа
m=М_П/
,
где

— длина участка. Тогда пропускная
способность газопровода будет по длине
переменной, уменьшающейся от начала
газопровода. В начале газопровода
М_Н=М_Т+М_П
в конце газопровода М_К=М_Т,
в любой точке по длине газопровода при
отчете от конца газопровода М_х=М_Т+mx.

Рис.2.10
Расчетная
схема газопровода с распределенным
отбором

В
проектах при гидравлических расчетах
газопроводов, которые можно отнести к
газопроводам с распределенным
отбором,

считают как один участок
газопровода без отборов газа с постоянным
по длине расчетным расходом газа. При
этом расчетный расход газа выражают
в виде М_Р=М_Т+
М_П,
где

— коэффициент, учитывающий влияние на
перепад давления соотношения между
транзитным и путевым отборами газа. При
введении расчетного расхода газа перепад
давлении будет одним и тем же: как у
газопровода с множеством отборов газа
и переменной пропускной способностью,
так и у эквивалентного газопровода без
отборов газа, но с введением расчетного
расхода газа: М_Р=М_Т+
М_П.
В этом случае эквивалентный газопровод
рассчитывается по известной формуле

Для
газопровода с переменным отбором газа
имеем

Преобразуя,
получаем

Интегрируя,
в пределах от р_н
до р_к
и
от 0 до

,
имеем

Для
эквивалентного газопровода величина
в скобках должна быть приравнена к
значению

.
Из соотношения

найдем величину

.
Сокращая и преобразуя, получаем:

откуда

При
М_Т=
0

0,577;
при М_Т/М_П=1

0,52;
при М_Т/М_П=10

0,505 и т.д.

Величина

колеблется от

= 0,577 при отсутствии транзита через
участок газопровода до

0,5
при больших соотношениях М_Т/М_П.

Таким
образом, зная начальное давление в
газопроводе, величины транзитного
и путевого расхода газа и

,
определяют конечное давление по
формуле для газопровода без отборов
газа. Данный подход резко ускоряет
расчет газопроводов с большим количеством
отборов газа но длине. Заметим, что
режимы газовых приборов задаются
индивидуально, так как входные давления
у них будут разные. Определяющим давлением
является давление в конце газопровода.
Если оно соответствует необходимому
для конечного газового прибора, то все
остальные работают с повышенным
давлением на входе.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
#
#
#
#
30.03.20151.74 Mб24конспект лекций по начертательной геометрии.pdf

Источник

Уравнение состояния идеального газа

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: модель идеального газа, связь между давлением и средней кинетической энергией теплового движения молекул идеального газа, связь температуры газа со средней кинетической энергией его частиц, уравнение , уравнение Менделеева—Клапейрона.

Из трёх агрегатных состояний вещества наиболее простым для изучения является газообразное. В достаточно разреженных газах расстояния между молекулами намного больше размеров самих молекул (тогда как в жидкостях и твёрдых телах молекулы «упакованы» весьма плотно).Поэтому силы взаимодействия между молекулами таких газов очень малы.

Для описания разреженных газов в физике используется модель идеального газа. В рамках этой модели делаются следующие допущения.

1. Пренебрегаем размерами молекул. Иными словами, молекулы газа считаются материальными точками.
2. Пренебрегаем взаимодействием молекул на расстоянии.
3. Соударения молекул друг с другом и со стенками сосуда считаем абсолютно упругими.

Таким образом, идеальный газ — это газ, частицы которого являются не взаимодействующими на расстоянии материальными точками и испытывают абсолютно упругие соударения друг с другом и со стенками сосуда.

Средняя кинетическая энергия частиц газа

Оказывается, что ключевую роль в описании идеального газа играет средняя кинетическая энергия его частиц.

Частицы газа двигаются с разными скоростями. Пусть в газе содержится частиц, скорости которых равны . Масса каждой частицы равна m_0 . Кинетические энергии частиц:

$E_1=frac{displaystyle m_0 v_1^2}{displaystyle 2 vphantom{1^a}}, E_2=frac{displaystyle m_0 v_2^2 }{displaystyle 2 vphantom{1^a}}, ldots,E_N=frac{displaystyle m_0 v_N^2}{displaystyle 2 vphantom{1^a}}.$

Средняя кинетическая энергия частиц газа это среднее арифметическое их кинетических энергий:

$E=frac{displaystyle E_1+E_2+ ldots+E_N}{displaystyle N vphantom{1^a}}= frac{displaystyle 1}{displaystyle N vphantom{1^a}}left ( frac{displaystyle m_0 v_1^2}{displaystyle 2 vphantom{1^a}}+frac{displaystyle m_0 v_2^2}{displaystyle 2 vphantom{1^a}}+ ldots + frac{displaystyle m_0 v_N^2}{displaystyle 2 vphantom{1^a}} right ) =frac{displaystyle m_0}{displaystyle 2 vphantom{1^a}} frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}.$

Последний множитель — это средний квадрат скорости, обозначаемый просто v_2 :

$v_2=frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}.$

Тогда формула для средней кинетической энергии приобретает привычный вид:

$E=frac{displaystyle m_0 v^2}{displaystyle 2 vphantom{1^a}}.$ (1)

Корень из среднего квадрата скорости называется средней квадратической скоростью:

$v=sqrt{ frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}}.$

Основное уравнение МКТ идеального газа

Cвязь между давлением газа и средней кинетической энергией его частиц называется основным уравнением молекулярно-кинетической теории идеального газа. Эта связь выводится из законов механики и имеет вид:

$p= frac{displaystyle 2}{displaystyle 3 vphantom{1^a}} nE.$ (2)

где — концентрация газа (число частиц в единице объёма). С учётом (1) имеем также:

$p= frac{displaystyle 1}{displaystyle 3 vphantom{1^a}} m_0 nv^2.$ (3)

Что такое m_0n ? Произведение массы частицы на число частиц в единице объёма даёт массу единицы объёма, то есть плотность: . Получаем третью разновидность основного уравнения:

$p= frac{displaystyle 1}{displaystyle 3 vphantom{1^a}} rho v^2.$ (4)

Энергия частиц и температура газа

Можно показать, что при установлении теплового равновесия между двумя газами выравниваются средние кинетические энергии их частиц. Но мы знаем, что при этом становятся равны и температуры газов. Следовательно, температура газа — это мера средней кинетической энергии его частиц.

Собственно, ничто не мешает попросту отождествить эти величины и сказать, что температура газа — это средняя кинетическая энергия его молекул. В продвинутых курсах теоретической физики так и поступают. Определённая таким образом температура измеряется в энергетических единицах — джоулях.

Но для практических задач удобнее иметь дело с привычными кельвинами. Связь средней кинетической энергии частиц и абсолютной температуры газа даётся формулой:

$E= frac{displaystyle 3}{displaystyle 2 vphantom{1^a}} kT,$ (5)

где $k=1,38 cdot 10^{-23}$ Дж/К — постоянная Больцмана.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Уравнение состояния идеального газа» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Совет 1: Как вычислить давление газа

Для решения некоторых физических задач бывает нужно рассчитывать давление газа . При этом в задаче может упоминаться как окаймляющий воздух и пары вещества, так и газ, тот, что находится в сосуде. Как именно вычислить давление газа , зависит от того, какие параметры заданы в задаче.

Вам понадобится

– формулы для расчета давления газа.

Инструкция

1. Обнаружьте давление безукоризненного газа при наличии значений средней скорости молекул, массы одной молекулы и концентрации вещества по формуле P=?nm0v2, где n – насыщенность (в граммах либо молях на литр), m0 – масса одной молекулы.

2. Если в условии дана плотность газа и средняя скорость его молекул, рассчитайте давление по формуле P=??v2, где ? — плотность в кг/м3.

3. Вычислите давление , если вы знаете температуру газа и его концентрацию, применяя формулу P=nkT, где k – непрерывная Больцмана (k=1,38·10-23 моль·К-1), Т — температура по безусловной шкале Кельвина.

4. Обнаружьте давление из 2-х равноценных вариантов уравнения Менделеева-Клайперона в зависимости от знаменитых значений: P=mRT/MV либо P=?RT/V, где R – универсальная газовая непрерывная (R=8,31 Дж/моль·К), ? — число вещества в молях, V – объем газа в м3.

5. Если в условии задачи указана средняя кинетическая энергия молекул газа и его насыщенность, обнаружьте давление с подмогой формулы P=?nEк, где Eк — кинетическая энергия в Дж.

6. Обнаружьте давление из газовых законов — изохорного (V=const) и изотермического (T=const), если дано давление в одном из состояний. При изохорном процессе отношение давлений в 2-х состояниях равно отношению температур: P1/P2=T1/T2. Во втором случае, если температура остается непрерывной величиной, произведение давления газа на его объем в первом состоянии равно тому же произведению во втором состоянии: P1·V1=P2·V2. Выразите незнакомую величину.

7. Рассчитайте давление из формулы внутренней энергии безукоризненного одноатомного газа : U=3·P·V/2, где U – внутренняя энергия в Дж. Отсель давление будет равняться: P=?·U/V.

8. При расчете парциального давления пара в воздухе, если в условии даны температура и относительная влажность воздуха, выразите давление из формулы ?/100=Р1/Р2, где ?/100 — относительная влажность, Р1 — парциальное давление водяного пара, Р2 — наивысшее значение паров воды при данной температуре. В ходе расчета пользуйтесь таблицами зависимости максимальной упругости пара (максимального парциального давления) от температуры в градусах Цельсия.

Совет 2: Как вычислить давление

Даже приложив малое усилие, дозволено сделать существенное давление . Все, что для этого нужно – сосредоточить это усилие на маленький площади. И напротив, если равномерно распределить по крупной площади существенное усилие, давление получится относительно малым. Дабы узнать, каким именно, придется провести расчет.

Инструкция

1. Переведите все начальные данные в единицы системы СИ: силу – в ньютоны, массу – в килограммы, площадь – в квадратные метры и т.п. Тогда давление позже расчета будет выражено в паскалях.

2. В случае если в задаче приведена не сила, а масса груза, вычислите силу по дальнейшей формуле:F=mg, где F – сила (Н), m – масса (кг), g – убыстрение свободного падения, равное 9,80665 м/с?.

3. Если в условиях взамен площади указаны геометрические параметры области, на которую оказывается давление , сначала рассчитайте площадь этой области. Скажем, для прямоугольника:S=ab, где S – площадь (м?), a – длина (м), b – ширина (м).Для круга:S=?R?, где S – площадь (м?), ? – число «пи», 3,1415926535 (безразмерная величина), R – радиус (м).

4. Дабы узнать давление , поделите усилие на площадь:P=F/S, где P – давление (Па), F – сила (н), S – площадь (м?).

5. При необходимости переведите давление в производные единицы: килопаскали (1 кПа=1000 Па) либо мегапаскали (1 МПа=1000000 Па).

6. Для перевода давления из паскалей в атмосферы либо миллиметры ртутного столба воспользуйтесь следующими соотношениями: 1 атм=101325 Па=760 мм рт. ст.

7. В ходе подготовки сопроводительной документации к товарам, предуготовленным для поставки на экспорт, может понадобиться выразить давление в фунтах на квадратный дюйм (PSI – pounds per square inch). В этом случае руководствуйтесь дальнейшим соотношением: 1 PSI=6894,75729 Па.

Видео по теме

Совет 3: Как рассчитать давление в сосуде

Выдержит ли ведро, если налить в него воды? А если налить туда больше тяжелую жидкость? Для того дабы ответить на данный вопрос, нужно рассчитать давление , которое оказывает жидкость на стенки того либо другого сосуда. Это дюже зачастую бывает нужно на производстве – скажем, при изготовлении цистерн либо резервуаров. Исключительно главно рассчитать крепкость емкостей, если речь идет об опасных жидкостях.

Вам понадобится

Сосуд
Жидкость с вестимой плотностью
Знание закона Паскаля
Ареометр либо пикнометр
Мерная мензурка
Весы
Таблица поправок для взвешивания на воздухе
Линейка

Инструкция

1. Определите плотность жидкости. Обыкновенно это делается с поддержкой пикнометра либо ареометра. Ареометр наружно схож на обыкновенный термометр, внизу его размещен резервуар, заполненный дробью либо ртутью, в средней части – термометр, а в верхней части – шкала плотностей. Всякое деление соответствует относительной плотности жидкости. Там же указывается температура, при которой надобно измерять плотность. Как водится, измерения проводят при температуре 20оС. Сухой ареометр погружают в сосуд с жидкостью, пока не станет ясно, что он там вольно плавает. Подержите ареометр в жидкости 4 минуты и посмотрите, на ярусе какого деления он погружен в воду.

2. Измерьте высоту яруса жидкости в сосуде любым доступным методом. Это может быть линейка, штанген-циркуль, мерный циркуль и т.д. Нулевая отметка линейки должна находиться на нижнем ярусе жидкости, верхняя – на ярусе поверхности жидкости.

3. Вычислите давление на дно сосуда. Согласно закону Паскаля, оно не зависит от формы самого сосуда. Давление определяется только плотностью жидкости и высотой ее яруса, и рассчитывается по формуле P= h*?, где P – давление , h – высота яруса жидкости, ? – плотность жидкости. Приведите единицы измерения в вид, комфортный для последующего использования.

Видео по теме

Обратите внимание!
Класснее пользоваться комплектом ареометров, в тот, что входят приборы для измерения плотности жидкостей легче либо тяжелее воды. Существуют особые ареометры для измерения плотности спирта, молока и некоторых других жидкостей. Дабы измерить плотность жидкости ареометром, сосуд должен быть не менее 0,5 л. Если рассматривать жидкость как несжимаемую, то давление на все поверхности сосуда будет равномерным.

Полезный совет
Измерение плотность с подмогой пикнометра больше точное, правда и больше трудоемкое. Вам потребуются еще аналитические весы, дистиллированная вода, спирт, эфир и термостат. Такое измерение проводят в основном в намеренно оснащенных лабораториях. Взвесьте прибор на аналитических весах, которые дают высокую точность (до 0,0002 г). Заполните его дистиллированной водой, чуть выше расположения метки, и закройте пробкой. Разместите пикнометр в термостат и вынесете 20 минут при температуре 20оС. Уменьшите число воды до метки. Излишки уберите пипеткой и вновь закройте пикнометр. Разместите его в термостат на 10 минут, проверьте, совпадает ли ярус жидкости с меткой. Протрите пикнометр снаружи мягкой салфеткой и оставьте на 10 минут за стеклом коробки аналитических весов, позже чего вновь взвесьте. Узнав таким образом точную массу прибора, вылейте из него воду, сполосните спиртом и эфиром, продуйте. Заполните пикнометр жидкостью, плотность которой надобно узнать, и действуйте верно так же, как и с дистиллированной водой. Если нет особого прибора, дозволено измерить плотность с подмогой весов и мерной мензурки. Поставьте на весы мензурку и уравновесьте чашечки. Запишите массу. Наполните мензурку исследуемой жидкостью на заданную единицу объема и вновь взвесьте. Разница в массах является массой жидкости в заданном объеме. Поделив массу на объем, вы получите плотность.

Совет 4: Как вычислить среднюю скорость

Вычислить среднюю скорость несложно. Для этого нужно легко поделить длину пройденного пути на время. Впрочем на практике и при решении задач изредка появляются добавочные вопросы. Скажем, что считать пройденным путем? Показания спидометра либо настоящее смещение объекта? Что считать временем в пути, если объект половину времени никуда не двигался? Без контроля всех этих нюансов нереально положительно вычислить среднюю скорость.

Вам понадобится

калькулятор либо компьютер, спидометр

Инструкция

1. Для вычисления средней скорости равномерного движения объекта, легко измерьте его скорость в всякий точке пути. Потому что скорость движения непрерывна, то она и будет средней скоростью.Еще проще эта связанность выглядит в виде формулы:Vср=V, гдеVср – средняя скорость, аV – скорость равномерного движения.

2. Дабы вычислить среднюю скорость равноускоренного движения, обнаружьте среднее арифметическое исходной и финальной скорости. Для этого обнаружьте сумму этих скоростей и поделите на два. Полученное число и будет средней скоростью объекта.Нагляднее это выглядит в виде дальнейшей формулы:Vср = (Vкон + Vнач) / 2, гдеVср – средняя скорость,Vкон – финальная скорость,Vнач – исходная скорость.

3. Если задана величина убыстрения и исходная скорость, а финальная скорость неведома, то преобразуйте вышеприведенную формулу дальнейшим образом:Потому что при равноускоренном движении Vкон = Vнач + a*t, где а – убыстрение объекта, а t – время, то имеем:Vср = (Vкон + Vнач) / 2 = (Vнач + a*t + Vнач) / 2 = Vнач + a*t / 2

4. Если же, напротив, знамениты финальная скорость и убыстрение тела, но исходная скорость не задана, то преобразуйте формулу к дальнейшему виду:Vср = (Vкон + Vнач) / 2 = (Vкон + Vкон – a*t) / 2 = Vкон – a*t / 2

5. Если заданы длина пройденного телом пути, а также время, которое потребовалось на прохождение этого расстояния, то примитивно поделите данный путь на затраченное время. То есть используйте всеобщую формулу:Vср = S / t, где S – всеобщая длина пройденного пути.Время, затраченное на прохождение пути учитывается самостоятельно от того, двигался объект постоянно либо останавливался.

6. Если в условиях задачи намеренно не указано, какую именно среднюю скорость нужно вычислить, то подразумевается средняя путевая скорость.Дабы вычислить среднюю путевую скорость, берется всеобщая длина пройденного пути, т.е. его траектория. Если во время движения объект возвращался в пройденные точки пути, то это расстояние также учитывается. Так, скажем, для автомобиля длина пути, нужная для вычисления средней путевой скорости, будет соответствовать показаниям спидометра (разности показаний).

7. Если нужно вычислить среднюю скорость перемещения (смещения), то под пройденным путем подразумевается то расстояние, на которое тело подлинно переместилось.Потому что перемещение неизменно происходит в определенном направлении, то смещение (S) величина векторная, т.е. характеризуется как направлением, так и безусловной величиной. Следственно, и значение средней скорости смещения будет величиной векторной. В связи с этим, при решении сходственных задач неукоснительно узнайте: какую именно скорость требуется вычислить. Среднюю путевую скорость, числовое значение средней скорости смещения либо вектор средней скорости смещения.В частности, если тело в процессе движения возвращается в начальную точку, то считается, что его средняя скорость смещения равна нулю.

Совет 5: Как обнаружить давление совершенного газа

Безупречным считают газ, в котором взаимодействие между молекулами пренебрежимо немного. Помимо давления, состояние газа характеризуется температурой и объемом. Соотношения между этими параметрами отображены в газовых законах.

Инструкция

1. Давление газа прямо пропорционально его температуре, числу вещества, и обратно пропорционально объему сосуда, занимаемого газом. Показателем пропорциональности служит универсальная газовая непрерывная R, примерно равная 8,314. Она измеряется в джоулях, поделенных на моль и на кельвин.

2. Это расположение формирует математическую связанность P=?RT/V, где ? – число вещества (моль), R=8,314 – универсальная газовая непрерывная (Дж/моль•К), T – температура газа, V – объем. Давление выражается в паскалях. Его дозволено выразить и в атмосферах, при этом 1 атм = 101,325 кПа.

3. Рассмотренная связанность – следствие из уравнения Менделеева-Клапейрона PV=(m/M)•RT. Тут m – масса газа (г), M – его молярная масса (г/моль), а дробь m/M дает в результате число вещества ?, либо число молей. Уравнение Менделеева-Клапейрона объективно для всех газов, которые возможно считать совершенными. Это капитальный физико-химический газовый закон.

4. Отслеживая за поведением совершенного газа, говорят о так называемых типичных условиях – условиях окружающей среды, с которыми особенно зачастую доводится иметь дело в реальности. Так, типичные данные (н.у.) полагают температуру в 0 градусов Цельсия (либо 273,15 градусов по шкале Кельвина) и давление в 101,325 кПа (1 атм). Обнаружено значение, чему равен объем одного моля безукоризненного газа при таких условиях: Vm=22,413 л/моль. Данный объем назван молярным. Молярный объем – одна из основных химических констант, применяемых в решении задач.

5. Значимо понимать, что при непрерывном давлении и температуре объем газа также не меняется. Данный восхитительный постулат сформулирован в законе Авогадро, тот, что заявляет, что объем газа прямо пропорционален числу молей.

Видео по теме

Полезный совет
Используйте барометр-анероид либо ртутный барометр для больше точного значения, если вам нужно вычислить давление газа в ходе эксперимента либо лабораторной работы. Для измерения давления газа в сосуде либо баллоне пользуйтесь обыкновенным либо электронным манометром.

Источник

Содержание:

Определение и формула давления
Среднее давление
Давление идеального газа
Гидростатическое давление
Единицы измерения давления
Примеры решения задач

Определение и формула давления

Определение

Давление – это физическая величина,характеризующая состояние сплошной среды. Оно равно пределу отношения нормальной составляющей силы,
которая действует на участок поверхности тела площади
$Delta S$ к размеру данной площади при
$Delta S rightarrow 0$ . Обозначается давление буквой p. Тогда математической
записью определения давления станет формула:

$$p=lim _{Delta S rightarrow 0} frac{Delta F_{n}}{Delta S}=frac{d F_{n}}{d S}$$

Выражение (1) определяет давление в точке.

Среднее давление

Средним давлением на поверхность называют величину:

$$langle prangle=frac{F_{n}}{S}(2)$$

где F_n – нормальная составляющая силы, которая действует на рассматриваемую поверхность, S – площадь этой поверхности.

Давление идеального газа

Давление идеального газа вычисляют, используя основное уравнение молекулярно – кинетической теории:

$$p=n k T(3)$$

где $n=frac{N}{V}$– концентрация молекул газа
(N – число частиц), k=1,38•10^-23 Дж/К – постоянная Больцмана, T – абсолютная температура газа.

Гидростатическое давление

Гидростатическое давление – давление внутри столба жидкости или газа, находится по формуле:

$$p=p_{0}+rho g h(4)$$

где $rho$ – плотность вещества, g=9,8 м/с² –
ускорение свободного падения, h- высота столба вещества. p₀ – внешнее давление на газ или жидкость.

Искривление поверхностного слоя жидкости ведет к возникновению дополнительного давления на жидкость, тогда давление под искривленной
жидкостью определяется как:

$$p=p_{0}^{*}+2 sigma H(5)$$

где $mathrm{P}_{0}^{*}$ –поверхностное натяжение жидкости,p₀^* – давление под не искривлённым слоем жидкости,
H — средняя кривизна поверхности жидкости, вычисляемая по закону Лапласа:

$$H=frac{1}{2}left(frac{1}{R_{1}}+frac{1}{R_{2}}right)$$

R₁, R₂ – главные радиусы кривизны.

Единицы измерения давления

Основной единицей измерения давления в системе СИ является: [p]=Па (паскаль)

Внесистемные единицы давления: [p]=мм рт.ст.(миллиметр ртутного столба),мм в.ст (мм водяного столба),атмосфера,бар.

Па= Н/м² и 1 бар=10⁵ Па.

Техническая атмосфера ~1 бар. Физическая атмосфера 1,01 бар=760 мм рт.ст.. 1 мм рт.ст.=133 Па.

Примеры решения задач

Пример

Задание. Каково давление в море на глубине h=8,5 м, если атмосферное давление равно
p₀=10⁵ Па, плотность морской воды равна
$rho$=1,03•10³ кг/м³

Решение. Основой для решения задачи служит выражение:

$$p=p_{0}+rho g h(1.1)$$

Все данные в задаче указаны в системе СИ, поэтому можно провести вычисления:

$p=10^{5}+1,03 cdot 10^{3} cdot 9,8 cdot 8,5=1,88 cdot 10^{5}$ (Па).

Ответ. $p=1,88 cdot 10^{5}$ (Па)

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

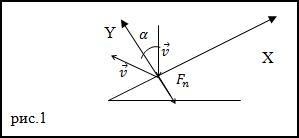
Пример

Задание. Каково давление струи на неподвижную плоскость, если струя воды ударяет ее под углом
$alpha$ к нормали
плоскости, и упруго отскакивает от нее без изменения скорости? Скорость струи v.

Решение. Сделаем рисунок.

За время $Delta t$ о стенку ударяется масса воды равная:

$$m=l S rho=v Delta t S rho$$

где S — поперечное сечение струи, $rho$ – плотность воды. В соответствии с законом сохранения импульса имеем:

$$F Delta t=m Delta v rightarrow F=frac{m Delta v}{Delta t}(2.2)$$

где F – сила, с которой вода действует на стенку.

Примем за положительное направление нормали внешней к опоре и учитывая, что струя отскакивает от стены без потери скорости, получаем:

$$Delta v=v_{2} cos alpha-left(-v_{1} cos alpharight)=v_{2} cos alpha+v_{1} cos alpha=2 v cos alpha(2.3)$$

Подставим $Delta v$ из (2.3) в выражение (2.2), учтем выражение (2.1) имеем:

$$F=frac{m 2 v cos alpha}{Delta t}=frac{v Delta t S rho 2 v cos alpha}{Delta t}=2 operatorname{Sov}^{2} cos alpha(2.4)$$

В таком случае искомое давление струи на стенку будет равно:

$$p=frac{F_{n}}{S}=2 rho v^{2}$$

Ответ. $p=2 rho v^{2}$

Читать дальше: Формула закона Ома.

Источник

Идеальные газы

Причина возникновения давления в газах

Формула давления газа идеального из молекулярно-кинетической теории

Формула давления из уравнения состояния

Давление в газовой смеси

Пример задачи

2.5.6. Расчет газопровода высокого давления при равномерном отборе газа по длине.

Уравнение состояния идеального газа

Средняя кинетическая энергия частиц газа

Основное уравнение МКТ идеального газа

Энергия частиц и температура газа

Совет 1: Как вычислить давление газа

Инструкция

Совет 2: Как вычислить давление

Инструкция

Совет 3: Как рассчитать давление в сосуде

Инструкция

Совет 4: Как вычислить среднюю скорость

Инструкция

Совет 5: Как обнаружить давление совершенного газа

Инструкция

Определение и формула давления

Среднее давление

Давление идеального газа

Гидростатическое давление

Единицы измерения давления

Примеры решения задач

Не пропустите также: