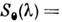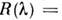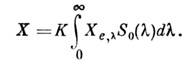-
. Общая и спектральная чувствительность фотоэлементов. Чувствительность и точность колориметрических определений.
Фотоэлементы
принято сравнивать по их чувствительности.
Чем больший фототок
дает элемент, тем он чувствительней.
Чувствительность
фотоэлементов
измеряют в микроамперах на единицу
светового потока в один люмен.
Различают
два вида чувствительности: общую
(интегральную) и спектральную
(цветовую). Общая
чувствительность определяется
по отношению
к свету, излучаемому обыкновенными
электрическими лампами накаливания
с вольфрамовой нитью, которые дают почти
белый свет с небольшим
содержанием инфракрасного.
В
таком свете нет ультрафиолетовых лучей,
которые поглощаются стеклом колбы. За
стандартный источник света принято
считать лампу, нить которой имеет
температуру 2850К.
Спектральная
чувствительность — это
чувствительность фотоэлемента
к свету различных длин волн.
Спектральную чувствительность
индивидуальных фотоэлементов изображают
графически, откладывая по оси координат
величину фототока, а по оси абсцисс —
длину волны света. Для
измерения интенсивности светового
потока применяют следующие типы
фотоэлементов:
-
Вентильные
фотоэлементы, основанные на так
называемом «фронтальном» фотоэффекте
(фотоэлементы с запирающим слоем). -
Фотосопротивления,
основанные на внутреннем сопротивлении. -
Вакуумные
или газонаполненные (фотоэлементы
с внешним фотоэффектом).
При
работе с фотоэлементами следует всегда
иметь в виду ряд факторов, влияющих на
получение точных и воспроизводимых
результатов. Во-первых, спектральная
и интегральная чувствительность
фотоэлементов может со временем
меняться, то есть наблюдается «старение»
фотоэлементов, что требует
необходимость их периодической замены.
Во-вторых, для фотоэлементов
характерно явление «утомления»
(уменьшения силы фототока), которое
наблюдается при длительном непрерывном
освещении фотоэлемента достаточно
ярким светом. Поэтому во время работы
фотоэлементу необходим «отдых».В-третьих,
чувствительность фотоэлемента бывает
неодинаковой по всей его
поверхности, поэтому большое значение
следует уделять настройке осветителя,
чтобы при параллельных измерениях
всегда освещался один и тот же
участок фотоэлемента, площадь этого
участка должна быть примерно равной 1
см2.
Равномерность освещения может быть
достигнута путем применения
матовых рассеивателей.В-четвертых,
следует отметить, что на точность
фотоэлектроколориметрических
измерений существенно влияет качество
гальванометра,
с помощью которого измеряют силу
фототока. Главное требование к
гальванометру — его сопротивление должно
быть возможно малым
и не должно превышать внутреннего
сопротивления фотоэлемента.
ВНИМАНИЕ!
Подавать свет на фотоэлементы можно
лишь в момент измерения,
всё остальное время фотоэлементы должны
быть прикрыты светонепропускающими
шторками!
-
Что такое фотоэффект, каковы его разновидности? Основные законы фототока.
Фотоэффектом
называется
отрыв электронов
от атомов различных веществ под влиянием
световой энергии.
Если
поместить две металлические пластины
в стеклянный баллон (рис.
3), из которого выкачан воздух, и включить
их электрическую цепь, то в темноте
гальванометр
покажет отсутствие тока в цепи, а при
освещении поверхности
катода светом гальванометр покажет
появление тока. Это объясняется тем,
что при освещении катода происходит
электронная
эмиссия, то
есть испускание электронов с его
поверхности.
Под
действием электростатистического поля
электроны будут двигаться к аноду и
цепь окажется
замкнутой.
Способность
металлов испускать электроны со своей
поверхности
под действием света называется
внешним
фотоэлектрическим эффектом.
При
освещении веществ, являющихся изоляторами
и полупроводниками, электроны не
могут
покинуть поверхность вещества, но они
получают
энергию, достаточную для отрыва
атомов
и передвижения их внутри вещества.
Возрастание
проводимости изоляторов и полупроводников
при освещении их светом называется
внутренним
фотоэффектом.
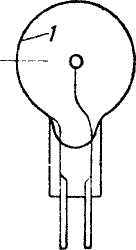
Рис. 3. Фотоэлемент
с внешним фотоэффектом
Основными законами
фотоэффекта являются закон Эйнштейна
и закон
Столетова.
Закон
Эйнштейна:
максимальная
энергия фотоэлектронов линейно
возрастает с частотой падающего
света и не зависит от интенсивности
облучения.
Закон
Столетова: Фотоэлектрический
ток прямопропорционален падающему
лучистому потоку (1888 г.).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
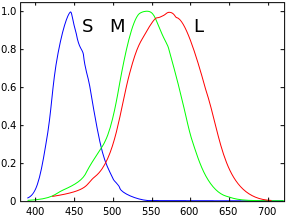
Spectral sensitivities (normalized responsivity spectra) of human cone cells, S, M, and L types
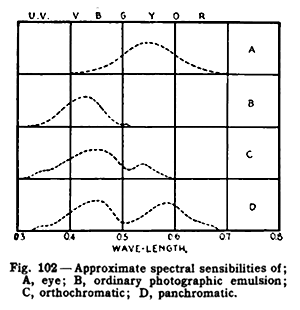
1916 plot of «spectral sensibilities.» The author also uses the more modern term «spectral sensitivity» in the same book.[1]
Spectral sensitivity is the relative efficiency of detection, of light or other signal, as a function of the frequency or wavelength of the signal.
In visual neuroscience, spectral sensitivity is used to describe the different characteristics of the photopigments in the rod cells and cone cells in the retina of the eye. It is known that the rod cells are more suited to scotopic vision and cone cells to photopic vision, and that they differ in their sensitivity to different wavelengths of light.[2][3] It has been established that the maximum spectral sensitivity of the human eye under daylight conditions is at a wavelength of 555 nm, while at night the peak shifts to 507 nm.[4]
In photography, film and sensors are often described in terms of their spectral sensitivity, to supplement their characteristic curves that describe their responsivity.[5] A database of camera spectral sensitivity is created and its space analyzed.[6] For X-ray films, the spectral sensitivity is chosen to be appropriate to the phosphors that respond to X-rays, rather than being related to human vision.[7]
In sensor systems, where the output is easily quantified, the responsivity can be extended to be wavelength dependent, incorporating the spectral sensitivity. When the sensor system is linear, its spectral sensitivity and spectral responsivity can both be decomposed with similar basis functions.[8] When a system’s responsivity is a fixed monotonic nonlinear function, that nonlinearity can be estimated and corrected for, to determine the spectral sensitivity from spectral input–output data via standard linear methods.[9]
The responses of the rod and cone cells of the retina, however, have a very context-dependent (coupled) nonlinear response, which complicates the analysis of their spectral sensitivities from experimental data.[10] In spite of these complexities, however, the conversion of light energy spectra to the effective stimulus, the excitation of the photopigment, is quite linear, and linear characterizations such as spectral sensitivity are therefore quite useful in describing many properties of color vision.[11]
Spectral sensitivity is sometimes expressed as a quantum efficiency, that is, as probability of getting a quantum reaction, such as a captured electron, to a quantum of light, as a function of wavelength.[12] In other contexts, the spectral sensitivity is expressed as the relative response per light energy, rather than per quantum, normalized to a peak value of 1, and a quantum efficiency is used to calibrate the sensitivity at that peak wavelength.[13] In some linear applications, the spectral sensitivity may be expressed as a spectral responsivity, with units such as amperes per watt.[14][15][16]
See also[edit]
- Frequency response
- Orthochromasia
References[edit]
- ^ Matthew Luckiesh (1916). Light and shade and their applications. D. Van Nostrand Company. p. 95.
spectral sensitivity luckiesh.
- ^ Michael Levine (2000). Fundamentals of Sensation and Perception (3rd ed.). Oxford University Press.
- ^ Steven H. Schwartz (2004). Visual Perception: A Clinical Orientation. McGraw-Hill Professional. ISBN 0-07-141187-9.
- ^ Gross, Herbert; Blechinger, Fritz; Achtner, Bertram (2008). Gross, Herbert H. (ed.). Handbook of optical systems. Vol. 4. Weinheim, Germany: WILEY-VCH. p. 40. ISBN 978-3-527-40380-6.
- ^ Michael Langford (1998). Advanced Photography. Focal Press. ISBN 0-240-51486-6.
- ^ Jun Jiang; Dengyu Liu; Jinwei Gu & Sabine Süsstrunk (2013). What is the space of spectral sensitivity functions for digital color cameras?. IEEE. ISBN 978-1-4673-5053-2.
- ^ John Ball & Tony Price (1995). Chesneys’ Radiographic Imaging. Blackwell Publishing. ISBN 0-632-03901-9.
- ^ Glenn E. Healey; Steven A. Shafer & Lawrence B. Wolff (1992). Physics-Based Vision. A. K. Peters Ltd. ISBN 0-86720-295-5.
- ^ Steven K. Shevell (2003). The Science of Color. Elsevier. ISBN 0-444-51251-9.
- ^ S. N. Archer (1999). Adaptive mechanisms in the ecology of vision. Springer. ISBN 0-7923-5319-6.
- ^ Arne Valberg (1995). Light Vision Color. John Wiley and Sons. ISBN 0-470-84902-9.
- ^ M. H. F. Wilkinson & F. Schut (1998). Digital Image Analysis of Microbes: Imaging, Morphometry, Fluorometry and Motility Techniques and Applications. John Wiley and Sons. ISBN 0-471-97440-4.
- ^ Peter G. J. Barten (1999). Contrast Sensitivity of the Human Eye and Its Effects on Image Quality. SPIE Press. ISBN 0-8194-3496-5.
- ^ Matt Young (1993). Optics and lasers: including fibers and optical waveguides. Springer. ISBN 3-540-65741-X.
- ^ Stephen A. Dyer (2001). Survey of Instrumentation and Measurement. Wiley-IEEE. ISBN 0-471-39484-X.
- ^ Robert B. Northrop (2004). Analysis and Application of Analog Electronic Circuits to Biomedical Instrumentation. CRC Press. ISBN 0-8493-2143-3.
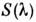
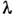
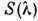
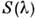
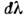
Понятие С. ч. применяется также к нелинейным приёмникам оптич. излученияи даже к биол. объектам, реакция к-рых на оптич. излучение не описываетсяколичеств. мерой. В фотобиологии С. ч. обычно наз. спектром действия. Длянелинейных приёмников С. ч.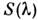
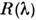
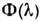
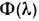
Понятие не зависящей от уровня облучения или реакции относительной С. <ч.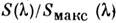
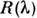
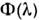
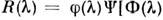
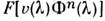
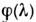
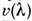
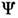
В фотобиологии понятие «спектр действия» считают тождественным понятию«С. ч.», определённому как при одинаковом заданном уровне реакции приёмника, <так и при пост. значениях квазимонохроматич. потоков оптич. излучения. <Ясно, что форма кривой спектра действия может существенно зависеть от указанныхспособов определения и изменяться при варьировании заданного уровня и условийнаблюдения реакции. Спектр действия оптич. излучения на зрит. систему человеканаз. спектральной световой эффективностью монохроматич. излучения.
Существующие измерит. модели оптич. излучения в фотобиол. процессахпостроены по принципу одного или неск. линейных спектрально аддитивныхприёмников излучения. К таким моделям, в первую очередь, относятся стандартизованныеМКО и МКМВ световые величины и колориметрич. системы (см. Колориметрия). Приэтом под линейностью понимается прямая пропорциональность реакции приёмникамощности (потоку) или энергии падающего оптич. излучения. Под спектральнойаддитивностью понимается арифметич. суммирование реакций, вызываемых излучениемразличных узких спектральных интервалов. В общем виде матем. модель линейногоспектрально аддитивного приёмника выражается соотношением для редуциров. <величин:
Здесь К — переводной множитель от единиц энерге-тич. величинк единицам, принятым в данной системе редуциров. величин;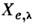
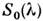
Эквивалентные 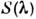
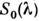
Лит.: Сапожников Р. А., Теоретическая фотометрия, 3 изд., М.,1977; Дойников А. С., Прикладная фотометрия, в кн.: Итоги науки и техники, <сер. Светотехника и инфракрасная техника, т. 5, М., 1983. А. С. Дойников.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1988.