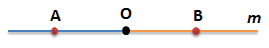Как найти совпадающий луч

Объясните, пожалуйста, что означает «Совпадающие лучи»?

Ответ:

1. Совпадающие лучи — это лучи с общим началом, расположенные на одной и той же прямой и направленные в одну и ту же сторону (но не являющиеся продолжением друг друга).

2. AB, AC — совпадающие лучи. Также BA и BC.

3. Продолжением луча CA называется луч CB.

рассмотри ∆АОВ и∆СОД

Дано:
ΔАВС — прямоугольный
∠С = 90°
∠А = 45°
АВ = 9
Найти : S aвc — ?
Решение.
Сумма острых углов прямоугольного треугольника равна 90°
∠А + ∠В = 90 ⇒ ∠В = 90 — ∠А ⇒ ∠В = 90 — 45 = 45°
∠А = ∠В = 45° ⇒ Δ АВС — равнобедренный ⇒ АС=СВ=х
По теореме Пифагора:
АС² + СВ² = АВ² ⇒ 2х² = АВ² ⇒ 2x² = 9² ⇒ x² = 81/2 = 40,5
Площадь ΔАВС :
Saвc = ¹/₂ * АВ * СВ ⇒ Sавс = 0,5х² ⇒ Saвc = 0,5 * 40,5 = 20,25

Источник

Что такое луч: определение, обозначение, признаки совпадения

В данной публикации мы рассмотрим, что из себя представляет луч (полупрямая), как обозначается, а также перечислим признаки совпадения двух лучей.

Определение луча

Луч – это часть прямой, которая имеет начало, но не конец. Иногда называется полупрямой. Обозначается двумя способами:

• Маленькой латинской буквой (a, b, c и т.д.)
• Двумя большими латинскими буквами, которые соответствуют точкам на луче, причем одна из них является его началом, и ее буква пишется первой (на рисунке ниже – AB).

Если поставить точку на прямой (в нашем случае – O), то от нее будут исходить два бесконечно продолжающихся в противоположные стороны луча (полупрямые).

Признаки совпадения лучей

Два луча совпадают, если они (должны одновременно выполняться все три условия):

1. берут начало в одной и той же точке;
2. направлены в одинаковую сторону;
3. принадлежат одной и той же прямой.

Пример:

На этом рисунке:

• Лучи AB и AC совпадают;
• Лучи BA и BC не совпадают.

Источник

Точка, линия, прямая, луч, отрезок, ломанная | Математика (геометрия)

— это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

точка A, точка B, точка C

точка 1, точка 2, точка 3

— это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Обозначается строчными (маленькими) латинскими буквами

линия a, линия b, линия c

Линия может быть

1. , если её начало и конец находятся в одной точке,
2. , если её начало и конец не соединены

замкнутые линии

разомкнутые линии

самопересекающиеся линии

линии без самопересечений

прямые линии

ломанные линии

кривые линии

— это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны

Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой

прямая линия a

прямая линия AB

Прямые могут быть

1. , если имеют общую точку. Две прямые могут пересекаться только в одной точке.
   • , если пересекаются под прямым углом (90°).
2. , если не пересекаются, не имеют общей точки.

параллельные линии

пересекающиеся линии

перпендикулярные линии

— это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону

У луча света на картинке начальной точкой является солнце

солнышко

Точка разделяет прямую на две части — два луча

Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче

луч a

луч AB

Лучи совпадают, если

1. расположены на одной и той же прямой,
2. начинаются в одной точке,
3. направлены в одну сторону

лучи AB и AC совпадают

лучи CB и CA совпадают

— это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. — это расстояние между его начальной и конечной точками

Через одну точку можно провести любое число линий, в том числе прямых

На этой странице находится ответ на вопрос Совпадающие и дополнительные лучи?, из категории
Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть
другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов
подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью
соответствующий критериям вашего поиска, можно найти с помощью простого
интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе.
Обратите внимание на варианты ответов других пользователей, которые можно не
только просмотреть, но и прокомментировать.

Что такое луч в математике

Не секрет, что знания, которые вы получили в школьные годы не всегда остаются с вами впоследствии Иногда бывает полезно изучить новое или освежить в памяти то, что вы давно забыли. Сегодня вы вспомните такое понятие как луч.

Луч — геометрическое понятие

Луч — это такая прямая линия, один из концов которой ограничен точкой, а другой продолжается до бесконечности. Таким образом, фигура тянется вперёд без ограничений. но только с одной стороны. Вторая сторона не может тянуться дальше точки, которая является началом фигуры.

На картинке вы можете посмотреть, что такое луч и как он выглядит:

Луч отмечается посредством строчной латинской буквы или двух таких точек, которые обозначены заглавными буквами латинского алфавита.

Если вы увидите отрезок с двумя точками и продолжите его в одну из сторон, как показано на рисунке, то получится луч.

Отличия луча от прямой и от отрезка

В геометрии есть три схожих понятия, которые подразумевают под собой черту — это луч, отрезок, прямая. Эти фигуры всегда изображаются без изгибов и имеют ряд особенностей.

В рамках курса математики луч — это полупрямая. Дело в том, что с одного конца он обладает признаком бесконечности, который присущ прямой линии.

В начальной точке луч имеет сходство с отрезком, так как он так же ограничен точкой.

Обратите внимание — быстро отличить фигуры друг от друга вы можете по наличию у них начала и конца:

• отрезок имеет начальную и конечную точки;
• луч — только начало;
• прямая — не располагает начальной и конечной точками.

Взаимное расположение лучей

Если на прямой линии вы поставите точку, то на ней сформируются два таких луча, начало которых находится в одной точке.

На рисунке начало для лучей — общая точка A.

По взаимному расположению лучи делятся на пересекающиеся и непересекающиеся.

Параллельный луч — это фигура, у которой любая точка находится на одинаковом расстоянии от соответствующей точки другого луча. Параллельные лучи не могут пересекаться.

Дополнительные лучи — это фигуры, которые обладают такими признаками, как:

• имеют совпадающее начало в одной точке;
• располагаются на одной прямой линии;
• направляются в разные стороны, то есть угол между ними составляет 180 градусов.

Можно ли сравнить два луча?

Луч — это такая фигура, которую нельзя измерить. Он продолжается без ограничений, поэтому не обладает характеристикой длины.

Так как невозможно измерить несколько лучей, сравнить их вы тоже не сможете.

Луч — альтернативные значения слова

Русский язык достаточно сложен и необычайно многообразен, поэтому многие слова имеют несколько разных значений, а разнообразные сочетания способны радикально менять смысл слов, которые являются их составными частями.

Сможете ли вы сходу ответить на вопрос: «Что такое луч света?». Это словосочетание употребляется нами с детства, но не так легко выразить, что оно означает.

Такая фраза описывает прямую линию, по которой направляется световая энергия. Эта энергия исходит от разных источников:

В быту вы можете услышать словосочетание «луч света в тёмном царстве». Такие слова означают — среди негативных явлений присутствует что-то хорошее. Короткое слово всегда ассоциируется с чем-то светлым, добрым и положительным.

Фраза «луч надежды» указывает, что среди множества нежелательных последствий существует не высокая вероятность благополучного исхода.

Плоскость, прямая линия, луч

Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.

Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.

Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.

Плоскость нельзя измерять, потому что она бесконечная.

Плоскость нельзя согнуть, в каком бы положении она ни находилась.

Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.

Прямая линия

Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.

Даже когда мы рисуем на листе бумаги небольшой кусок прямой линии, то мы предполагаем , что этот лист бумаги – это бесконечная плоскость, и мы можем мысленно раздвинуть видимые границы бумаги и продлить прямую бесконечно долго.

Обозначение прямой

В основном прямую, как и любую другую линию, обозначают при помощи строчной (маленькой) буквы латинского алфавита .

Иногда обозначение прямой линии происходит при помощи двух точек , которые принадлежат (часто говорят просто – лежат на) этой прямой. В этом случае ее обозначают названием этих двух точек.

Например, на рисунке 1 обозначены такие прямые:

Рис. 1 Обозначение прямой линии

Если на одной прямой лежат три и более известных нам точек, то обозначить эту линию можно любой из комбинаций имен любых двух точек .

Рис. 2 Обозначение прямой с несколькими точками

На рисунке 2 видно, что на одной прямой b лежат четыре точки: D , G , H , O . Поэтому данную прямую мы можем назвать любым из этих семи имен: b , DG , DH , DO , GH , GO или HO .

Некоторые свойства прямой

Две точки, лежащие на одной прямой, создают отрезок этой прямой.

Через две любые точки на плоскости можно провести единственную прямую.

Рис. 3 Отрезок на прямой

Две разные прямые могут пересекаться или не пересекаться.

Две прямые пересекаются в том случае, если у них есть общая точка.

И наоборот, если у двух разных прямых нет общей точки, тогда эти прямые не пересекаются .

Рис. 5 Пересечение прямых

На рисунке 5 можно видеть, что прямые l и q пересекаются в точке O , а прямые q и g не пересекаются.

Обозначение пересечения письменно записывается при помощи символа ∩: l ∩ q — прямая l пересекается с прямой q .

Как вам уже известно из этого урока, на рисунках мы можем отображать только часть прямых (поскольку они бесконечные), и что их можно мысленно увеличивать, делать более протяженными. Поэтому, если мысленно продлить прямые l и g , то станет понятно, что они тоже пересекаются.

Взаимное расположение точек и прямой , а также их обозначение, точно такое же, как и у всех линий вообще.

Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.

Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.

Рис. 6 Деление прямой линии точкой

На рисунке 1 точка O делит прямую a на две части, то есть, на два луча. Один из них, как вы видите, длится бесконечно вправо, а другой – бесконечно влево. Оба они начинаются в одной и той же точке O , которую называют началом луча.

У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.

Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.

Обозначение луча

Луч, как и прямую, обозначают двумя способами.

Рис. 7 Обозначение луча

На рисунке 2 приведены примеры обозначения луча:

• a – строчной (маленькая) буква латинского алфавита;
• OF – точками, расположенными на луче. При этом на первом месте всегда пишут точку начала луча, а на втором – любую точку, которая принадлежит лучу.

Луч имеет второе название – полупрямая.

Два луча, которые лежат на одной прямой, начинаются в одной точке и направлены в разные стороны, называются дополнительными друг другу лучами , поскольку в соединенном виде они формируют одну прямую линию в точке их начала.

Если лучи лежат на одной прямой, начинаются в одной точке и направлены в одну сторону, их называют совпадающие , или говорят, что эти лучи совпадают .

Рис. 8 Дополнительные друг другу и совпадающие лучи

На рисунке 8 видно, что:

• CB и CH – дополнительные друг другу лучи,
• BC и BH – совпадающие лучи,
• HC и HB – совпадающие лучи.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.7 / 5. Количество оценок: 23

Луч математика в треугольнике

Луч — это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой. Луч также называется полупрямой.

Любой луч имеет начало и направление. Начало луча, начальная точка или вершина луча — это точка, из которой исходит луч. Таким образом, у луча есть начало, но нет конца.

Рассмотрим три луча с общим началом:

Все 3 луча имеют общую начальную точку O, но разные направления. Про каждый из них можно сказать: луч исходит из точки O или луч исходящий из точки O .

Дополнительные лучи

Любая точка, лежащая на прямой линии, делит эту прямую на две полупрямые, то есть на две части. Каждая из этих частей будет называться дополнительным лучом относительно второго луча:

Дополнительные лучи — это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой. Также можно сказать, что дополнительными называются лучи, дополняющие друг друга до прямой линии.

Обозначение лучей

Луч обозначают одной строчной латинской буквой:

Также луч можно обозначить двумя точками, лежащими на нём:

При обозначении луча двумя точками, на первом месте ставится буква, обозначающая начало луча, а на втором — буква, обозначающая какую-либо другую его точку: луч BC.

Посмотрим на следующий пример:

Луч с началом в точке A можно обозначить как AB или AC.