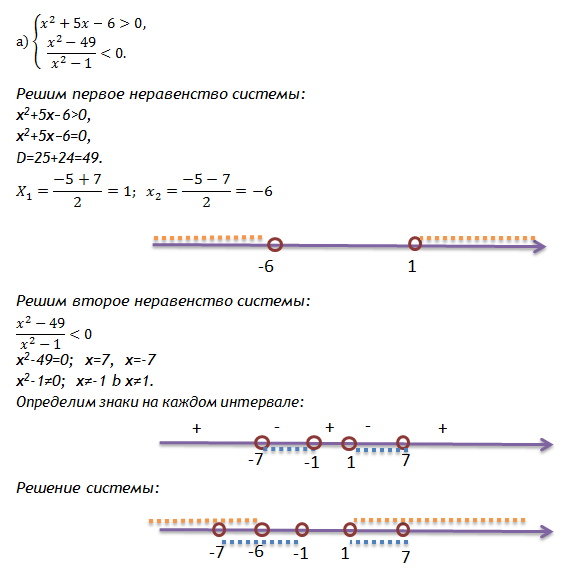
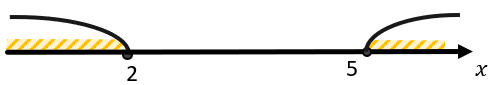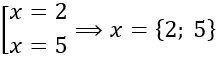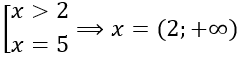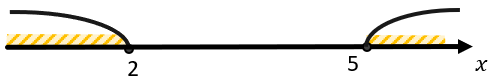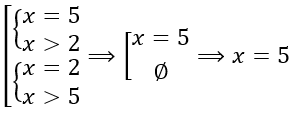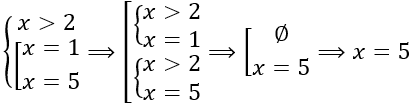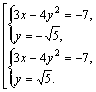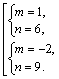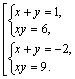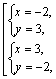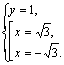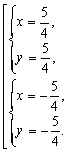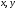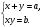Понятие совокупности неравенств с одной переменной и его решения
Несколько неравенств с одной переменной образуют совокупность, если нужно найти такое множество значений переменной, которое будет решением хотя бы одного из неравенств.
Решением совокупности неравенств с одной переменной является такое множество значений этой переменной, которое превращает хотя бы одно из неравенств в верное числовое неравенство.
Следствие: общим решением совокупности неравенств с одной переменной является объединение частных решений каждого из неравенств системы.
Например: $left[ begin{array}{cc} x+7 ge 2 \ x-4 lt 1 end{array} right. iff left[ begin{array}{cc} x ge -5 \ x lt 5 end{array} right. iff x in Bbb R$ — любое действительное число
Об объединении числовых промежутков подробней см. §17 данного справочника
Алгоритм решения совокупности неравенств с одной переменной
Шаг 1. Найти множество решений для каждого из неравенств системы. Если какое-либо частное решение является пустым множеством, отбросить его, но продолжить решение.
Шаг 2. Начертить друг под другом числовые прямые, число которых равно числу полученных непустых частных решений. Начала отсчёта числовых прямых должны находиться на общем перпендикуляре, единичный отрезок должен совпадать.
Шаг 3. На числовых прямых изобразить полученные частные решения, на отдельной прямой найти их объединение – это и будет общим решением совокупности.
Шаг 4. Работа завершена.
Например: $left[ begin{array}{cc} x-1 lt 0 \ x+5 ge 8 end{array} right. iff left[ begin{array}{cc} x lt 1 \ x ge 3 end{array} right. iff x lt 1 cup x ge 3 или x in (-infty;1) cup [3;+infty) $
Сравнение систем и совокупностей неравенств
Скобка
Фигурная
${left{ begin{array}{c} x+5 gt 3 \ x-7 lt 5 end{array} right.}$
Квадратная
$left[ begin{array}{cc} x+5 gt 3 \ x-7 lt 5 end{array} right.$
Пересечение
частных решений
$x gt -2 cap x lt 12 iff$
$ -2 lt x lt 12$
Объединение частных решений
$x gt -2 cap x lt 12 iff x in Bbb R$
Логическая операция
«ИЛИ»
Логическое сложение
Наличие одного частного решения $x in varnothing$
Вся система не имеет решений
$x in varnothing$
(аналогия с умножением на 0)
Вся совокупность может иметь
другие решения
(аналогия с прибавлением 0)
Неравенства могут образовывать сложные конструкции условий из вложенных систем и совокупностей. Раскрытие скобок при упрощении таких конструкций подчиняется законам логики и правилам операций над множествами (см. §10 данного справочника).
Примеры
Пример 1. Решите совокупности неравенств:
$ а) left[ begin{array}{cc} 5(x-1) ge 4(x+2) \ x lt 0 end{array} right. iff left[ begin{array}{cc} 5x-4x ge 8-5 \ x lt 0 end{array} right. iff left[ begin{array}{cc} x ge 3 \ x lt 0 end{array} right. iff x lt 0 cup x ge 3 $
$x in (-infty;0) cup [3;+infty) $
$ б) left[ begin{array}{cc} 2(x-5) gt x-11 \ x gt -3 end{array} right. iff left[ begin{array}{cc} 2x-x gt -11+10 \ x gt -3 end{array} right. iff left[ begin{array}{cc} x gt -1 \ x gt -3 end{array} right. iff x gt -3 $
$x in (-3;+infty) $
Пример 2. Решите неравенство:
$ а) (x+3)(x-5) lt 0 $
Произведение слева будет отрицательным, если сомножители будут иметь разные знаки. Получаем совокупность двух систем неравенств:
$ left[ begin{array}{cc} {left{ begin{array}{c} x+3 gt 0 \ x-5 lt 0 end{array} right.} \ {left{ begin{array}{c} x+3 lt 0 \ x-5 gt 0end{array} right.} end{array} right. iff left[ begin{array}{cc} {left{ begin{array}{c} x gt -3 \ x lt 5 end{array} right.} \ {left{ begin{array}{c} x lt -3 \ x gt 5 end{array} right.} end{array} right. iff left[ begin{array}{cc} -3 lt x lt 5 \ x in varnothing end{array} right. iff -3 lt x lt 5 $
$ x in (-3;5) $
$ б) (2x+3)(3x-2) ge 0 $
Произведение слева будет положительным (или равным 0), если сомножители будут иметь одинаковые знаки (или равными 0).
Получаем совокупность двух систем неравенств:
$ left[ begin{array}{cc} {left{ begin{array}{c} 2x+3 ge 0 \ 3x-2 ge 0 end{array} right.} \ {left{ begin{array}{c} 2x+3 le 0 \ 3x-2 le 0 end{array} right.} end{array} right. iff left[ begin{array}{cc} {left{ begin{array}{c} x ge -1,5 \ x ge frac{2}{3} end{array} right.} \ {left{ begin{array}{c} x le -1,5 \ x le frac{2}{3} end{array} right.} end{array} right. iff left[ begin{array}{cc} x ge frac{2}{3} \ x le -1,5 end{array} right. iff xle-1,5 cup xge frac{2}{3} $
$ x in (-infty;-1,5] cup [frac{2}{3};+infty) $
Пример 3*. Решите неравенство: $(x^2+3x-4)(x^2+3x) lt 0$
Замена переменных: $ {left{ begin{array}{c} x^2+3x = t \ (t-4)t lt 0 end{array} right.}$
Для нижнего неравенства получаем совокупность:
$ left[ begin{array}{cc} {left{ begin{array}{c} t-4 gt 0 \ t lt 0 end{array} right.} \ {left{ begin{array}{c} t-4 lt 0 \ t gt 0end{array} right.} end{array} right. iff left[ begin{array}{cc} {left{ begin{array}{c} t gt 4 \ t lt 0 end{array} right.} \ {left{ begin{array}{c} t lt 4 \ t gt 0 end{array} right.} end{array} right. iff left[ begin{array}{cc} t in varnothing \ 0 lt t lt 4 end{array} right. iff 0 lt t lt 4 $
Возвращаемся к исходной переменной
$$ 0 lt x^2+3x lt 4 iff {left{ begin{array}{c} x^2+3x gt 0 \ x^2+3x lt 4 end{array} right.} iff {left{ begin{array}{c} x^2+3x gt 0 \ x^2+3x-4 lt 0 end{array} right.} iff {left{ begin{array}{c} x(x+3) gt 0 \ (x+4)(x-1) lt 0 end{array} right.} iff $$
$$ iff {left{ begin{array}{c} left[ begin{array}{cc} {left{ begin{array}{c} x gt 0 \ x+3 gt 0 end{array} right.} \ {left{ begin{array}{c} x lt 0 \ x+3 lt 0 end{array} right.} end{array} right. \ left[ begin{array}{cc} {left{ begin{array}{c} x+4 gt 0 \ x-1 lt 0 end{array} right.} \ {left{ begin{array}{c} x+4 lt 0\ x-1 gt 0 end{array} right.} end{array} right. end{array} right.} iff {left{ begin{array}{c} left[ begin{array}{cc} {left{ begin{array}{c} x gt 0 \ x gt -3end{array} right.} \ {left{ begin{array}{c} x lt 0 \ x lt -3 end{array} right.} end{array} right. \ left[ begin{array}{cc} {left{ begin{array}{c} x gt -4 \ x lt 1 end{array} right.} \ {left{ begin{array}{c} x lt -4 \ x gt 1 end{array} right.} end{array} right. end{array} right.} iff {left{ begin{array}{c} left[ begin{array}{cc} x gt 0 \ x lt -3 end{array} right. \ left[ begin{array}{cc} -4 lt x lt 1 \ x in varnothing end{array} right. end{array} right.} iff {left{ begin{array}{c} x lt -3 cup x gt 0 \ -4 lt x lt 1 end{array} right.} iff $$
$$ iff -4 lt x lt -3 cup 0 lt x lt 1 $$
$x in (-4;-3) cup (0;1)$
В 9 классе для решения подобных неравенств будет предложен очень эффективный метод интервалов, который позволяет значительно упростить ход решения.
Системы и совокупности уравнений с одной переменной
СИСТЕМА:
Ключевым моментом в решении систем уравнений является понимание самой сути системы. Система означает, что необходимо учитывать решения нескольких уравнений или нескольких неравенств при записи решения. То есть нужно решить и первое, и второе уравнение/неравенство, ответом самой системы будет пересечение этих ответов.
Рассмотрим несколько простейших систем.
(left{ begin{matrix} x = 2 \ x = 5 \ end{matrix} right. Longrightarrow varnothing)
Решением системы являются все значения переменной, при которых выполняются все перечисленные условия. Может ли x одновременно равняться и 2, и 5? Нет, поэтому у этой системы решений нет.
Часто системы усложняются неравенствами.
(left{ begin{matrix} x > 2 \ x = 5 \ end{matrix} right. Longrightarrow x = 5)
В этой системе требуется, чтобы x был одновременно и равен 5, и был больше 2. При каких значениях это возможно? Только при (x = 5).
Рассмотрим ещё одну систему:
(left{ begin{matrix} x < 2 \ x > 5 \ end{matrix} right. Longrightarrow varnothing)
Мы видим 2 отрезка, у которых нет пересечения, поэтому корней данная система не имеет.
СОВОКУПНОСТЬ:
Также иногда вам придётся работать с совокупностью. Совокупность предполагает вариативность: может выполняться ИЛИ то, ИЛИ другое условие.
Например:
В ответ пойдут обе точки: и 2, и 5. Обратите внимание, что если у нас в ответе конечное количество точек, то их принято писать в фигурных скобочках.
Там подходят или 5, или те x, которые больше 2. Но 5 больше 2, значит, нам просто подходит промежуток от 2 до бесконечности.
Здесь мы будем рассматривать объединение: если x является корнем хотя бы одного уравнения, неравенства из совокупности, значит, он уже является решением.
КОМБИНАЦИИ СИСТЕМ И СОВОКУПНОСТЕЙ:
Но и это ещё не всё. Иногда совокупность включает в себя систему или система включает себя совокупность. Давайте посмотрим.
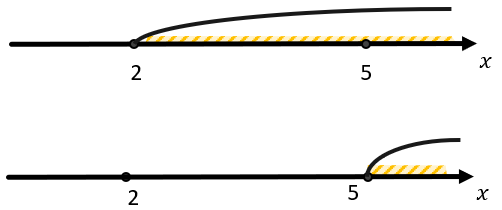
Такая ситуация называется «совокупность двух систем». То есть в ответ пойдут все x, которые удовлетворяют первой системе, и все x, которые удовлетворяют второй системе. Поэтому для того, чтобы её решить, нужно сначала решить внутренние системы, а затем в ответ написать все полученные в них корни.
Следующий пример немного другой:
Итак, у нас есть система. Это означает, что должно выполняться 2 условия:
1. x должен быть больше 2.
2. x должен быть равен либо 1, либо 5.
В таких случаях необходимо рассмотреть каждый корень из второго условия на соответствие первому, то есть перейти к совокупности двух систем.
Пусть даны два уравнения с двумя неизвестными и
где
– некоторые выражения с переменными Х и У. Если ставится задача найти все общие решения данных уравнений, то говорят, что задана Система уравнений:
(3.15)
Решить систему (3.15) – значит найти все пары чисел которые являются решением каждого уравнения, или доказать, что таких пар чисел не существует.
Аналогично определяется понятие системы с тремя и более неизвестными.
Системы, все уравнения которых однородные, называются Однородными системами уравнений.
Система называется Совместной, если она имеет хотя бы одно решение и Несовместной, если таких решений не существует.
Две системы уравнений Эквивалентны (Равносильны), если они имеют одни и те же решения или обе не имеют решений.
Над уравнениями системы можно выполнять следующие действия, преобразующие данную систему в эквивалентную ей:
1) менять порядок следования уравнений;
2) умножать на число любое уравнение;
3) умножать на число одно уравнение системы и прибавлять его к другому уравнению.
Несколько уравнений образуют Совокупность уравнений
Если ставится задача найти все те решения, которые удовлетворяют хотя бы одному уравнению совокупности и входят в область определения остальных уравнений.
Система двух линейных уравнений с двумя неизвестными имеет вид:
(3.16)
Где
Геометрически каждому уравнению системы (3.16) соответствует прямая линия на плоскости:
и
Справедливы утверждения:
1) если то система (3.16) имеет единственное решение (геометрически – прямые
пересекаются в определенной точке);
2) если то система (3.16) не имеет решений (прямые
параллельны);
3) если то система (3.16) имеет бесконечно много решений (прямые
и
– совпадают).
Основными методами решения систем уравнений (3.15) являются:
1) метод подстановки;
2) метод исключения неизвестной;
3) метод сложения;
4) метод умножения (деления) уравнений;
5) метод замены переменных;
6) графический метод.
Пример 1. Решить систему
Решение. Решим методом сложения. Для этого первое уравнение системы умножим на и прибавим ко второму:
Откуда следует
Получаем
т. е.
Следовательно,
Заданная система сводится к решению совокупности систем:
Ее решением являются пары чисел:
Пример 2. Решить систему
Решение. ОДЗ:
Заменим в первом уравнении системы тогда
Получим дробно-рациональное уравнение:
Решаем его
Возвращаемся к переменным Х, У:
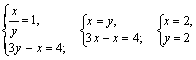
Получили ответ
Пример 3. Решить систему
Решение. Данная система относится к Симметрическим системам (неизвестные входят одинаково). Решение таких систем производят стандартной заменой переменных
(3.17)
Далее используем метод сложения:
т. е.
Получаем корни этого квадратного уравнения:
С учетом системы (3.17) имеем:
Возвращаясь к переменным Х, У, получаем:
Решим записанные системы отдельно:
1) (3.18)
Возвращаясь к системе (3.18), получаем:
Т. е. имеем два решения и
2) (3.19)
Поскольку для последнего квадратного уравнения система (3.19) не имеет решения.
Получили ответ
Пример 4. Решить систему графически:
1) (3.20)
2)
Решение. 1) Исходя из геометрического смысла, – уравнение окружности с центром
и радиусом
– прямая, параллельная оси Ох и проходящая через точку
Построим эти линии (рис. 3.2).
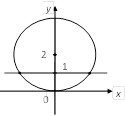 |
Рис. 3.2
Графики имеют две точки пересечения, т. е. система имеет два решения, которые найдем из системы (3.20):
Получили ответ
2) Уравнение может быть записано в виде
и является уравнением гиперболы.
Уравнение может быть записано в виде
– это биссектриса II и IV координатных углов.
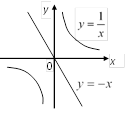
Рис. 3.3
Графики не имеют точек пересечения и, следовательно, система решений не имеет.
Пример 5. Решить систему
Решение. Система содержит однородное уравнение.
Так как получим:
Из второго уравнения найдем Х:
Получаем совокупность двух систем:
Приходим к ответу и
| < Предыдущая | Следующая > |
|---|
13. Системы неравенств
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Если ставится задача найти множество общих решений двух или более неравенств, то говорят, что надо решить систему неравенств.
Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда системы неравенств записывают в виде двойного неравенства:
-5<x<12 или
Решением системы неравенств называется число, которое при его подстановке в систему обращает каждое неравенство в верное числовое неравенство.
Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет.
Чтобы решить систему неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это пересечение и является множеством решений системы неравенств.
Пример:
Решить систему неравенств:
Решим каждое неравенство в отдельности
1) 5x-x2≥0,
5x-x2=0,
x(5-x)=0,
x=0 или 5-x=0,
-x=-5,
x=5.
Находим решение с помощью метода интервалов:
2) 6-2x<-2,
-2x<-2-6,
-2x<-8,
x>-8:(-2),
x>4.
Объединим оба решения:
Ответ: (4; 5].
Говорят, что несколько неравенств с одной переменной образуют совокупность, если необходимо найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств. Совокупность неравенств обозначается квадратной скобкой.
Решением совокупности неравенств называют такие значения переменной, которые являются верными хотя бы для одного из этих неравенств.
Чтобы решить совокупность неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти объединение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это объединение и является решением совокупности неравенств.
Пример:
Решить совокупность неравенств:
Решим каждое неравенство в отдельности
1) 5х+6≤1,
5х≤ -5,
х≤ -1.
2) 2х+1≥3,
2х≥2,
х≥1.
Объединим оба решения:
Ответ: (-∞; -1]U[1;+∞).
УПРАЖНЕНИЯ
1. Решите систему неравенств:
Решение:
а)
Ответ: (5; 7]
2. Решите систему неравенств:
Решение:
Ответ: (1; 10].
3. Найдите целые решения системы неравенств:
Решение:
а)
Ответом являются все целые числа, которые принадлежат промежутку (-15; 5).
Ответ: -14; -13; -12; -11; -10; -9; -8; -7; -6.
4. Решите систему неравенств:
Решение:
Ответ: (-1; 3).
5. Решите систему неравенств:
Решение:
Ответ: (-1;2).
6. Решите систему неравенств:
Решение:
Ответ: нет решений.
7. Решите систему неравенств:
Решение:
Ответ: (0; +∞).
8. Решите неравенство:
а) -2<3x+5≤10; б) 2<4x+6≤12.
Решение:
а) -2 < 3x+5 ≤ 10;
-2-5
< 3x ≤ 10-5;
-7
< 3x ≤ 5;
-7:3
< x ≤ 5:3;
-7/3
< x ≤ 5/3.
Ответ: (-2 1/3; 1 2/3].
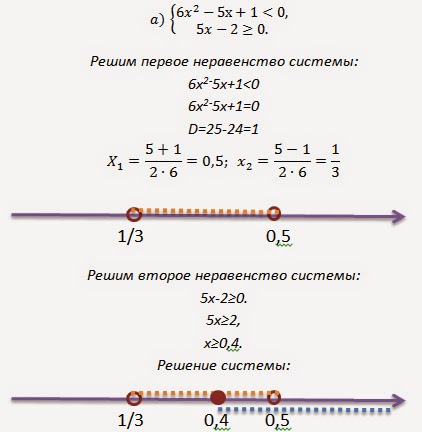
9. Решите систему неравенств:
Решение:
Ответ: [0,4; 0,5).
10. Решите систему неравенств (№ 3.4.52 [7]):
Решение:
Ответ: (-1; 2).
11. Решите систему неравенств:
Решение:
Ответ: [-9; 3)U(3; 9].
12. Решите систему неравенств:
Решение:
Ответ: (-7; -6)U(1;7).
13. Решите систему неравенств:
Решение:
Ответ: (2; 4).
14. Решите систему неравенств:
Решение:
Ответ: (-7; -2)U(0; 2).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решите систему неравенств:
2. Решите систему неравенств:
3. Решите систему неравенств:
4. Решите систему неравенств:
5. Решите систему неравенств:
6. Решите систему неравенств:
7. Решите систему неравенств:
8. Решите систему неравенств:
9. Решите систему неравенств:
10. Решите систему неравенств:
Проверь себя
Системой
уравнений
называется несколько совместно
рассматриваемых уравнений, для которых
требуется найти значения всех содержащихся
в них неизвестных, удовлетворяющие
одновременно всем этим уравнениям.
Решением
системы уравнений
называется упорядоченный набор значений
неизвестных, удовлетворяющий одновременно
всем уравнениям системы.
Совместной
называется
система уравнений, имеющая решения.
Система уравнений, не имеющая решений,
называется несовместной.
Основные
методы решения систем двух уравнений
с двумя неизвестными
-
Метод
подстановки.
В каком-либо уравнении выражаем одну
неизвестную через другую и подставляем
в другое уравнение с целью исключения
одной неизвестной. -
Метод
сложения. В
результате умножения одного из уравнений
системы на число и прибавления ко
второму уравнению, получается
равносильная система. Метод используют
с целью, чтобы в результате сложения
одна из неизвестных исчезла или было
получено более простое уравнение. -
Метод
умножения (деления).
Если свободные члены не равны нулю,
то одно из уравнений системы можно
заменить уравнением, которое получено
в результате почленного умножения
(деления) заданных уравнений системы. -
Метод
замены переменных.
Если уравнения системы содержат
одинаковые выражения, их заменяют
новыми переменными. Замену производят
в двух уравнениях сразу или решают
вначале отдельно заменой одно уравнение
системы (вводя одну неизвестную), а
затем возвращаются к решению системы.
Заменой
переменной решают, в частности,
симметрические
системы
– это такие системы, которые не изменяются,
если неизвестные
взаимно заменить одна другой (т.е. они
входят в систему одинаково). Для решения
таких систем делают стандартную замену
-
Графический
метод. Строят
графики функций (или кривые), которые
соответствуют уравнениям системы.
Находят координаты точек пересечения
этих графиков. Данным метод решения
не всегда дает точное решение.
Эти
приемы обобщаются на решение систем с
большим количеством уравнений и
неизвестных.
Системы и совокупности уравнений
Система
уравнений.
Задана система двух уравнений с одной
переменной, если требуется найти все
значения переменной. при которых оба
уравнения системы обращаются в верные
равенства.
Решение
системы уравнений. Решением системы
уравнений называют значение переменной,
образующие оба уравнения системы в
верные числовые равенства.
Совокупность
уравнений.
Задана совокупность двух уравнений с
одной переменной, если требуется найти
все такие значения переменной, при
каждом из которых хотя бы одно из
уравнений совокупности обращаются в
верное числовое равенство.
Решение
совокупности уравнений. Решением
совокупности уравнений называют значение
переменной, образующее хотя бы одно из
уравнений совокупности в верное числовое
равенство.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #