Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени ( 0 , 5 ) 5 .
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Условие: возведите — 2 в степень 4 .
Решение
Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 .
Возьмем пример посложнее.
Вычислите значение 3 2 7 2
Решение
Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Выполните возведение в квадрат числа π .
Решение
Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи 
От основания степени это не зависит.
Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .
5 0 = 1 , ( — 2 , 56 ) 0 = 1 2 3 0 = 1
0 0 — не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Возведите 2 в степень — 3 .
Решение
Используя определение выше, запишем: 2 — 3 = 1 2 3
Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 .
Тогда ответ таков: 2 — 3 = 1 2 3 = 1 8
Возведите 1 , 43 в степень — 2 .
Решение
Переформулируем: 1 , 43 — 2 = 1 ( 1 , 43 ) 2
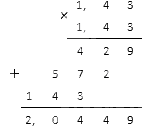
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло ( 1 , 43 ) — 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: ( 1 , 43 ) — 2 = 10000 20449
Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a — 1 = 1 a 1 = 1 a .
Пример: 3 − 1 = 1 / 3
9 13 — 1 = 13 9 6 4 — 1 = 1 6 4 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.
У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m .
Проиллюстрируем на примере.
Вычислите 8 — 2 3 .
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8 — 2 3 = 8 — 2 3
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 — 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Способ 2. Преобразуем основное равенство: 8 — 2 3 = 8 — 2 3 = 8 3 — 2
После этого извлечем корень 8 3 — 2 = 2 3 3 — 2 = 2 — 2 и результат возведем в квадрат: 2 — 2 = 1 2 2 = 1 4
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Возведите 44 , 89 в степень 2 , 5 .
Решение
Преобразуем значение показателя в обыкновенную дробь — 44 , 89 2 , 5 = 49 , 89 5 2 .
А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107
Ответ: 13 501 , 25107 .
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную — значения не имеет: 0 — 4 3 .
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Вычислите приближенное значение 21 , 174367 .
Решение
Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .
Ещё Ричард Фейнман в книге «Вы конечно шутите, мистер Фейнман!» поведал несколько приёмов устного счёта. Хотя это очень простые трюки, они не всегда входят в школьную программу.
Например, чтобы быстро возвести в квадрат число X около 50 (50 2 = 2500), нужно вычитать/прибавлять по сотне на каждую единицы разницы между 50 и X, а потом добавить разницу в квадрате. Описание звучит гораздо сложнее, чем реальное вычисление.
52 2 = 2500 + 200 + 4
47 2 = 2500 – 300 + 9
58 2 = 2500 + 800 + 64
Молодого Фейнмана научил этому трюку коллега-физик Ханс Бете, тоже работавший в то время в Лос-Аламосе над Манхэттенским проектом.
Ханс показал ещё несколько приёмов, которые использовал для быстрых вычислений. Например, для вычисления кубических корней и возведения в степень удобно помнить таблицу логарифмов. Это знание очень упрощает сложные арифметические операции. Например, вычислить в уме примерное значение кубического корня из 2,5. Фактически, при таких вычислениях в голове у вас работает своеобразная логарифмическая линейка, в которой сложение и деление чисел заменяется сложением и вычитанием их логарифмов. Удобнейшая вещь.

Логарифмическая линейка
До появления компьютеров и калькуляторов логарифмическую линейку использовали повсеместно. Это своеобразный аналоговый «компьютер», позволяющий выполнить несколько математических операций, в том числе умножение и деление чисел, возведение в квадрат и куб, вычисление квадратных и кубических корней, вычисление логарифмов, потенцирование, вычисление тригонометрических и гиперболических функций и некоторые другие операции. Если разбить вычисление на три действия, то с помощью логарифмической линейки можно возводить числа в любую действительную степень и извлекать корень любой действительной степени. Точность расчётов — около 3 значащих цифр.
Чтобы быстро проводить в уме сложные расчёты даже без логарифмической линейки, неплохо запомнить квадраты всех чисел, хотя бы до 25, просто потому что они часто используются в расчётах. И таблицу степеней — самых распространённых. Проще запомнить, чем вычислять каждый раз заново, что 5 4 = 625, 3 5 = 243, 2 20 = 1 048 576, а √3 ≈ 1,732.
Ричард Фейнман совершенствовал свои навыки и постепенно замечал всё новые интересные закономерности и связи между числами. Он приводит такой пример: «Если кто-то начинал делить 1 на 1,73, можно было незамедлительно
ответить, что это будет 0,577, потому что 1,73 — это число, близкое к квадратному корню из трёх. Таким образом, 1/1,73 — это около одной трети квадратного корня из 3».
Настолько продвинутый устный счёт мог бы удивить коллег в те времена, когда не было компьютеров и калькуляторов. В те времена абсолютно все учёные умели хорошо считать в уме, поэтому для достижения мастерства требовалось достаточно глубоко погрузиться в мир цифр.
В наше время люди достают калькулятор, чтобы просто поделить 76 на 3. Удивить окружающих стало гораздо проще. Во времена Фейнмана вместо калькулятора были деревянные счёты, на которых тоже можно было производить сложные операции, в том числе брать кубические корни. Великий физик уже тогда заметил, что использование таких инструментов, людям вообще не нужно запоминать множество арифметический комбинаций, а достаточно просто научиться правильно катать шарики. То есть люди с «расширителями» мозга не знают чисел. Они хуже справляются с задачами в «автономном» режиме.
Вот пять очень простых советов устного счёта, которые рекомендует Яков Перельман в методичке «Быстрый счёт» 1941 года издательства.
1. Если одно из умножаемых чисел разлагается на множители, удобно бывает последовательно умножать на них.
225 × 6 = 225 × 2 × 3 = 450 × 3
147 × 8 = 147 × 2 × 2 × 2, то есть трижды удвоить результат
2. При умножении на 4 достаточно дважды удвоить результат. Аналогично, при делении на 4 и 8, число делится пополам дважды или трижды.
3. При умножении на 5 или 25 число можно разделить на 2 или 4, а затем приписать к результату один или два нуля.
74 × 5 = 37 × 10
72 × 25 = 18 × 100
Здесь лучше сразу оценивать, как проще. Например, 31 × 25 удобнее умножать как 25 × 31 стандартным способом, то есть как 750+25, а не как 31 × 25, то есть 7,75 × 100.
При умножении на число, близкое к круглому (98, 103), удобно сразу умножить на круглое число (100), а затем вычесть/прибавить произведение разницы.
37 × 98 = 3700 – 74
37 × 104 = 3700 + 148
4. Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 85), умножают число десятков (8) на него же плюс единица (9), и приписывают 25.
8 × 9 = 72, приписываем 25, так что 85 2 = 7225
Почему действует это правило, видно из формулы:
(10Х + 5) 2 = 100Х 2 + 100Х + 25 = 100Х (X+1) + 25
Приём применяется и к десятичным дробям, которые оканчиваются на 5:
8,5 2 = 72,25
14,5 2 = 210,25
0,35 2 = 0,1225
5. При возведении в квадрат не забываем об удобной формуле
(a + b) 2 = a 2 + b 2 + 2ab
44 2 = 1600 + 16 + 320
Конечно же, все способы можно сочетать между собой, создавая более удобные и эффективные приёмы для конкретных ситуаций.
Алгоритмы быстрого возведения в степень (дихотомический алгоритм возведения в степень, бинарный алгоритм возведения в степень) — алгоритмы, предназначенные для возведения числа x <displaystyle x> 















Кроме того, некоторые алгоритмы для дальнейшей оптимизации используют тот факт, что операция возведения в квадрат быстрее операции умножения за счёт того, что при возведении в квадрат цифры в сомножителе повторяются [2] .
Бинарный алгоритм возведения в степень был впервые предложен в XV веке персидским математиком Аль-Каши [3] .
Данные алгоритмы не всегда оптимальны. Например, при использовании схемы «слева направо» быстрое возведение в степень n = 15 потребует выполнения трёх операций умножения и трёх операций возведения в квадрат, хотя возведение в 15-ю степень можно выполнить и за 3 умножения и 2 возведения в квадрат [4] .
Содержание
Описание [ править | править код ]
Основным алгоритмом быстрого возведения в степень является схема «слева направо». Она получила своё название вследствие того, что биты показателя степени просматриваются слева направо, то есть от старшего к младшему [5] .
n = ( m k m k − 1 . . . m 1 m 0 ¯ ) 2 <displaystyle n=(<overline m_. m_<1>m_<0>>>)_<2>> 
где m k = 1 , m i ∈ < 0 , 1 ><displaystyle m_=1,m_in <0,1>> 
x n = x ( ( … ( ( m k ⋅ 2 + m k − 1 ) ⋅ 2 + m k − 2 ) ⋅ 2 + … ) ⋅ 2 + m 1 ) ⋅ 2 + m 0 = ( ( … ( ( ( x m k ) 2 ⋅ x m k − 1 ) 2 … ) 2 ⋅ x m 1 ) 2 ⋅ x m 0 <displaystyle x^=x^<((dots ((m_cdot 2+m_)cdot 2+m_)cdot 2+dots )cdot 2+m_<1>)cdot 2+m_<0>>=((dots (((x^>)^<2>cdot x^>)^<2>dots )^<2>cdot x^<1>>)^<2>cdot x^<0>>> 
Последовательность действий при использовании данной схемы можно описать так:
- Представить показатель степени n в двоичном виде
- Если m i <displaystyle m_>
= 1, то текущий результат возводится в квадрат и затем умножается на x. Если m i <displaystyle m_>
= 0, то текущий результат просто возводится в квадрат [6] . Индекс i изменяется от k-1 до 0 [7] .
Таким образом, алгоритм быстрого возведения в степень сводится к мультипликативному аналогу схемы Горнера [6] :
Обобщения [ править | править код ]
Пусть пара (S, *) — полугруппа, тогда мы можем назвать операцию * умножением и определить операцию возведения в натуральную степень:
1end>
ight.>»> a n = < a n = 1 a ∗ ( a n − 1 ) n >1 <displaystyle a^=left<<egina&n=1a*left(a^
ight)&n>1end>
ight.> 
ight.»/>
Тогда для вычисления значений a n в любой полугруппе (в абелевой группе в частности) можно использовать алгоритмы быстрого возведения в степень [8] .
Примеры решения задач [ править | править код ]
Применяя алгоритм, вычислим 21 13 :
13 10 = 1101 2 <displaystyle 13_<10>=1101_<2>> 

Схема «справа налево» [ править | править код ]
В данной схеме, в отличие от схемы «слева направо», биты показателя степени просматриваются от младшего к старшему [5] .
Последовательность действий при реализации данного алгоритма.
- Представить показатель степени n в двоичном виде.
- Положить вспомогательную переменную z равной числу x.
- Если m i = 1 <displaystyle m_=1>
, то текущий результат умножается на z, а само число z возводится в квадрат. Если m i <displaystyle m_>
= 0, то требуется только возвести z в квадрат [6] . При этом индекс i, в отличие от схемы слева направо, изменяется от 0 до k-1 включительно [7] .
Данная схема содержит столько же умножений и возведений в квадрат, сколько и схема «слева направо». Однако несмотря на это, схема «слева направо» выгоднее схемы «справа налево», особенно в случае, если показатель степени содержит много единиц. Дело в том, что в схеме слева направо в операции result = result · x содержится постоянный множитель x. А для небольших x (что нередко бывает в тестах простоты) умножение будет быстрым. К примеру, для x = 2 мы можем операцию умножения заменить операцией сложения [7] .
Математическое обоснование работы данного алгоритма можно представить следующей формулой:
d = a n = <displaystyle d=a^=> 




Пример. Посчитаем с помощью схемы возведения в степень «справа налево» значение 21 13 .
| i | 1 | 2 | 3 | |
|---|---|---|---|---|
a 2 i <displaystyle a^<2^>> |
21 | 441 | 194 481 | 37 822 859 361 |
m 1 <displaystyle m_<1>> |
1 | 1 | 1 |
- 21 · 194 481 = 4084 101
- 4084 101 · 37 822 859 361 = 154 472 377 739 119 461
Вычислительная сложность [ править | править код ]
И для схемы «слева направо», и для схемы «справа налево» количество операций возведения в квадрат одинаково и равно k, где k — длина показателя степени n в битах, k ∼ ln n <displaystyle ksim ln > 

Например, для возведения числа в сотую степень этим алгоритмом потребуется всего лишь 8 операций умножения и возведения в квадрат [5] .
Для сравнения, при стандартном способе возведения в степень требуется n − 1 <displaystyle n-1> 

Оптимизация алгоритма [ править | править код ]
Как правило, операция возведения в квадрат выполняется быстрее операции умножения. Метод окон позволяет сократить количество операций умножения и, следовательно, сделать алгоритм возведения в степень более оптимальным [8] .
Окно фактически представляет собой основание системы счисления [7] . Пусть w — ширина окна, то есть за один раз учитывается w знаков показателя.
Рассмотрим метод окна.
- Для i = 0 , 2 w − 1 ¯ <displaystyle i=<overline <0,2^-1>>>
заранее вычисляется x i
- Показатель степени представляется в следующем виде: n = ∑ i = 0 k / w n i ⋅ 2 i ⋅ w <displaystyle n=sum _^cdot 2^>>
, где n i ∈ ( 0 , 1 , . . . , 2 w − 1 ) <displaystyle n_in <(0,1. 2^-1)>>
- Пусть y — переменная, в которой будет вычислен конечный результат. Положим y = x n k / w <displaystyle y=x^>>
.
- Для всех i = k/w — 1, k/w — 2, …, 0 выполнить следующие действия:
- y = y 2 w <displaystyle y=y^<2^>>
- y = y ⋅ x n i <displaystyle y=ycdot x^>>
[8] .
В данном алгоритме требуется k возведений в квадрат, но число умножений в среднем сокращается до k/w [8] .
Ещё более эффективным является метод скользящего окна. Он заключается в том, что ширина окна во время выполнения процесса может изменяться:
- Показатель степени представляется в виде n = ∑ i = 0 l n i ⋅ 2 e i <displaystyle n=sum _^cdot 2^>>>
, где n i ∈ ( 1 , 3 , 5 , . . . , 2 w − 1 ) <displaystyle n_in <(1,3,5. 2^-1)>>
, а ei+1 — ei ≥ w.
- Для i = ( 1 , 3 , 5 , . . . , 2 w − 1 ) <displaystyle i=(1,3,5. 2^-1)>
вычисляется x i . Далее будем обозначать x i как xi.
- Пусть y — переменная, в которой будет вычислен конечный результат. Положим y = x n l <displaystyle y=x^>>
.
- Для всех i = l — 1, l — 2, …, 0 выполнить следующие действия:
- Для всех j от 0 до ei+1 — ei — 1 y возвести в квадрат
- j = m i <displaystyle j=m_>
- y = y ⋅ x j <displaystyle y=ycdot x_>
Количество операций возведения в степень в данном алгоритме такое же, как и в методе окна, а вот количество операций умножений сократилось до l, то есть до k w + 1 <displaystyle <frac >> 
Для примера возведём методом скользящего окна число x в степень 215. Ширина окна w = 3.
- 215 = 2 7 + 5 · 2 4 + 7
- y = 1
- y = y · x = x
- y 3 раза возводится в квадрат, так как на данном шаге e2 — e1 −1 = 7 — 4 — 1 = 2, а отсчёт ведётся с нуля, то есть y = y 8 = x 8
- y = y · x 5 = x 13
- y 4 раза возводится в квадрат, так как на данном шаге e1 — e −1 = 4 — 0 — 1 = 3, то есть y = y 16 = x 208
- y = y · x 7 = x 215
Применение [ править | править код ]
Алгоритм быстрого возведения в степень получил широкое распространение в криптосистемах с открытым ключом. В частности, алгоритм применяется в протоколе RSA, схеме Эль-Гамаля и других криптографических алгоритмах [11] .
Таблица степеней
Скачать таблицу степеней
Определение. Возведение в степень — операция, происходящая из сокращения для множественного умножения числа на самого себя.
| an = | a · a · … · a |
 |
|
| n |
Калькулятор для вычисления степени числа
= 9
Таблица степеней чисел от 1 до 10
|
11 = 1 12 = 1 13 = 1 14 = 1 15 = 1 16 = 1 17 = 1 18 = 1 19 = 1 110 = 1 |
21 = 2 22 = 4 23 = 8 24 = 16 25 = 32 26 = 64 27 = 128 28 = 256 29 = 512 210 = 1024 |
31 = 3 32 = 9 33 = 27 34 = 81 35 = 243 36 = 729 37 = 2187 38 = 6561 39 = 19683 310 = 59049 |
41 = 4 42 = 16 43 = 64 44 = 256 45 = 1024 46 = 4096 47 = 16384 48 = 65536 49 = 262144 410 = 1048576 |
51 = 5 52 = 25 53 = 125 54 = 625 55 = 3125 56 = 15625 57 = 78125 58 = 390625 59 = 1953125 510 = 9765625 |
|
61 = 6 62 = 36 63 = 216 64 = 1296 65 = 7776 66 = 46656 67 = 279936 68 = 1679616 69 = 10077696 610 = 60466176 |
71 = 7 72 = 49 73 = 343 74 = 2401 75 = 16807 76 = 117649 77 = 823543 78 = 5764801 79 = 40353607 710 = 282475249 |
81 = 8 82 = 64 83 = 512 84 = 4096 85 = 32768 86 = 262144 87 = 2097152 88 = 16777216 89 = 134217728 810 = 1073741824 |
91 = 9 92 = 81 93 = 729 94 = 6561 95 = 59049 96 = 531441 97 = 4782969 98 = 43046721 99 = 387420489 910 = 3486784401 |
101 = 10 102 = 100 103 = 1000 104 = 10000 105 = 100000 106 = 1000000 107 = 10000000 108 = 100000000 109 = 1000000000 1010 = 10000000000 |
Распечатать таблицу степеней
Таблица степеней
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3n | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4n | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5n | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6n | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7n | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8n | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9n | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10n | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Распечатать таблицу степеней
Как посчитать степень
- Главная
- /
- Математика
- /
- Арифметика
- /
- Как посчитать степень
Для того чтобы возвести любое число в любую степень воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Просто введите число и степень, в которую хотите его возвести, и получите ответ.
Теория
Возведение в степень – это математическая операция, при которой число умножается само на себя энное количество раз в зависимости от значения степени.
Формула
an=a⋅a⋅a…и так n-раз
Пример
К примеру, возведём число 2 в 3-ю степень:
23 = 2⋅2⋅2 = 4⋅2 = 8
Как посчитать отрицательную степень
Возведение в отрицательную (минусовую) степень происходит по следующей формуле:
Формула
a-n = 1/an
Пример
К примеру, возведём число 2 в −3-ю степень:
2-3 = 1/(2⋅2⋅2) = 1/(4⋅2) = 1/8 = 0,125
Как посчитать дробную степень
Возведение числа в дробную степень происходит по следующей формуле:
Формула
an/m = m√an
Пример
К примеру, возведём число 4 в степень 0.5:
40.5 = 4½ = 2√41 = 2
Теперь пример посложней: возведём число 2 в степень ¾:
2¾ = 4√23 ≈ 1.6817
См. также
Таблицы натуральных чисел в степенях
Высчитывать число в степени «вручную» можно только при небольших значениях (например: 23=2*2*2=8). Но когда дело касается больших цифр (например: 693), то найти значение конкретного числа путем его перемножения на себя указанное количество раз будет сложно. Для упрощения вычислений представлено множество различных таблиц степеней, которые уже представляют готовые ответы такого «перемножения». Количество версий таких структур практически не ограничено. Сегодня попробуем разобрать наиболее популярные и простые в использовании варианты.
Традиционная таблица степеней натуральных чисел: от 1 до 10
Проще всего находить значение многократного перемножения небольших натуральных чисел. Для поиска решения можно использовать следующую подсказку:
По методу вычисления эта таблица натуральных степеней схожа с таблицей умножения. Чтобы найти результат произведения числа нужное количество раз, достаточно найти соответствующую формулу в столбике.
Пример 1. Используем простую таблицу степеней по алгебре.
Задача. Найти 79.
Решение. Находим 79. Расположено значение во втором столбике нижней строки.
Ответ. 40353607.
Пример 2. Используем простую таблицу по алгебре.
Задача. Найти 17.
Решение. В данном случае найти значение выражения можем без использования вспомогательных инструментов. Достаточно вспомнить одно из свойств степеней: единица всегда остается единицей.
Ответ. 1.
Таблица степеней по алгебре: числа в квадрате
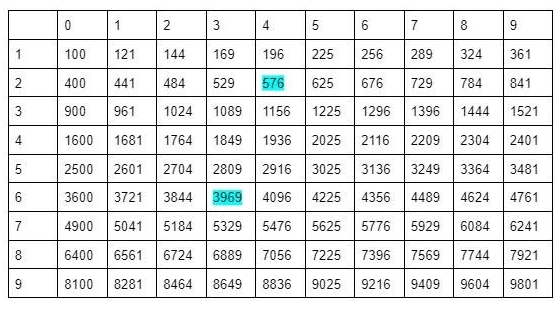
Расписать абсолютно каждое число и найти его значение во всех степенях — невозможно. В сложных примерах рекомендуется использовать онлайн калькуляторы. Мы же рассматриваем наиболее примитивные и распространенные случаи. В основном, в средней школе (вплоть до 11 класса) рассматриваются примеры с перемножением незначительное количество раз. Часто используется квадрат (a2). Некоторые числа мы уже возводили в него (от 1 до 25). Значения больших чисел же можно искать тут:
*Для лучшего понимания примеры подсвечены голубым.
С левой стороны указаны десятки, а сверху — единицы. Т.е., для возведения в квадрат числа 24 ищем пересечение его десятка и единицы (2 — десяток, 4 — единица). Получаем показатель 576. Таким образом данная таблица степеней натуральных чисел может использоваться для возведения в квадрат цифр до 99.
Пример 3. Возводим большие значения в квадрат.
Задача. Найти 632.
Решение. В числе «63» 6 десятков и 3 единицы. Десятки у нас находятся с левой стороны, а единицы — в верхней строчке. Ищем нужные значения в таблице степеней по алгебре и находим число, находящееся на их пересечении.
Ответ. 3969.
Нет времени решать самому?
Наши эксперты помогут!
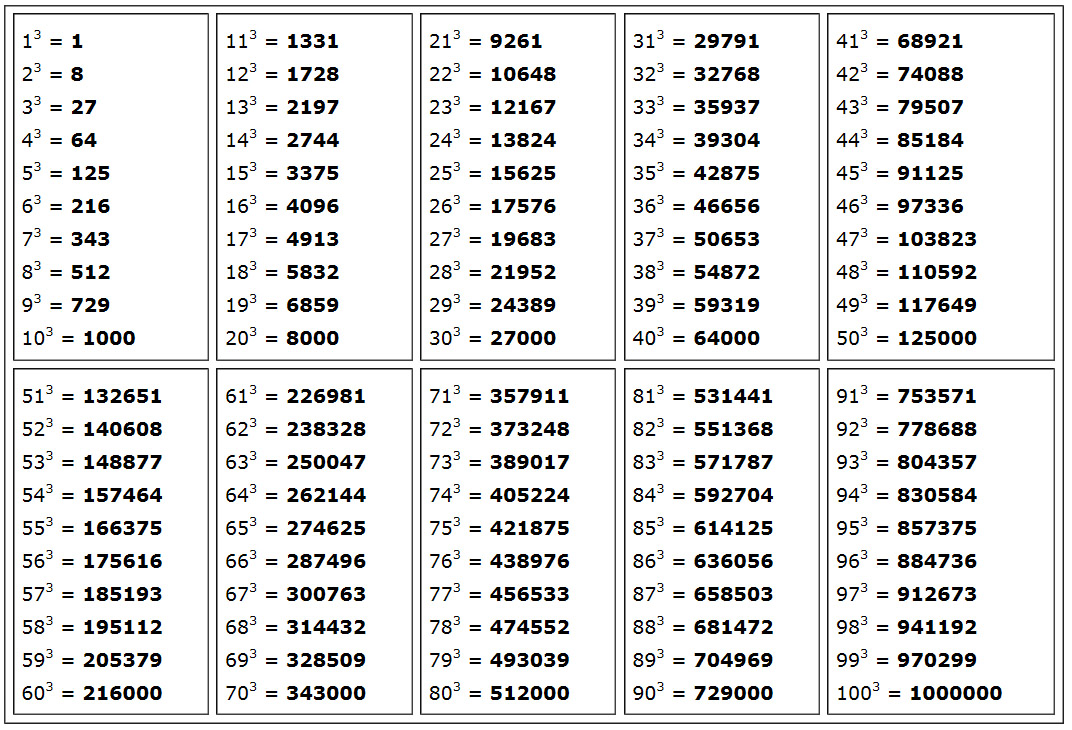
Таблица степеней чисел до 100 в кубе
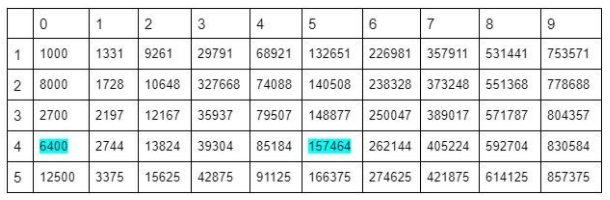
Часто в примерах требуется возвести двузначное число в куб. Сделать это будет проще со следующей таблицей:
*Для лучшего понимания примеры подсвечены голубым.
Пример 4. Работаем с таблицей натуральных степеней чисел в кубе.
Задача. Найти 453.
Решение. Делим число на десятки и единицы. Находим 4 десятка (левый столбец) и 5 единиц (верхняя полоса) и ищем значение их пересечения.
Ответ. 157464.
Пример 5. Вычисляем квадрат по таблице.
Задача. Найти 403.
Решение. Найти значение можно двумя способами. Первый — руководствуясь таблицей. 4 — десятки, 0 — единицы. Ищем пересечение этих цифр. Результат — 6400. Второй способ: возводим 4 в куб и прибавляем два нуля (т.к. 10 в кубе = 100). 43=64. Прибавляем «00» и получаем идентичный ответ: 6400.
Ответ. 6400.
Пользоваться таблицами степеней по математике несложно. Но только в том случае, если речь идет о небольших цифрах. В длинных примерах, состоящих из множества чисел в степенях, можно использовать онлайн калькуляторы. Это позволит избежать ошибок, которые могут быть вызваны просмотром не той ячейки.
Таблица степеней
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Существует множество таблиц значений степеней натуральных чисел. Привести их все не представляется возможным. Здесь мы приведем примеры некоторых таких таблиц и задачи на нахождение значений по таким таблицам.
Таблица степеней первых натуральных чисел
Приведем для начала таблицу для нахождения степеней натуральных чисел от $2$ до $12$ по степеням от $1$ до $10$ (таблица 1). Отметим, что мы не приводим степени числа $1$, потому что единица в любой степени будет равняться самой себе.
Находить по этой таблице значения надо следующим образом: В первом столбце находим число, степень которого нас интересует. Запоминаем номер этой строчки. Затем в первой сроке находим показатель степени и запоминаем найденный столбец. Пересечение найденной строки и столбца и даст нам ответ.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 1
Найти $8^7$
Решение.
Находим в первом столбце число $8$: получаем 8-ю строчку.
Находим в первой строке число $7$: получаем 8-й столбец.
Видим, что на их пересечении находится число $2097152$. Следовательно
$8^7=2097152$
Таблицы степеней натуральных чисел от $1$ до $100$
Также довольно популярны таблицы степеней от $1$ до $100$. Все их привести невозможно, поэтому мы здесь приведем для примера такие таблицы для квадратов и кубов таких натуральных чисел (таблица 2 и таблица 3).
«Таблица степеней» 👇
Эти таблицы напоминают всем известные таблицы умножения, поэтому, мы думаем, читателю не составит труда использование данных таблиц.
Пример 2
Найти
а) $76^2$.
б) $28^3$
Решение.
а) Данное значение находим в таблице $2$ в $8$ табличке:
$76^2=5776$
б) Данное значение находим в таблице $3$ в $3$ табличке:
$28^3=21952$
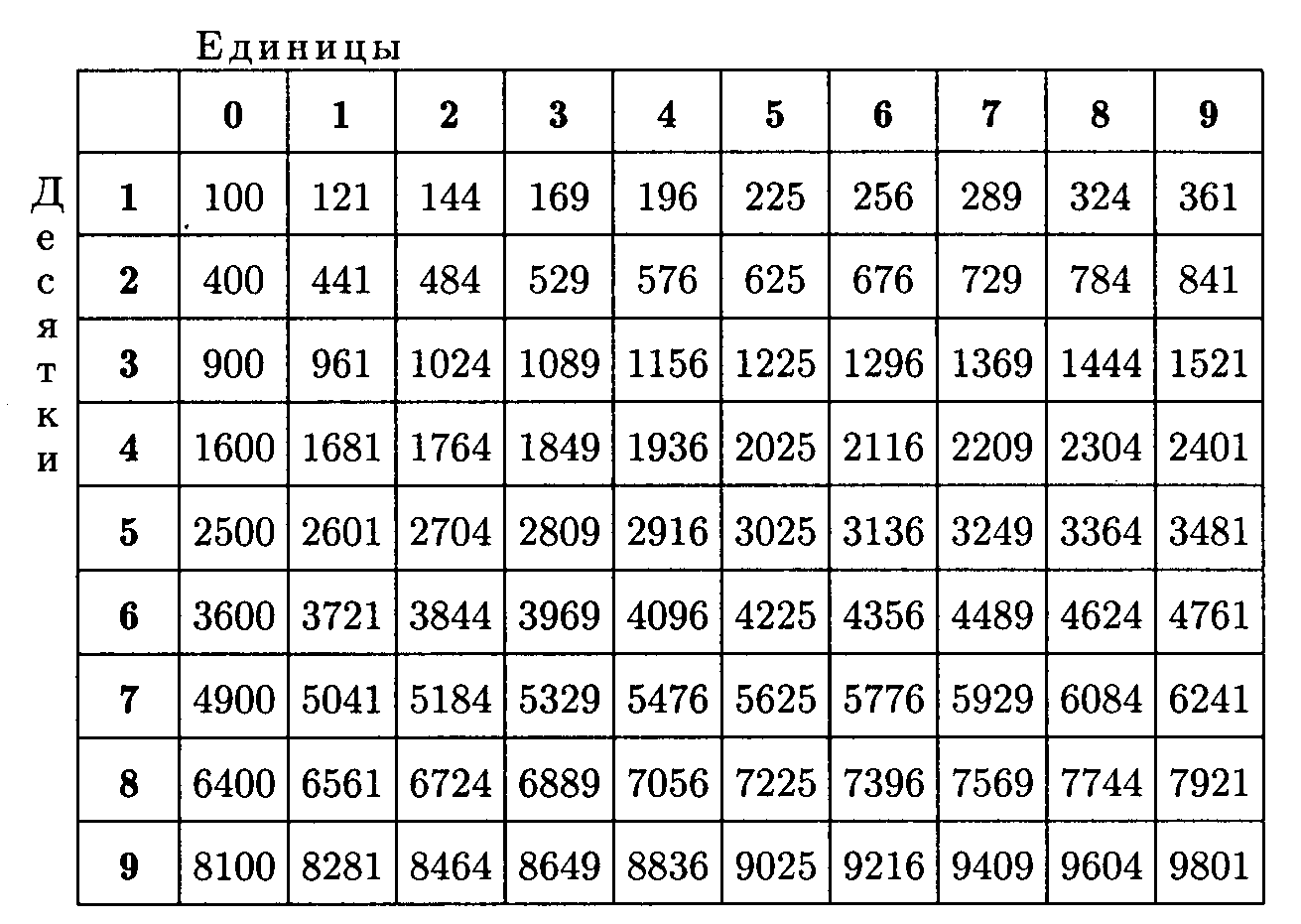
Таблица квадратов натуральных чисел от $10$ до $99$
Еще одной пользующейся популярностью таблицей является таблица квадратов чисел от $10$ до $99$ (таблица 4), то есть всех десятичных чисел.
Находить по этой таблице значения надо следующим образом: В первом столбце находим число десятков интересующего нас числа. Запоминаем номер этой строчки. Затем в первой сроке находим число единиц интересующего числа и запоминаем найденный столбец. Пересечение найденной строки и столбца и даст нам ответ.
Пример 3
Найти $37^2$
Решение.
Находим в первом столбце число $3$: получаем 4-ю строчку.
Находим в первой строке число $7$: получаем 8-й столбец.
Видим, что на их пересечении находится число $1369$. Следовательно
$37^2=1369$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 25.06.2022