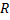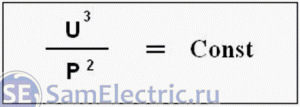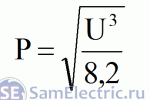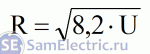Как найти сопротивление лампы 8 класс

Смешанное соединение проводников. Расчёт электрических цепей

Повторение. Факты про последовательное и параллельное соединение проводников.

1. При по­сле­до­ва­тель­ном со­еди­не­нии про­вод­ни­ков общее со­про­тив­ле­ние участ­ка равно сумме со­про­тив­ле­ний про­вод­ни­ков:

 

2. При по­сле­до­ва­тель­ном со­еди­не­нии про­вод­ни­ков силы тока в каж­дом из про­вод­ни­ков равны и равны общей силе тока на участ­ке цепи:

 

3. При по­сле­до­ва­тель­ном со­еди­не­нии про­вод­ни­ков сумма на­пря­же­ний равна об­ще­му на­пря­же­нию на участ­ке цепи:

 

4. При па­рал­лель­ном со­еди­не­нии про­вод­ни­ков общая про­во­ди­мость участ­ка равна сумме про­во­ди­мо­стей про­вод­ни­ков:

 

5. При па­рал­лель­ном со­еди­не­нии про­вод­ни­ков сумма сил токов равна общей силе тока на участ­ке цепи:

 

6. При па­рал­лель­ном со­еди­не­нии про­вод­ни­ков на­пря­же­ния в каж­дом из про­вод­ни­ков равны и равны об­ще­му на­пря­же­нию на участ­ке цепи:

 

Задача 1

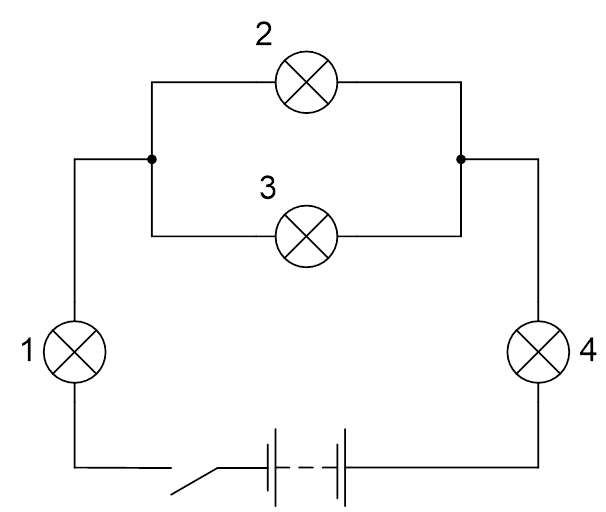
Че­ты­ре оди­на­ко­вые лампы под­клю­че­ны к ис­точ­ни­ку по­сто­ян­но­го на­пря­же­ния (см. Рис. 1). Опре­де­ли­те силу тока в каж­дой лампе, если на­пря­же­ние на ис­точ­ни­ке со­став­ля­ет 30 В.

Дано: ;

Найти: , , ,

Ре­ше­ние

Задача Че­ты­ре оди­на­ко­вые лампы под­клю­че­ны к ис­точ­ни­ку по­сто­ян­но­го на­пря­же­ния (см. Рис. 1). Опре­де­ли­те силу тока в каж­дой лампе, если на­пря­же­ние на ис­точ­ни­ке со­став­ля­ет 30 В

Рис. 1. Ил­лю­стра­ция к за­да­че

На ри­сун­ке 1 изоб­ра­же­на элек­три­че­ская цепь со сме­шан­ным со­еди­не­ни­ем про­вод­ни­ков: лампы 2 и 3 со­еди­не­ны па­рал­лель­но, а лампы 2 и 4 со­еди­не­ны по­сле­до­ва­тель­но с участ­ком цепи, со­сто­я­щим из ламп 2 и 3.

Про­во­ди­мость участ­ка цепи, со­сто­я­ще­го из ламп 2 и 3, равна:

 

Сле­до­ва­тель­но, со­про­тив­ле­ние этого участ­ка равно:

 

Так как лампы 1 и 4 со­еди­не­ны по­сле­до­ва­тель­но с участ­ком цепи, со­сто­я­щим из ламп 2 и 3, то общее со­про­тив­ле­ние ламп будет равно:

 

Со­глас­но за­ко­ну Ома, сила тока всей цепи равна:

 

Так как при по­сле­до­ва­тель­ном со­еди­не­нии про­вод­ни­ков силы тока в каж­дом из про­вод­ни­ков равны и равны общей силе тока на участ­ке цепи, то:

 

Необ­хо­ди­мо найти силу тока на лам­пах 2 и 3. Для этого вы­чис­лим на­пря­же­ние на участ­ке цепи, ко­то­рый со­сто­ит из ламп 2 и 3:

 

Так как лампы 2 и 3 со­еди­не­ны па­рал­лель­но, то на­пря­же­ния на этих лам­пах равны:

 

От­сю­да сила тока в каж­дой лампе равна:

 

 

Ответ:  ;  

Задача 2

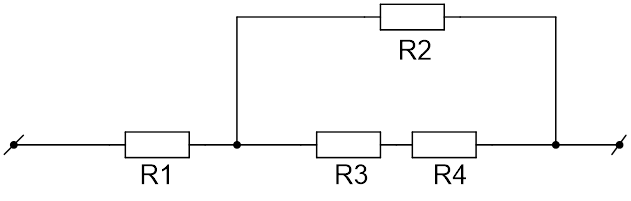
Уча­сток цепи, ко­то­рый со­сто­ит из че­ты­рёх ре­зи­сто­ров, под­клю­чён к ис­точ­ни­ку с на­пря­же­ни­ем 40 В (см. Рис. 2). Вы­чис­ли­те силу тока в ре­зи­сто­рах 1 и 2, на­пря­же­ние на ре­зи­сто­ре 3. Со­про­тив­ле­ние пер­во­го ре­зи­сто­ра равно 2,5 Ом, вто­ро­го и тре­тье­го – по 10 Ом, чет­вёр­то­го – 20 Ом.

Дано: ; ; ;

Найти: , ,

Ре­ше­ние

Задача Вы­чис­ли­те силу тока в ре­зи­сто­рах 1 и 2, на­пря­же­ние на ре­зи­сто­ре 3

Рис. 2. Ил­лю­стра­ция к за­да­че

Через ре­зи­стор  течёт такой же ток, как и через весь уча­сток (), сле­до­ва­тель­но, со­глас­но за­ко­ну Ома:

 

То есть для на­хож­де­ния  нужно вы­чис­лить со­про­тив­ле­ние (R) всего участ­ка цепи, ко­то­рый со­сто­ит из двух по­сле­до­ва­тель­но под­клю­чён­ных ча­стей, одна часть с ре­зи­сто­ром , дру­гая часть с ре­зи­сто­ра­ми :

 

Ре­зи­стор  со­еди­нён па­рал­лель­но ре­зи­сто­рам  и , сле­до­ва­тель­но:

 

Ре­зи­сто­ры  и  со­еди­не­ны по­сле­до­ва­тель­но, по­это­му:

 

 

 

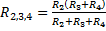
Сле­до­ва­тель­но, со­про­тив­ле­ние всей цепи равно:

 

Под­ста­вим дан­ное зна­че­ние в фор­му­лу для на­хож­де­ния тока в ре­зи­сто­ре :

 

Так как при па­рал­лель­ном со­еди­не­нии про­вод­ни­ков на­пря­же­ния в каж­дом из про­вод­ни­ков равны и равны об­ще­му на­пря­же­нию на участ­ке цепи, то:

 

От­сю­да:

 

 

 

При по­сле­до­ва­тель­ном со­еди­не­нии силы тока оди­на­ко­вы, по­это­му:

 

По­лу­чи­ли си­сте­му урав­не­ний:

 

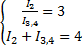
Решив эту си­сте­му по­лу­чим, что:

 

 

Так как  и  со­еди­не­ны по­сле­до­ва­тель­но:

 

На­пря­же­ние на ре­зи­сто­ре  равно:

 

Ответ: ;  ;  

Задача 3

Най­ди­те пол­ное со­про­тив­ле­ние цепи (см. Рис. 3), если со­про­тив­ле­ние ре­зи­сто­ров , , . Най­ди­те силу тока, иду­ще­го через каж­дый ре­зи­стор, если к цепи при­ло­же­но на­пря­же­ние 36 В.

Дано: ; ; ;

Найти: , , , , , , ;

Ре­ше­ние

Задача Най­ди­те пол­ное со­про­тив­ле­ние цепи, силу тока, идущего через каждый резистор

Рис. 3. Ил­лю­стра­ция к за­да­че

Ре­зи­сто­ры , ,  со­еди­не­ны по­сле­до­ва­тель­но, по­это­му со­про­тив­ле­ние на этом участ­ке равно:

 

Ре­зи­стор  под­клю­чён па­рал­лель­но участ­ку с ре­зи­сто­ра­ми , , , по­это­му со­про­тив­ле­ние на участ­ке с ре­зи­сто­ра­ми ,, ,  равно:

 

Ре­зи­сто­ры  и  со­еди­не­ны с участ­ком цепи с ре­зи­сто­ра­ми ,, ,  по­сле­до­ва­тель­но, то есть общее со­про­тив­ле­ние цепи равно:

 

Через ре­зи­стор  и   () нераз­ветв­лён­ной цепи течёт весь ток цепи, по­это­му:

 

По за­ко­ну Ома этот ток равен:

 

Общее на­пря­же­ние цепи будет со­сто­ять из на­пря­же­ний , так как ,,  со­еди­не­ны по­сле­до­ва­тель­но (, по­то­му что  и  па­рал­лель­ны):

 

 

Со­глас­но за­ко­ну Ома:

 

Ре­зи­сто­ры , ,  со­еди­не­ны по­сле­до­ва­тель­но, сле­до­ва­тель­но:

 

Ответ: ; ; ;   

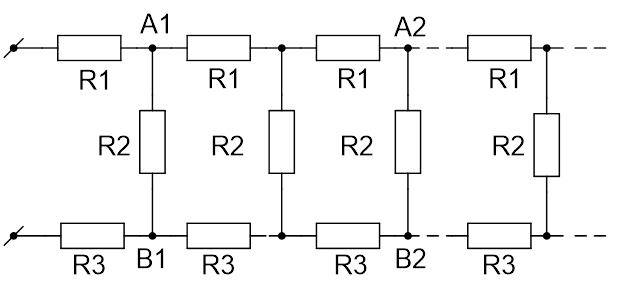
Разветвление: Задача на бесконечную электрическую цепь

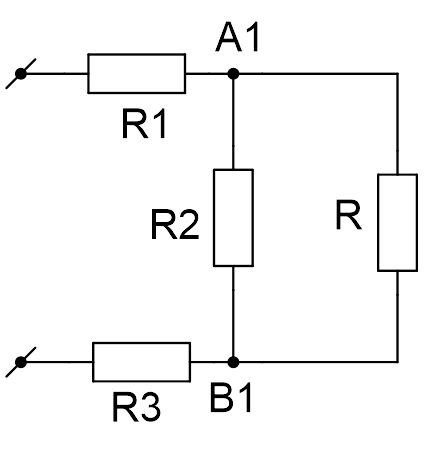
Най­ди­те со­про­тив­ле­ние R бес­ко­неч­ной цепи, по­ка­зан­ной на ри­сун­ке 4.

Задача на бесконечную электрическую цепь

Рис. 4. Ил­лю­стра­ция к за­да­че

Ре­ше­ние

По­сколь­ку рас­смат­ри­ва­е­мая в за­да­че цепь бес­ко­неч­на, уда­ле­ние одной «ячей­ки», со­сто­я­щей из ре­зи­сто­ров  и , не вли­я­ет на её со­про­тив­ле­ние. Сле­до­ва­тель­но, вся цепь, на­хо­дя­ща­я­ся пра­вее звена , тоже имеет со­про­тив­ле­ние R. Это поз­во­ля­ет на­ри­со­вать эк­ви­ва­лент­ную схему цепи (см. Рис. 5) и за­пи­сать для неё урав­не­ние.

эк­ви­ва­лент­ная схема цепи на бесконечную электрическую цепь

Рис. 5. Ил­лю­стра­ция к за­да­че

 

 

По­лу­чи­ли квад­рат­ное урав­не­ние от­но­си­тель­но R. Решая это урав­не­ние и от­бра­сы­вая от­ри­ца­тель­ный ко­рень (от­ри­ца­тель­но­го со­про­тив­ле­ния не су­ще­ству­ет), по­лу­ча­ем фор­му­лу для об­ще­го со­про­тив­ле­ния цепи:

 

Про­ана­ли­зи­ро­вав дан­ную фор­му­лу, можно за­ме­тить, что если , то общее со­про­тив­ле­ние цепи . То есть ре­зи­стор с малым со­про­тив­ле­ние  прак­ти­че­ски за­ко­ро­тит всю по­сле­ду­ю­щую бес­ко­неч­ную цепь.

Ответ:

Итоги

Мы рас­смот­ре­ли раз­лич­ные за­да­чи на сме­шан­ное со­про­тив­ле­ние про­вод­ни­ков, а также на рас­чёт элек­три­че­ских цепей.

Разветвление: Задача из ЕГЭ

Со­про­тив­ле­ние каж­до­го ре­зи­сто­ра в цепи (см. Рис. 6) равно 100 Ом. Уча­сток под­клю­чён к ис­точ­ни­ку по­сто­ян­но­го на­пря­же­ния вы­во­да­ми AиB. На­пря­же­ние на ре­зи­сто­ре  равно 12 В. Найти на­пря­же­ние между вы­во­да­ми схемы на участ­ке A–B(ва­ри­ан­ты от­ве­та: а) 12 В; б) 18 В; в) 24 В; г) 36 В.

Дано: ;

Найти:

Ре­ше­ние

Задача из ЕГЭ

Рис. 6. Ил­лю­стра­ция к за­да­че

Ре­зи­сто­ры  рас­по­ло­же­ны по­сле­до­ва­тель­но, зна­чит, силы тока на этих ре­зи­сто­рах равны:

 

Так как, по усло­вию, 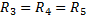, то и на­пря­же­ния на этих ре­зи­сто­рах будут равны:

 

Сле­до­ва­тель­но, общее на­пря­же­ния на участ­ке, со­сто­я­щем из ре­зи­сто­ров , будет равно:

 

Так как уча­сток с ре­зи­сто­ра­ми  со­еди­нён с участ­ком с ре­зи­сто­ра­ми  па­рал­лель­но, то на­пря­же­ния на этих участ­ках равны между собой и равны об­ще­му на­пря­же­нию на участ­ке A–B:

 

Ответ: г) 36 В

Дан­ную за­да­чу, как видим, можно ре­шить, не зная зна­че­ний со­про­тив­ле­ния, а зная толь­ко то, что они равны. Также эту за­да­чу можно ре­шить, зная зна­че­ние со­про­тив­ле­ний , даже если они не равны.

Вопросы к конспектам

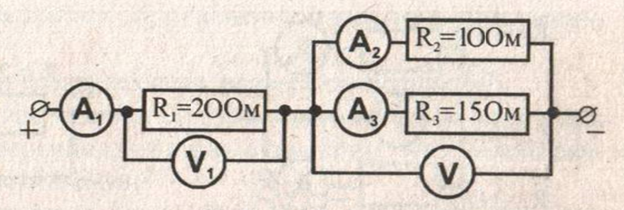
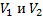
Уча­сток элек­три­че­ской цепи со­сто­ит из трех со­про­тив­ле­ний: ; ;  (см. Рис. 7). Опре­де­ли­те по­ка­за­ния вольт­мет­ров  и ам­пер­мет­ров , если ам­пер­метр  по­ка­зы­ва­ет силу тока 2 А.

Ил­лю­стра­ция к Домашнему заданию

Рис. 7. Ил­лю­стра­ция к за­да­че

Как нужно со­еди­нить че­ты­ре ре­зи­сто­ра, со­про­тив­ле­ния ко­то­рых 0,5 Ом, 2 ОМ, 3,5 Ом и 4 Ом, чтобы их общее со­про­тив­ле­ние было 1 Ом?

Источник

1) Для определения сопротивления лампы по мощности можно сначала найти силу тока I=P/U, затем найти сопротивление по закону Ома R=U/I или сразу по формуле R=U^2/P R=110^2/20=605 Ом.

2) При последовательном соединении сила тока в обоих лампах одинакова и мощности вычисляются по формуле P=I^2*R, то есть отношение мощностей равно отношению сопротивлений P2/P1=R2/R1. Найдем R2=U^2/P =220*220/50 = 968 Ом. Тогда Р2/Р1=968/605=1,6.

3) Ярче горит вторая лампа, так как она потребляет большую мощность, то есть имеет большее сопротивление.

Источник

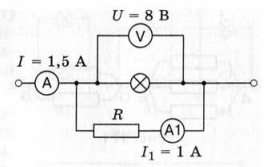
Рассчитайте силу тока в лампе и её сопротивление по схеме, изображённой на рисунке 174.
Задание рисунок 1
рис. 174

reshalka.com

ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Параллельное соединение проводников. Номер №1122

Решение

Дано:

I = 1,5 А;

U

л

=
8
В;

I

1

=
1
А.
Найти:

R

л

− ?

I

л

− ?
Решение:
При параллельном соединении сила тока в подводящих проводах равна сумме сил тока в лампе и проводнике:

I
=

I

1

+

I

л

;

I

л

=
I
−

I

1

;

I

л

=
1
,
5
−
1
=
0
,
5
А;
Напряжение на лампе и на проводнике равно напряжению сети, т.к. лампа и проводник соединены параллельно.

U

л

=

U

1

=
U
=
8
В;
Найдем сопротивление лампы по закону Ома:

R

л

=

U

I

л

;

R

л

=

8

0
,
5

=
16
Ом.
Ответ: 0,5 А; 16 Ом.

Источник

Перейти к содержимому

Для лампы накаливания мощностью сто пятьдесят ват и напряжением двести двадцать вольт необходимо определить величину сопротивления вольфрамовой нити накаливания при температуре двадцать пять градусов Цельсия. Известно, что температура накала нити лампы составляет две тысячи пятьсот градусов Цельсия. Температурный коэффициент сопротивления вольфрама 5,1×10-3град-1.

Дано: U=220 В; Р=150 Вт; t°1=25°C; t°2=2500°C; α=5,1×10-3град-1
Найти: R1-?

Решение

Запишем формулы для расчета величины сопротивления нити накаливания при комнатной и рабочей температуре

R_1=R_0(1+{alpha}{t^circ}_1),
R_2=R_0(1+{alpha}{t^circ}_2),

где R1 — сопротивление нити накаливания при температуре 25 градусов Цельсия;
R2 — сопротивление нити накаливания при температуре 2500 градусов Цельсия.

R_1/R_2={1+{alpha}{t^circ}_1}/{1+{alpha}{t^circ}_2},
R_1=R_2{{1+{alpha}{t^circ}_1}/{1+{alpha}{t^circ}_2}}.

Сопротивление нити накаливания при рабочей температуре определим из формулы

P={U^2}/R_2, тогда
R_2=U^2/P

Итоговая формула для расчета величины сопротивления нити накаливания при температуре 25 градусов Цельсия принимает вид

R_1={U^2/P}*{{1+{alpha}{t^circ}_1}/{1+{alpha}{t^circ}_2}}={220^2/150}*{{1+5,1*10^{-3}*25}/{1+5,1*10^{-3}*2500}}=26,5Ом.

Ответ: сопротивление вольфрамовой нити накаливания электрической лампы при температуре двадцать пять градусов Цельсия составляет двадцать шесть целых пять десятых Ом.

Источник

Решил
я
как-то
проверить
закон
Ома.
Применительно
к
лампе
накаливания.
Измерил
сопротивление
лампочки
Лисма
230
В 
60
Вт,
оно
оказалось
равным
59
Ом.
Я
было
удивился,
но
потом
вспомнил
слово,
которое
всё
объясняло
–

бареттер.

Дело
в
том,
что
сопротивление
вольфрамовой
нити
лампы
накаливания
сильно
зависит
от
температуры
(следствие
протекания
тока).
В
моем
случае,
если
это
бы
был
не
вольфрам,
а
обычный
резистор,
его
рассеиваемая
мощность
при
напряжении
230
Вольт
была
бы
P
=
U2/R
=
896.
Почти
900
Ватт!

Кстати,
именно
поэтому
производители
датчиков
с
транзисторным
выходом
рекомендуют
соблюдать
осторожность

при
подключении
датчиков.

Как
же
измерить
рабочее
сопротивление
нити
лампы
накаливания?
А
никак.
Его
можно
только
определить
косвенным
путем,
из
закона
знаменитого
Ома.
(Строго
говоря,
все
омметры
используют
тот
же
закон
–
прикладывают
напряжение
и
меряют
ток).
И
мультиметром
тут
не
обойдешься.

Используя
косвенный
метод
и
лампочку
Лисма
24
В
 с
мощностью
40
Вт,
я
составил
вот
такую
табличку:


Зависимость
сопротивления
нити
лампы
накаливания
от
напряжения

Напряжение 2 4 6 8 10 12 14 16
%
напряжения		 8.3 16.7 25.0 33.3 41.7 50.0 58.3 66.7
Ток 0.55 0.7 0.84 0.97 1.08 1.19 1.29 1.38
Сопротивление 3.6 5.7 7.1 8.2 9.3 10.1 10.9 11.6
Мощность 1.1 2.8 5.04 7.76 10.8 14.28 18.06 22.08 
(продолжение таблицы)
Напряжение 18 20 22

24		 26 28 30 32
%
напряжения		 75.0 83.3 91.7

100.0		 108.3 116.7 125.0 133.3
Ток 1.47 1.55 1.63

1.7		 1.77 1.84 1.92 2
Сопротивление 12.2 12.9 13.5

14.1		 14.7 15.2 15.6 16.0
Мощность 26.46 31 35.86

40.8		 46.02 51.52 57.6 64 
(Номинальные параметры выделены)

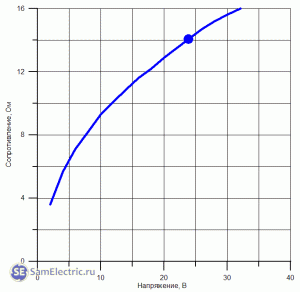
Как
видно
из
таблицы,
зависимость
сопротивления
лампочки
от
напряжения
нелинейная.
Это
может
проиллюстрировать
график,
приведенный
ниже.
Рабочая
точка
на
графике
выделена.

Сопротивление нити лампы накаливания

Сопротивление
нити
лампы
накаливания
в
зависимости
от
напряжения

Кстати,
сопротивление
подопытной
лампочки,
измеренное
с
помощью
цифрового
мультиметра
–
около
1
Ома.
Предел
измерения
–
200
Ом,
при
этом
выходное
напряжение
вольтметра
–
0,5
В.
Эти
данные
также
укладываются
в
полученные
ранее.

Зависимость
мощности
от
напряжения:

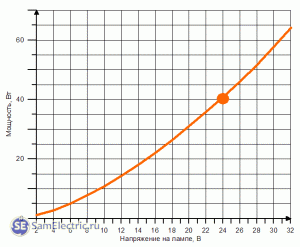
Зависимость мощности от напряжения

Зависимость
мощности
от
напряжения

Для
ламп
на
напряжение
230
В
на
основании
экспериментальных
данных
была
составлена
вот
такая
табличка:

Мощность
лампочки,

Вт

 25 40 60 75 100
R
холодной
нити,Ом		 150 90-100 60-65 45-50 37-40
R
горячей

нити,
Ом

 1930 1200 805 650 490
Rгор./Rхол. 12 12 13 13 12

Из
этой
таблицы
видно,
что
сопротивление
нити
лампы
накаливания
в
холодном
и
горячем
состоянии
отличается
в
12-13
раз.
А
это
значит,
что
во
столько
же
раз
увеличивается
потребляемая
мощность
в
первоначальный
момент.

Стоит
отметить,
что
сопротивление
в
холодном
состоянии
измерялось
мультиметром
на
пределе
200
Ом
при
выходном
напряжении
мультиметра
0,5
В.
При
измерении
сопротивления
на
пределе
2000
Ом
(выходное
напряжение
2
В)
показания
сопротивления
увеличиваются
более
чем
в
полтора
раза,
что
опять
же
укладывается
в
идею
статьи.

“Горячее”
сопротивление
измерялось
косвенным
методом.


UPD:
Сопротивление
нити
накаливания
люминесцентных
ламп

Дополнение
к
статье,
чтобы
получился
ещё
более
полный
материал.

Лампы
с
цоколем
Т8,
сопротивление
спирали
в
зависимости
от
мощности
:

10
Вт
–
8,0…8,2
Ом

15
Вт
–
3,3…3,5
Ом

18
Вт
–
2,7…2,8
Ом

36
Вт
–
2,5
Ом.

Сопротивление
измерялось
цифровым
омметром
на
пределе
200
Ом.


Формула
мощности
и
напряжения

Обновление
статьи
от
января
2018.
У
меня
на
блоге
появилась

статья
автора
Станислава
Матросова,
который
развил
тему
сопротивления
спирали
лампочки
с
теоретической
стороны.
Он
вывел
формулу,
согласно
которой:

Для
любой
лампы
накаливания
существует
параметр,
стабильный
в
широком
диапазоне
электрических
режимов. Этим
параметром
является
отношение
куба
напряжения
к
квадрату
мощности:

1. Лампа накаливания: отношение куба напряжения к квадрату мощности

Я
решил
на
основе
данных,
полученных
в
статье,
посчитать
эту
величину
в
Экселе.
Вот
что
у
меня
получилось:


U
P
U^3
P^2
Const
2 1,1 8 1,21 6,61157
4 2,8 64 7,84 8,163265
6 5,04 216 25,4016 8,503401
8 7,76 512 60,2176 8,502498
10 10,8 1000 116,64 8,573388
12 14,28 1728 203,9184 8,473978
14 18,06 2744 326,1636 8,412956
16 22,08 4096 487,5264 8,401596
18 26,46 5832 700,1316 8,329863
20 31 8000 961 8,324662
22 35,86 10648 1285,94 8,280327
24 40,8 13824 1664,64 8,304498
26 46,02 17576 2117,84 8,29902
28 51,52 21952 2654,31 8,270321
30 57,6 27000 3317,76 8,138021
32 64 32768 4096 8

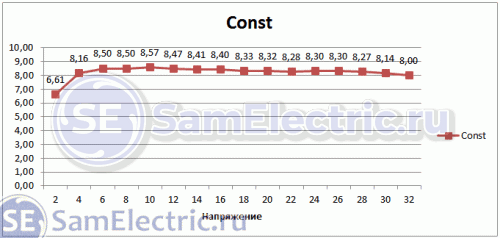
Действительно,
константа,
которая
с
некоторой
погрешностью
во
всём
диапазоне
равна
8,2±0,2.
Её
размерность
–
“Вольт
в
кубе
на
Ватт
в
квадрате”.

Константа для расчета лампы накаливания

Константа
для
расчета
лампы
накаливания
=
8,2

Низкое
значение
константы
в
начале
диапазона
объяснено
автором
в
приведенной
по
ссылке
статье.

Теперь,
зная
значение
этой
константы
(8,2),
можем
записать
формулу
зависимости
мощности
от
напряжения
лампочки
накаливания
40Вт
24В:

Зависимость мощности лампочки накаливания от напряжения

Зависимость
мощности
лампочки
накаливания
от
напряжения


Формула
для
сопротивления

Но
вернёмся
к
теме
статьи.
Проверим
вывод
Станислава
Матросова
о
том,
что
сопротивление
лампочки
пропорционально
корню
из
напряжения.
Из
предыдущих
выводов
можно
вывести
формулу
для
конкретной
лампочки
40Вт
24В:

Зависимость сопротивления от напряжения, формула для лампы накаливания

Зависимость
сопротивления
от
напряжения,
формула
для
лампы
накаливания

Теперь
проверим,
как
эта
формула
соотносится
с
полученными
мною
экспериментальным
данным
(см.
таблицу
в
начале
статьи).
Составим
такую
таблицу:

1.
Напря-

жение,
В

 2.
Норм.

напр.

 3.
Сопрот.,

Ом

 4.
Норм.

сопрот.

 5.
Корень

из
норм.

напряж.

 6.
Корень

из
напряж.

Х
Корень

из
Const
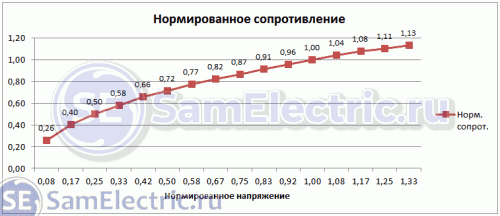
2 0,08 3,6 0,26 0,29 4,04
4 0,17 5,7 0,40 0,41 5,72
6 0,25 7,1 0,50 0,50 7,01
8 0,33 8,2 0,58 0,58 8,09
10 0,42 9,3 0,66 0,65 9,04
12 0,50 10,1 0,72 0,71 9,91
14 0,58 10,9 0,77 0,76 10,70
16 0,67 11,6 0,82 0,82 11,44
18 0,75 12,2 0,87 0,87 12,13
20 0,83 12,9 0,91 0,91 12,79
22 0,92 13,5 0,96 0,96 13,41
24 1,00 14,1 1,00 1,00 14,01
26 1,08 14,7 1,04 1,04 14,58
28 1,17 15,2 1,08 1,08 15,13
30 1,25 15,6 1,11 1,12 15,66
32 1,33 16 1,13 1,15 16,18

Таблица
требует
пояснений.
Чтобы
была
соблюдена
размерность,
я
нормировал
экспериментально
заданное
напряжение
(столбец
2)
и
рассчитанное
сопротивление
(столбец
4).

Колонка
5
–
это
корень
из
нормированного
напряжения,
и
видно,
что
значения
этой
колонки
отлично
совпадают
с
колонкой
4!

Но
давайте
вернемся
в
реальному
сопротивлению,
и
рассчитаем
его
по
приведенной
выше
формуле
(Зависимость
сопротивления
от
напряжения).
Это
–
6-я
колонка.
Хорошо
видно,
что
расчет
по
формуле
практически
идеально
совпадает
с
расчетом
из
экспериментальных
данных!

Зависимость сопротивления от напряжения

Зависимость
сопротивления
от
напряжения.
Квадратичная
зависимость.

Кто
хочет
проверить
мои
расчеты,
прикладываю
файл: •

Файл
с
расчетами
и
графиками
/
Файл
с
расчетами
и
графиками
к
статье
про
лампу
накаливания,
xlsx,
19.51
kB,
скачан:
1064
раз./

Всё,
учебник
физики
можно
переписывать!
;)

Кому
интересно
–
задачка

про
последовательное
подключение
двух
лампочек.

Понравилось?
Поставьте
оценку,
и
почитайте
другие
статьи
блога!


Загрузка…


Внимание!
Автор
блога
не
гарантирует,
что
всё
написанное
на
этой
странице
—
истина.

За
ваши
действия
и
за
вашу
безопасность
ответственны
только
вы!

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти длину по формуле гюйгенса
  • Как исправить innodb
  • Как найти генеральную доверенность
  • Как составить прогноз погоды по народным приметам
  • Как найти картинку похожую а мою фото

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии