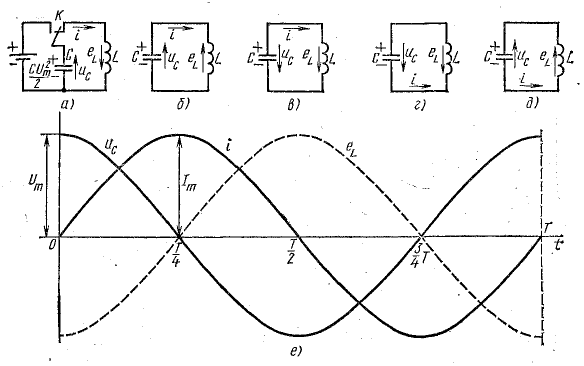
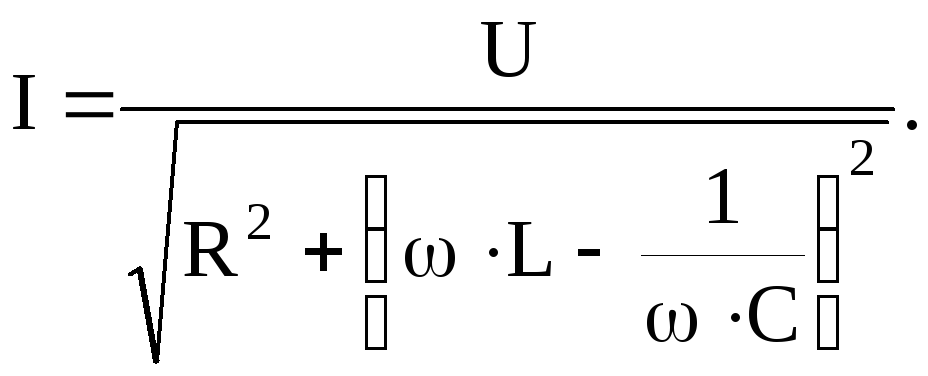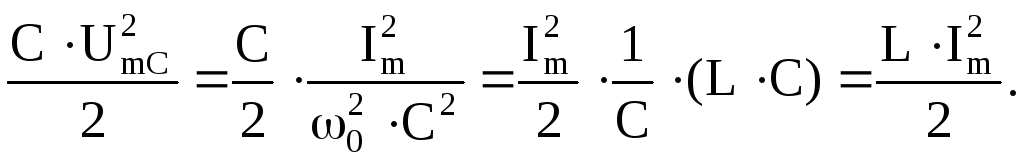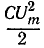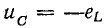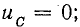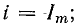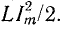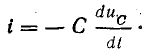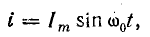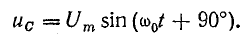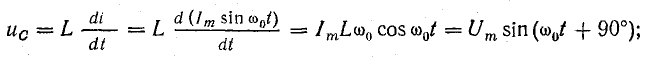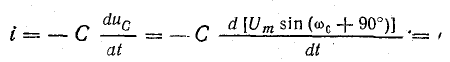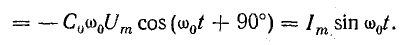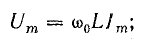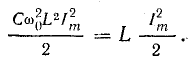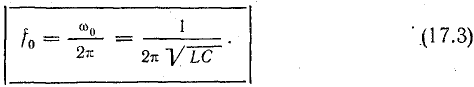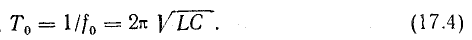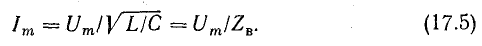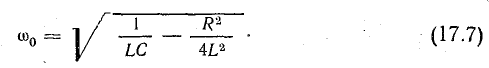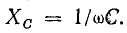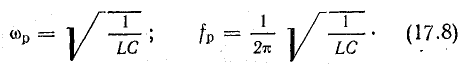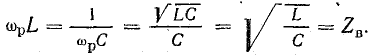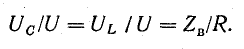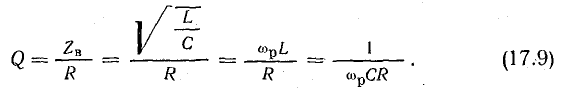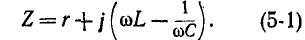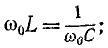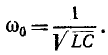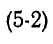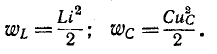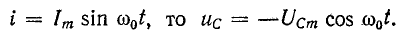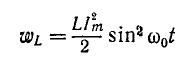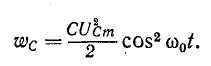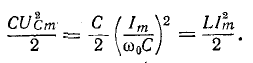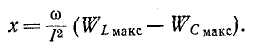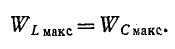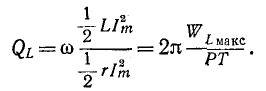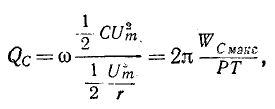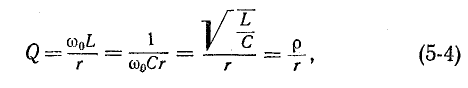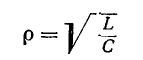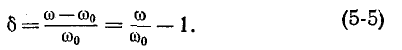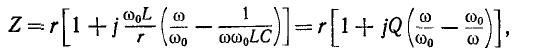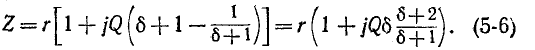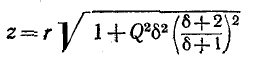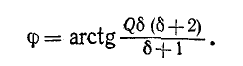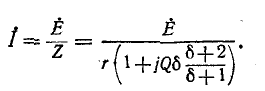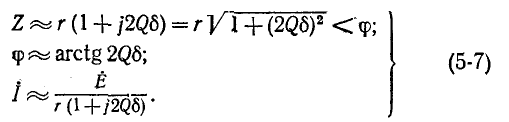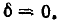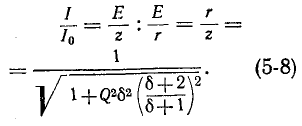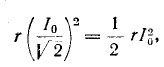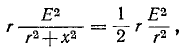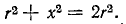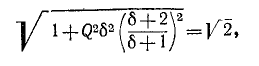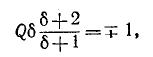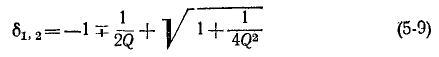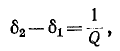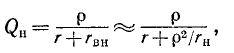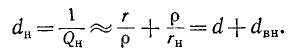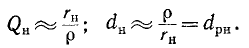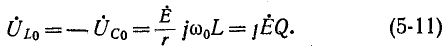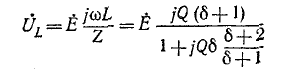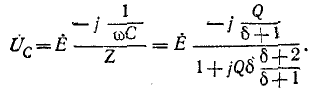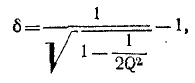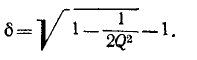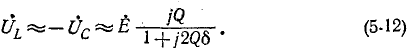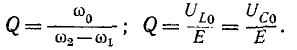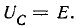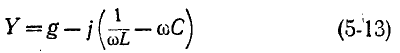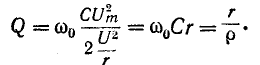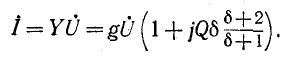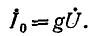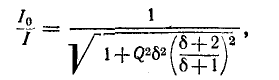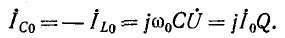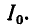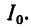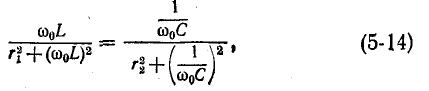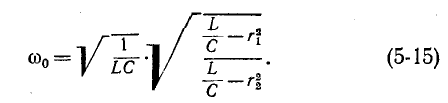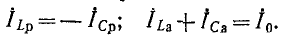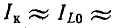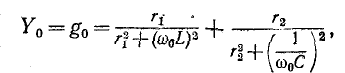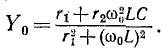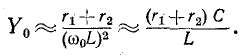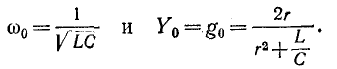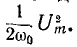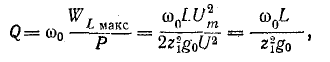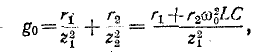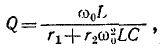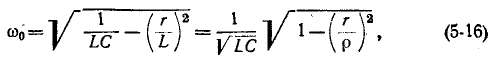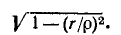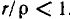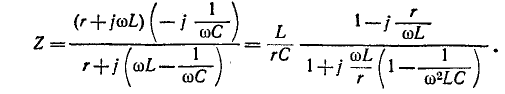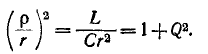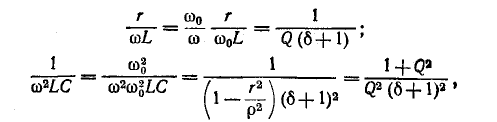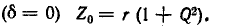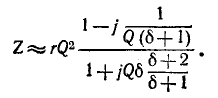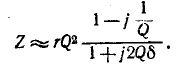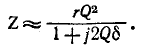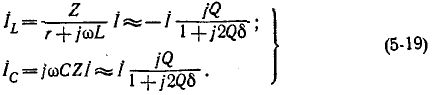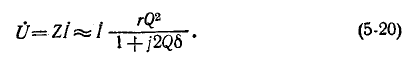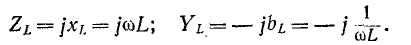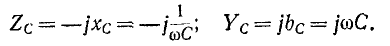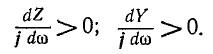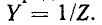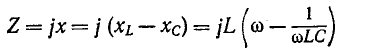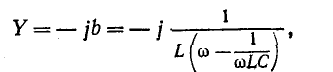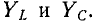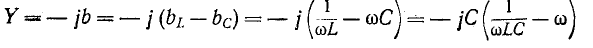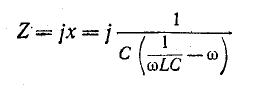Последовательный колебательный контур обозначение на схеме
Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно.
Идеальный последовательный колебательный контур
На схемах идеальный последовательный колебательный контур обозначается вот так:
где
L — индуктивность, Гн
С — емкость, Ф
Реальный последовательный колебательный контур
Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:
R — это суммарное сопротивление потерь катушки и конденсатора
L — собственно сама индуктивность катушки
С — собственно сама емкость конденсатора
Принцип работы последовательного колебательного контура
Генератор частоты и последовательный колебательный контур
Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:
Генератор (Ген)у нас будет выдавать синус.
Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.
А вот и сама схема в реальности:
Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R — это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно «прячется» внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.
Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта Uш , а также снимая осциллограмму с самого генератора UГЕН .
С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.
Влияние частоты генератора на сопротивление колебательного контура
В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.
Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.
Частота 200 Герц с копейками:
Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый
Добавляем частоту. 600 Герц с копейками
Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.
Добавляем частоту. 2 Килогерца
Сила тока стала еще больше.
3 Килогерца
Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.
4,25 Килогерц
Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.
И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.
Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.
Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.
Увеличиваем частоту еще больше
Сила тока начинает падать, а сдвиг фаз увеличивается.
22 Килогерца
74 Килогерца
Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.
Резонанс последовательного колебательного контура
Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:
Это явление носит название резонанса.
Не будем углубляться в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.
Как вы помните, если у нас сопротивление становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.
Формула Томсона (резонанса) для последовательного колебательного контура
Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора XL=XC , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:
Реактивное сопротивление конденсатора вычисляется по формуле:
Приравниваем обе части и вычисляем отсюда F:
В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.
Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.
Замеряем индуктивность катушки:
И замеряем нашу емкость:
Высчитываем по формуле нашу резонансную частоту:
У меня получилось 5, 09 Килогерц.
С помощью регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)
Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:
и конденсатор в 1000 пФ
Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.
Теперь небольшой прикол 
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!
Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:
Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Объяснение резонанса напряжения
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.
Добротность последовательного колебательного контура
Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:
Давайте посчитаем добротность в нашем случае.
Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала генератора частоты 2 Вольта.
А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.
Считаем по формуле добротности:
Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.
Есть также вторая формула для вычисления добротности.
где
R — сопротивление потерь в контуре, Ом
L — индуктивность, Генри
С — емкость, Фарад
Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.
Также хочу добавить пару слов о добротности. Добротность контура — это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.
Видео на тему «Как работает колебательный контур. Резонанс»:
Резюме
Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.
Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.
На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.
При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.
При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.
При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.
Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.
На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса — индуктивную составляющую тока.
В
цепи три последовательном соединении
R,
L, С
возможен резонанс напряжений. Такую
цель называют последовательным
колебательным контуром.
На
рис. 7.6 а
представлена эта цепь, а на рис. 7.6 б
приведена векторная диаграмма цеди для
случая резонанса напряжений.
Входное
комплексное сопротивление данной цепи
где
– реактивное сопротивление контура;R
– активное и
–полное
сопротивление (по модулю).
Угол
сдвига фаз между приложенным напряжением,
и токов запишется в виде

Условие
резонанса напряжений: х
=0
при
,
.
Угловая
резонансная частота
.
Отметим,
сто режим резонанса может наступит и
при изменении или индуктивности катушки
или ёмкости конденсатора; в этом случае
;
.
Условимся,
что будем рассматривать случай изменения
частоты источника питания.
Модуль
тока в цепи при заданном напряжений С:
В
режиме резонанса ток наибольший и равен
При
резонансе ток совпадает по фазе с
приложенным напряжением и это отмечено
на векторной диаграмме (рис. 7.6
б).
Характеристическое
сопротивление контура
равно
сопротивлению катушки индуктивностипри резонансе или сопротивлению
конденсатора при резонансе
(учтем,
что
):
;

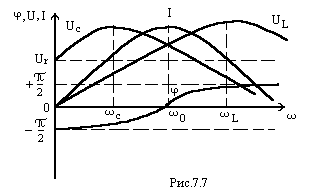
На
рис. 7.7 приведены частотные характеристики
последовательного контура, кривые
построены по формулам

;
;

Кривая
тока
имеет максимум при резонансной частоте
.
Если(постоянная ЭДС), ток равен нулю, так как
постоянный ток через конденсатор не
проходит. Если,
тогдаи
ток в цепи также стремится к нулю.
Напряжение
на конденсаторе UС
при
равно
напряжению генератора UГ.
Затем, по мере возрастания тока, напряжение
UС
вначале
увеличивается, достигает максимума при
частоте
,
а затем начинает уменьшаться. Максимум
напряжения на конденсаторе наступает
на частоте, которая меньше резонансной.
Это можно показать и аналитически, для
этого нужно определить максимум функцииUС
= UС()
из уравнения dUС/d
=
0.
При этом оказывается, что частота
максимального напряжения на конденсаторе
рассчитывается пo формуле
Напряжение
на катушке индуктивности
вначале
возрастает, становится равным напряжению
на конденсаторе при резонансе, затем
достигает максимума на частоте
более
высокой, чем резонансная частота. Это
же можно доказать аналитически, определив
максимум функция UL
= UL()
из уравнения dUL/d
=
0.
Частота
максимального напряжения на катушке
индуктивности может быть рассчитана
по формуле
Следует
иметь в виду, что
.
При
неограниченном увеличении частоты UL
стремится к напряжению UR.
Кривая
определяет сдвиг по фазе между током и
приложенным напряжением. При частотах,
меньших резонансной, в цепи преобладает
емкостное сопротивление и поэтому уголотрицательный, а после резонанса
сопротивлениеL,
больше, чем
,
и поэтому уголстанет положительным.
7.4. Энергетические соотношения при резонансе
Пусть
в последовательном колебательном
контуре R,
L, С
при резонансе ток равен
.
Тогда
напряжение на конденсаторе равно
.
Суммарная
энергия электрического поля конденсатора
и магнитного поля
катушки
индуктивности
равна
При
выводе этих формул учитывалось следующее
(при
):
При
резонансе суммарный запас энергии
магнитного поля и электрического поля
не меняется. Происходит перекачка
энергии от одного накопителя энергии
в другой. Уменьшение энергии электрического
поля конденсатора сопровождается
увеличением энергии магнитного поля
катушки индуктивности и наоборот.
Энергия, поступающая от источника
питания в любой промежуток времени,
целиком переходит в тепло. Поэтому
относительно источника питания цепь
эквивалентна одному активному
сопротивлению. При этом
;
.
Соседние файлы в папке Пособие по ТОЭ-1ч
- #
- #
- #
- #
- #
- #
- #
- #
Параллельный колебательный контур (рисунок 1) или последовательный колебательный контур (рисунок 2) могут использоваться в генераторах синусоидальных колебаний. Если в одной из этих схем зарядить конденсатор то он будет разряжаться заряжая катушку индуктивности, катушка разряжаясь будет заряжать конденсатор, этот процесс будет повторяться с определённым периодом T. Период это время одного колебания. Частота колебаний это величина обратная периоду. Разделив единицу на численное значение периода получим численное значение частоты.
Рисунок 1 — Параллельный колебательный контур
Рисунок 2 — Последовательный колебательный контур
Частота возникших колебаний называется собственной частотой колебаний контура для контуров изображённых на рисунках выше эта частота равна резонансной частоте этих контуров. Резонансная частота контура зависит от индуктивности L и ёмкости C её элементов, для колебательного контура (последовательного или параллельного) её можно найти по формуле:
Где L-индуктивность катушки контура, C-ёмкость конденсатора контура.
Если на параллельный или последовательный колебательный контур подавать переменное синусоидальное напряжение и изменять его частоту то будут меняться реактивные сопротивления элементов контура, если частота увеличивается то сопротивление конденсатора уменьшается а сопротивление катушки увеличивается и наоборот: если частота уменьшается то сопротивление конденсатора увеличивается а сопротивление катушки уменьшается, очевидно что есть такая частота при которой сопротивление катушки и конденсатора равны эта частота и есть резонансная. Сопротивление параллельного колебательного контура при этой частоте будет наибольшим (по сравнению с сопротивлениями этого контура при других частотах) а сопротивление последовательного колебательного контура при такой частоте будет наименьшим. Эти свойства контуров используют для построения фильтров например в полосно-пропускающем фильтре последовательно с нагрузкой ставиться последовательный контур и при подаче на это соединение (нагрузки и контура) переменного напряжения с резонансной частотой ток в нагрузке будет максимальным при других частотах ток будет меньше. Резонанс в параллельном контуре называют — резонансом токов, резонанс в последовательном контуре — резонансом напряжений. Можно простым способом определить каким будет сопротивление контура при резонансной частоте: например допустим что на параллельный колебательный контур подаётся постоянный ток, постоянный ток можно считать частным случаем переменного короче говоря постоянный ток это переменный с наименьшей возможной частотой, известно что при постоянном токе катушка действует как перемычка следовательно сопротивление контура будет равно нулю если резонансная частота не бесконечно мала (т.е. не постоянный ток) и сопротивление есть то оно больше нуля (т.е. сопротивления при постоянном токе) следовательно сопротивление параллельного колебательного контура на резонансной частоте максимальное а у последовательного контура наоборот. Зная то что конденсатор постоянный ток не пропускает, можно аналогично определить каким д.б. сопротивление последовательного контура на резонансной частоте. Выведем формулу для расчёта резонансной частоты зная то что при резонансе реактивные сопротивления элементов (катушки и конденсатора) контура равны:
Для расчёта резонансной частоты и периода колебаний колебательного контура с катушкой и конденсатором можно воспользоваться программой:
Содержание:
Резонанс в электрических цепях:
Явление резонанса можно наблюдать в любых колебательных системах, в том числе механических и электрических. Электрический резонанс возникает при определенных условиях в электрических цепях переменного тока, содержащих индуктивности и емкости.
Изучение электрического резонанса
Изучение электрического резонанса необходимо, так как это явление широко используется в технике электросвязи, а в установках сильного тока, где его возникновение специально не предусматривается, резонанс может оказаться опасным (могут возникнуть перенапряжения и пробой изоляции).
Колебательный контур
Для того чтобы понять резонансные явления, переходные процессы в электрических цепях переменного тока, которые рассматриваются далее, важно иметь представление о процессах в колебательном контуре, состоящем из идеальных катушки и конденсатора, т. е. в контуре без потерь.
Колебательный процесс в таком контуре заключается во взаимном преобразовании электрического и магнитного полей. При этом изменяется энергия полей, поэтому колебательный процесс в контуре с количественной стороны будем, как и раньше, характеризовать изменением энергии.
Ток и напряжение в колебательном контуре
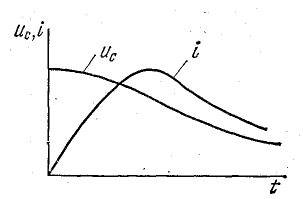
Предположим, что конденсатор с емкостью С получил от источника запас энергии
В первую часть периода (0 — T/4) конденсатор разряжается и в цепи существует ток. В это время в обособленной цепи конденсатор играет роль источника энергии (рис. 17.1, б). В начальный момент ток равен нулю, далее он увеличивается. Увеличение тока в цепи вызывает возникновение э. д. с. самоиндукции eL и накопление энергии в магнитном поле катушки. Э. д. с. самоиндукции уравновешивает напряжение на конденсаторе:
Напряжение на конденсаторе в процессе разрядки уменьшается, поэтому вызываемый в цепи ток растет все медленнее, соответственно с этим уменьшается и э. д. с. самоиндукции, которая пропорциональна скорости изменения тока. Таким образом, к концу разрядки конденсатора (
Рис. 17.1. К анализу колебательного контура
С этого момента ток начинает уменьшаться (но не прекращается), сохраняя свое направление. В следующую часть периода (от T/4 до T/2) направление тока сохраняется, потому что э. д. с. самоиндукции при уменьшении тока меняет свой знак, и роль источника энергии переходит к катушке. Уменьшающийся ток теперь является зарядным током конденсатора, заряжающегося в обратном направлении (рис. 17.1, в). Напряжение на конденсаторе увеличивается, уравновешивая теперь э. д. с. самоиндукции:
При увеличении напряжения на конденсаторе его зарядный ток уменьшается все быстрее, в результате чего э. д. с. eL увеличивается. Таким образом, к концу зарядки конденсатора напряжение на его обкладках достигает наибольшего значения, э. д. с. самоиндукции тоже максимальна, а ток становится равным нулю. Энергия магнитного поля снова перешла в энергию электрического поля . С этого момента рост э. д. с. самоиндукции прекращается и начинается ее уменьшение. Роль источника энергии снова переходит к конденсатору. Начинается третья часть периода (от Т/2 до 3T/4). В рассматриваемом процессе конденсатор второй раз становится источником энергии. Но по сравнению с первым он имеет обратную полярность, поэтому его разрядный ток изменяет направление и далее увеличивается. Снова энергия убывает в электрическом поле и накапливается в магнитном поле (рис. 17.1, г).
В момент времени t = 3T/4 напряжение на конденсаторе и э. д. с. самоиндукции становятся равными нулю, а ток — наибольшим. В последнем отрезке времени (от 3T/4 до Т) процесс протекает в том же порядке, что и во втором, но при обратном направлении тока (рис. 17.1, д).
В момент времени t = Т конденсатор заряжен в том же направлении и тем же количеством энергии, как и при t = 0. Ток переходит через нуль к положительным значениям и далее увеличивается. Процесс повторяется в порядке, рассмотренном ранее.
Характеристики колебательного контура
Энергетический процесс в колебательном контуре имеет периодический характер с периодом Т. Колебания в электрической цепи, не связанной с источником энергии, называют собственными или свободными.
Этот процесс рассмотрен по графикам изменения тока i, напряжения uC и э.д.с. eL, которые приняты синусоидальными функциями времени.
Для такого предположения имеется полное основание, так как эти величины взаимно связаны соотношением
Вместе с тем ток в контуре пропорционален скорости изменения заряда конденсатора, причем он увеличивается, когда конденсатор разряжается. Следовательно,
Такая взаимная связь переменных величин говорит о синусоидальном законе изменения тока и напряжения, но при наличии сдвига фаз между ними на 90°, т. е. при
Это можно проверить:
Величину ω0 в уравнениях тока и напряжения называют угловой частотой собственных колебаний в контуре. Найдем ее, используя равенство наибольшего количества энергии в конденсаторе и катушке:
и связь между амплитудами тока и напряжения:
Сокращая, получим
Частота собственных колебаний
Период собственных колебаний
Из равенства (17.1) вытекает еще одно важное соотношение
Величина, стоящая в знаменателе, имеет размерность сопротивления и называется волновым сопротивлением контура:
Колебательный контур с потерями энергии
Незатухающие колебания в контуре получаются в предположении, что потери энергии отсутствуют, т. е. R = 0.
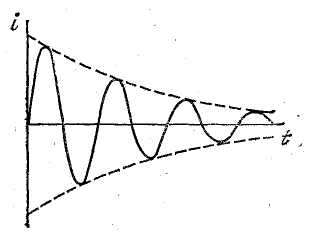
Если активное сопротивление контура не равно нулю, то запас энергии в контуре сокращается (энергия превращается в тепло), амплитуды тока и напряжения с каждым периодом убывают, как показано на рис. 17.2.
Более детальное исследование колебательного контура показывает, что частота собственных колебаний зависит от активного сопротивления:
При R = 0 это выражение совпадает с (17.2).
При 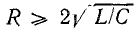
Рис. 17.2. График изменения тока в колебательном контуре с потерями
Рис. 17.3. Апериодический разряд конденсатора на катушку индуктивности
Резонанс напряжений
При рассмотрении различных режимов электрических цепей был отмечен случай равенства реактивных сопротивлений ХL = ХC при последовательном соединении элементов, содержащих индуктивность и емкость.
В этом случае электрическая цепь находится в режиме резонанса напряжений, который характеризуется тем, что реактивная мощность цепи равна нулю, ток и напряжение совпадают по фазе.
Условие возникновения резонанса
Резонанс напряжений возникает при определенной для данной цепи частоте источника энергии (частоте вынужденных колебании), которую называет резонансной частотой ωр.
При резонансной частоте, как будет показано далее, 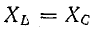
Режим электрической цепи при последовательном соединении участков с индуктивностью и емкостью, характеризующийся равенством индуктивного и емкостного сопротивлений, называют резонансом напряжений.
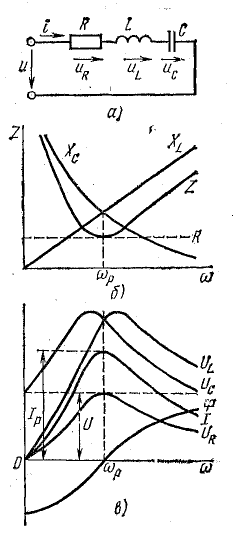
Резонанс напряжений рассмотрим, сначала на схеме идеализированной цепи (рис. 17.4, а), в которой последовательно с резистором R включены идеальные (без потерь) катушка L и конденсатор С.
Рис. 17.4. К вопросу о резонансе напряжений
Реактивные сопротивления ХL и ХC (рис. 17.4, б) зависят от частоты вынужденных колебаний ω:
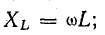
Приравнивая реактивные сопротивления и учитывая, что ω = ωр, получим
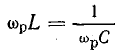
Отсюда резонансная частота
В данном случае выражение для резонансной частоты совпадает с формулой (17.3) для частоты собственных колебаний в контуре без потерь.
Основные соотношения между величинами, характеризующими режим электрической цепи и энергетические процессы. Нужно отметить, что в неразветвленной цепи обмен энергией между катушкой и конденсатором совершается через источник энергии, который восполняет потери энергии в активных сопротивлениях.
Резонансные кривые
Резонанс напряжений в цепи можно установить двумя путями: 1) изменением параметров L и С (одного из них или обоих вместе) при постоянной частоте источника или 2) изменением частоты источника энергии при постоянных L и С.
В связи с этим большой практический интерес представляют зависимости напряжений и токов на отдельных элементах цепи от частоты. Эти зависимости называют резонансными кривыми (рис. 17.4, в).
Реактивные сопротивления с изменением частоты меняются, как показано на рис. 17.4, б. При увеличении частоты ХL увеличивается пропорционально частоте, а ХC уменьшается по закону обратной пропорциональности.
Соответственно полное сопротивление Z цепи при резонансной частоте ωр оказывается наименьшим, равным активному сопротивлению R; при частоте 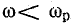
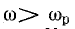
Такая зависимость полного сопротивления от частоты определяет характер изменения тока при постоянном напряжении в цепи (рис. 17.4, в). При 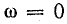
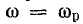
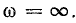
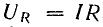
Напряжение на конденсаторе UC при 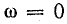
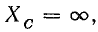
Индуктивное напряжение 

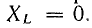
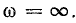
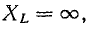
При частотах, меньших резонансной, реактивное сопротивление цепи имеет емкостный характер (отрицательно), поэтому и угол сдвига фаз в цепи отрицательный. Уменьшаясь с ростом частоты, он становится равным нулю при резонансе 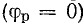
Добротность контура
При резонансе напряжений отношение напряжения на индуктивности или емкости к напряжению, приложенному к цепи (напряжению источника), равно отношению волнового сопротивления к активному. Действительно, при резонансе сопротивления реактивных элементов
Поэтому
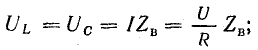
Из этого выражения следует, что при 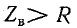
Такое превышение может оказаться значительным, если реактивные сопротивления много больше активного, и изоляция катушки или конденсатора может быть пробита. На практике подобный случай возможен, если на конце кабельной линии включается приемник, обладающий индуктивностью.
В радиотехнике качество резонансного контура считается тем выше, чем больше отношение 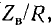
Чем меньше мощность потерь энергии в контуре (этому соответствует меньшая величина R), тем больше добротность контура.
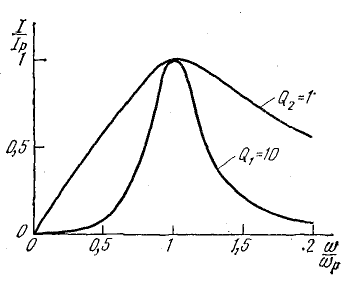
Большей величине добротности соответствует больший ток Iр при резонансе и более острая резонансная кривая.
На рис. 17.5 показаны две резонансные кривые тока, построенные в относительных единицах при двух величинах добротности. По горизонтальной оси отложены отношения изменяющейся частоты источника энергии к резонансной частоте ω/ωр, а по вертикальной —отношения тока при данной частоте к току при резонансной частоте I/Iр.
Рис. 17.5. Резонансные кривые при двух значениях добротности контура
Все рассуждения о резонансе напряжений в идеализированной цепи можно распространить и на цепи, содержащие последовательно соединенные катушку и конденсатор с потерями. Как известно, реальные катушки и конденсатор могут быть представлены схемами последовательного соединения активного и реактивного сопротивлений (рис. 17.5). Активные сопротивления катушки и конденсатора можно рассматривать как часть общего активного сопротивления цепи R, тогда схема на рис. 17.4, а будет пригодна и в этом случае.
Резонанс в электрических цепях
Резонансные (колебательные) цепи:
Резонансными или колебательными цепями называются электрические цепи, в которых могут возникать явления резонанса напряжений или токов.
Резонанс представляет собой такой режим пассивной электрической цепи, содержащей индуктивности и емкости, при котором реактивное сопротивление и реактивная проводимость цепи равны нулю; соответственно равна нулю реактивная мощность на выводах цепи.
Резонанс напряжения наблюдается в электрической цепи с последовательным соединением участков, содержащих индуктивности и емкости. Неразветвленная цепь, состоящая из последовательно соединенных элементов r, L и С, рассмотренная, представляет собой один из простейших случаев такой цепи. В радиотехнике ее называют последовательным колебательным контуром.
При резонансе напряжений индуктивное сопротивление одной части цепи компенсируется емкостным сопротивлением другой ее части, последовательно соединенной с первой. В результате реактивное сопротивление и реактивная мощность на выводах цепи равны нулю.
В свою очередь резонанс токов наблюдается в электрической цепи с параллельным соединением участков, содержащих индуктивности и емкости. Один из простейших примеров такой цепи, состоящей из параллельно соединенных элементов r, L и С. В радиотехнике такую цепь называют параллельным колебательным контуром.
При резонансе токов индуктивная проводимость одной части цепи компенсируется емкостной проводимостью другой ее части, параллельно соединенной с первой. В результате реактивная проводимость и реактивная мощность на выводах цепи равны нулю.
Частоты, при которых наблюдается явление резонанса, называются резонансными частотами.
Исследование резонансных режимов в электрических цепях заключается в нахождении резонансных частот,
зависимостей различных величин от частоты
Резонансные цепи очень широко применяются в электротехнике и представляют собой неотъемлемую часть всякого радиотехнического устройства. Изучению явления резонанса, свойств и частотных характеристик простейших резонансных цепей посвящена данная глава.
Последовательный колебательный контур. Резонанс напряжений
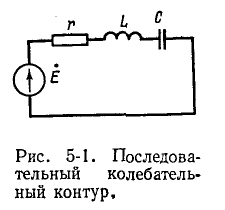
Резонансная цепь с последовательным соединением r, L и С (рис. 5-1) является простейшей цепью для изучения явления резонанса напряжений и подробно рассматривается ниже. Комплексное сопротивление такой цепи зависит от частоты:
Резонанс напряжений наступает при частоте 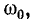
отсюда
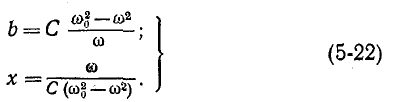
Мгновенные энергии выражаются формулами:
Если принять
Поэтому
и
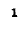
Максимальные значения этих энергий равны друг другу, так как
Это следует и из того, что реактивное сопротивление цепи, содержащей индуктивность и емкость, при любой схеме соединений пропорционально разности максимальных значений энергии, запасаемой в магнитном и электрическом полях:
Поэтому условию резонанса (х = 0) соответствует равенство
Мгновенные значения 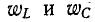
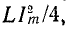
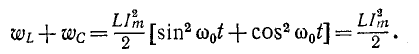
В рассматриваемом случае (резонанс напряжений, рис. 5-1) в цепи не происходит обмена энергии между источником и реактивными элементами цепи, а вся электрическая энергия, поступающая от источника, расходуется в сопротивлении r.
Мы уже встречались с понятием добротности индуктивной катушки 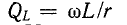
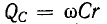
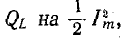
Здесь 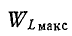
Аналогично рассуждая, т. е. умножив и разделив выражение 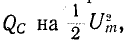
где 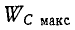
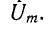
В случае резонансной цепи также пользуются понятием добротности цепи, подразумевая под этим в общем случае величину
здесь 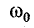
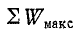
Знак 
Для схемы рис. 5-1 на основании (5-3) получаем:
где
называется характеристическим (а также волновым) сопротивлением резонансного контура.
Условимся называть относительной расстройкой частоты по отношению к резонансной
частоте контура величину
Сопротивление контура согласно (5-1) и с учетом (5-2) и (5-4)
откуда, используя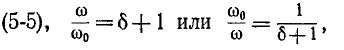
Следовательно, полное сопротивление цепи
и угол
Ток в цепи
При частоте, близкой к резонансной,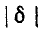
Выражения (5-7) практически достаточно точны при 
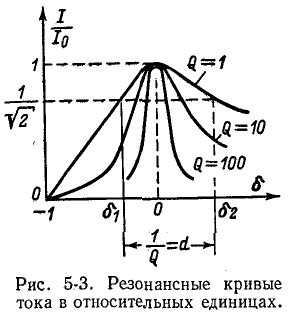
На рис. 5-2 кривые даны в относительных значениях: по оси абсцисс отложена относительная расстройка частоты 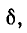
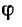
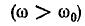
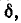
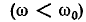
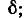
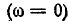
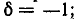
Полное сопротивление цепи минимально при резонансе напряжений при этом ток в цепи достигает своего максимального значения
На рис. 5-3 изображены резонансные кривые тока в относительных значениях: по оси абсцисс, как и на предыдущих графиках, отложены значения 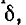
Чем выше добротность цепи Q, тем острее резонансные кривые. Таким образом, величина Q характеризует остроту резонансной кривой («остроту настройки»); согласно (5-3) чем больше отношение максимума энергии поля реактивного элемента к количеству теплоты, рассеиваемой за один период в резонансном контуре, тем острее резонансная кривая.
Резонансные кривые были построены здесь в зависимости от относительной расстройки частоты 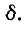
вывести расчетные выражения и построить резонансные кривые в зависимости от 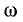
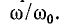
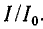
Полосу частот вблизи резонанса, на границах которой ток снижается до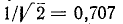
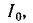
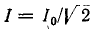
т. е. составляет половину мощности, расходуемой при резонансе. Поэтому полосу пропускания характеризуют как полосу, границы которой соответствуют половине максимальной мощности. На границах полосы пропускания резонансного контура активное и реактивное сопротивления равны 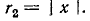
что дает
Соответственно и фазовый сдвиг между напряжением на выводах цепи и током составляет 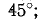
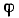
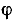
На основании (5-8) условие для границы полосы пропускания записывается в следующем виде:
или
откуда
(знак минус перед корнем, получающийся в результате решения квадратного уравнения, опускается, как не имеющий смысла). Индексы 1 и 2 и соответственно знаки минус и плюс в выражении (5-9) относятся к границам ниже и выше резонанса.
По определению полоса пропускания резонансного контура находится из условия
или
Величина d, обратная добротности контура, называется затуханием контура.
При достаточно высокой добротности резонансного контура 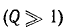
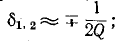
В радиотехнических устройствах к одному из реактивных элементов колебательного контура, например емкости, подключается нагрузка в виде сопротивления 
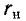
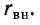
Так как обычно 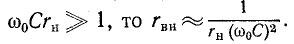
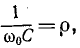
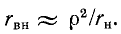
Таким образом, добротность нагруженного контура равна:
а затухание увеличивается на вносимое затухание
Если вносимое сопротивление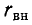
Внутреннее сопротивление источника э. д. с. 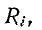
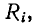
контура. Поэтому с точки зрения сокращения полосы пропускания последовательного колебательного контура выгоден источник напряжения с малым внутренним сопротивлением.
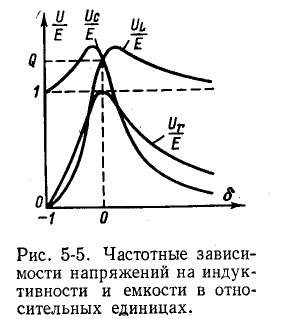
В условиях, близких к резонансу, напряжения на индуктивности и емкости могут быть весьма велики, что необходимо учитывать во избежание повреждения изоляции.
На рис. 5-4 показана векторная диаграмма тока и напряжений при резонансе. Напряжения на реактивных элементах при резонансе определяются из выражения
При Q > 1 эти напряжения превышают напряжение U — Е, приложенное к резонансному контуру. Однако значения, получаемые на основании (5-11), не являются максимальными: максимум напряжения 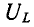
несколько выше (правее), а максимум Uc — ниже (левее) резонансной частоты (рис. 5-5).
Напряжение на индуктивности 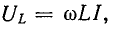
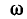
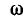
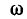
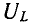
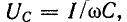
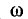
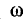
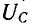
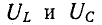
Эго также вытекает из анализа следующих ниже выражений, полученных с учетом (5-5) и (5-6):
и
Напряжение 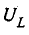
а напряжение
Пренебрегая 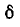
Возвращаясь к определению понятия добротности рассматриваемой резонансной цепи, мы видим, что наряду с формулами (5-3) и (5-4) добротность цепи характеризуется выражениями (5-10) и (5-11), а именно:
Последняя формула показывает, что добротность рассматриваемой цепи определяется как кратность перенапряжения на L и С при резонансной частоте.
Выше была рассмотрена неразветвленная электрическая цепь с последовательно соединенными r, L н С. Для исследования явления резонанса в более сложных разветвленных цепях, где резонанс напряжений может возникать на одной или нескольких частотах, наряду с аналитическим методом расчета, иллюстрированным выше, целесообразно также пользоваться методом геометрических мест.
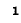
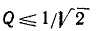
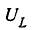
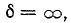
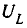
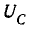
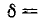

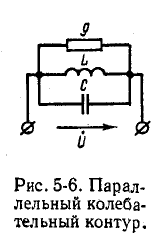
Параллельный колебательный контур и резонанс токов
Явление резонанса токов удобно изучать применительно к электрической цепи с параллельно соединенными r, L и С (рис. 5-6), так как при этом можно непосредственно воспользоваться результатами, полученными в предыдущем параграфе.
Действительно, выражение для комплексной проводимости такой цепи
по своей структуре аналогично выражению (5-1), причем резонансная частота определяется согласно (5-2).
Добротность резонансной цепи на основании (5-3)
По аналогии с предыдущим выражение (5-13) приводится к виду:
Сравнивая полученный результат с (5-6), убеждаемся в том, что выражение Y/g для схемы рис. 5-6 имеет тот же вид, что и выражение 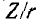
Поэтому кривые рис. 5-2 применимы и в данном случае: кривые рис. 5-2, а выражают зависимость от 6 Отношения y/g, а кривые рис. 5-2, б — зависимость угла —
Кривые рис. 5-2, а показывают, что при резонансе токов полная проводимость цепи минимальна, т. е. входное сопротивление достигает максимума.
При заданном напряжении 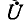
Этот ток достигает минимума при резонансной частоте, так как при этом
Следовательно, отношение. токов 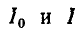
правая часть которого полностью совпадает с (5-8).
В связи с этим резонансные кривые рис. 5-3 выражают применительно к схеме рис. 5-6 зависимость
В случае резонанса токов токи в индуктивном и емкостном элементах схемы рис. 5-6 равны и противоположны по знаку:
Полученное выражение показывает, что добротность рассматриваемой цепи определяется как кратность токов в L и С по отношению к суммарному току
При Q > 1 эти токи превышают
Если параллельный колебательный контур питается от источника тока с внутренним сопротивлением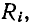
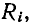
Для схемы рис. 5-6 при резонансе токов остается в силе вывод, сделанный в предыдущем параграфе о непрерывном обмене энергией между индуктивным и емкостным элементами при резонансе напряжений.
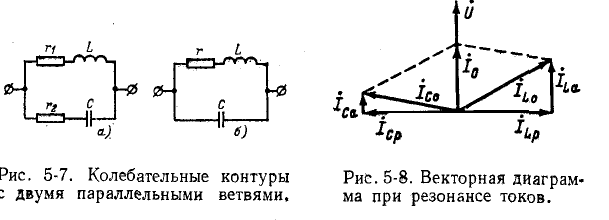
Схема рис. 5-6 является идеализированной, так как она не учитывает активных потерь в ветвях L и С. Поэтому рассмотрим другие схемы,’приняв во внимание активные сопротивления в ветвях L и С (рис. 5-7, а и б).
Условие резонанса токов для схемы рис. 5-7, а записывается в виде равенства реактивных проводимостей:
Откуда
Явление резонанса возможно при этом только в случае, если подкоренное выражение (5-15) имеет положительный
знак или, что то же, величины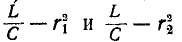
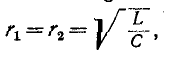
.
На рис. 5-8 показана векторная диаграмма при резонансе токов в цепи рис. 5-7, а. Токи в индуктивной и емкостной ветвях слагаются из активных 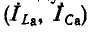
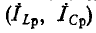
Чем меньше 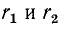
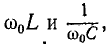
к 
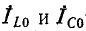
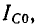
При резонансе вся цепь имеет только активную проводимость
откуда с учетом (5-14)
Для колебательного контура с малыми потерями можно пренебречь слагаемым 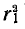
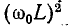
что 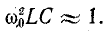
При 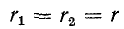
Кроме того, если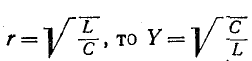
частоте (резонанс в такой цепи называют «безразличным» резонансом).
Легко убедиться в том, что и в. случае резонансной цепи с двумя параллельными ветвями (см. рис. 5-7) соблюдается условие 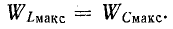
умножить обе части уравнения (5-14) на
Выше отмечалось, что в схеме с параллельно соединенными r, L и С (см. рис. 5-6) полная проводимость всей цепи имеет минимум при резонансной частоте.
Для схемы рис. 5-7, б нетрудно показать, что при изменении частоты о) или индуктивности L минимум полной проводимости цепи, а также минимум общего тока наступают не при резонансной частоте. В том же случае, когда переменным параметром является емкость С, проводимость и общий ток достигают минимума при резонансе токов.
Добротность параллельного колебательного контура рис. на основании (5-3) равна:
но
откуда
где резонансная частота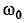
Часто в ветви с емкостью сопротивлением 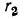
Рассмотрим этот случай (см. рис. 5-7, б).
Резонанасная частота такого контура согласно (5-15)
а добротность цепи в соответствии с полученным выше выражением
Из сопоставления (5-16) и (5-2) видно, что при одних и тех же параметрах r, L и С резонансные частоты для схем рис. 5-1 и 5-7, б отличаются множителем
При 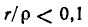
Общее сопротивление колебательного контура (см. рис, 5-7, б)
На основании соотношений (5-16) и (5-17) можно получить:
Учитывая также соотношения
получаем выражение для сопротивления колебательного контура:
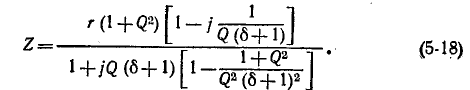
При резонансной частоте
В тех случаях, когда 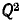
В режиме, близком к резонансу, когда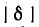
При высокой добротности колебательного контура
Приэтом токи в ветвях
Здесь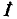
Напряжение на выводах цепи 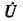
Приближенные выражения (5-19) и (5-20) аналогичны при заданном Q выражениям(5-12) и (5-7), выведенным для цепи рис. 5-1, при условии замены напряжений токами и обратно. Поэтому кривые сопротивлений, токов и напряжений, соответствующие схеме рис. 5-1, в известном масштабе приближенно выражают проводимости, напряжения и токи в схеме рис. 5-7, б.
Следует обратить внимание на то, что в схеме рис. 5-6 мгновенная мощность в цепи при резонансе токов равна мгновенной мощности, расходуемой в сопротивлении r; в схемах с двумя параллельными ветвями (рис. 5-7) мгновенная мощность на выводах цепи отлична от мгновенной мощности, расходуемой в сопротивлениях ветвей. Например, в тот момент, когда ток, входящий в цепь, проходит через нулевое значение, мгновенная мощность на выводах цепи равна нулю; в этот момент токи в ветвях, сдвинутые по фазе относительно суммарного тока цепи, отличны от нуля и поэтому мгновенная мощность, расходуемая в сопротивлениях ветвей, также не равна нулю. Объясняется это тем, что в схемах ~рис. 5-7, а и б энергия, накапливаемая реактивными элементами, периодически преобразуется частично в теплоту (в сопротивлениях ветвей), а затем вновь пополняется за счет энергии источника.
Для повышения крутизны резонансных характеристик, необходимой для более четкого разделения колебаний разных частот, в радиотехнике широко применяются двухконтурные резонансные цепи: два резонансных контура, настроенных каждый в отдельности на одну и ту же частоту, связываются индуктивно или электрически. В отличие от «одногорбой» резонансной кривой одиночного контура в связанных цепях получаются «двугорбые» кривые; например, ток в каждом контуре может иметь максимумы при двух частотах, расположенных ниже и выше резонансной частоты одиночного контура.
Частотные характеристики сопротивлений и проводимостей реактивных двухполюсников
Двухполюсником называется любая электрическая цепь или часть электрической цепи, имеющая два вывода. Ниже рассматриваются только линейные двухполюсники, т. е. такие, которые состоят из линейных элементов.
Различают двухполюсники активные и пассивные.
Активным называется двухполюсник, содержащий источники электрической энергии, которые не компенсируются взаимно внутри двухполюсника.
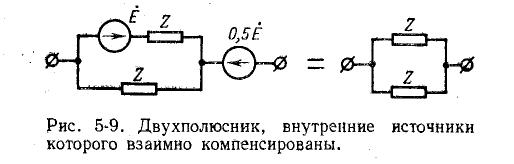
Пассивным называется двухполюсник, не содержащий источников электрической энергии; в случае линейного двухполюсника он может содержать источники электрической энергии, взаимно компенсирующиеся таким образом, что напряжение на его разомкнутых выводах равно нулю. Такой линейный двухполюсник относится к категории пассивных; его сопротивление, измеренное на выводах, не изменится, если источники электрической энергии внутри него заменить пассивными элементами — внутренними сопротивлениями источников э. д. с. или соответственно внутренними проводимостями источников тока. Пример двухполюсника, содержащего компенсированные источники, показан на рис. 5-9.
По числу элементов, входящих в двухполюсник, различают одноэлементный, двухэлементный и многоэлементный двухполюсники.
По характеру этих элементов двухполюсники делятся на реактивные, т. е. состоящие из индуктивностей и емкостей, и двухполюсники с потерями, содержащие активные сопротивления. Реактивные двухполюсники представляют собой идеализированные электрические системы, приближающиеся по своим свойствам к физически существующим цепям с малыми потерями.
Частотные характеристики сопротивлений или проводимостей двухполюсников, образующих электрическую цепь, предопределяют частотные и резонансные свойства цепи, т. е. зависимости амплитуд и фаз токов и напряжений от частоты.
Настоящий параграф посвящен изучению частотных характеристик пассивных реактивных двухполюсников.
Одноэлементные реактивные двухполюсники
Индуктивность и емкость представляют собой простейшие одноэлементные реактивные двухполюсники. Знак комплексного сопротивления и комплексной проводимости каждого из этих двухполюсников не зависит от частоты; этим они существенно отличаются от других, более сложных реактивных двухполюсников, содержащих неоднородные реактивные элементы, т. е. индуктивность и емкость в разных сочетаниях.
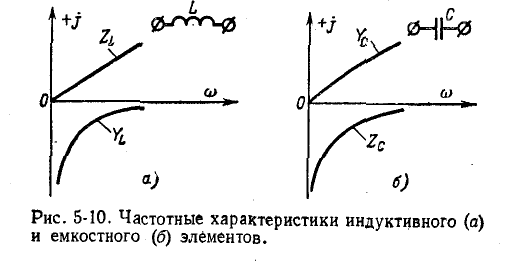
Комплексное сопротивление индуктивного элемента во всем спектре частот имеет положительный знак, а комплексная проводимость — отрицательный:
Комплексное сопротивление емкостного элемента во всем спектре частот имеет отрицательный знак, а комплексная проводимость — положительный:
В рассматриваемом случае реактивных двухполюсников комплексные сопротивления и проводимости являются мнимыми. Поэтому для сохранения знаков частотные ха-рактернстнкн сопротивлений и проводимостей удобно рисовать в прямоугольной системе координат, в которой вверх откладываются мнимые величины со знаком плюс, а вниз — со знаком минус.
Частотные характеристики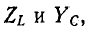
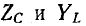
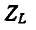
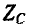
Следует заметить, что как сопротивления, так и проводимости рассматриваемых здесь одноэлементных реактивных двухполюсников возрастают (с учетом знака) по мере повышения частоты, т. е.
Это является общим свойством всех реактивных двухполюсников, а не только одноэлементных.
Двухполюсник, состоящий из последовательно или параллельно соединенных однородных элементов (индуктивностей или емкостей), относится к числу одноэлементных двухполюсников, так как последовательно или параллельно соединенные однородные элементы могут быть заменены одним эквивалентным реактивным элементом того же характера.
Двухэлементные реактивные двухполюсники
Двухэлементные двухполюсники, составленные из индуктивности и емкости, представляют собой простейшие резонансные цепи.
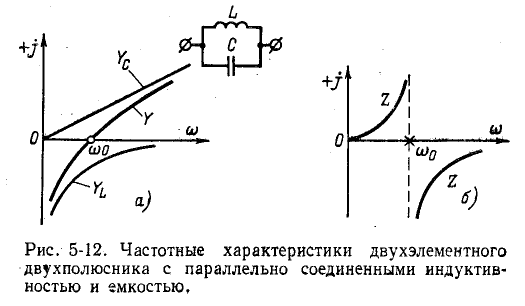
При последовательном соединении индуктивности и емкости алгебраически складываются комплексные сопротивления. На рис. 5-11, а жирной линией показана частотная характеристика двухполюсника, полученная в результате графического сложения кривых 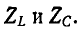
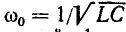
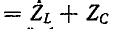
Частотная характеристика проводимости того же двухполюсника представляет собой функцию, обратную сопротивлению:
Кривая Y показана на рис. 5-11, б.
При резонансной частоте проводимость рассматриваемого двухполюсника обращается в бесконечность; эта точка носит название полюса функции Y и обозначается на чертеже крестиком
Частотные характеристики Z и Y, построенные таким образом1, соответствуют уравнениям:
и
или с учетом(5-2):
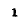
В области частот ниже резонансной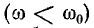
В области частот выше резонансной
При параллельном соединении индуктивности и емкости алгебраически складываются их комплексные проводимости. На рис. 5-12, а жирной линией показана частотная
характеристика двухполюсника, полученная в результате графического сложения
Частотная характеристика сопротивления того же двухполюсника представляет собой функцию, обратную проводимости: Z — 1/Y. Кривая Z показана на рис. 5-12, б.
Частота, при которой характеристика Y пересекает ось абсцисс (нуль функции У), а характеристика Z уходит в бесконечность (полюс функции Z), является резонансной частотой (резонанс токов).
Частотные характеристики, построенные на рис. 5-12, соответствуют уравнениям:
И
или с учетом (5-22)
В области частот ниже резонансной проводимость индуктивного элемента перекомпенсирует проводимость емкостного элемента и сопротивление двухполюсника получается, индуктивным. В области частот выше резонансной наблюдается обратное явление и сопротивление двухполюсника имеет емкостный характер.
Таким образом, в зависимости от частоты двухэлементный реактивный двухполюсник может иметь либо индуктивное, либо емкостное сопротивление. При этом, так же как и в случае одноэлементного реактивного двухполюсника, кривые Z и Y возрастают, т. е. производные от 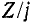
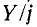
В отличие от сопротивлений одноэлементных двухполюсников, которые выражаются только через текущую частоту, сопротивления двухэлементных реактивных двухполюсников зависят также и от разности квадратов резонансной и текущей частот (формулы (5-21) и (5-22)1.
Как видно из выражений (5-21), для построения частотных характеристик двухполюсника, состоящего из последовательно соединенных элементов L и С, достаточно знать нуль функции Z или, что то же, полюс функции Y. Параметр L, входящий в (5-21), влияет только на выбор масштаба Z и Y по оси ординат.
Аналогично в соответствии с (5-22) для построения частотных характеристик двухполюсника, состоящего из параллельно соединенных элементов L и С, достаточно знать полюс Z или, что то же, нуль Y, причем параметр С влияет только на масштаб Z и Y.
Двухполюсники, имеющие одинаковые частотные характеристики Z или Y, эквивалентны.
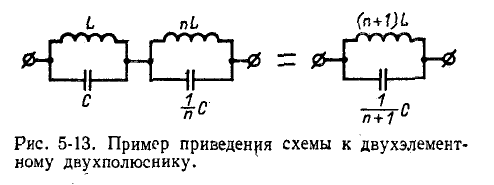
Многоэлементный реактивный двухполюсник
Многоэлементный реактивный двухполюсник может быть получен в результате различных сочетаний одноэлементных и двухэлементных двухполюсников. Пользуясь частотными характеристиками, приведенными выше, можно построить частотные характеристики для трех-, четырех- и много-элементных реактивных двухполюсников. При этом одно-
родные элементы (или группы элементов с одинаковыми резонансными частотами), соединенные параллельно или последовательно, должны быть сначала заменены одним элементом (или эквивалентной группой элементов, как это, например, показано на рис. 5-13).
Такие двухполюсники будем называть «приведенными».
Из свойства положительности производной 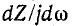
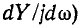
В общем случае, если при 
В противном случае порядок расположения резонансов обратный: первым наступает резонанс напряжений, вторым — резонанс токов и т. д.
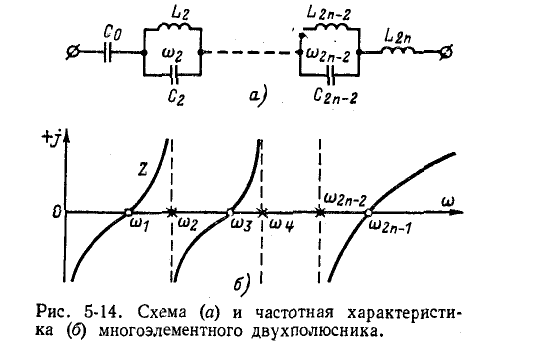
На рис. 5-14, а дана схема многоэлементного двухполюсника, а на рис. 5-14, б — соответствующая ему частотная характеристика сопротивления.
У реактивных двухполюсников сумма чисел полюсов и нулей (не считая точек 
Расположение нулей и полюсов, как указывалось выше, поочередное, а все ветви частотной характеристики с увеличением 
- Соединение звездой и треугольником в трехфазных цепях
- Принцип действия асинхронного и синхронного двигателей
- Метод симметричных составляющих
- Цепи периодического несинусоидального тока
- Расчет неразветвленной однородной магнитной цепи
- Энергия магнитного поля
- Синусоидальные Э.Д.С. и ток
- Электрические цепи с взаимной индуктивностью
Колебательный контур является типичным представителем резонансных колебательных систем, играющих важную роль в большинстве разделов физики — в механике это различного типа маятники и звуковые резонаторы (струны, мембраны, трубы, свистки, органы), в электродинамике — колебательные контуры, закрытые и открытые резонаторы с распределенными параметрами, в оптике — лазерные резонаторы, эталоны Фабри — Перо и т.д. Принципы описания всех колебательных систем настолько общи, что теория колебаний стала самостоятельным разделом физики. Поэтому изучение параметров, свойств и характеристик колебательного контура полезно рассматривать как общее введение в мир резонансных колебательных систем.
В теории колебаний выделяются два класса явлений — явления в линейных и нелинейных колебательных системах. Линейными называются такие системы, параметры которых не зависят от амплитуды колебаний. Например, для маятников это означает такие малые колебания, при которых упругость пружин и стержней не зависит от амплитуды колебания, а натяжение нити подвеса определяется только гравитационными силами. Для электрических колебательных контуров независимыми от амплитуды токов и напряжений должны оставаться такие величины, как индуктивность $L$, емкость $C$ и сопротивление $R$.
Резонансные системы имеют два важных свойства.
-
Свойство избирательно реагировать на внешние источники сигналов, выделяя только те из них, частоты которых совпадают с собственной частотой колебательной системы.
-
Свойство запасать энергию колебаний, возбужденных внешним источником, поддерживая колебания в течение определенного времени после выключения внешнего источника.
Колебательный контур характеризуется двумя основными параметрами: частотой собственных (резонансных) колебаний $omega _{0} $ и добротностью $Q$, характеризующей отношение мощности энергии собственного колебания к мощности потерь за период.

На рис. 18 приведены примеры «параллелей» электрических и механических колебательных систем. В электрических резонаторах происходит периодический переход электрической энергии, запасенной в конденсаторе $(W_Э =frac 12 CU^2),$ в магнитную энергию катушки индуктивности $(W_M =frac 12 LI^2)$ и обратно. В маятниках происходит аналогичный циклический переход энергии из потенциальной (поднятого груза или сжатой пружины) в кинетическую и обратно.
Свободные колебания происходят в замкнутой цепи без вынуждающей силы (рис. 19,а).
Согласно второму закону Кирхгофа для такой цепи можно написать:
$$
Rcdot I+U_{C} =-Lcdot frac{dI}{dt}.
$$
Выражая $U_{C} $ через заряд $q$, получим уравнение
$$
Rcdot I+Lcdot frac{dI}{dt} +frac{q}{C} =0 mbox{ (СИ). }
$$
Дифференцируя по времени и учитывая равенство $I=frac{dq}{dt} $, получаем
$$
Lfrac{d^{2} I}{dt^{2} } +Rfrac{dI}{dt} +frac{I}{C} =0 mbox{ (СИ). }
$$
Разделив на $L$ и вводя обозначения
$delta =frac{R}{2cdot L} $ и $omega _{0}^{2} =frac{1}{LC} $,
получим общее уравнение для свободных колебаний линейной резонансной системы:
$$
I»+2delta , I’+omega _{0}^{2} I=0,
$$
где параметр $delta $ называется затухание, а параметр $omega _{0} $ — собственная частота, или частота свободных колебаний. Оно решается подстановкой $I=Acdot e^{iomega , t} $, которая приводит к характеристическому уравнению
$$
-omega ^{2} +2iomega , delta +omega _{0}^{2} =0,
$$
с решением
$$
lambda , _{1,2} =i, delta pm sqrt{omega _{0}^{2} -delta ^{2} } .
$$
Общее решение имеет две составляющие
$$
I=Acdot e^{iomega _{1} , t} +Bcdot e^{iomega _{2} , t} .
$$
Константы $A$ и $B$ определяются начальными данными задачи, например, зарядом $q_{0} $ или напряжением на конденсаторе $U_{0} $. Характер начальных данных определяется конкретной физической системой.
Частный пример схемы для возбуждения свободных колебаний в колебательном контуре приведен на рис. 19,б. Конденсатор $C$ заряжается от батареи до напряжения $U_{0} $ (положение «а» переключателя), а затем переключается в точку «б». Свободные колебания будут представлять собой циклический переход энергии электрического поля (в конденсаторе) в энергию магнитного поля (в индуктивности) и обратно.
Подставив найденные значения $A$ и $B$, получим общее решение для свободных колебаний в контуре
$$
I=ifrac{U_{0} }{Lsqrt{omega _{0}^{2} -delta ^{2} } } e^{-delta , t} frac{e^{isqrt{omega _{0}^{2} -delta ^{2} } , t} -e^{-isqrt{omega _{0}^{2} -delta ^{2} } , t} }{2} .
$$
Если бы колебательный контур состоял только из идеальных (без потерь) реактивных элементов (индуктивности $L$ и емкости $C$), то переход энергии из электрической в магнитную и обратно совершался бы без потерь, а в контуре существовали бы незатухающие свободные колебания с собственной частотой $omega _{0} =2pi , f=sqrt{frac{1}{LC}}.$
Наличие в схеме активного элемента $R$ приводит к тому, что часть энергии за каждый период переходит в тепло и колебания затухают с некоторой постоянной времени $tau $. Роль частоты в уравнении теперь играет величина $omega _{p} =sqrt{omega _{0}^{2} -delta ^{2} } $, зависящая от отношения реактивной мощности к потерям на активном сопротивлении $R$. При этом вовсе не обязательно в схему должен быть включен отдельный резистор. В его качестве может выступать, например, омическое сопротивление провода, которым намотана катушка индуктивности, а также сопротивление утечки изоляторов конденсатора. Кроме того, часть энергии колебаний может излучаться контуром в окружающее пространство в виде электромагнитной волны. На этом основано действие так называемых связанных контуров: если вблизи данного колебательного контура расположен другой, то в нем «наводятся» (возникают) колебания за счет того, что часть энергии трансформируется из первого контура во второй. Передача энергии совершается переменным электромагнитным полем, возникающим вокруг первого контура.
Если затухание мало, т. е. $delta <omega _{0} $, то мы получаем уравнение слабо затухающих колебаний в виде
$$
I=-frac{U_{0} }{Lomega _{p} } e^{-delta , t} sin omega _{p} t=-I_{0} e^{-delta , t} sin omega _{p} t.
$$
При этом резонансная частота приближается к частоте собственных колебаний:
$$
omega _{p} =sqrt{omega _{0}^{2} -delta ^{2} } approx omega _{0} left(1-frac{1}{2} frac{delta ^{2} }{omega _{0}^{2} } right).
$$
Таким образом, при малом затухании резонансная частота практически совпадает с собственной, однако колебания при этом не являются гармоническими. Для гармонических колебаний должно соблюдаться условие $Ileft(tright)=Ileft(t+Tright)$, где $T$ — период колебания. В нашем случае $Ileft(tright)ne Ileft(t+Tright)$, и о периоде можно говорить лишь как о времени, через которое повторяются нули функции (рис. 20). Именно в этом смысле мы будем ниже использовать термин «период колебаний».

Введем понятия добротности $Q$ и логарифмического декремента затухания $gamma $ контура. Из отношение амплитуд $n$–того и $(n + k)$–го колебаний равно
$I_{n} I_{n+k}^{-1} = e^{kdelta T}$, где $T=2, pi omega ^{-1} $ — период колебания («повторения нулей»). Логарифмическим декрементом затухания $gamma $ называется величина
$$
gamma =delta , T=frac{1}{k} ln frac{I_{n} }{I_{n+k} } =ln frac{I_{n} }{I_{n+1} } .
$$
Из уравнения для тока видно, что величина $delta $ обратно пропорциональна времени, за которое амплитуда колебаний уменьшается в $e$ раз. Из последнего уравнения следует, что декремент затухания $gamma $ показывает уменьшение амплитуды за период колебания:
$$
gamma =delta , T=frac{2; pi , delta }{omega } .
$$
С логарифмическим коэффициентом затухания однозначно связан другой, более распространенный параметр, характеризующий колебательную систему, добротность $Q$.
Добротность контура $Q$ определяется соотношением
$$
Q=frac{omega _{0} L}{R} =frac{1}{omega _{0} CR} =frac{rho }{R},
$$
где $rho =sqrt{frac LC} $ (СИ).
Физический смысл добротности заключается в отношении запасенной в контуре энергии к энергии потерь за период колебания
$$
Q=omega cdot frac{W_0}{Delta W},
$$
откуда можно найти связь добротности с другими параметрами контура
$$
Q=frac{pi }{gamma } =frac{pi }{delta , T} =frac{omega }{2, delta } =omega frac{L}{R} mbox{ (СИ).}
$$
Экспериментально добротность определяется по резонансной кривой как отношение резонансной частоты $omega _{p} $ к полосе частот $2cdot Delta omega $, определяемой на уровне $U_{1,2} =pm frac{U_p}{sqrt{2}}$:
$$
Q=frac{omega _{з}}{2cdot Delta omega } =frac{f_{з}}{2cdot Delta f} ,
$$
где $U_{p} $ — амплитуда колебания на резонансной частоте контура. Величина $rho =sqrt{frac LC}$ называется характеристическим (волновым) сопротивлением контура.
При большом затухании, т.е. при $delta >omega _{0} $, величина $omega _{0}^{2} -delta ^{2} $ отрицательна, корень из нее мнимый. Такой случай называется апериодическим процессом. Общее решение, аналогичное, полученному ранее, будет иметь вид
$$
I=-frac{U_{0} }{Lsqrt{(delta ^{2} -omega _{0}^{2} )} } e^{-delta , , t} mbox{sh}sqrt{(delta ^{2} -omega _{0}^{2} )} , t.
$$
График этой функции приведен на рис. 21.
Критическим условием, при котором затухающие колебания переходят в апериодический процесс, является условие $delta =omega _{0} $. В этом случае решение общего уравнения имеет вид
$$
I=-frac{U_{0} }{omega L} (omega t)e^{-delta , t} , =-frac{U_{0} }{L} t, e^{-delta , t} .
$$
Остается добавить, что аналогичные параметры могут быть введены для любой резонансной колебательной системы независимо от ее физической природы (механические, термодинамические, электромагнитные, оптические, аэро– и гидродинамические системы).
Колебательный контур, рассмотренный в предыдущем разделе, представлял собой замкнутую электрическую цепь, в которой совершаются свободные колебания.
В случае вынужденных колебаний мы должны подводить к контуру электрическую энергию от внешнего источника (генератора). Есть много способов для подключения источника внешней энергии к контуру, которые сводятся к той или иной комбинации двух основных: в разрыв цепи контура (рис. 22, а) или параллельно емкостной и индуктивной ветвям контура (рис. 22,б).
В зависимости от способа включения различают соответственно последовательный (рис. 22,а) и параллельный (рис. 22,б) колебательные контуры. Они предъявляют разные требования к согласованию с генератором и нагрузкой. Поэтому нужно отличать собственные параметры контура от параметров нагруженного контура, получаемые с учетом влияния генератора и «нагрузки» (входного сопротивления той цепи, в которую включен контур). В параллельном контуре (рис. 22,б) возникает резонанс токов. Для его поддержания в качестве вынуждающей силы необходимо применение генератора стабильного тока. В последовательном контуре (рис. 22,а) имеет место резонанс напряжений, и для его поддержания должен применяться внешний генератор стабильного напряжения.
Закон Кирхгофа, позволяющий исследовать процессы в контуре (рис. 22,а) в зависимости от частоты, записывается в виде
$$
U=U_{R} +U_{L} +U_{C} =IR+iI(omega L-frac{1}{omega C} )=Icdot Z.
$$
Контур представляет для генератора некоторое комплексное сопротивление
$$
Z=R_L +icdot (omega L-frac{1}{omega C} ),
$$
$$
left|Zright| = sqrt{R_L^2 +(omega L-frac{1}{omega C})^2}, mbox{tg}varphi =frac{omega L-frac{1}{omega C} }{R_L}
$$
где $left|Zright|$ — модуль комплексного сопротивления; $R_{L}$ — омическое сопротивление катушки индуктивности; $varphi $ — сдвиг фазы между активным и реактивным сопротивлениями, равный сдвигу фазы между током $I$ в цепи и входным напряжением $U$.
Из последнего выражения видно, что сопротивление цепи будет минимально и равно активному сопротивлению $R_{L} $ на некоторой частоте $omega _{0} $, определяемой условием
$$
omega _0 L=frac{1}{omega _0 C} , mbox{ где } omega _{0} =frac{1}{sqrt{LC}} mbox{ (СИ).}
$$
Таким образом, на резонансной частоте сопротивление контура минимально, чисто активно, а ток в цепи совпадает по фазе с входным напряжением (напряжением генератора). Фактически это и есть определение резонанса в последовательном колебательном контуре.
Для практических целей представляет интерес исследовать поведение напряжений на реактивных элементах контура в зависимости от частоты генератора и определить его добротность $Q$.
Поскольку фазы $U_{L} $ и $U_{C} $ независимо от частоты всегда сдвинуты относительно тока $I$ на $+$ и $-90^{circ}$ соответственно, то достаточно исследовать зависимость от частоты их модулей. Это можно сделать исходя из уравнений
$$
U_{R} =IR, U_{L} =Iomega L, U_{C} =frac{I}{omega C}, I=frac{U}{Z} .
$$
Для примера раскроем уравнения для $I$ и $U_{L} $. Используя введенное для свободных колебаний понятие добротности $Q=left(omega _{0} RCright)^{-1}$, получим следующее выражение для тока в последовательном контуре:
$$
I=frac{U}{sqrt{R^{2} +(omega L-frac{1}{omega C} )^{2} } } =frac{U}{R} frac{1}{sqrt{1+Q^{2} (frac{omega }{omega _{0} } -frac{omega _{0} }{omega } )^{2} } } .
$$
Тогда напряжение на индуктивности будет равно
$$
U_{L} =omega LI=Ufrac{Qfrac{omega }{omega _{0} } }{sqrt{1+Q^{2} (frac{omega }{omega _{0} } -frac{omega _{0} }{omega } )^{2} } } .
$$
Аналогичное уравнение можно получить для напряжения на $C$. При $omega =omega _{0} $ напряжения на $L$ и $C$ будут равны $U_{L0} =U_{C0} =Qcdot U$, т.е. в $Q$ раз больше напряжения вынуждающей эдс.
На самом деле максимумы напряжения на элементах $L$ и $C$ несколько выше и смещены от резонансной частоты и выражаются следующими соотношениями:
$$
omega _{Lmax } =omega _{0} sqrt{frac{2}{2-frac{R^{2} C}{L} } } =omega _{0} sqrt{frac{2}{2-left(frac{1}{Q} right)^{2} } } , omega _{Cmax } =frac{omega _{0}^{2} }{omega _{L} } .
$$
При добротности контура $Q ge 10$ сдвиг частот максимумов $U_{L} $ и $U_{C} $ относительно резонансной частоты $omega _{0} $ не превышает 1% и экспериментально резонансную частоту и добротность можно определять по резонансной кривой любого из напряжений $U_{L} $ и $U_{C} $. Напряжение на реактивных элементах $U_{L} $ и $U_{C} $ при $omega =omega _{0} $ в $Q$ раз больше, чем входное напряжение $U$, поэтому резонанс в последовательном контуре называется резонансом напряжений.
Важно отметить, что для нашего анализа существенно, что само входное напряжение $U$ от частоты не зависит. В противном случае все параметры зависели бы не только от самого контура, но и от параметров источника сигнала. Как было показано в предыдущем параграфе, для этого выходное сопротивление генератора должно быть много меньше $R$.
Схема подключения параллельного контура представлена на рис. 21,б. Из–за комплексного характера нагрузки ток генератора является комплексной величиной. Поэтому модуль тока $I$ может оказаться меньше не только суммы модулей токов индуктивной и емкостной ветвей контура, но и каждого из них в отдельности. Именно это и происходит при резонансе в параллельном контуре: токи в индуктивной и емкостной ветвях контура в $Q$ раз больше, чем ток, потребляемый от генератора тока. Поэтому резонанс в параллельном контуре называется резонансом токов.
Комплексное сопротивление параллельного контура равно
$$
Z=frac{Z_{1} Z_{2} }{Z_{1} +Z_{2} } =
frac{(R_{L} +iomega L)(iomega C)^{-1}}{R_{L} +i(omega L-(omega C)^{-1} )} approx
frac{LC^{-1}}{R_{L} +i(omega L-(omega C)^{-1})} .
$$
Мы пренебрегли величиной $R_{L} $ в числителе, поскольку она в $Q$ раз меньше индуктивного сопротивления, но этого нельзя делать в знаменателе, поскольку при резонансе величина в скобках стремится к нулю.
Условие резонанса для параллельного контура то же, что и для последовательного — равенство реактивных сопротивлений ветвей с $L$ и $C$:
$$
omega _{0} L=frac{1}{omega _{0} C}, mbox{ где } omega _{0} =frac{1}{sqrt{LC} } mbox{ (СИ). }
$$
Таким образом, при резонансе сопротивление контура становится чисто активным и равным
$$
R_{э} =frac{L}{ C R_{L} } =frac{rho ^{2} }{R_{L} } ,
$$
где — $rho =sqrt{frac LC} $ волновое сопротивление контура.
Сопротивление $R_{э} $ отдельного физического эквивалента в контуре не имеет, а является комбинацией волнового сопротивления $rho $ и сопротивления потерь $R_{L} $. Поэтому оно не составляет отдельной ветви параллельного контура и не ответвляет в себя ток. Следовательно, «переносить» его куда–либо или к чему–нибудь «подсоединять» (например, к внутреннему сопротивлению источника тока) бессмысленно. На схеме это просто условное обозначение того факта, что на резонансной частоте параллельный колебательный контур представляет для внешнего генератора некоторое чисто активное сопротивление величиной $R_{э} $, а в формулах символическая запись определенной комбинации $rho $ и $R_{L} $, даваемой последней формулой.
Добротность параллельного контура
$$
Q=frac{omega _{0} L}{R_{L} } =frac{1}{R_{L} omega _{0} C} =frac{R_{э} }{rho } =R_{э} sqrt{frac{C}{L} } .
$$
Собственные параметры параллельного контура, т.е. резонансная частота $omega _{0} $ и добротность $Q$ будут такими же, как и в последовательном контуре при тех же $C$, $L$ и $R_{L}.$