Figure 1 Hard wheel rolling on and deforming a soft surface, resulting in the reaction force R from the surface having a component that opposes the motion. (W is some vertical load on the axle, F is some towing force applied to the axle, r is the wheel radius, and both friction with the ground and friction at the axle are assumed to be negligible and so are not shown. The wheel is rolling to the left at constant speed.) Note that R is the resultant force from non-uniform pressure at the wheel-roadbed contact surface. This pressure is greater towards the front of the wheel due to hysteresis.
Rolling resistance, sometimes called rolling friction or rolling drag, is the force resisting the motion when a body (such as a ball, tire, or wheel) rolls on a surface. It is mainly caused by non-elastic effects; that is, not all the energy needed for deformation (or movement) of the wheel, roadbed, etc., is recovered when the pressure is removed. Two forms of this are hysteresis losses (see below), and permanent (plastic) deformation of the object or the surface (e.g. soil). Note that the slippage between the wheel and the surface also results in energy dissipation. Although some researchers have included this term in rolling resistance, some suggest that this dissipation term should be treated separately from rolling resistance because it is due to the applied torque to the wheel and the resultant slip between the wheel and ground, which is called slip loss or slip resistance.[1] In addition, only the so-called slip resistance involves friction, therefore the name «rolling friction» is to an extent a misnomer.
Analogous with sliding friction, rolling resistance is often expressed as a coefficient times the normal force. This coefficient of rolling resistance is generally much smaller than the coefficient of sliding friction.[2]
Any coasting wheeled vehicle will gradually slow down due to rolling resistance including that of the bearings, but a train car with steel wheels running on steel rails will roll farther than a bus of the same mass with rubber tires running on tarmac/asphalt. Factors that contribute to rolling resistance are the (amount of) deformation of the wheels, the deformation of the roadbed surface, and movement below the surface. Additional contributing factors include wheel diameter,[3] load on wheel, surface adhesion, sliding, and relative micro-sliding between the surfaces of contact. The losses due to hysteresis also depend strongly on the material properties of the wheel or tire and the surface. For example, a rubber tire will have higher rolling resistance on a paved road than a steel railroad wheel on a steel rail. Also, sand on the ground will give more rolling resistance than concrete. Sole rolling resistance factor is not dependent on speed.
Primary cause[edit]
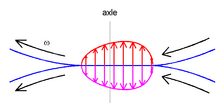
Asymmetrical pressure distribution between rolling cylinders due to viscoelastic material behavior (rolling to the right).[4]
The primary cause of pneumatic tire rolling resistance is hysteresis:[5]
A characteristic of a deformable material such that the energy of deformation is greater than the energy of recovery. The rubber compound in a tire exhibits hysteresis. As the tire rotates under the weight of the vehicle, it experiences repeated cycles of deformation and recovery, and it dissipates the hysteresis energy loss as heat. Hysteresis is the main cause of energy loss associated with rolling resistance and is attributed to the viscoelastic characteristics of the rubber.
- — National Academy of Sciences[6]
This main principle is illustrated in the figure of the rolling cylinders. If two equal cylinders are pressed together then the contact surface is flat. In the absence of surface friction, contact stresses are normal (i.e. perpendicular) to the contact surface. Consider a particle that enters the contact area at the right side, travels through the contact patch and leaves at the left side. Initially its vertical deformation is increasing, which is resisted by the hysteresis effect. Therefore, an additional pressure is generated to avoid interpenetration of the two surfaces. Later its vertical deformation is decreasing. This is again resisted by the hysteresis effect. In this case this decreases the pressure that is needed to keep the two bodies separate.
The resulting pressure distribution is asymmetrical and is shifted to the right. The line of action of the (aggregate) vertical force no longer passes through the centers of the cylinders. This means that a moment occurs that tends to retard the rolling motion.
Materials that have a large hysteresis effect, such as rubber, which bounce back slowly, exhibit more rolling resistance than materials with a small hysteresis effect that bounce back more quickly and more completely, such as steel or silica. Low rolling resistance tires typically incorporate silica in place of carbon black in their tread compounds to reduce low-frequency hysteresis without compromising traction.[7] Note that railroads also have hysteresis in the roadbed structure.[8]
Definitions[edit]
In the broad sense, specific «rolling resistance» (for vehicles) is the force per unit vehicle weight required to move the vehicle on level ground at a constant slow speed where aerodynamic drag (air resistance) is insignificant and also where there are no traction (motor) forces or brakes applied. In other words, the vehicle would be coasting if it were not for the force to maintain constant speed.[9] This broad sense includes wheel bearing resistance, the energy dissipated by vibration and oscillation of both the roadbed and the vehicle, and sliding of the wheel on the roadbed surface (pavement or a rail).
But there is an even broader sense that would include energy wasted by wheel slippage due to the torque applied from the engine. This includes the increased power required due to the increased velocity of the wheels where the tangential velocity of the driving wheel(s) becomes greater than the vehicle speed due to slippage. Since power is equal to force times velocity and the wheel velocity has increased, the power required has increased accordingly.
The pure «rolling resistance» for a train is that which happens due to deformation and possible minor sliding at the wheel-road contact.[10] For a rubber tire, an analogous energy loss happens over the entire tire, but it is still called «rolling resistance». In the broad sense, «rolling resistance» includes wheel bearing resistance, energy loss by shaking both the roadbed (and the earth underneath) and the vehicle itself, and by sliding of the wheel, road/rail contact. Railroad textbooks seem to cover all these resistance forces but do not call their sum «rolling resistance» (broad sense) as is done in this article. They just sum up all the resistance forces (including aerodynamic drag) and call the sum basic train resistance (or the like).[11]
Since railroad rolling resistance in the broad sense may be a few times larger than just the pure rolling resistance[12] reported values may be in serious conflict since they may be based on different definitions of «rolling resistance». The train’s engines must, of course, provide the energy to overcome this broad-sense rolling resistance.
For tires, rolling resistance is defined as the energy consumed by a tire per unit distance covered.[13] It is also called rolling friction or rolling drag. It is one of the forces that act to oppose the motion of a driver. The main reason for this is that when the tires are in motion and touch the surface, the surface changes shape and causes deformation of the tire.[14]
For highway motor vehicles, there is obviously some energy dissipated in shaking the roadway (and the earth beneath it), the shaking of the vehicle itself, and the sliding of the tires. But, other than the additional power required due to torque and wheel bearing friction, non-pure rolling resistance doesn’t seem to have been investigated, possibly because the «pure» rolling resistance of a rubber tire is several times higher than the neglected resistances.[15]
Rolling resistance coefficient[edit]
The «rolling resistance coefficient» is defined by the following equation:[6]
where





of load or Newtons/kilo-Newton, etc. For the US railroads, lb/ton has been traditionally used; this is just 


The above shows resistance proportional to 


Measurement[edit]
There are at least two popular models for calculating rolling resistance.
- «Rolling resistance coefficient (RRC). The value of the rolling resistance force divided by the wheel load. The Society of Automotive Engineers (SAE) has developed test practices to measure the RRC of tires. These tests (SAE J1269 and SAE J2452) are usually performed[citation needed] on new tires. When measured by using these standard test practices, most new passenger tires have reported RRCs ranging from 0.007 to 0.014.»[6] In the case of bicycle tires, values of 0.0025 to 0.005 are achieved.[18] These coefficients are measured on rollers, with power meters on road surfaces, or with coast-down tests. In the latter two cases, the effect of air resistance must be subtracted or the tests performed at very low speeds.
- The coefficient of rolling resistance b, which has the dimension of length, is approximately (due to the small-angle approximation of
) equal to the value of the rolling resistance force times the radius of the wheel divided by the wheel load.[3]
- ISO 18164:2005 is used to test rolling resistance in Europe.
The results of these tests can be hard for the general public to obtain as manufacturers prefer to publicize «comfort» and «performance».
Physical formulae[edit]
The coefficient of rolling resistance for a slow rigid wheel on a perfectly elastic surface, not adjusted for velocity, can be calculated by [19][citation needed]
where
The empirical formula for 
where
As an alternative to using 

where
The above equation, where resistance is inversely proportional to radius 







Rolling resistance coefficient examples[edit]
Table of rolling resistance coefficient examples: [4]
| Crr | b | Description |
|---|---|---|
| 0.0003 to 0.0004[21] | «Pure rolling resistance» Railroad steel wheel on steel rail | |
| 0.0010 to 0.0015[22] | 0.1 mm[3] | Hardened steel ball bearings on steel |
| 0.0010 to 0.0024[23][24] | 0.5 mm[3] | Railroad steel wheel on steel rail. Passenger rail car about 0.0020[25] |
| 0.0019 to 0.0065[26] | Mine car cast iron wheels on steel rail | |
| 0.0022 to 0.0050[27] | Production bicycle tires at 120 psi (8.3 bar) and 50 km/h (31 mph), measured on rollers | |
| 0.0025[28] | Special Michelin solar car/eco-marathon tires | |
| 0.0050 | Dirty tram rails (standard) with straights and curves[citation needed] | |
| 0.0045 to 0.0080[29] | Large truck (Semi) tires | |
| 0.0055[28] | Typical BMX bicycle tires used for solar cars | |
| 0.0062 to 0.0150[30] | Car tire measurements | |
| 0.0100 to 0.0150[31] | Ordinary car tires on concrete | |
| 0.0385 to 0.0730[32] | Stage coach (19th century) on dirt road. Soft snow on road for worst case. | |
| 0.3000[31] | Ordinary car tires on sand |
For example, in earth gravity, a car of 1000 kg on asphalt will need a force of around 100 newtons for rolling (1000 kg × 9.81 m/s2 × 0.01 = 98.1 N).
Dependence on diameter[edit]
Stagecoaches and railroads[edit]
According to Dupuit (1837), rolling resistance (of wheeled carriages with wooden wheels with iron tires) is approximately inversely proportional to the square root of wheel diameter.[33] This rule has been experimentally verified for cast iron wheels (8″ — 24″ diameter) on steel rail[34] and for 19th century carriage wheels.[32] But there are other tests on carriage wheels that do not agree.[32] Theory of a cylinder rolling on an elastic roadway also gives this same rule[35] These contradict earlier (1785) tests by Coulomb of rolling wooden cylinders where Coulomb reported that rolling resistance was inversely proportional to the diameter of the wheel (known as «Coulomb’s law»).[36] This disputed (or wrongly applied)
-«Coulomb’s law» is still found in handbooks, however.
Pneumatic tires[edit]
For pneumatic tires on hard pavement, it is reported that the effect of diameter on rolling resistance is negligible (within a practical range of diameters).[37][38]
Dependence on applied torque[edit]
The driving torque 

where
It is noteworthy that 
All wheels[edit]
«Applied torque» may either be driving torque applied by a motor (often through a transmission) or a braking torque applied by brakes (including regenerative braking). Such torques results in energy dissipation (above that due to the basic rolling resistance of a freely rolling, i.e. except slip resistance). This additional loss is in part due to the fact that there is some slipping of the wheel, and for pneumatic tires, there is more flexing of the sidewalls due to the torque. Slip is defined such that a 2% slip means that the circumferential speed of the driving wheel exceeds the speed of the vehicle by 2%.
A small percentage slip can result in a slip resistance which is much larger than the basic rolling resistance. For example, for pneumatic tires, a 5% slip can translate into a 200% increase in rolling resistance.[46] This is partly because the tractive force applied during this slip is many times greater than the rolling resistance force and thus much more power per unit velocity is being applied (recall power = force x velocity so that power per unit of velocity is just force). So just a small percentage increase in circumferential velocity due to slip can translate into a loss of traction power which may even exceed the power loss due to basic (ordinary) rolling resistance. For railroads, this effect may be even more pronounced due to the low rolling resistance of steel wheels.
It is shown that for a passenger car, when the tractive force is about 40% of the maximum traction, the slip resistance is almost equal to the basic rolling resistance (hysteresis loss). But in case of a tractive force equal to 70% of the maximum traction, slip resistance becomes 10 times larger than the basic rolling resistance.[1]
Railroad steel wheels[edit]
In order to apply any traction to the wheels, some slippage of the wheel is required.[47] For trains climbing up a grade, this slip is normally 1.5% to 2.5%.
Slip (also known as creep) is normally roughly directly proportional to tractive effort. An exception is if the tractive effort is so high that the wheel is close to substantial slipping (more than just a few percent as discussed above), then slip rapidly increases with tractive effort and is no longer linear. With a little higher applied tractive effort the wheel spins out of control and the adhesion drops resulting in the wheel spinning even faster. This is the type of slipping that is observable by eye—the slip of say 2% for traction is only observed by instruments. Such rapid slip may result in excessive wear or damage.
Pneumatic tires[edit]
Rolling resistance greatly increases with applied torque. At high torques, which apply a tangential force to the road of about half the weight of the vehicle, the rolling resistance may triple (a 200% increase).[46] This is in part due to a slip of about 5%. The rolling resistance increase with applied torque is not linear, but increases at a faster rate as the torque becomes higher.
Dependence on wheel load[edit]
Railroad steel wheels[edit]
The rolling resistance coefficient, Crr, significantly decreases as the weight of the rail car per wheel increases.[48] For example, an empty freight car had about twice the Crr as a loaded car (Crr=0.002 vs. Crr=0.001). This same «economy of scale» shows up in testing of mine rail cars.[49] The theoretical Crr for a rigid wheel rolling on an elastic roadbed shows Crr inversely proportional to the square root of the load.[35]
If Crr is itself dependent on wheel load per an inverse square-root rule, then for an increase in load of 2% only a 1% increase in rolling resistance occurs.[50]
Pneumatic tires[edit]
For pneumatic tires, the direction of change in Crr (rolling resistance coefficient) depends on whether or not tire inflation is increased with increasing load.[51] It is reported that, if inflation pressure is increased with load according to an (undefined) «schedule», then a 20% increase in load decreases Crr by 3%. But, if the inflation pressure is not changed, then a 20% increase in load results in a 4% increase in Crr. Of course, this will increase the rolling resistance by 20% due to the increase in load plus 1.2 x 4% due to the increase in Crr resulting in a 24.8% increase in rolling resistance.[52]
Dependence on curvature of roadway[edit]
General[edit]
When a vehicle (motor vehicle or railroad train) goes around a curve, rolling resistance usually increases. If the curve is not banked so as to exactly counter the centrifugal force with an equal and opposing centripetal force due to the banking, then there will be a net unbalanced sideways force on the vehicle.
This will result in increased rolling resistance. Banking is also known as «superelevation» or «cant» (not to be confused with rail cant of a rail). For railroads, this is called curve resistance but for roads it has (at least once) been called rolling resistance due to cornering.
Sound[edit]
Rolling friction generates sound (vibrational) energy, as mechanical energy is converted to this form of energy due to the friction. One of the most common examples of rolling friction is the movement of motor vehicle tires on a roadway, a process which generates sound as a by-product.[53] The sound generated by automobile and truck tires as they roll (especially noticeable at highway speeds) is mostly due to the percussion of the tire treads, and compression (and subsequent decompression) of air temporarily captured within the treads.[54]
Factors that contribute in tires[edit]
Several factors affect the magnitude of rolling resistance a tire generates:
- As mentioned in the introduction: wheel radius, forward speed, surface adhesion, and relative micro-sliding.
- Material — different fillers and polymers in tire composition can improve traction while reducing hysteresis. The replacement of some carbon black with higher-priced silica–silane is one common way of reducing rolling resistance.[6] The use of exotic materials including nano-clay has been shown to reduce rolling resistance in high performance rubber tires.[55] Solvents may also be used to swell solid tires, decreasing the rolling resistance.[56]
- Dimensions — rolling resistance in tires is related to the flex of sidewalls and the contact area of the tire[57] For example, at the same pressure, wider bicycle tires flex less in the sidewalls as they roll and thus have lower rolling resistance (although higher air resistance).[57]
- Extent of inflation — Lower pressure in tires results in more flexing of the sidewalls and higher rolling resistance.[57] This energy conversion in the sidewalls increases resistance and can also lead to overheating and may have played a part in the infamous Ford Explorer rollover accidents.
- Over inflating tires (such a bicycle tires) may not lower the overall rolling resistance as the tire may skip and hop over the road surface. Traction is sacrificed, and overall rolling friction may not be reduced as the wheel rotational speed changes and slippage increases.[citation needed]
- Sidewall deflection is not a direct measurement of rolling friction. A high quality tire with a high quality (and supple) casing will allow for more flex per energy loss than a cheap tire with a stiff sidewall.[citation needed] Again, on a bicycle, a quality tire with a supple casing will still roll easier than a cheap tire with a stiff casing. Similarly, as noted by Goodyear truck tires, a tire with a «fuel saving» casing will benefit the fuel economy through many tread lives (i.e. retreading), while a tire with a «fuel saving» tread design will only benefit until the tread wears down.
- In tires, tread thickness and shape has much to do with rolling resistance. The thicker and more contoured the tread, the higher the rolling resistance[57] Thus, the «fastest» bicycle tires have very little tread and heavy duty trucks get the best fuel economy as the tire tread wears out.
- Diameter effects seem to be negligible, provided the pavement is hard and the range of diameters is limited. See dependence on diameter.
- Virtually all world speed records have been set on relatively narrow wheels,[citation needed] probably because of their aerodynamic advantage at high speed, which is much less important at normal speeds.
- Temperature: with both solid and pneumatic tires, rolling resistance has been found to decrease as temperature increases (within a range of temperatures: i.e. there is an upper limit to this effect)[58][59] For a rise in temperature from 30 °C to 70 °C the rolling resistance decreased by 20-25%.[60] Racers heat their tires before racing, but this is primarily used to increase tire friction rather than to decrease rolling resistance.
Railroads: Components of rolling resistance[edit]
In a broad sense rolling resistance can be defined as the sum of components[61]):
- Wheel bearing torque losses.
- Pure rolling resistance.
- Sliding of the wheel on the rail.
- Loss of energy to the roadbed (and earth).
- Loss of energy to oscillation of railway rolling stock.
Wheel bearing torque losses can be measured as a rolling resistance at the wheel rim, Crr. Railroads normally use roller bearings which are either cylindrical (Russia)[62] or tapered (United States).[63] The specific rolling resistance in bearings varies with both wheel loading and speed.[64] Wheel bearing rolling resistance is lowest with high axle loads and intermediate speeds of 60–80 km/h with a Crr of 0.00013 (axle load of 21 tonnes). For empty freight cars with axle loads of 5.5 tonnes, Crr goes up to 0.00020 at 60 km/h but at a low speed of 20 km/h it increases to 0.00024 and at a high speed (for freight trains) of 120 km/h it is 0.00028. The Crr obtained above is added to the Crr of the other components to obtain the total Crr for the wheels.
Comparing rolling resistance of highway vehicles and trains[edit]
The rolling resistance of steel wheels on steel rail of a train is far less than that of the rubber tires wheels of an automobile or truck. The weight of trains varies greatly; in some cases they may be much heavier per passenger or per net ton of freight than an automobile or truck, but in other cases they may be much lighter.
As an example of a very heavy passenger train, in 1975, Amtrak passenger trains weighed a little over 7 tonnes per passenger,[65] which is much heavier than an average of a little over one ton per passenger for an automobile. This means that for an Amtrak passenger train in 1975, much of the energy savings of the lower rolling resistance was lost to its greater weight.
An example of a very light high-speed passenger train is the N700 Series Shinkansen, which weighs 715 tonnes and carries 1323 passengers, resulting in a per-passenger weight of about half a tonne. This lighter weight per passenger, combined with the lower rolling resistance of steel wheels on steel rail means that an N700 Shinkansen is much more energy efficient than a typical automobile.
In the case of freight, CSX ran an advertisement campaign in 2013 claiming that their freight trains move «a ton of freight 436 miles on a gallon of fuel», whereas some sources claim trucks move a ton of freight about 130 miles per gallon of fuel, indicating trains are more efficient overall.
See also[edit]
- Coefficient of friction
- Low-rolling resistance tires
- Maglev (Magnetic Levitation, the elimination of rolling and thus rolling resistance)
- Rolling element bearing
References[edit]
- ^ a b «SAE MOBILUS». saemobilus.sae.org. doi:10.4271/06-11-02-0014. Retrieved 2021-04-19.
- ^ Peck, William Guy (1859). Elements of Mechanics: For the Use of Colleges, Academies, and High Schools. A.S. Barnes & Burr: New York. p. 135. Retrieved 2007-10-09.
rolling friction less than sliding friction.
- ^ a b c d e Hibbeler, R.C. (2007). Engineering Mechanics: Statics & Dynamics (Eleventh ed.). Pearson, Prentice Hall. pp. 441–442. ISBN 9780132038096.
- ^ «User guide for CONTACT, Rolling and sliding contact with friction. Technical report TR09-03 version v16.1. VORtech, 2016» (PDF). Retrieved 2017-07-11.
- ^ A handbook for the rolling resistance of pneumatic tires Clark, Samuel Kelly; Dodge, Richard N. 1979
- ^ a b c d «Tires and Passenger Vehicle Fuel Economy: Informing Consumers, Improving Performance — Special Report 286. National Academy of Sciences, Transportation Research Board, 2006» (PDF). Retrieved 2007-08-11.
- ^ Tyres-Online: The Benefits of Silica in Tyre Design Archived 2013-02-04 at the Wayback Machine
- ^ Астахов, p.85
- ^ An example of such usage for railroads is here.
- ^ Деев, p. 79. Hay, p. 68
- ^ Астахов, Chapt. IV, p. 73+; Деев, Sect. 5.2 p. 78+; Hay, Chapt. 6 «Train Resistance» p. 67+
- ^ Астахов, Fig. 4.14, p. 107
- ^ Andersen Lasse G.; Larsen Jesper K.; Fraser Elsje S.; Schmidt Bjarne; Dyre Jeppe C. (2015). «Rolling Resistance Measurement and Model Development». Journal of Transportation Engineering. 141 (2): 04014075. doi:10.1061/(ASCE)TE.1943-5436.0000673.
- ^ «Rolling Resistance and Fuel Saving» (PDF). Archived from the original (PDF) on 2016-04-08.
- ^ If one were to assume that the resistance coefficients (Crr) for motor vehicles were the same as for trains, then for trains the neglected resistances taken together have a Crr of about 0.0004 (see Астахов, Fig. 4.14, p.107 at 20km/hr and assume a total Crr =0.0010 based on Fig. 3.8, p.50 (plain bearings) and adjust for roller bearings based on a delta Crr of 0.00035 as read from Figs. 4.2 and 4.4 on pp. 74, 76). Compare this Crr of 0.0004 to motor vehicle tire Crr’s of at least 10 times higher per «Rolling resistance coefficient examples» in this article
- ^ kgf/tonne is used by Астахов throughout his book
- ^ Деев uses N/T notation. See pp. 78-84.
- ^ Willett, Kraig. «Roller Data». www.biketechreview.com. Retrieved 2017-08-05.
- ^ Guiggiani, Massimo (5 May 2018). The Science of Vehicle Dynamics. Springer Cham. p. 22. ISBN 978-3-319-73220-6.
- ^ Hersey, equation (2), p. 83
- ^ Астахов, p. 81.
- ^ «Coefficients of Friction in Bearing». Coefficients of Friction. Retrieved 7 February 2012.
- ^ Hay, Fig. 6-2 p.72(worst case shown of 0.0036 not used since it is likely erroneous)
- ^ Астахов, Figs. 3.8, 3.9, 3.11, pp. 50-55; Figs. 2.3, 2.4 pp. 35-36. (Worst case is 0.0024 for an axle load of 5.95 tonnes with obsolete plain (friction —not roller) bearings
- ^ Астахов, Fig. 2.1, p.22
- ^ Hersey, Table 6, p.267
- ^ «Roller Data» (PDF).
- ^ a b Roche, Schinkel, Storey, Humphris & Guelden, «Speed of Light.» ISBN 0-7334-1527-X
- ^ Crr for large truck tires per Michelin
- ^ Green Seal 2003 Report
- ^ a b Gillespie ISBN 1-56091-199-9 p117
- ^ a b c Baker, Ira O., «Treatise on roads and pavements». New York, John Wiley, 1914. Stagecoach: Table 7, p. 28. Diameter: pp. 22-23. This book reports a few hundred values of rolling resistance for various animal-powered vehicles under various condition, mostly from 19th century data.
- ^ Hersey, subsection: «End of dark ages», p.261
- ^ Hersey, subsection: «Static rolling friction», p.266.
- ^ a b Williams, 1994, Ch. «Rolling contacts», eq. 11.1, p. 409.
- ^ Hersey, subsection: «Coulomb on wooden cylinders», p. 260
- ^ U.S. National Bureau of Standards, Fig. 1.13
- ^ Some[who?] think that smaller tire wheels, all else being equal, tend to have higher rolling resistance than larger wheels. In some laboratory tests, however, such as Greenspeed test results (accessdate = 2007-10-27), smaller wheels appeared to have similar or lower losses than large wheels, but these tests were done rolling the wheels against a small-diameter drum, which would theoretically remove the advantage of large-diameter wheels, thus making the tests irrelevant for resolving this issue. Another counter example to the claim of smaller wheels having higher rolling resistance can be found in the area of ultimate speed soap box derby racing. In this race, the speeds have increased as wheel diameters have decreased by up to 50%. This might suggest that rolling resistance may not be increasing significantly with smaller diameter within a practical range, if any other of the many variables involved have been controlled for. See talk page.
- ^ Zéhil, Gérard-Philippe; Gavin, Henri P. (2013). «Three-dimensional boundary element formulation of an incompressible viscoelastic layer of finite thickness applied to the rolling resistance of a rigid sphere». International Journal of Solids and Structures. 50 (6): 833–842. doi:10.1016/j.ijsolstr.2012.11.020.
- ^ Zéhil, Gérard-Philippe; Gavin, Henri P. (2013). «Simple algorithms for solving steady-state frictional rolling contact problems in two and three dimensions». International Journal of Solids and Structures. 50 (6): 843–852. doi:10.1016/j.ijsolstr.2012.11.021.
- ^ Zéhil, Gérard-Philippe; Gavin, Henri P. (2013). «Simplified approaches to viscoelastic rolling resistance». International Journal of Solids and Structures. 50 (6): 853–862. doi:10.1016/j.ijsolstr.2012.09.025.
- ^ «SAE MOBILUS». saemobilus.sae.org. doi:10.4271/06-11-02-0014. Retrieved 2021-04-19.
- ^ Sina, Naser; Hairi Yazdi, Mohammad Reza; Esfahanian, Vahid (2020-03-01). «A novel method to improve vehicle energy efficiency: Minimization of tire power loss». Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering. 234 (4): 1153–1166. doi:10.1177/0954407019861241. ISSN 0954-4070. S2CID 199099736.
- ^ Sina, Naser; Nasiri, Sayyad; Karkhaneh, Vahid (2015-11-01). «Effects of resistive loads and tire inflation pressure on tire power losses and CO2 emissions in real-world conditions». Applied Energy. 157: 974–983. doi:10.1016/j.apenergy.2015.04.010. ISSN 0306-2619.
- ^ «SAE MOBILUS». saemobilus.sae.org. doi:10.4271/06-11-02-0014. Retrieved 2021-04-19.
- ^ a b Roberts, Fig. 17: «Effect of torque transmission on rolling resistance», p. 71
- ^ Деев, p.30 including eq. (2.7) and Fig. 2.3
- ^ Астахов, Figs. 3.8, 3.9, 3.11, pp. 50-55. Hay, Fig. 60-2, p. 72 shows the same phenomena but has higher values for Crr and not reported here since the railroads in 2011 [1].
were claiming about the same value as Астахов - ^ Hersey, Table 6., p. 267
- ^ Per this assumption,
where
is the rolling resistance force and
is the normal load force on the wheel due to vehicle weight, and
is a constant. It can be readily shown by differentiation of
with respect to
using this rule that
- ^ Roberts, pp. 60-61.
- ^ [2] A Relationship between Tyre Pressure and Rolling Resistance Force under Different Vehicle Speed | Apiwat Suyabodha |Department of Automotive Engineering, Rangsit University, Lak-hok, Pathumthani, Thailand | 2017
- ^ [3] C. Michael Hogan, Analysis of Highway Noise, Journal of Soil, Air and Water Pollution, Springer Verlag Publishers, Netherlands, Volume 2, Number 3 / September, 1973
- ^ Gwidon W. Stachowiak, Andrew William Batchelor, Engineering Tribology, Elsevier Publisher, 750 pages (2000) ISBN 0-7506-7304-4
- ^ http://144.206.159.178/ft/200/607426/12614863.pdf[permanent dead link]
- ^ http://www.rubberchemtechnol.org/resource/1/rctea4/v3/i1/p19_s1?isAuthorized=no[permanent dead link]
- ^ a b c d «Schwalbe Tires: Rolling Resistance».
- ^ The Recumbent Bicycle and Human Powered Vehicle Information Center
- ^ U.S National Bureau of Standards p.? and Williams p.?
- ^ Roberts, «Effect of temperature», p.59
- ^ Астахов, p. 74, Although Астахов list these components, he doesn’t give the sum a name.
- ^ Шадур. Л. А. (editor). Вагоны (in Russian)(Railway cars). Москва, Транспорт, 1980. pp. 122 and figs. VI.1 p. 123 VI.2 p. 125
- ^ Association of American Railroads, Mechanical Division «Car and Locomotive Encyclopedia», New York, Simmons-Boardman, 1974. Section 14: «Axle journals and bearings». Almost all of the ads in this section are for the tapered type of bearing.
- ^ Астахов, Fig 4.2, p. 76
- ^ Statistics of railroads of class I in the United States, Years 1965 to 1975: Statistical summary. Washington DC, Association of American Railroads, Economics and Finance Dept. See table for Amtrak, p.16. To get the tons per passenger divide ton-miles (including locomotives) by passenger-miles. To get tons-gross/tons-net, divide gross ton-mi (including locomotives) (in the «operating statistics» table by the revenue ton-miles (from the «Freight traffic» table)
- Астахов П.Н. (in Russian) «Сопротивление движению железнодорожного подвижного состава» (Resistance to motion of railway rolling stock) Труды ЦНИИ МПС (ISSN 0372-3305). Выпуск 311 (Vol. 311). — Москва: Транспорт, 1966. – 178 pp. perm. record at UC Berkeley (In 2012, full text was on the Internet but the U.S. was blocked)
- Деев В.В., Ильин Г.А., Афонин Г.С. (in Russian) «Тяга поездов» (Traction of trains) Учебное пособие. — М.: Транспорт, 1987. — 264 pp.
- Hay, William W. «Railroad Engineering» New York, Wiley 1953
- Hersey, Mayo D., «Rolling Friction» Transactions of the ASME, April 1969 pp. 260–275 and Journal of Lubrication Technology, January 1970, pp. 83–88 (one article split between two journals) Except for the «Historical Introduction» and a survey of the literature, it is mainly about laboratory testing of mine railroad cast iron wheels of diameters 8″ to 24 done in the 1920s (almost a half century delay between experiment and publication).
- Hoerner, Sighard F., «Fluid dynamic drag», published by the author, 1965. (Chapt. 12 is «Land-Borne Vehicles» and includes rolling resistance (trains, autos, trucks).)
- Roberts, G. B., «Power wastage in tires», International Rubber Conference, Washington, D.C. 1959.
- U.S National Bureau of Standards, «Mechanics of Pneumatic Tires», Monograph #132, 1969–1970.
- Williams, J. A. Engineering tribology’. Oxford University Press, 1994.
External links[edit]
- Rolling Resistance and Fuel Saving
- temperature vs rolling resistance
- Simple roll-down test to measure Crr in cars and bikes
- Rolling Resistance Thresholds
Коэффициент
сопротивления качению является основным
показателем сил сопротивления, возникающих
при перекатывании колес по опорной
поверхности. Его значение зависит от
конструкции и технического состояния
шины, режима качения, типа и состояния
опорной поверхности.
На
дорогах с
твердым
покрытием основное значение имеет
конструкция шины, ее техническое
состояние и режим качения.
К
конструктивным факторам, определяющим
сопротивление качению, относятся:
конструкция каркаса (тип, расположение
нитей и число слоев корда), а также
толщина протектора. При прочих равных
условиях снижению коэффициента
сопротивления качению способствует:
радиальное расположение нитей корда,
уменьшение числа слоев корда, использование
низкогистерезисной резины и увеличение
размеров шины (прежде всего ее диаметра).
К
основным факторам технического состояния
шины, влияющим на сопротивление качению,
относятся: внутреннее давление воздуха
в шине и износ протектора по высоте. При
снижении внутреннего давления воздуха
(рw)
возрастают деформации шины, в результате
чего увеличиваются гистерезисные потери
и повышается коэффициент сопротивления
качению (рис. 3).
Увеличение
износа протектора по высоте, наоборот,
способствует снижению потерь в шине и
уменьшению коэффициента сопротивления
качению. При 100
% износе
протектора значение f
примерно на
20 — 25% ниже,
чем у новой шины.
К
основным факторам режима качения колеса
можно отнести, прежде всего, величину
крутящего момента и скорость движения.
Рис.
3.
Влияние давления воздуха в шине на
коэффициент
сопротивления
качению
При
увеличении крутящего момента коэффициент
немного увеличивается, т.к. шина при
этом деформируется не только в вертикальном
но и по окружности. При большой величине
передаваемого момента элементы протектора
проскальзывают по дороге, и на трение
в области контакта также затрачивается
дополнительная мощность. Однако, как
показывают эксперименты, значительный
рост коэффициента сопротивления качению
наблюдается лишь при скоростях движения
свыше
50 — 60 км/ч.
а интенсивный
— свыше 100
км/ч. Для определения его величины была
предложена проф. Н.А. Яковлевым эмпирическая
формула:
f
= fo(1
+ Va/1500), (8)
где
fo
— коэффициент сопротивления качению
при относительно малой скорости движения;
Vа
— скорость
движения автомобиля, м/с.
При
движении автомобиля по дорогам с твердым
покрытием коэффициент f
немного увеличивается с уменьшением
давления воздуха в шине. Наглядное
представление о влиянии типа и состояния
опорной поверхности на сопротивление
качения дает табл. 1.
Таблица 1
Коэффициент сопротивления качению для различных дорог
|
Тип |
Состояние опорной поверхности |
F |
|
Асфальтобетон |
хорошее |
0,012-0,018 |
|
Булыжник |
хорошее |
0,025-0,030 |
|
Грунтовая |
сухая укатанная после дождя |
0,025-0,035 0,050-0,150 |
|
Песок |
сухой сырой |
0,150-0,300 0,060-0,150 |
|
Снег |
укатанный целина |
0,030-0,050 0,180-0,250 |
|
Лед |
— |
0,150-0,030 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Сопротивление качению, иногда называемое трением качения или сопротивлением качению, представляет собой силу, противодействующую движение, когда тело (например, мяч, шина или колесо ) катится по поверхности. Это в основном вызвано неэластичными эффектами; то есть не вся энергия, необходимая для деформации (или движения) колеса, дорожного полотна и т. д., восстанавливается при снятии давления. Двумя формами этого являются гистерезисные потери (см. ниже ) и постоянная (пластическая) деформация объекта или поверхности (например, грунта). Другая причина сопротивления качению заключается в проскальзывании между колесом и поверхностью, которое рассеивает энергию. Обратите внимание, что только последний из этих эффектов включает в себя трение, поэтому название «трение качения» в некоторой степени неверно.
По аналогии с трением скольжения сопротивление качению часто выражается как коэффициент, умноженный на нормальную силу. Этот коэффициент сопротивления качению, как правило, намного меньше, чем коэффициент трения скольжения.
Любое двигающееся накатом колесное транспортное средство будет постепенно замедляться из-за сопротивления качению, включая сопротивление подшипников, но поезд вагон со стальными колесами, движущийся по стальным рельсам, будет катиться дальше, чем автобус той же массы с резиновыми шинами, движущийся по асфальту. Факторами, влияющими на сопротивление качению, являются (степень) деформации колес, деформация поверхности дорожного полотна и движение под поверхностью. Дополнительные способствующие факторы включают диаметр колеса, нагрузку на колесо, поверхностное сцепление, скольжение и относительное микропроскальзывание между поверхностями контакта. Потери из-за гистерезиса также сильно зависят от свойств материала колеса или шины и поверхности. Например, резиновая шина будет иметь более высокое сопротивление качению на асфальтированной дороге, чем стальное железнодорожное колесо на стальном рельсе. Кроме того, песок на земле даст большее сопротивление качению, чем бетон. Единственный коэффициент сопротивления качению не зависит от скорости.
Содержание
- 1 Основная причина
- 2 Определения
- 3 Коэффициент сопротивления качению
- 4 Измерение
- 5 Физические формулы
- 6 Примеры коэффициента сопротивления качению
- 7 Зависимость от диаметра
- 7.1 Дилижансы и железные дороги
- 7.2 Пневматические шины
- 8 Зависимость от приложенного крутящего момента
- 8.1 Все колеса
- 8.2 Железнодорожные стальные колеса
- 8.3 Пневматические шины
- 9 Зависимость от нагрузки на колеса
- 9.1 Железнодорожные стальные колеса
- 9.2 Пневматические шины
- 10 Зависимость от кривизны проезжей части
- 10.1 Общие положения
- 11 Звуковые эффекты
- 12 Факторы, влияющие на шины
- 13 Железные дороги: компоненты сопротивления качению
- 14 Сравнение сопротивления качению дорожных транспортных средств и поездов
- 15 См. Также
- 16 Ссылки
- 17 Внешние ссылки
Основная причина
Основной причиной сопротивления качению пневматической шины является гистерезис :
Характеристика деформируемый материал, у которого энергия деформации больше, чем энергия восстановления. Резиновая смесь в шине проявляет гистерезис. По мере того как шина вращается под весом транспортного средства, она испытывает повторяющиеся циклы деформации и восстановления, и она рассеивает гистерезисные потери энергии в виде тепла. Гистерезис является основной причиной потерь энергии, связанных с сопротивлением качению, и объясняется вязкоупругими характеристиками резины.
- — Национальная академия наук
Этот основной принцип проиллюстрирован на рисунке цилиндров качения. Если два одинаковых цилиндра прижать друг к другу, то контактная поверхность будет плоской. При отсутствии поверхностного трения контактные напряжения нормальны (т.е. перпендикулярны) контактной поверхности. Рассмотрим частицу, которая входит в область контакта с правой стороны, проходит через пятно контакта и уходит с левой стороны. Первоначально его вертикальная деформация увеличивается, чему препятствует эффект гистерезиса. Следовательно, создается дополнительное давление, чтобы избежать взаимного проникновения двух поверхностей. В дальнейшем его вертикальная деформация уменьшается. Этому снова препятствует эффект гистерезиса. В этом случае это снижает давление, необходимое для разделения двух тел.
В результате распределение давления асимметрично и смещено вправо. Линия действия (совокупной) вертикальной силы больше не проходит через центры цилиндров. Это означает, что возникает момент, который имеет тенденцию замедлять перекатывающее движение.
Материалы с большим эффектом гистерезиса, такие как резина, которая отскакивает медленно, демонстрируют большее сопротивление качению, чем материалы с небольшим эффектом гистерезиса, которые отскакивают быстрее и полнее, такие как сталь или диоксид кремния. Шины с низким сопротивлением качению обычно включают диоксид кремния вместо технического углерода в состав протектора для уменьшения низкочастотного гистерезиса без снижения тягового усилия. Обратите внимание, что железные дороги также имеют гистерезис в конструкции дорожного полотна.
Определения
В широком смысле удельное «сопротивление качению» (для транспортных средств) — это сила на единицу веса транспортного средства, необходимая для перемещения транспортного средства на ровной поверхности с постоянной низкой скоростью, где аэродинамическое сопротивление (сопротивление воздуха) незначительно, а также при отсутствии тяговых (моторных) сил или тормозов. Другими словами, автомобиль двигался бы по инерции, если бы не сила, поддерживающая постоянную скорость. Этот широкий смысл включает сопротивление подшипника ступицы колеса, энергию, рассеиваемую при вибрации и колебаниях дорожного полотна и транспортного средства, а также скольжение колеса по поверхности дорожного полотна (тротуару или рельсу).
Но есть еще более широкий смысл, который может включать в себя потери энергии из-за пробуксовки колес из-за крутящего момента, передаваемого от двигателя. Это включает в себя увеличенную мощность, требуемую из-за увеличения скорости колес, когда тангенциальная скорость ведущего колеса (колес) становится больше, чем скорость транспортного средства из-за проскальзывания. Поскольку мощность равна силе, умноженной на скорость, и скорость колеса увеличилась, требуемая мощность соответственно увеличилась.
Чистое «сопротивление качению» для поезда — это то, что возникает из-за деформации и возможного незначительного скольжения при контакте колеса с дорогой. Для резиновой шины аналогичная потеря энергии происходит по всей шине, но она все еще называется «сопротивлением качению». В широком смысле «сопротивление качению» включает сопротивление подшипника ступицы колеса, потерю энергии при сотрясении как дорожного полотна (и земли под ним), так и самого транспортного средства, а также при скольжении колеса при контакте дороги и рельса. Учебники по железной дороге, кажется, охватывают все эти силы сопротивления, но не называют их сумму «сопротивлением качению» (в широком смысле), как это делается в этой статье. Они просто суммируют все силы сопротивления (включая аэродинамическое сопротивление) и называют эту сумму базовым сопротивлением поезда (или тому подобное).
Поскольку сопротивление качению на железной дороге в широком смысле может быть в несколько раз больше, чем просто чистое сопротивление качению. Приведенные значения сопротивления качению могут серьезно противоречить друг другу, поскольку они могут основываться на разных определениях «сопротивления качению». Разумеется, двигатели поезда должны обеспечивать энергию для преодоления этого сопротивления качению в широком смысле.
Для шин сопротивление качению определяется как энергия, потребляемая шиной на единицу пройденного пути. Это также называется трением качения или сопротивлением качения. Это одна из сил, препятствующих движению водителя. Основная причина этого заключается в том, что, когда шины движутся и касаются поверхности, поверхность меняет форму и вызывает деформацию шины.
Для шоссейных транспортных средств, очевидно, что при сотрясении проезжей части рассеивается некоторая энергия. (и землю под ним), сотрясение самого транспортного средства и скольжение шин. Но, за исключением дополнительной мощности, необходимой из-за крутящего момента и трения в колесном подшипнике, нечистое сопротивление качению, по-видимому, не исследовалось, возможно потому, что «чистое» сопротивление качению резиновой шины составляет несколько единиц. раз выше, чем сопротивление, которое не учитывалось.
Коэффициент сопротивления качению
«Коэффициент сопротивления качению» определяется следующим уравнением:
- F = C rr N { displaystyle F = C_ {rr} N}
- где
- F { displaystyle F}
— сила сопротивления качению (показанная как R { displaystyle R}
на рисунке 1.),
- C rr { displaystyle C_ {rr}}
— безразмерный коэффициент сопротивления качению или коэффициент трения качения (CRF ), а
- N { displaystyle N}
— это нормальная сила, сила, перпендикулярная поверхности, по которой катится колесо.
- F { displaystyle F}
C rr { displaystyle C_ {rr}}







Выше показано сопротивление, пропорциональное C rr { displaystyle C_ {rr}}


Измерение
Существует как минимум две популярные модели для расчета сопротивления качению.
- «Коэффициент сопротивления качению (RRC). Значение силы сопротивления качению, деленное на нагрузку на колесо. Общество автомобильных инженеров (SAE) разработало методы испытаний для измерения RRC шин. Эти испытания (SAE J1269 и SAE J2452 ) обычно выполняются на новых шинах. При измерении с использованием этих стандартных методов испытаний, для большинства новых легковых шин значения RRC варьируются от 0,007 до 0,014 ». В случае велосипедных шин достигаются значения от 0,0025 до 0,005. Эти коэффициенты измеряются на катках, измерителями мощности на дорожном покрытии или с. В последних двух случаях необходимо вычесть влияние сопротивления воздуха или испытания проводить на очень низких скоростях.
- Коэффициент сопротивления качению b, который имеет размер длина, равен приблизительно (из-за малоуглового приближения из cos (θ) = 1 { displaystyle cos ( theta) = 1}
) равным значению сила сопротивления качению, умноженная на радиус колеса, деленное на нагрузку на колесо.
- используется для проверки сопротивления качению в Европе.
Результаты этих испытаний могут быть трудными для широкую публику получить, поскольку производители предпочитают рекламировать «комфорт» и «производительность».
Физические формулы
Коэффициент сопротивления качению для медленного жесткого колеса по идеально упругой поверхности, не скорректированный по скорости, может быть рассчитан как
- C rr = z / d { displaystyle C_ {rr} = { sqrt {z / d}}}
- где
- z { displaystyle z}
— глубина погружения
- d { displaystyle d}
— диаметр жесткого колеса
- z { displaystyle z}
Эмпирическая формула для C rr { displaystyle C_ {rr}}
- C rr = 0,0048 (18 / D) 1 2 (100 / W) 1 4 = 0,0643988 WD 2 4 { displaystyle C_ {rr} = 0,0048 (18 / D) ^ { frac {1} {2 }} (100 / Вт) ^ { frac {1} {4}} = { frac {0.0643988} { sqrt [{4}] {WD ^ {2}}}}}
- где
- D { displaystyle D}
— диаметр колеса в дюймах
- W { displaystyle W}
— нагрузка на колесо в фунтах-силах
- D { displaystyle D}
В качестве альтернативы используя C rr { displaystyle C_ {rr}}

- F = N br { displaystyle F = { frac {Nb} {r}}}
- где
- F { displaystyle F}
— сила сопротивления качению (показанная на рисунке 1),
- r { displaystyle r}
— радиус колеса,
- b { displaystyle b}
— это коэффициент сопротивления качению или коэффициент трения качения с размером длины, а
- N { displaystyle N}
— нормальная сила (равная W, не R, как показано на рисунке 1).
- F { displaystyle F}
Вышеприведенное уравнение, в котором сопротивление обратно пропорционально радиусу r. похоже, основан на дискредитированном «законе Кулона» (ни закон обратных квадратов Кулона, ни закон трения Кулона) (нуждается в цитировании). См. Зависимость от диаметра. Приравнивая это уравнение к силе, приходящейся на коэффициент сопротивления качению, и решая для b, получаем b = C rr · r. Следовательно, если источник дает коэффициент сопротивления качению (C rr) как безразмерный коэффициент, его можно преобразовать в b, имеющий единицы длины, умножив C rr на радиус колеса r.
Примеры коэффициента сопротивления качению
Таблица примеров коэффициента сопротивления качению: [3]
| Crr | b | Описание |
| от 0,0003 до 0,0004 | «Чистое сопротивление качению» Колесо из железнодорожной стали на стальном рельсе | |
| от 0,0010 до 0,0015 | 0,1 мм | Шарикоподшипники из закаленной стали на стали |
| от 0,0010 до 0,0024 | 0,5 мм | Железнодорожное стальное колесо на стальном рельсе. Легковой железнодорожный вагон около 0,0020 |
| 0,0019 до 0,0065 | Чугунные колеса шахтных вагонов на стальном рельсе | |
| 0,0022 до 0,0050 | Серийные велосипедные шины при давлении 120 фунтов на квадратный дюйм (8,3 бар) и 50 км / ч (31 миль в час), измерено на роликах | |
| 0,0025 | Special Michelin солнечный автомобиль / эко-марафон шины | |
| 0,0050 | Грязные трамвайные рельсы (стандарт) с прямыми и изгибами | |
| 0,0045 до 0,0080 | Большой грузовик (Полу) шины | |
| 0,0055 | Типичные велосипедные шины BMX, используемые для солнечных автомобилей | |
| 0,0062 до 0,0150 | Размеры автомобильных шин | |
| от 0,0100 до 0,0150 | Обычные автомобильные шины на бетоне | |
| от 0,0385 до 0,0730 | дилижанс (XIX век) на грунтовой дороге. Мягкий снег на дороге в худшем случае. | |
| 0,3000 | Обычные автомобильные шины по песку |
Например, в условиях земной силы тяжести автомобилю массой 1000 кг по асфальту потребуется сила около 100 ньютонов для качения (1000 кг × 9,81 м / с × 0,01 = 98,1 Н).
Зависимость от диаметра
Дилижансы и железные дороги
Согласно Дюпюи (1837) сопротивление качению (колесных вагонов с деревянными колесами с железными шинами) приблизительно обратно пропорционально корень квадратный из диаметра колеса. Это правило было экспериментально подтверждено для чугунных колес (диаметром 8–24 дюймов) на стальном рельсе и для колес тележек 19 века. Но есть и другие тесты колес тележки, которые не согласуются. Теория качения цилиндра по упругой дороге также дает то же самое правило. Они противоречат более ранним (1785 г.) испытаниям Кулона катания деревянных цилиндров, в которых Кулон сообщил, что сопротивление качению обратно пропорционально диаметру колеса (известное как «закон Кулона»).. Однако этот оспариваемый (или неправильно применяемый) «закон Кулона» все еще встречается в справочниках.
Пневматические шины
Сообщается, что для пневматических шин на твердом покрытии влияние диаметра на сопротивление качению незначительно (в пределах практического диапазона диаметров).
Зависимость от приложенного крутящего момента
Приводной крутящий момент T { displaystyle T}

- T = V s Ω R r { displaystyle T = { frac {V_ {s}} { Омега}} R_ {r}}
- , где
- V s { displaystyle V_ {s}}
— линейная скорость тела (на оси), а
- Ω { displaystyle Omega}
его скорость вращения.
- V s { displaystyle V_ {s}}
Стоит отметить, что V s / Ω { displaystyle V_ {s} / Omega}
Все колеса
«Приложенный крутящий момент» может быть либо крутящим моментом, приложенным двигателем (часто через трансмиссию ), либо тормозным крутящий момент прилагается тормоза (включая рекуперативное торможение ). Такие моменты приводят к рассеянию энергии (выше, чем из-за основного сопротивления качению свободно катящегося, не ведущего, не тормозящего колеса). Эти дополнительные потери частично связаны с тем, что колесо имеет некоторую пробуксовку, а в случае пневматических шин происходит больший прогиб боковин из-за крутящего момента. Скольжение определяется таким образом, что 2% -ное скольжение означает, что окружная скорость ведущего колеса превышает скорость транспортного средства на 2%.
Небольшой процент скольжения может привести к гораздо большему процентному увеличению сопротивления качению. Например, для пневматических шин проскальзывание 5% может привести к увеличению сопротивления качению на 200%. Частично это связано с тем, что тяговое усилие, прилагаемое во время этого скольжения, во много раз превышает силу сопротивления качению, и, таким образом, прилагается гораздо больше мощности на единицу скорости (вспомните, мощность = сила x скорость так что мощность на единицу скорости есть просто сила). Таким образом, даже небольшое увеличение окружной скорости в процентах из-за скольжения может привести к потере тягового усилия, которая может даже превысить потерю мощности из-за основного (обычного) сопротивления качению. Для железных дорог этот эффект может быть еще более выраженным из-за низкого сопротивления качению стальных колес.
Железнодорожные стальные колеса
Чтобы применить тягу к колесам, необходимо некоторое проскальзывание колеса. Для российских поездов, поднимающихся на подъем, это скольжение обычно составляет от 1,5% до 2,5%.
Скольжение (также известное как проскальзывание ) обычно примерно прямо пропорционально тяговому усилию. Исключением является то, что тяговое усилие настолько велико, что колесо приближается к значительному пробуксовыванию (более нескольких процентов, как обсуждалось выше), тогда скольжение быстро увеличивается с увеличением тягового усилия и перестает быть линейным. При чуть более высоком прилагаемом тяговом усилии колесо выходит из-под контроля, и сцепление падает, в результате чего колесо вращается еще быстрее. Это тип проскальзывания, который можно наблюдать невооруженным глазом — например, скольжение в 2% для тяги наблюдается только с помощью приборов. Такое быстрое скольжение может привести к чрезмерному износу или повреждению.
Пневматические шины
Сопротивление качению значительно увеличивается с приложенным крутящим моментом. При высоких крутящих моментах, когда к дороге прилагается тангенциальная сила, составляющая примерно половину веса транспортного средства, сопротивление качению может утроиться (увеличение на 200%). Частично это связано с проскальзыванием примерно на 5%. Увеличение сопротивления качению с приложенным крутящим моментом не является линейным, а увеличивается с большей скоростью, когда крутящий момент становится выше.
Зависимость от нагрузки на колесо
Железнодорожные стальные колеса
Коэффициент сопротивления качению Crr значительно уменьшается по мере увеличения веса железнодорожного вагона на каждое колесо. Например, у пустого российского грузового вагона Crr было примерно вдвое больше, чем у загруженного вагона (Crr = 0,002 против Crr = 0,001). Та же «экономия на масштабе» проявляется при испытании шахтных вагонов. Теоретический Crr для жесткого колеса, катящегося по упругому дорожному полотну, показывает Crr, обратно пропорциональный квадратному корню из нагрузки.
Если Crr сам по себе зависит от нагрузки на колесо по правилу обратного квадратного корня, то для увеличения при нагрузке 2% сопротивление качению увеличивается только на 1%.
Пневматические шины
Для пневматических шин направление изменения Crr (коэффициента сопротивления качению) зависит от того, покрыта ли шина инфляция увеличивается с увеличением нагрузки. Сообщается, что если внутреннее давление увеличивается с нагрузкой в соответствии с (неопределенным) «графиком», то 20% -ное увеличение нагрузки снижает Crr на 3%. Но если давление накачки не изменяется, то увеличение нагрузки на 20% приводит к увеличению Crr на 4%. Конечно, это увеличит сопротивление качению на 20% из-за увеличения нагрузки плюс 1,2 x 4% из-за увеличения Crr, что приведет к увеличению сопротивления качению на 24,8%.
Зависимость от кривизны проезжей части
Общее
Когда транспортное средство (автотранспорт или железная дорога поезд ) движется по кривой сопротивление качению обычно увеличивается. Если кривая не имеет наклона, чтобы точно противодействовать центробежной силе равной и противоположной центростремительной силой из-за наклона, тогда будет чистая несбалансированная боковая нагрузка на автомобиль. Это приведет к увеличению сопротивления качению. Крен также известен как «наклон» или «наклон» (не путать с перекосом на направляющей ). Для железных дорог это называется сопротивление кривой, но для дорог оно (по крайней мере один раз) называлось сопротивлением качению из-за прохождения поворотов.
Звуковые эффекты
Трение качения генерирует звуковую (колебательную) энергию, поскольку механическая энергия преобразуется в эту форму энергии за счет трения. Одним из наиболее распространенных примеров трения качения является движение шин автомобилей по проезжей части, процесс, в результате которого в качестве побочного продукта генерируется звук. Звук, издаваемый шинами легковых и грузовых автомобилей при катании (особенно заметный на скоростях шоссе), в основном связан с ударом протектора шин и сжатием (и последующей декомпрессией) воздуха, временно захваченного протекторами.
Факторы, влияющие на шины
На величину сопротивления качению, которое создает шина, влияют несколько факторов:
- Как упоминалось во введении: радиус колеса, скорость движения вперед, сцепление с поверхностью и относительное микростолзание.
- Материал — различные наполнители и полимеры в составе шины могут улучшить сцепление с дорогой при одновременном снижении гистерезиса. Замена некоторого количества технического углерода более дорогим кремнезем-силаном — один из распространенных способов снижения сопротивления качению. Было показано, что использование экзотических материалов, включая наноглину, снижает сопротивление качению в высокоэффективных резиновых шинах. Растворители также могут использоваться для разбухания твердых шин, что снижает сопротивление качению.
- Размеры — сопротивление качению в шинах связано с изгибом боковин и площадью контакта шины. Например, при одинаковом давлении шире велосипедные шины меньше прогибаются в боковинах при качении и, следовательно, имеют меньшее сопротивление качению (хотя и более высокое сопротивление воздуха).
- Степень накачивания — меньшее давление в шинах приводит к большему изгибу боковин и более высокое сопротивление качению. Это преобразование энергии в боковинах увеличивает сопротивление, а также может привести к перегреву и, возможно, сыграло свою роль в печально известных Ford Explorer авариях с опрокидыванием.
- Из-за накачивания шин (например, велосипедных шин) нельзя снизить общее сопротивление качению, так как шина может прыгать по поверхности дороги. Приносится в жертву тяговое усилие, и общее трение качения не может быть уменьшено по мере изменения скорости вращения колеса и увеличения проскальзывания.
- Отклонение боковой стенки не является прямым измерением трения качения. Высококачественная шина с высококачественным (и гибким) каркасом обеспечит большую гибкость на потерю энергии, чем дешевая шина с жесткой боковиной. Опять же, на велосипеде качественная шина с гибким каркасом будет катиться легче, чем дешевая шина с жестким каркасом. Точно так же, как отмечают шины Goodyear для грузовых автомобилей, шина с каркасом «экономия топлива» будет способствовать экономии топлива в течение многих сроков службы протектора (т.е. при восстановлении протектора), в то время как шина с рисунком протектора «экономия топлива» принесет пользу только до тех пор, пока протектор не износится.
- В шинах толщина и форма протектора имеют прямое отношение к сопротивлению качению. Чем толще и рельефнее протектор, тем выше сопротивление качению. Таким образом, «самые быстрые» велосипедные шины имеют очень маленький протектор, и тяжелые грузовики получают лучшую экономию топлива, поскольку протектор шины изнашивается.
- Эффекты диаметра кажутся можно пренебречь при условии твердого покрытия и ограниченного диапазона диаметров. См. Зависимость от диаметра..
- Практически все мировые рекорды скорости были установлены на относительно узких колесах, вероятно, из-за их аэродинамических преимуществ на высокой скорости, что гораздо менее важно на обычных скоростях.
- Температура: Как для сплошных, так и для пневматических шин сопротивление качению снижается с повышением температуры (в пределах диапазона температур: т.е. существует верхний предел этого эффекта). При повышении температуры от 30 ° C до 70 ° C сопротивление качению снизился на 20-25%. Утверждается, что гонщики нагревают свои шины перед гонками.
Железные дороги: компоненты сопротивления качению
В широком смысле сопротивление качению можно определить как сумму компонентов):
- Потери крутящего момента в подшипниках колеса.
- Чистое сопротивление качению.
- Скольжение колеса по рельсу.
- Потеря энергии на дорожное полотно (и землю).
- Потеря энергии к колебаниям железнодорожного подвижного состава.
Потери крутящего момента в подшипнике колеса можно измерить как сопротивление качению на ободе колеса, Crr. На железных дорогах обычно используются роликовые подшипники цилиндрической (Россия) или конической (США). Удельное сопротивление качению российских подшипников зависит как от нагрузки на колесо, так и от скорости. Сопротивление качению подшипников ступицы самое низкое при высоких нагрузках на ось и средних скоростях 60–80 км / ч при Crr 0,00013 (нагрузка на ось 21 тонна). Для порожних грузовых вагонов с осевой нагрузкой 5,5 т Crr увеличивается до 0,00020 при 60 км / ч, но на низкой скорости 20 км / ч он увеличивается до 0,00024, а на высокой скорости (для грузовых поездов) 120 км / ч. это 0,00028. Полученный выше Crr добавляется к Crr других компонентов, чтобы получить общий Crr для колес.
Сравнение сопротивления качению шоссейных транспортных средств и поездов
Сопротивление качению стальных колес по стальному рельсу поезда намного меньше, чем сопротивление качению колес с резиновыми шинами автомобиля или грузовика. Вес поездов сильно различается; в некоторых случаях они могут быть намного тяжелее на пассажира или на тонну нетто груза, чем автомобиль или грузовик, но в других случаях они могут быть намного легче.
В качестве примера очень тяжелого пассажирского поезда в 1975 году пассажирские поезда Amtrak весили немногим более 7 тонн на пассажира, что намного тяжелее, чем в среднем чуть более одной тонны на пассажира для автомобиля. Это означает, что для пассажирского поезда Amtrak в 1975 году большая часть экономии энергии за счет более низкого сопротивления качению была потеряна из-за его большего веса.
Примером очень легкого высокоскоростного пассажирского поезда является Синкансэн серии N700, который весит 715 тонн и перевозит 1323 пассажира, в результате чего вес на одного пассажира составляет около полтонны.. Этот меньший вес на пассажира в сочетании с более низким сопротивлением качению стальных колес по стальному рельсу означает, что синкансэн N700 намного более энергоэффективен, чем обычный автомобиль.
Что касается грузовых перевозок, CSX в 2013 году провела рекламную кампанию, в которой утверждалось, что их грузовые поезда перемещают «тонну груза на 436 миль на галлоне топлива», тогда как некоторые источники утверждают, что грузовики перемещают тонну груза на расстоянии 130 миль на галлон топлива, что указывает на то, что поезда в целом более эффективны.
См. Также
Литература
- Астахов П.Н. «Сопротивление движению железнодорожного подвижного состава» Труды ЦНИИ МПС (ISSN 0372-3305). Выпуск 311 (Том 311). — Москва: Транспорт, 1966. — 178 с. перм. запись в Калифорнийском университете в Беркли (В 2012 году полный текст был в Интернете, но США были заблокированы)
- Деев В.В., Ильин Г.А., Афонин Г.С. «Тяга поездов» Учебное пособие. — М.: Транспорт, 1987. — 264 с.
- Хэй, Уильям У. «Railroad Engineering» Нью-Йорк, Вили 1953
- Херси, Мэйо Д., «Роллинг трение». ASME, апрель 1969 г., стр. 260–275 и Journal of Lubrication Technology, январь 1970 г., стр. 83–88 (одна статья разделена между двумя журналами) За исключением «Исторического введения» и обзора литературы, в основном речь идет о лабораторные испытания чугунных колес шахтных железных дорог диаметром от 8 ″ до 24, проведенные в 1920-х годах (почти полвека задержка между экспериментом и публикацией).
- Hoerner, Sighard F., «Fluid dynamic drag», опубликовано автор, 1965. (Глава 12 — «Наземные транспортные средства» и включает сопротивление качению (поезда, автомобили, грузовики).)
- Робертс, Великобритания, «Потери мощности в шинах», Международная конференция по резине, Вашингтон, округ Колумбия, 1959.
- Национальное бюро стандартов США, «Механика пневматических шин», Монография № 132, 1969–1970 гг.
- Уильямс, Дж. А. Инженерная трибология ». Oxford University Press, 1994.
Внешние ссылки
| На Викискладе есть материалы, связанные с сопротивлением качению. |
3.1. Качение колеса
Энергия топлива, сжигаемого в двигателе, преобразуется в тяговую силу на колесе, которая расходуется на преодоление ряда сил сопротивления движению машины. В общем случае движения машины различают действие сил сопротивления качению Рf, подъему Рi; воздушной среды Рω движению прицепа Ркр силы инерции Рj. Рассмотрим их на примере движения автомобиля.
Сила сопротивления качению Рf возникает на поверхности контакта колеса с дорогой. Она существует при всех случаях движения автомобиля, в то время как остальные силы сопротивления появляются только при определенных режимах движения.
Сила сопротивления качению зависит от деформации шины и полотна дороги, трения шин о грунт. Основное значение имеет деформация шин и дороги. Равнодействующая элементарных сил, действующих со стороны дороги на колесо в области контакта, называется реакцией дороги. Реакцию дороги (рис. 3.1) в общем случае можно представить в виде трех составляющих реакций: нормальной Z перпендикулярной к дороге; касательной X, действующейв плоскости дороги и в плоскости вращения колеса, и поперечной Y, действующей в плоскости дороги и перпендикулярной плоскости вращения колеса.

Рис. 3.1. Реакция дороги, действующая на колесо автомобиля:
Рх — продольная сила; Рy — поперечная сила; Рz — вертикальная сила; R — горизонтальная реакция дороги
Нормальная реакция дороги Z возникает в результате действия на колесо вертикальной силы Рz .
Если на колесо кроме вертикальной силы Рz действуют продольная Рх и поперечная Рy силы, то в области контакта возникает горизонтальная реакция R дороги, действующая под углом к плоскости вращения колеса,

Процессы, происходящие при деформации шины и при качении колеса на разных поверхностях, имеют сложный характер. Рассмотрим схемы, представленные на рис. 3.2.

Рис. 3.2. Схемы деформации шины и качения колеса:
а — качение деформируемого колеса по твердой дороге; б — то же, по мягкой; X — нормальная реакция дороги; аш — смещение реакции Z относительно оси колеса, вызванное деформацией шины; А, А’ — точки пересечения вертикальной оси колеса и плоскости действия касательной реакции X дороги; X — касательная реакция дороги; Рz — вертикальная сила; М — вращающий момент колеса; Рх — толкающая сила; rд — динамический радиус колеса; dZ — элементарная нормальная реакция дороги; dRд— элементарная реакция дороги; Rд — суммарная реакция дороги; Yд— угол наклона реакции Rд; ад — смещение нормальной реакции Z относительно оси колеса, вызванное деформацией грунта; а — суммарное смещение реакции Z относительно оси колеса; → — напрааление действия сил и реакций
При качении упругого колеса по горизонтальной твердой дороге элементарные нормальные реакции dZ дороги и их равнодействующая расположены вертикально (рис. 3.2, а).
Во время качения колеса между частями шины при ее деформации возникают силы внутреннего трения и выделяющаяся при этом теплота рассеивается, т.е. происходит потеря энергии. В результате этого деформации в передней части шины и соответственно элементарные нормальные реакции в передней части поверхности контакта с дорогой увеличиваются, а в задней части уменьшаются. Это приводит к тому, что равнодействующая нормальной реакции дороги Z смещается относительно вертикального диаметра колеса вперед на расстояние аш, м. Смещение возрастает при увеличении числа слоев корда шины, толщины протектора и ширины обода колеса и уменьшается при повышении давления воздуха в шине.
В результате смещения точки приложения нормальной реакции возникает реактивный момент Мр = Zaш, препятствующий качению колеса. Для уравновешивания этого момента необходимо или к колесу приложить равный, но противоположно направленный вращающий момент М, Н*м, или к оси колеса подвести толкающую силу Рх, Н, равную касательной реакции X дороги, я в ляющейся силой сопротивления качению колеса.
Из условия равенства моментов, создаваемых реакцией Z и толкающей силой Рх относительно точки А, находим значение силы Рх, Н:

где rд — динамический радиус качения колеса, м.
На твердой дороге точка А соответствует центру опорной поверхности колеса.
При качении деформируемого колеса по мягкой дороге (рис. 3.2, б) энергия затрачивается на преодоление внутреннего трения в шине и деформацию дороги. Шина под действием вертикальной нагрузки вдавливается в грунт и, спрессовывая отдельные его частицы, образует колею.
Элементарные реакции дороги dRд в каждой точке контакта шины с дорогой перпендикулярны поверхности контакта и расположены наклонно. Поэтому и суммарная реакция Rд наклонена к вертикали под некоторым углом Yд.
При образовании колеи энергия затрачивается при накатывании шины на деформируемый грунт, что приводит к увеличению элементарных реакций dRд в передней части поверхности контакта и уменьшению их в задней. В результате точка приложения реакции Rд дороги смещается вперед относительно вертикального диаметра колеса на величину а, м. Это смещение можно представить как сумму смещения аш, вызванного затратами энергии при деформации шины, и смещения ад обусловленного затратами энергии при деформации грунта в процессе образования колеи, т. е. а = аш + ад.
Если колесо катится под действием толкающей силы Рх или вращающего момента М, то из уравнения моментов, создаваемых силами Z и Рх относительно точки А’, получим значение толкающей силы Рх, Н:

где f — коэффициент сопротивления качению.
Коэффициент сопротивления качению — это отношение

При качении упругого колеса по горизонтальной твердой дороге а = аш.
Коэффициент сопротивления качению численно равен отношению смещения а реакции дороги Z к динамическому радиусу rд колеса или отношению толкающей силы Рх, вызывающей равномерное качение колеса, к нормальной реакции дороги Z
Сумма сил сопротивления качению всех колес автомобиля определяет общую силу сопротивления качению Рf, которая при равномерном прямолинейном движении автомобиля будет равна суммарной толкающей силе ∑ Рх на всех колесах, следовательно,

Так как нормальная реакция Z равна вертикальной силе Рz, действующей на колесо, то момент сопротивления качению колес автомобиля составит, Н*м:

Поскольку суммарная вертикальная сила ∑ Рz, действующая на колеса, равна весу машины G, Н, то сила сопротивления качению
Pf = Gf
Значения а и rд зависят от величины деформации шины и грунта, следовательно, и значения f изменяются в зависимости от состояния поверхности качения и типа колеса. При этом большое влияние оказывает давление в шинах.
Также на величину коэффициента f сопротивления качению оказывают влияние скорость у движения автомобиля и значение передаваемого колесом вращающего момента М. При малой скорости (до 10… 15 м/с) коэффициент сопротивления качению можно считать постоянным, равным f0 (рис. 3.3, а). В случае движения автомобиля с большой скоростью он возрастает, так как шина не успевает полностью распрямиться в области контакта, вследствие чего возвращается не вся энергия, затраченная на деформацию шины.

Рис. 3.3. Изменение коэффициента сопротивления качению f упругого колеса под действием разных факторов:
а — влияние скорости автомобиля u, б — внутреннего давления в шине рш в — вращающего момента М, передаваемого колесом ; f — средний коэффициент сопротивления качению ; f0, — то же, при малой (менее 15 м/с) скорости автомобиля.
Кроме того, при повышении скорости деформации возрастает внутреннее трение в шине, также вызывающее увеличение коэффициента f.
Для определения коэффициента сопротивления качению в за висимости от скорости движения u, м/с, пользуются эмпирической формулой

где fо — коэффициент сопротивления качению в зависимости от типа дороги (при малой скорости движения автомобиля) (табл. 3.1).
Таблица 3.1
Коэффициент сопротивления качению в зависимости от типа дороги
|
Тип дороги |
f0 при u < 15 м/с |
f (среднее значение) |
|
С асфальтовым и цементобетонным покрытием: в отличном состоянии в удовлетворительном состоянии |
0,014 0,018 |
0,014…0.018 0,018….0.020 |
|
Булыжная мостовая |
0,025 |
0,023…0,030 |
|
С гравийным покрытием |
0,02 |
0,020… 0,025 |
|
Грунтовая дорога: сухая укатанная после дождя |
— |
0,025 …0,035 0,05…0,15 |
|
Песок |
— |
0,10…0,30 |
|
Укатанный снег |
— |
0,07…0,10 |
При движении автомобиля по дороге с твердым покрытием коэффициент f увеличивается по мере уменьшения давления рш воздуха в шине (рис. 3.3, б) за счет большей деформации шины.
При передаче увеличивающегося вращающего момента М коэффициент f немного возрастает (рис. 3.3, в), так как шина в этом случае деформируется не только в вертикальном (радиальном) направлении, но и по окружности (тангенциально).
При передаче большого вращающего момента элементы протектора проскальзывают по дороге, и на трение в области контакта затрачивается дополнительная энергия.
Качение колеса по мягкому грунту вызывает уплотнение частиц грунта под колесом и смещение их в сторону движения автомобиля. На коэффициент сопротивления качению при этом влияют глубина колеи, тип и состояние грунта, диаметр колеса и воспринимаемая им вертикальная нагрузка. Понижение давления воздуха в шине приводит к уменьшению глубины колеи, однако при этом возрастают внутренние потери в шине. Поэтому для каждой шины можно найти такое внутреннее давление воздуха, при котором на данном грунте коэффициент f имеет наименьшее значение.
Мощность1, необходимая для преодоления силы Рf сопротивления
качению машины, составит, Вт:

где G — вес машины, Н; u — скорость движения, м/с. 1 Единица измерения мощности — ватт (1 Вт = 1 Н*м/с).
Трение и сопротивление качению
Процесс трения (фрикционное взаимодействие) играет важную роль в промышленном мире и повседневной жизни. Сила трения оказывает сопротивление скольжению, вращению, качению, полёту объекта из-за его контакта с другим объектом. Она может быть полезной (к примеру, когда нужно задействовать тормоза, чтобы остановить автомобиль), или вредной (при попытке ехать с ногой на педали тормоза). Эта статья расскажет о важном аспекте промышленных колёс – о сопротивлении качению.
Сопротивление качению – притормаживающее действие, которое оказывает поверхность пола на шинку (контактный слой) катящегося колеса. Оно является мерой энергии, потерянной на определённом расстоянии.
Рассмотрим катящееся по плоской поверхности колесо. Его шинка деформируется, что вызывает некоторое сопротивление движению качения. Плоская поверхность также может деформироваться, особенно если она мягкая. Хорошие примеры сильно сопротивляющихся вращению поверхностей – грязь или песок. Катить тележку по асфальту значительно легче, чем по песку.
Факторы, влияющие на рассеивание энергии катящегося промышленного колеса:
- трение контактирующих поверхностей;
- упругие свойства материалов;
- грубость поверхностей.
Трение качения и трение скольжения
Коэффициент трения качения не следует путать с коэффициентом трения скольжения. Коэффициент трения скольжения выражает отношение силы трения между телами и силы, прижимающей тела друг к другу. Данный коэффициент зависит от типа используемых материалов. К примеру, сталь на льду имеет низкий коэффициент трения, а резина на асфальте имеет высокий коэффициент трения.
Рисунок 2 поясняет понятие трения скольжения. Представьте силу, которую нужно применить, чтобы протянуть тяжёлый ящик по полу. Статическое трение требует применения определённой силы, чтобы сдвинуть ящик с места. С началом движения, возникает динамическое трение, требующее постоянного приложения определенной силы для поддержания движения. В этом примере, человек, толкающий ящик, прикладывает силу Fapp, ящик весит N, а пол создает силу трения f, которая сопротивляется движению.
Причина, по которой мы используем колёса для перемещения материалов в том, что они позволяют тратить значительно меньше силы. Представьте, что приходится волочь холодильник или пианино! Более того, подумайте, насколько легче было бы передвинуть вышеупомянутый ящик, если бы применялись колёса.
Сила, требуемая для передвижения оборудования на колёсах, велика только при старте. Ее часто называют «первоначальной или «стартовой» силой. Как только получено нужное ускорение, для продолжения движения необходима гораздо меньшая сила, которую называют «перманентной» или «катящей». Как правило «стартовая» сила превышает ее в 2-2.5 раза.
Расчёт силы трения качения
Помочь узнать сопротивление качению промышленных колёс помогает коэффициент трения качения. Его значение для различных материалов получено эмпирическим путем и может варьироваться в зависимости от скорости вращения колеса, нагрузки на колесо, материала опорной поверхности.
В таблице ниже приведены коэффициенты трения качения наиболее распространенных материалов, из которых изготавливают промышленные колеса. Неудивительно, что самый мягкий, легко деформирующийся материал (резина) обладает самым высоким коэффициентом трения качения, а самый твёрдый материал (кованая сталь) – самым низким.
|
Материал шинки (контактного слоя колеса) |
Материал пола |
Коэффициент трения качения (масса груза – 600 кг, скорость – 5 км/ч) |
|
Кованая сталь |
сталь |
0.019 |
|
Чугун |
сталь |
0.021 |
|
Твёрдая резина |
сталь |
0.303 |
|
Полиуретан |
сталь |
0.03–0.057 |
|
Литой нейлон |
сталь |
0.027 |
|
Фенол |
сталь |
0.026 |
Формула для расчётов
F = f х F/R
F = сила трения качения
f = коэффициент трения качения
W = сила давления на опору (вес)
R = радиус колеса
Из формулы видно, что сила трения качения F пропорциональна силе давления на опору W и обратно пропорциональна радиусу R колеса. Таким образом, диаметр колес играет важную роль при транспортировке тяжёлых грузов.
Узнав силу трения качения каждого и умножив ее на число, можно узнать примерную силу сопротивления движению. Однако вышеприведенная формула неточна, потому что не учитывает другие факторы, влияющие на лёгкость качения (к примеру, силу адгезии).
Как выбрать промышленные колёса для лёгкого передвижения?
Чтобы снизить сопротивление качению, необходимо выбирать колёса большого диаметра и из материалов с низким коэффициентом трения.
Выбор подшипников не столь критичен для лёгкости хода тележки, как диаметр и материал шинки. Понятно, что подшипники качения предпочтительнее подшипников скольжения. Также стоит учитывать, что шариковые и роликовые подшипники лучше выдерживают нагрузки, меньше изнашиваются и дольше служат.
Главные факторы, влияющие на сопротивление качению:
- масса;
- диаметр колес;
- материал и мягкость шинки;
- материал и качество поверхности пола;
- условия на полу (грубость поверхности, чистота, наклон и т.д.).
Факторы, которые обычно игнорируют:
- тип подшипников;
- рисунок протектора;
- эффект скольжения или адгезии;
- температура окружающей среды;
- уклоны поверхности.
Общие рекомендации:
- Покупайте колесо промышленное, основываясь на грузоподъёмности и состоянии полов.
- Дополнительно принимайте во внимание: диапазон температур, ударопрочность, устойчивость к влаге, стойкость к свету и химикатам, возможность восстановления.
- Выбирайте максимально большой из возможных диаметров.
- Остановите выбор на шинке с минимальным сопротивлением качению.
- Подсчитайте силу сопротивления качению, принимая во внимание величину «стартовой» силы.
- Учитывайте фактор безопасности.
- Помните про уклоны поверхности. Сопротивление качению возрастает на подъёмах и снижается на спусках. F = Fx/cosa.
- Для буксировки самоходным транспортом лучше выбирать промышленные колёса с шариковыми подшипниками в оси. Только они обеспечат большой пробег, выдержат высокие скорости и нагрузки.
Легкой вам работы!





![{displaystyle C_{rr}=0.0048(18/D)^{frac {1}{2}}(100/W)^{frac {1}{4}}={frac {0.0643988}{sqrt[{4}]{WD^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcdf0492d842147e528ef3ff457a3c7fb80b175d)







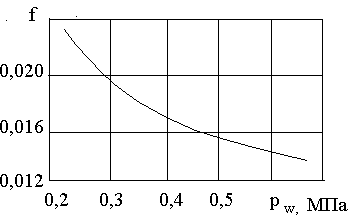
 на рисунке 1.),
на рисунке 1.),
 — глубина погружения
— глубина погружения — диаметр жесткого колеса
— диаметр жесткого колеса![{ displaystyle C_ {rr} = 0,0048 (18 / D) ^ { frac {1} {2}} (100 / Вт) ^ { frac {1} {4}} = { frac {0,0643988 } { sqrt [{4}] {WD ^ {2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96bcbd5d3df8882ad84fb89a7ab42d85d7de6513)
 — диаметр колеса в дюймах
— диаметр колеса в дюймах — нагрузка на колесо в фунтах-силах
— нагрузка на колесо в фунтах-силах
 — линейная скорость тела (на оси), а
— линейная скорость тела (на оси), а его скорость вращения.
его скорость вращения.


