- Главная
- Справочники
- Справочник по математике 5-9 класс
- Отношения и пропорции
- Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
Где 



Например:
14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
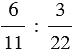
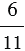
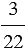
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел 





Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел 



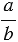
Основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Запишем отношение числа 3 к числу 10 и найдем его значение:
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Пример:
Сколько процентов составляет число 5 от числа 10?
51021·100%=12·100%=1002%=50%.
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
1 м = 100 см;
Отношение длины прямоугольника к его ширине равно 12 : 100 = 
Отношение ширины прямоугольника к его длине равно 100 : 12 = 
Дроби 

На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).
Например:
Пусть на карте задан масштаб 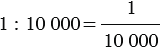
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через 

5 : 
Решаем данное уравнение:



50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через 


Решаем данное уравнение:


0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
Советуем посмотреть:
Пропорции
Прямая и обратная пропорциональные зависимости
Длина окружности и площадь круга
Отношения и пропорции
Правило встречается в следующих упражнениях:
6 класс
Номер 671,
Мерзляк, Полонский, Якир, Учебник
Номер 689,
Мерзляк, Полонский, Якир, Учебник
Номер 988,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Задание 734,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 736,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 761,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 809,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1581,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 146,
Мерзляк, Полонский, Якир, Учебник
Номер 150,
Мерзляк, Полонский, Якир, Учебник
Номер 198,
Мерзляк, Полонский, Якир, Учебник
Номер 230,
Мерзляк, Полонский, Якир, Учебник
Номер 405,
Мерзляк, Полонский, Якир, Учебник
Номер 406,
Мерзляк, Полонский, Якир, Учебник
Номер 426,
Мерзляк, Полонский, Якир, Учебник
Номер 846,
Мерзляк, Полонский, Якир, Учебник
Номер 847,
Мерзляк, Полонский, Якир, Учебник
Номер 943,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 303,
Мерзляк, Полонский, Якир, Учебник
Rectangles have four sides, and generally the adjacent sides are not equal. Knowing the measurements of the two sides allows you to create a ratio of the rectangle. This tells you how much bigger one side is compared to the other side. This is used in basic geometry and helps students understand properties of a rectangle. If you know the ratio of a rectangle and know the measurement of one side, you can calculate the adjacent side.
-
Rectangles with the same length-to-width ratios are considered similar.
Measure your rectangle’s sides. For example, assume your rectangle has a side of 8 inches and another of 4 inches.
Set up a ratio where your large side is on top of the fraction and the smaller side is on the bottom of the fraction. In the example, 8 inches / 4 inches.
Divide the ratio, then set the bottom number to one. In the example, 8 divided by 4 equals 2. So your ratio is 2 to 1.
Tips
Онлайн калькулятор для вычисления соотношение между сторонами, например для вычисления соотношения сторон экрана, фотографий, форматов бумаги и т.д.
Для вычисления применяем метод сокращения дробей.
Пример: Вычислить соотношение сторон формата а4, для этого достаточно ввести размеры в калькулятор ширину и высоту листа 29,7 х 21,0 сантиметров и получить ответ ответ 99 : 70.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также
Прямоугольники имеют четыре стороны, и, как правило, смежные стороны не равны. Знание измерений двух сторон позволяет создать соотношение прямоугольника. Это говорит вам, насколько больше одна сторона по сравнению с другой стороной. Это используется в базовой геометрии и помогает студентам понять свойства прямоугольника. Если вы знаете соотношение прямоугольников и знаете размеры одной стороны, вы можете рассчитать соседнюю сторону.
-
Прямоугольники с одинаковым отношением длины к ширине считаются одинаковыми.
Измерьте стороны вашего прямоугольника. Например, предположим, что у вашего прямоугольника есть сторона 8 дюймов, а другая — 4 дюйма.
Установите соотношение, где ваша большая сторона находится сверху фракции, а меньшая — снизу фракции. В примере 8 дюймов / 4 дюйма.
Разделите соотношение, затем установите нижнее число на единицу. В этом примере 8, деленное на 4, равно 2. Таким образом, ваше соотношение составляет 2 к 1.
подсказки
Содержание
- 51. Планиметрия Читать 0 мин.
- 51.506. Отношения
- Что значит отношение длины
- Сравнение отрезков. Действия над отрезками.
- Равные и неравные отрезки
- Свойство отрезков, отсекаемых параллельными прямыми на сторонах угла
- Пропорциональные отрезки
- Построение пропорциональных отрезков
- Отношения
- Основное свойство отношения:
51. Планиметрия  Читать 0 мин.
Читать 0 мин.
51.506. Отношения
Зачастую в геометрических задачах в условии даются отношения отрезков и площадей или отношение отрезков нужно найти. Существует ряд теорем и свойств фигур и их элементов, в которых так или иначе используются отношения.
ОТНОШЕНИЯ ОТРЕЗКОВ:
1. Все медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 к 1, считая от вершины: AO : AM = 2 : 1.
2. Средняя линия треугольника равна половине основания: $MN = frac<1><2>BC$
3. Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна ее половине $CM = frac<1><2>AB$
4. Диагонали параллелограмма точкой пересечения делятся пополам.
Произвольный параллелограмм или ромб:
Прямоугольник или квадрат:
ОТНОШЕНИЯ ПЛОЩАДЕЙ:
1. Медиана разбивает треугольник на два равновеликих (по площади) треугольника: $S_ = S_ = S$
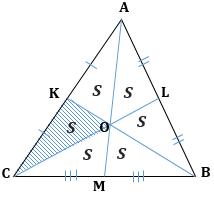
2. Треугольник делится тремя медианами на шесть равновеликих треугольников:
3. Если площадь треугольника равна S, то площадь треугольника, составленного из его медиан, равна $frac<3><4>S$
ЛЕММЫ О ПЛОЩАДЯХ ТРЕУГОЛЬНИКА:
Площади подобных фигур относятся как квадрат коэффициента подобия.
Если стороны треугольников с общей вершиной лежат на одной прямой, то их площади относятся как основания.
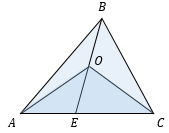
Если два треугольника имеют общую сторону, то их площади соотносятся как длины отрезков BE и OE.
Если два треугольника имеют общий угол, то их площади соотносятся как произведения соответствующих сторон, прилежащих к этому углу.
Лемма 4 применима даже в том случае, если точки нового треугольника были взяты не на сторонах, а на продолжениях сторон. Пусть точка Е лежит на продолжении стороны AB за вершину В.
Источник
Что значит отношение длины
ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ. ПОДОБИЕ ФИГУР.
§ 82. ОТНОШЕНИЕ ОТРЕЗКОВ.
Отношением двух отрезков называется отношение тех чисел, которые выражают длины этих отрезков при условии, что отрезки измерены единицами одного наименования.
В арифметике отношением одного числа к другому называется частное от деления первого числа на второе, поэтому можно сказать, что отношением одного отрезка к другому является частное от деления длины первого отрезка на длину второго, если длины отрезков выражены в единицах одного наименования.
Отношение одного отрезка к другому обычно изображается в виде частного (дроби): AB /CD.
Если даны два отрезка АВ = 6 см и СD = 4 см, то отношение отрезка АВ к отрезку СD равно 6 /4, т. е.
В этом случае делимое (АВ) называется предыдущим членом отношения,
делитель (СD) — последующим членом отношения, а частное (1,5) — отношением.
Отношение отрезка СD к отрезку АВ равно 4 /6, т. е.
Это отношение в десятичных дробях придётся выражать приближённо: CD /AB ≈ 0,67
(с точностью до 0,01 с избытком), так как CD /AB =0,6666. .
Если длины отрезков выражены приближённо, то отношение тоже получится приближённым.
Пусть АВ ≈ 6,5 см, СD ≈ 2,7 см, тогда AB /CD ≈ 6,5 /2,7 , AB /CD ≈ 2,4 (с точностью до 0,1 с недостатком).
2. Независимость отношения от принятой единицы измерения.
Пусть мы имеем два отрезка, длины которых выражены в метрах. Например: АВ = 6 м, ОС = 2 м. Найдём их отношение:
Изменится ли величина отношения, если мы длины этих отрезков выразим в других мерах, например в сантиметрах? Тогда АВ = 600 см, ОС = 200 см. Найдём их отношение:
Отношение отрезков в том и другом случае не изменилось, так как для выражения длин отрезков в сантиметрах мы оба члена отношения АВ и ОС умножили на одно и то же число (на 100). Значит, отношение отрезков не зависит от выбора единиц измерения.
Необходимо лишь, чтобы длины обоих отрезков были выражены мерами одного и того же наименования.
1. Найти отношение отрезков AВ и СD при условии, если:
а) АВ = 12см, СD = 3 см;
б) АВ = 2 м; СD = 80 см.
2. Найти отношение отрезков АВ и СD с точностью до 0,1 и 0,01 при условии, если:
а) АВ = 7 см, СD = 3 см;
б) АВ = 13 см, СD = 7 см.
Источник
Сравнение отрезков. Действия над отрезками.
Равные и неравные отрезки
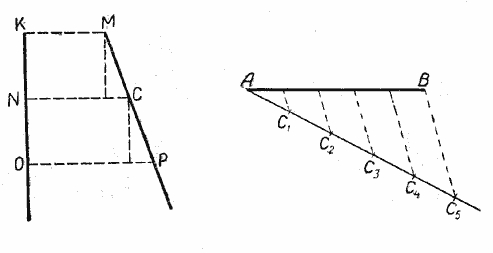
Пусть нам даны два отрезка АВ и СD (рис.). Наложим отрезок АВ на отрезок CD так, чтобы точка А совпала с точкой С, и отрезок АВ направим по отрезку CD. Если точка В совпадаете точкой D, то отрезки АВ и CD равны; АВ = CD.
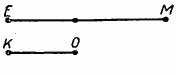
Сравним два отрезка КО и ЕМ (рис.).
Наложим отрезок КО на отрезок ЕМ так, чтобы точки К и Е совпали. Отрезок КО направим по отрезку ЕМ. Если точка О окажется где-нибудь между точками Е и М, то говорят, что отрезок ЕМ больше отрезка КО; отрезок КО меньше отрезка ЕМ.
Записывается это тaк: ЕМ > КО, КО 1 /5 часть отрезка МN.
в) Чтобы разделить отрезок на равные части с помощью циркуля, поступают таким образом. Например, если нужно разделить отрезок на две равные части, то циркуль раздвигают на глаз так, чтобы раствор циркуля составлял примерно половину отрезка. Затем на данном отрезке от его конца последовательно один за другим откладывают этим раствором циркуля два отрезка. Если полученная сумма отрезков будет меньше данного отрезка, тo раствор циркуля увеличивают; если сумма окажется больше данного отрезка, то раствор циркуля уменьшают. Так, постепенно исправляя ошибку, можно отыскать довольно точнo половину отрезка (рис.).
Таким же образом выполняется приближённое деление отрезка на 3, 4, 5 и т. д. равных частей. Только в этом случае надо брать на глаз 1 /3; 1 /4; 1 /5 . отрезка и откладывать взятый отрезок 3, 4, 5. раз, смотря по тому, на сколько равных частей надо разделить данный отрезок.
Свойство отрезков, отсекаемых параллельными прямыми на сторонах угла
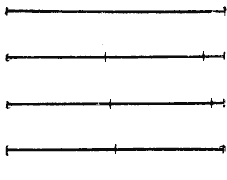
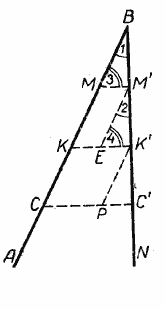
Пусть на стороне АВ угла АВN отложены равные отрезки ВМ = МК = КС (рис.) и через точки деления М, К и С проведены параллельные прямые, пересекающие сторону ВN того же угла.
На этой стороне образовались три отрезка: ВМ’, М’К’ и К’С’. Требуется доказать, что ВМ’ = М’К’ = К’С’.
Для доказательства через точки М’ и К’ проведём прямые, параллельные АВ. Мы получим треугольники ВММ’, М’ЕК’ и К’РС’. Сравним эти треугольники.
Сначала сравним треугольники МВМ’ и М’ЕК’. В этих треугольниках имеем:
∠1 = ∠2, как соответственные углы при параллельных ВА и М’Е и секущей ВN;
∠3 = ∠4, как острые углы 1 с соответственно параллельными сторонами (АВ || М’Е и ММ’ || КК’).
ВМ = МК по построению;
МК = М’Е, как противоположные стороны параллелограмма.
Углы 1-й и 4-й могут оказаться оба тупыми, но и в этом случае они останутся равными, а потому доказательство теоремы не изменится.
Следовательно, ВМ = М’Е. Таким образом, ΔВММ’ = ΔМ’ЕК’ (по стороне и двум прилежащим к ней углам). Отсюда следует, что ВМ’ = М’К’.
Так же можно доказать, что ВМ’ = К’С’, т. е. ВМ’ = М’К’ = К’С’. При доказательстве теоремы мы откладывание отрезков начали от вершины угла, но теорема справедлива и для того случая, когда откладывание отрезков будет начато не от вершины угла, а от любой точки его стороны.
В этом случае вершину угла на чертеже можно не отмечать (рис.).
Теорема справедлива и для случая, когда прямые КО и МР параллельны.
Пропорциональные отрезки
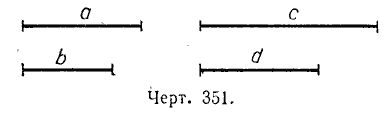
Из арифметики известно, что равенство двух отношений называется пропорцией. Например: 16 /4 = 20 /5; 2 /3 = 4 /6 To же самое имеем и в геометрии: если даны две пары отрезков, отношения которых равны, то можно составить пропорцию.
отрезки а, b, c, d называются пропорциональными.
Отношение a /b называется, как и в арифметике, первым отношением, c /d — вторым отношением; а и d называются крайними членами пропорции, b и с — средними членами.
В пропорции можно поменять местами отношения; можно переставить крайние члены, средние члены; можно переставить те и другие одновременно.
Поскольку в пропорции a /b = c /d под буквами подразумевают числа, выражающие длины отрезков, то произведение крайних членов её равно произведению средних членов. Отсюда, зная три члена пропорции, можно найти неизвестный четвёртый её член. Так, в пропорции a /x = c /d x = a • d /c
Отметим ещё некоторые свойства пропорций, которыми придётся в дальнейшем пользоваться при доказательстве некоторых теорем и при решении задач.
а) Если три члена одной пропорции соответственно равны трём членам другой пропорции, то равны и четвёртые члены этих пропорций.
б) Если в пропорции равны предыдущие члены, то равны и последующие, т. е. если a /x = a /y , то х = у.
Чтобы убедиться в этом, переставим средние члены в этой пропорции.
А это возможно лишь в том случае, когда числитель и знаменатель дроби равны, т. е.
в) Если в пропорции равны последующие члены, то равны и предыдущие, т. е. если x /a = y /a , то х = у.
В справедливости этого свойства предлагается вам убедиться самостоятельно. Для этого проведите рассуждение, аналогичное предыдущему.
Построение пропорциональных отрезков
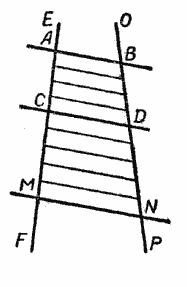
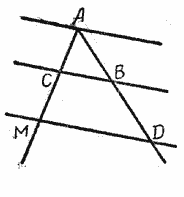
Пусть две прямые ЕF и ОР пересечены тремя параллельными прямыми АВ, СD и МN (рис.).
Требуется доказать, что отрезки АС, СМ, ВD и DN, заключённые между параллельными секущими, пропорциональны, т. е.
Пусть длина отрезка АС равна р, а длина отрезка СМ равна q.
Например, р = 4 см. и q = 5 см.
Разделим АС и СМ на отрезки, равные 1 см, и из точек деления проведём прямые, параллельные прямым АВ, СD и МN, как это показано на рисунке.
Тогда на прямой ОР отложатся равные между собой отрезки, при этом на отрезке BD их будет 4, а на отрезке DN — 5.
Отношение АС к СМ равно 4 /5 , точно так же и отношение ВD к DN равно 4 /5.
Значит, отрезки АС, СМ, ВD и DN пропорциональны. Пропорциональны также и отрезки АС, АМ, ВD и ВN (налегающие друг на друга), т. е. AC /AM = BD /BN,
Теорема будет справедлива и при любых других целых значениях р и q.
Если длины отрезков АС и СМ не выразятся в целых числах при данной единице измерения (например, сантиметре), то надо взять такую более мелкую единицу (например, миллиметр или микрон), при которой длины отрезков АС и СМ практически выразятся в целых числах.
Доказанная теорема справедлива и в том случае, когда одна из параллельных секущих проходит через точку пересечения данных прямых. Она справедлива также и в том случае, когда отрезки откладываются не непосредственно один за другим, а через некоторый промежуток.
Источник
Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
Где 



14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
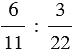
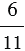
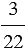
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел 





Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел 



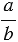
Основное свойство отношения:
Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Запишем отношение числа 3 к числу 10 и найдем его значение:
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах.
Процентное отношение показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Пример:
Сколько процентов составляет число 5 от числа 10?
5 10 2 1 · 100 % = 1 2 · 100 % = 100 2 % = 50 % .
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
Отношение длины прямоугольника к его ширине равно 12 : 100 = 
Отношение ширины прямоугольника к его длине равно 100 : 12 = 
Дроби 

На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана).
Пусть на карте задан масштаб 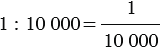
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через 

5 : 
Решаем данное уравнение:



50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через 


Решаем данное уравнение:


0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
Поделись с друзьями в социальных сетях:
Источник

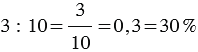
 Читать 0 мин.
Читать 0 мин.