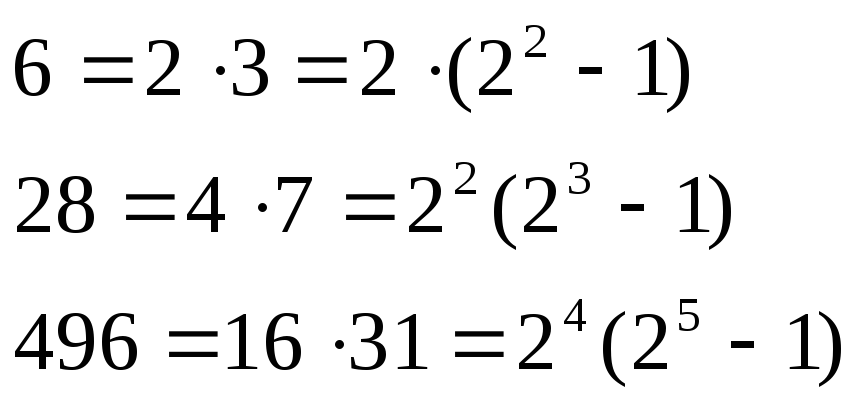Примеры собственного делителя числа
Пример собственного делителя числа:
Число 4 имеет собственные делители 1 и 2
Ещё пример собственного делителя числа:
Число 14 имеет собственные делители 1, 2, 7
Другой пример собственного делителя числа:
Число 12 имеет собственные делители 1, 2, 3, 4 и 6
Собственный делитель простых чисел
У любого простого числа имеется только один собственный делитель – это единица.
Пример.
Простое число 5 имеет делители 1 и 5, из них, в соответствии с определением собственного делителя, только 1 есть собственный делитель.
Собственный делитель составных чисел
У любого составного числа имеется более одного собственного делителя.
Пример.
Простое число 15 имеет делители 1, 3, 5 и 15, из них, в соответствии с определением собственного делителя, 1, 3 и 5 есть собственные делители.
Собственный делитель натурального числа — это любой делитель, кроме самого этого числа. Если число равно сумме своих собственных делителей, то оно называется совершенным. Так, 6 = 3 + 2 + 1 — это наименьшее из всех совершенных чисел (1 не в счет), 28 = 14 + 7 + 4 + 2 + 1 — это еще одно такое число.
Совершенные числа были известны еще в древности и интересовали ученых во все времена. В «Началах» Евклида доказано, что если простое число имеет вид 2n – 1 (такие числа называют простыми числами Мерсенна), то число 2n–1(2n – 1) — совершенное. А в XVIII веке Леонард Эйлер доказал, что любое четное совершенное число имеет такой вид.
Задача
Попробуйте доказать эти факты и найти еще пару-тройку совершенных чисел.
Подсказка 1
а) Чтобы доказать утверждение из «Начал» (что если простое число имеет вид 2n – 1, то число 2n–1(2n – 1) — совершенное), удобно рассмотреть сигма-функцию, которая равна сумме всех положительных делителей натурального числа n. Например, σ(3) = 1 + 3 = 4, а σ(4) = 1 + 2 + 4 = 7. Эта функция обладает полезным свойством: она мультипликативна, то есть σ(ab) = σ(a)σ(b); равенство выполняется для любых двух взаимно простых натуральных чисел a и b (взаимно простыми называются числа, у которых нет общих делителей). Это свойство можно попытаться доказать или принять на веру.
При помощи сигма-функции доказательство совершенности числа N = 2n–1(2n – 1) сводится к проверке того, что σ(N) = 2N. Для этого пригодится мультипликативность этой функции.
б) Другой путь решения не использует никаких дополнительных конструкций вроде сигма-функции. Он опирается только на определение совершенного числа: нужно выписать все делители числа 2n–1(2n – 1) и найти их сумму. Должно получиться это же число.
Подсказка 2
Доказывать, что любое четное совершенное число — это степень двойки, умноженная на простое число Мерсенна, также удобно с помощью сигма-функции. Пусть N — какое-нибудь четное совершенное число. Тогда σ(N) = 2N. Представим N в виде N = 2k·m, где m — нечетное число. Поэтому σ(N) = σ(2k·m) = σ(2k)σ(m) = (1 + 2 + … + 2k)σ(m) = (2k+1 – 1)σ(m).
Получается, что 2·2k·m = (2k+1 – 1)σ(m). Значит, 2k+1 – 1 делит произведение 2k+1·m, а поскольку 2k+1 – 1 и 2k+1 взаимно просты, то m должно делиться на 2k+1 – 1. То есть m можно записать в виде m = (2k+1 – 1)·M. Подставив это выражение в предыдущее равенство и сократив на 2k+1 – 1, получим 2k+1·M = σ(m). Теперь до окончания доказательства остается всего один, хотя и не самый очевидный, шаг.
Решение
В подсказках содержится значительная часть доказательств обоих фактов. Восполним здесь недостающие шаги.
1. Теорема Евклида.
а) Для начала нужно доказать, что сигма-функция действительно мультипликативна. На самом деле, поскольку каждое натуральное число однозначно раскладывается на простые множители (это утверждение называют основной теоремой арифметики), достаточно доказать, что σ(pq) = σ(p)σ(q), где p и q — различные простые числа. Но довольно очевидно, что в этом случае σ(p) = 1 + p, σ(q) = 1 + q, а σ(pq) = 1 + p + q + pq = (1 + p)(1 + q).
Теперь завершим доказательство первого факта: если простое число имеет вид 2n – 1, то число N = 2n–1(2n – 1) — совершенное. Для этого достаточно проверить, что σ(N) = 2N (так как сигма-функция — это сумма всех делителей числа, то есть сумма собственных делителей плюс само число). Проверяем: σ(N) = σ(2n–1(2n – 1)) = σ(2n–1)σ(2n – 1) = (1 + 2 + … + 2n–1)·((2n – 1) + 1) = (2n – 1)·2n = 2N. Здесь было использовано, что раз 2n – 1 — простое число, то σ(2n – 1) = (2n – 1) + 1 = 2n.
б) Доведем до конца и второе решение. Найдем все собственные делители числа 2n–1(2n – 1). Это 1; степени двойки 2, 22, …, 2n–1; простое число p = 2n – 1; а также делители вида 2m·p, где 1 ≤ m ≤ n – 2. Суммирование всех делителей тем самым разбивается на подсчет сумм двух геометрических прогрессий. Первая начинается с 1, а вторая — с числа p; у обеих знаменатель равен 2. По формуле суммы элементов геометрической прогрессии сумма всех элементов первой прогрессии равна 1 + 2 + … + 2n–1 = (2n – 1)/2 – 1 = 2n – 1 (и это равно p). Вторая прогрессия дает p·(2n–1 – 1)/(2 – 1) = p·(2n–1 – 1). Итого, получается p + p·(2n–1 – 1) = 2n–1·p — то, что надо.
Скорее всего, Евклид не был знаком с сигма-функцией (да и вообще с понятием функции), поэтому его доказательство изложено несколько другим языком и ближе к решению из пункта б). Оно содержится в предложении 36 из IX книги «Начал» и доступно, например, здесь.
2. Теорема Эйлера.
Прежде чем доказывать теорему Эйлера, отметим еще, что если 2n – 1 — простое число Мерсенна, то n также должно быть простым числом. Дело в том, что если n = km — составное, то 2km – 1 = (2k)m – 1 делится на 2k – 1 (поскольку выражение xm – 1 делится на x – 1, это одна из формул сокращенного умножения). А это противоречит простоте числа 2n – 1. Обратное утверждение — «если n — простое, то 2n – 1 также простое» — не верно: 211 – 1 = 23·89.
Вернемся к теореме Эйлера. Наша цель — доказать, что любое четное совершенное число имеет вид, полученный еще Евклидом. В подсказке 2 были намечены первые этапы доказательства, и осталось сделать решающий шаг. Из равенства 2k+1·M = σ(m) следует, что m делится на M. Но m делится также и на само себя. При этом M + m = M + (2k+1 – 1)·M = 2k+1·M = σ(m). Это означает, что у числа m нет других делителей, кроме M и m. Значит, M = 1, а m — простое число, которое имеет вид 2k+1 – 1. Тогда N = 2k·m = 2k(2k+1 – 1), что и требовалось.
Итак, формулы доказаны. Применим их, чтобы найти какие-нибудь совершенные числа. При n = 2 формула дает 6, а при n = 3 получается 28; это первые два совершенных числа. По свойству простых чисел Мерсенна, нам нужно подобрать такое простое n, что 2n – 1 будет также простым числом, а составные n можно вообще не рассматривать. При n = 5 получится 2n – 1 = 32 – 1 = 31, это нам подходит. Вот и третье совершенное число — 16·31 = 496. На всякий случай проверим его совершенность явно. Выпишем все собственные делители 496: 1, 2, 4, 8, 16, 31, 62, 124, 248. Их сумма равна 496, так что всё в порядке. Следующее совершенное число получается при n = 7, это 8128. Соответствующее простое число Мерсенна равно 27 – 1 = 127, и довольно легко проверить, что оно действительно простое. А вот пятое совершенное число получается при n = 13 и равно 33 550 336. Но проверять его вручную уже очень утомительно (однако это не помешало кому-то открыть его еще в XV веке!).
Послесловие
Первые два совершенных числа — 6 и 28 — были известны с незапамятных времен. Евклид (и мы вслед за ним), применив доказанную нами формулу из «Начал», нашел третье и четвертое совершенные числа — 496 и 8128. То есть сначала было известно всего два, а потом четыре числа с красивым свойством «быть равными сумме своих делителей». Больше таких чисел обнаружить не могли, да и эти, на первый взгляд, ничего не объединяло. В эпоху древности люди были склонны вкладывать мистический смысл в таинственные и непонятные явления, поэтому и совершенные числа получили особый статус. Пифагорейцы, оказавшие сильное влияние на развитие науки и культуры того времени, также поспособствовали этому. «Всё есть число», — говорили они; число 6 в их учении обладало особыми магическими свойствами. А ранние толкователи Библии объясняли, что мир был сотворен именно на шестой день, потому что число 6 — самое совершенное среди чисел, ибо оно первое среди них. Также многим казалось неслучайным, что Луна делает оборот вокруг Земли примерно за 28 дней.
Пятое совершенное число — 33 550 336 — было найдено только в XV веке. Еще почти через полтора века итальянец Катальди нашел шестое и седьмое совершенные числа: 8 589 869 056 и 137 438 691 328. Им соответствуют n = 17 и n = 19 в формуле Евклида. Обратите внимание, что счет идет уже на миллиарды, и страшно даже представить, что все вычисления были проделаны без калькуляторов и компьютеров!
Как мы знаем, Леонард Эйлер доказал, что любое четное совершенное число должно иметь вид 2n–1(2n – 1), причем 2n – 1 должно быть простым. Восьмое число — 2 305 843 008 139 952 128 — нашел тоже Эйлер в 1772 году. Здесь n = 31. После его достижений можно было осторожно сказать, что про четные совершенные числа науке стало что-то понятно. Да, они быстро растут, и их трудно вычислять, но хотя бы ясно, как это делать: надо брать числа Мерсенна 2n – 1 и искать среди них простые. Про нечетные совершенные числа неизвестно почти ничего. На сегодняшний день не найдено ни одного такого числа, при том что проверены все числа до 10300 (видимо, нижняя граница отодвинута даже дальше, просто соответствующие результаты еще не опубликованы). Для сравнения: число атомов в видимой части Вселенной оценивается величиной порядка 1080. При этом не доказано, что нечетных совершенных чисел не существует, просто это может быть очень большое число. Даже настолько большое, что наши вычислительные мощности никогда до него не доберутся. Существует ли такое число или нет — одна из открытых на сегодня проблем математики. Компьютерным поиском нечетных совершенных чисел занимаются участники проекта OddPerfect.org.
Вернемся к четным совершенным числам. Девятое число было найдено в 1883 году сельским священником из Пермcкой губернии И. М. Первушиным. В этом числе 37 цифр. Таким образом, к началу XX века было найдено всего 9 совершенных чисел. В это время появились механические арифметические машины, а в середине века — и первые компьютеры. С их помощью дело пошло быстрее. Сейчас найдено 47 совершенных чисел. Причем только у первых сорока известны порядковые номера. Еще про семь чисел пока точно не установлено, какие они по счету. В основном поиском новых мерсенновских простых (а с ними — и новых совершенных чисел) занимаются участники проекта GIMPS (mersenne.org).
В 2008 году участниками проекта было найдено первое простое число, в котором больше 10 000 000 = 107 цифр. За это они получили приз $100 000. Денежные призы 150 000 и 250 000 долларов также обещаны за простые числа, состоящие из больше чем 108 и 109 цифр соответственно. Предполагается, что из этих денег получат вознаграждение и те, кто нашел меньшие, но еще не открытые простые числа Мерсенна. Правда, на современных компьютерах проверка чисел такой длины на простоту займет годы, и это, наверное, дело будущего. Самое большое простое число на сегодня равно 243112609 – 1. Оно состоит из 12 978 189 цифр. Отметим, что благодаря тесту Люка—Лемера (см. его доказательство: A proof of the Lucas–Lehmer Test) сильно упрощается проверка на простоту чисел Мерсенна: не нужно пытаться найти хотя бы один делитель очередного кандидата (это очень трудоемкая работа, которая для таких больших чисел практически невыполнима сейчас).
У совершенных чисел есть забавные арифметические свойства:
- Каждое четное совершенное число является также треугольным числом, то есть представимо в виде 1 + 2 + … + k = k(k + 1)/2 для некоторого k.
- Каждое четное совершенное число, кроме 6, является суммой кубов последовательных нечетных натуральных чисел. Например, 28 = 13 + 33, а 496 = 13 + 33 + 53 + 73.
- В двоичной системе счисления совершенное число 2n–1(2n – 1) записывается очень просто: сначала идут n единиц, а потом — n – 1 нулей (это следует из формулы Евклида). Например, 610 = 1102, 2810 = 111002, 3355033610 = 11111111111110000000000002.
- Сумма чисел, обратных всем делителям совершенного числа (само число здесь тоже участвует), равна 2. Например, 1/1 + 1/2 + 1/4 + 1/7 + 1/14 + 1/28 = 2.
Ослабим требования к функции f(x).
Пусть среди её значений будут как
простые, так и составные, но простых
значений будет бесконечно много.
Например, среди чисел вида
нередко встречаются простые числа:
2,5,17,37,101,197,257,…
Но гипотеза о том, что их бесконечно
много это одна из нерешенных проблем.
Очень мало известно о представлении
простых чисел другими функциями.
Наверняка установлено лишь то, что среди
арифметических прогрессий a+bx
с взаимно простыми a
и b содержится
бесконечно много простых чисел (теорема
Дирихле, 1837).
Ситуация меняется, если воспользоваться
функциями нескольких переменных. Дирихле
доказал, что любая квадратичная форма
,
в которой коэффициенты
a, b,
c взаимно просты
генерирует бесконечное множество
простых чисел. Более того, из результатов
Матиясевича (о том, что диофантовесть
множества равносильна его перечислимости)
следует существование многочлена,
множество положительных значений
которого совпадает с множеством простых
чисел. Пример такого многочлена 6ой
степени от 26 переменных можно найти в
[-].
п.4 Основная теорема арифметики
Легко доказать, что любое натурально
число раскладывается на простые
множители, например,
.
Нельзя ли получить тот же результат,
перемножая другие простые числа? Докажем,
что это невозможно. Например, в равенстве
Совсем неочевидно, что сомножители
являются составными числами, тем не
менее, этот факт вытекает из следующей
теоремы.
Теорема: (Основная теорема арифметики)
Любое натуральное число
либо
является простым, либо его можно записать
в виде произведения простых чисел
причем единственным образом, с точностью
до порядка сомножителей.
Замечание:
и
считаются одним и тем же разложением
числа 30.
Доказательство: 1) Существование
разложения на множители.
Пусть
—
наименьший простой делитель a.
Тогда
.
Если
и
—
наименьший простой делитель
,
то
и, значит,
.
Аналогично получим
и так далее. Поскольку
через конечное число шагов получим
и
.
2) Единственность разложения.
Предположим, что а можно разложить
на множители двумя способами:
a делится на
делится на
.
Тогда (§2 п.1 свойство 4 + замечание) один
из множителей, например
делится на
.
Но
простое
.
Сократим равенство на
:
и повторим рассуждение. Получим
и так далее.
Если
,
то, сократив все одинаковые множители,
получим противоречивое равенство
.
Итак, произведения состоят из одинакового
числа равных сомножителей, т.е. разложение
а единственно.
■
Простые множители в разложении числа
а могут повторяться. Пусть множитель
встречаются
раз. Запишем такие произведения в виде
степеней и расположим все
по возрастанию.
Определение:
,
(*)
(*) — каноническое разложение числа а
на множители.
Пример:
Замечание 1: Сравним формулу
(*) с разложением вектора
по
базису:
.
Простые числа образуют мультипликативный
базис во множестве N
(—
коэффициенты разложения), чем объясняется
их особая роль при изучении свойств
натурального ряда.
Замечание 2: Число 1 не относится
к простым прежде всего потому, что иначе
нарушится единственность разложения
на множители ()
Замечание 3: Рациональные дроби
тоже однозначно записываются в
каноническом виде, если допустить
отрицательные значения
.
Например,
.
Следствие 1: Если
,
то любой делитель а имеет вид
,
где
( i = 1,…k)
Доказательство: Очевидно, любое
число d указанного
вида делит а. Обратно, пусть
.
Тогда
.
Следовательно все простые делители
числа d входят в
разложение а со степенями
.
■
Следствие 2: Пусть
,
.
Здесь
— простые числа, которые входят в
разложение хотя бы одного из чисел a
и b. Некоторые
из показателей
и
могут быть равны нулю. Пусть
,
.
Тогда
,
.
Доказательство: Пусть
.
Очевидно,
и
.
Пусть
— другой общий делитель a
и b. По следствию
1
,
где
и
.
Отсюда следует, что
.
Для НОК доказательство аналогично.
■
Пример: Найти НОД и НОК чисел
а = 1008 и b=1080
Имеем
.
Тогда
.
Замечание: Из следствия 2 сразу
же выводится формула
.
При всей кажущейся очевидности основной
теоремы арифметики ее нельзя произвольно
переносить на другие числовые системы.
Пример: Коротка арифметика Гильберта
— множества вида
:
=
{1,5,9,13,17,21,…}
с одной операцией умножения, относительно
которой множество
замкнуто
.
Числа
являются
составными, а, например, 9 или 21 — простыми
в
.
В этой арифметике число 693 раскладываются
на простые множители неоднозначно:
п5. Число делителей и сумма делителей
Основная теорема арифметики позволяет
дать ответ на некоторые вопросы о
натуральном числе а. Так, следствие
1 указывает, какие числа является
делителями а. Нетрудно подсчитать
сколько всего делителей имеет натуральное
число а, а также найти их сумму.
Обозначение:
— число всех делителей а.
—
сумма всех делителей числа а.
В дальнейшем будем использовать
обозначение
означающее,
что суммирование идет по всем делителям
а. Например,
.
Пример 1: Делители числа 18 это
1,2,3,6,9,18. Поэтому
Пример 2: Пусть р — простое число.
Тогда
.
Теорема 1: Пусть
Тогда
Доказательство: По следствию 1 п.4
любой делитель а имеет вид
,
где
.
Показатель
можно выбирать
способом, а именно, 0,1,2,….
Показатель
можно выбирать
способом и т.д. Значит, общее число
способом составить комбинацию
равно произведению
,
а так как различным комбинациям
соответствуют различные делители а,
то
.
■
Пример: Найти количество делителей
числа а = 360.
Имеем
.
Замечание: С геометрической
точки зрения величина
есть
число точек с целыми координатами,
лежащих на графике гиперболы
координатной четверти.
Теорема 2: Пусть
.
Тогда
Доказательство: Рассмотрим выражение
Чтобы
вычислить S раскроем
скобки, перемножая по одному слагаемому
из каждой скобки. Каждое такое произведение
есть делитель а, поэтому S
есть сумма всех делителей а, т.е.
С другой стороны, каждая из k
скобок содержит геометрическую
прогрессию со знаменателем
.
Применяя формулу суммы первых
членов прогрессии, получим требуемое.
■
Пример: Найти сумму делителей числа
а =360.
Имеем
В древнегреческой математике большой
интерес вызывали числа, равные сумме
своих собственных делителей (т.е. всех
делителей числа а, кроме самого а).
Пифагорейцы называли такие числа
совершенными, приписывая им мистические
свойства.
Определение: Число а
называется совершенным, если
т.е. если
Первые два совершенных числа это
6 = 1+2+3 и 28 = 1+2+4+7+14.
В древней Греции были еще известны
совершенные числа 496 и 8128.
Евклид вывел формулу, позволяющую
находить совершеннее числа, заметив
закономерность:
Теорема: (Евклид)
Пусть
,
причем
— простое число.
Тогда а — совершенное число.
Доказательство:
Обозначим
,
тогда
и по теореме 2
■
Замечание: Доказанная формула
означает, что каждое простое число
Мерсенна порождает совершенное число.
Эйлер доказал, что этой формулой
исчерпывается все множество четных
чисел. Существуют ли нечетные совершенные
числа, неизвестно.
Теорема: (Эйлер)
Пусть а — четное совершенное число.
Тогда а можно представить в виде
,
где
— простое число.
Доказательство: Число а —
четное, значит его можно записать в виде
,
где b — нечетное,
.
Из теоремы 2 следует, что
.
С другой стороны, а — совершенное
число, значит
.
Итак,
.
Числа
и
взаимно просты
b делится на
,
т.е.
,
где с — собственный делитель b.
Подставим это выражение в предыдущее
равенство.
Получим
.
Если
,
то число b имеет
различные делители 1, с, b,
значит,
.
Противоречие означает, что
,
а так как
,
то
— простое число.
■
Помимо совершенных чисел, в древности
выделяли так называемые дружественные
числа.
Определение: Числа а и b
называются дружественными, если
и
,
т.е сумма собственных делителей одного
из чисел равна другому числу.
Из определения следует, что
.
Совершенное число является дружественными
самому себе.
Пара дружественных чисел а = 220, b
= 284, была единственной, известной в
Древней Греции.
Среди натуральных чисел < 1000000 найдено
42 пары дружественных чисел. Общий метод
построения пар дружественных чисел
неизвестен.
Соседние файлы в предмете Математический анализ
- #
18.09.201812.74 Кб0Bilet_15.odt
- #
18.09.201818.34 Кб0Bilet_17.odt
- #
18.09.201828.15 Кб0Bilet_19.odt
- #
18.09.201822.26 Кб0Bilet_20.odt
- #
- #
- #
- #
- #
- #
- #
Содержание материала
- Как определить количество делителей конкретного числа
- Видео
- Признаки делимости чисел
- Определение [ править
- Как найти число простых делителей числа
- Простые и составные числа
- Чем отличаются друг от друга, как найти
- Тест Миллера Рабина
Как определить количество делителей конкретного числа
Чтобы узнать, сколько положительных делителей у конкретного числа a, каноническое разложение которого выглядит как a = p 1 s 1 · p 2 s 2 · … · p n s n , нужно найти значение выражения ( s 1 + 1 ) · ( s 2 + 1 ) · … · ( s n + 1 ) . О количестве наборов переменных t 1 , t 2 , … , t n мы можем судить по величине записанного выражения.
Покажем на примере, как это вычисляется. Определим, сколько будет натуральных делителей у числа 3 900 , которое мы использовали в предыдущей задаче. Каноническое разложение мы уже записывали: 3 900 = 2 2 · 3 · 5 2 · 13 . Значит, s 1 = 2 , s 2 = 1 , s 3 = 2 , s 4 = 1 . Теперь подставим значения s 1 , s 2 , s 3 и s 4 в выражение ( s 1 + 1 ) · ( s 2 + 1 ) · ( s 3 + 1 ) · ( s 4 + 1 ) и вычислим его значение. Имеем ( 2 + 1 ) · ( 1 + 1 ) · ( 2 + 1 ) · ( 1 + 1 ) = 3 · 2 · 3 · 2 = 36 . Значит, это число имеет всего 36 делителей, являющихся натуральными числами. Пересчитаем то количество, что у нас получилось в предыдущей задаче, и убедимся в правильности решения. Если учесть и отрицательные делители, которых столько же, сколько и положительных, то получится, что у данного числа всего будет 72 делителя.
Условие: определите, сколько делителей имеет 84 .
Решение
Раскладываем число на множители.
84 42 21 7 1 2 2 3 7
Записываем каноническое разложение: 84 = 2 2 · 3 · 7 . Определяем, сколько у нас получится положительных делителей: ( 2 + 1 ) · ( 1 + 1 ) · ( 1 + 1 ) = 12 . Для учета отрицательных нужно умножить это число на 2 : 2 · 12 = 24 .
Ответ: всего у 84 будет 24 делителя – 12 положительных и 12 отрицательных.
Видео
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Примеры:
10 : 5 = 2
100 : 5 = 20
100 : 2 = 50
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Примеры:
355 : 5 = 71
200 : 5 = 40
475 : 5 = 95
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
27 : 3 = 9
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
18 : 9 = 2
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
Определение [ править
Функция «сумма положительных делителей »σx(n) для вещественного или комплексного числа x определяется как сумма x-х степеней положительных делителей числа n. Функцию можно выразить формулой
σ x ( n ) = ∑ d | n d x , <displaystyle sigma _(n)=sum _d^,!,>
где d | n <displaystyle > 
Аликвотная сумма s(n) для n — это сумма собственных делителей (то есть делители, за исключением самого n [5] , и равна σ1(n) − n. Аликвотная последовательность для n образуется последовательным вычислением аликвотной суммы, то есть каждое последующее значение в последовательности равно аликвотной сумме предыдущего значения.
Как найти число простых делителей числа
Если речь идет о целом малом числе, то решение такой задачи не представляет никакой сложности. Рассмотрим конкретный пример. Найдем простые делители числа 54.
Для этого:
- 54 делим на «два» и получаем 27;
- 27 нечетное, поэтому разделим его уже не на «два», а на следующее простое число, т. е. «три»;
- заметим, что 27=33;
- таким образом, разложение 54 имеет вид 54 = 21 * 33, т.е. простые делители числа 54 — это «два» и «три».
Однако это не все, что мы хотели знать. Теперь найдем число простых делителей числа 54. Оно равно произведению степеней простых множителей канонического разложения числа n = p1*d1 p2d2*⋅ …⋅*pmdm, увеличенных на 1. Иными словами, в общем случае K = (d1+1)*…* (dm+1).
Тогда для 54 имеем К = 2 * 4 = 8, т. е. общее число делителей равно восьми.
Обратите внимание, что все значительно упростилось, если бы речь шла о 23, 37, 103 и пр., так как каждый знает, сколько делителей у простого числа.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
5 : 1 = 5
5 : 5 = 1
Значит, число 5 является простым числом.
Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1
4 : 4 = 1
4 : 2 = 2
4 : 1 = 4
Значит, число 4 является составным числом.
Чем отличаются друг от друга, как найти
Делитель отличается от кратного тем, что:
- делитель — это число, НА которое делится заданное число;
- кратное — это число, которое само ДЕЛИТСЯ НА заданное число.
Чтобы найти делители числа, нужно данное число разложить на множители.
Разложить на множители — представить число в виде произведения целых чисел.
Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.
Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.
Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.
Тест Миллера Рабина
В криптографических целях часто используют именно этот вид определения простоты числа, который имеет несколько модификаций.
Тест Миллера—Рабина основан на проверке ряда условий, выполняемых для чисел, которые делятся только на 1 и на самих себя. Если хотя бы одно из требований нарушено, это «экзаменуемое» число признается составным.
Для данного m находятся целые нечетное число t и s, такие чтобы выполнялось условие m-1=2st.
Затем выбирается случайное число a, такое что 1<a<m. Если a не свидетельствует о простоте числа m, то программа должна выдать ответ «m составное» и завершить свою работу. В противном случае выбирается другое случайное число a и проверка повторяется снова. После того как будут установлены r свидетелей простоты, должен быть выдан ответ «m, вероятно, простое», и алгоритм завершит свою работу.
Следствием теоремы Рабина является тот факт, что если r чисел, которые выбраны случайно, признаны свидетелями для определения простоты числа m, то вероятность того, что оно составное, не может превосходить (4-r).
Теперь вы знаете, сколько делителей имеет простое число и как выяснить наиболее примитивный алгоритм вычисления НПД. Эти знания помогут вам в решении многих практических задач.
Теги
Собственный делитель
Предмет
Высшая математика
Разместил
🤓 tiovulrires1977660
👍 Проверено Автор24
делитель числа, отличный от самого этого числа; напр., собственными делителями числа 130 являю тся 1, 2, 5, 10, 13, 26 и 65
Научные статьи на тему «Собственный делитель»
Фондовая биржа как профессиональный участник фондового рынка. Биржевые индексы
Депозитарий представляет собой хранилище, где ведется учет прав собственности на ценные бумаги….
Например, индекс взвешенный по цене рассчитывается, как сумма всех активов, которая делится на делитель…
Размер делителя сохраняется при всех исчислениях для того, чтобы добавлять или исключать компании из…
Для этого суммируются капитализации всех участвующих в торгах компаний и делятся на общий делитель….
Делитель выбирается в зависимости от особенностей момента расчета.

Статья от экспертов
О вычислении псевдообратной матрицы. Общий случай
Предложен универсальный подход аналитического вычисления псевдообратной матрицы как для прямоугольной, так и для квадратной матриц. На основе этого подхода получена формула, связывающая операцию обращения невырожденной блочной матрицы, составленной из заданной матрицы и ее левого и правого делителей нуля максимального ранга, собственно с псевдообращением этой матрицы. Приведена теорема и ее доказательство. Исследованы основные свойства указанной формулы. Сформулированы следствия, имеющие практическое значение и упрощающие вычисление псевдообратной матрицы. Рассмотрены как полуортогональные матричные делители нуля, так и матрицы, не имеющие этого свойства. Приведены примеры иллюстративного характера, связанные с обращением символьной матрицы как квадратного, так и прямоугольного вида невысокого ранга
Высоковольтные выключатели
Собственное время отключения….
дугогасительная камера; 3 — шунтирующий резистор; 4 — главные контакты; 5 — отделитель; 6 — емкостный делитель…
зависимости от конструкции высоковольтные воздушные выключатели делятся на выключатели с газонаполненным делителем

Статья от экспертов
Универсальный критерий для расчета параметров нелинейного колебательного контура с периодически изменяющимся параметром
Показано, что выполнение условия равенства среднего за период значения собственной частоты параметрических колебаний позволяет получить соотношения между электромагнитными и конструктивными параметрами делителя частоты на границе возникновения колебаний половинной частоты и в стационарном режиме. Полученные соотношения позволяют произвести расчеты с достаточной точностью.I
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек