Алгоритм: Как найти следующую лексикографическую перестановку
Время на прочтение
3 мин
Количество просмотров 33K
Если кратко описать, что такое лексикографический порядок — это сортировка в алфавитном порядке. Т.е. последовательность символов — AAA → AAB → AAC → AAD → ……… → WWW — является отсортированной в алфавитном (или в нашем случае лексикографическом) порядке.
Представьте, что у Вас есть конечная последовательность символов, например 0, 1, 2, 5, 3, 3, 0 и Вам необходимо найти все возможные перестановки этих символов. Наиболее интуитивным, но и наибольшим по сложности, является рекурсивный алгоритм, когда мы выбираем первый символ из последовательности, далее рекурсивно выбираем второй, третий итд, до тех пор, пока все символы из последовательности не будет выбраны. Понятно, что сложность такого алгоритма — O(n!).
Но оказывается, что наиболее простой алгоритм генерации всех перестановок в лексикографическом порядке — это начать с наименьшей и многократно вычислять следующую перестановку на месте. Давайте посмотрим как это сделать.
Точно также, как при расчете следующего целочисленного значения, мы должны стараться увеличить правую часть последовательности и оставить левую часть неизменной.
В качестве примера возьмем вышеприведенную последовательность — (0, 1, 2, 5, 3, 3, 0). Чтобы получить последовательность выше оригинальной, достаточно переставить первый и второй элементе местами, но в этом нет необходимости, так как можно переставить второй и и третий и получив более близкую по возрастанию последовательность. что приведет нас к следующей более близкой перестановки итд.
Наиболее оптимальным алгоритмом в этом случае будет следующий:
- Прежде всего Вы должны найти наибольший не-увеличивающийся суффикс. В вышеприведенном примере это будет — (5, 3, 3, 0). Если Вы попробуете сделать любую перестановку в данной последовательности, то она не будет выше оригинальной.
Стоит сказать, что найти данную последовательность вы можете за O(n) времени, просматривая последовательность слева направо. - Следующий элемент от суффикса является точкой поворота. В нашем случае — это 2. Точка поворота будет всегда меньше первого элемента суффикса. Это значит, что в суффиксе обязательно будет элемент превышающий точку поворота и если мы поменяет точку поворота на наименьший элемента из суффикса, превышающий опорный элемент точки поворота — мы получим последовательность превышающую оригинальную — в нашем случает это будет — (0, 1, 3, 5, 3, 2, 0).
Т.е. результатом этой операции будет минимально возможный по возрастанию префикс. - И на последнем шаге мы должны отсортировать суффикс в порядке возрастания. Т.е. мы получим минимально возможный суффикс. В нашем примере это будет (0, 2, 3, 5) и вся последовательность будет выглядеть как (0, 1, 3, 0, 2, 3, 5).
Это значение и будет следующей лексикографической перестановкой.
Что касается практического применения алгоритма, то за все время моей работы он мне ни разу не понадобился, но на интервью в Uber посчитали иначе :))
Для простоты весь код будет написан на Go и думаю никому не составить труда перевести его на любой другой язык программирования.
Большое спасибо PYXRU и 646f67, что ткнули меня носом в возможную оптимизацию алгоритма — произвести расчет перестановки за линейную сложность просто сделав reverse суффикса.
func NextPermutationAlgorithm(w string) string {
l := len(w)
b := []byte(w)
r := "no answer"
for i:=l-1; i>0 ; i--{
if b[i-1] < b[i] {
pivot := i
for j := pivot; j < l; j++ {
if b[j] <= b[pivot] && b[i-1] < b[j] {
pivot = j
}
}
b[i-1], b[pivot] = b[pivot], b[i-1]
for j := l-1; i < j; i, j = i+1, j-1 {
b[i], b[j] = b[j], b[i]
}
r = string(b)
break
}
}
return r
}

Построение перестановки по таблице инверсий справа
налевоВход
N > 0 — количество элементов перестановки
b1, b2 …, bN – ТИ, 0 ≤ bj ≤ N − j
Алгоритм
П= пустая последовательность
цикл по j от N вниз до 1
вставить число j в П после bj элементов конец цикла
Выход
П− перестановка, соответствующая ТИ

Построение перестановки по таблице инверсий слева
направоСоздается заготовка пустой перестановки длины N
На каждом шаге для каждого элемента перестановки, начиная с 1, отсчитывается в ней столько пустых ячеек, какое число записано в соответствующей позиции в таблице инверсий
В следующее за ними пустое место вставляется этот элемент
|
Таблица инверсий |
3 6 4 0 2 2 1 |
|
0 |
|
5 |
9 |
1 |
8 |
2 |
6 |
4 |
7 |
3 |
|
Перестановка |

Построение перестановки по таблице инверсий слева
направоВход
N > 0 — количество элементов перестановки b1, b2 …, bN – ТИ, 0 ≤ bj ≤ N − j
Алгоритм
П= последовательность из N пустых элементов
цикл по i от 1 до N с шагом 1 выполнять пропустить bi пустых мест в P
поместить i на следующее пустое место конец цикла
Выход
П− перестановка, соответствующая ТИ

Инверсионный метод поиска всех перестановок
Таблицы инверсий взаимно однозначно соответствуют перестановкам
Почему?
Перебор ТИ сводится к перебору перестановок и наоборот

Инверсионный метод поиска всех перестановок
Рассмотрим таблицу инверсий как N-значное число в «системе счисления», где количество цифр, которое можно использовать в i-м разряде (с конца, начиная с 0) равно i
Возьмем «нулевую» таблицу и будем последовательно прибавлять к ней в нашей СС единицу, пользуясь алгоритмом сложения с переносом для многоразрядных чисел
Последовательно получим все ТИ и для каждой восстановим перестановку

Генерация таблиц инверсии
|
4 |
3 |
2 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
Шаг 0 |
|
0 |
0 |
0 |
1 |
0 |
Шаг 1 |
|
0 |
0 |
1 |
0 |
0 |
Шаг 2 |
|
0 |
0 |
1 |
1 |
0 |
Шаг 3 |
|
0 |
0 |
2 |
0 |
0 |
Шаг 4 |
|
0 |
0 |
2 |
1 |
0 |
Шаг 5 |
|
0 |
1 |
0 |
0 |
0 |
Шаг 6 |
|
0 |
1 |
0 |
1 |
0 |
Шаг 7 |
|
0 |
1 |
1 |
0 |
0 |
Шаг 8 |
|
0 |
1 |
1 |
1 |
0 |
Шаг 9 |
|
0 |
1 |
2 |
0 |
0 |
Шаг 10 |
|
… |
… |
… |
… |
… |
… |
|
4 |
3 |
2 |
1 |
0 |
Шаг 119 |

Нахождение следующей таблицы инверсий
B = b1, b2, …, bN – ТИ
i = N
не_всё = истина пока не_всё
x = bi + 1
если x > N – i то bi = 0
i = i – 1 иначе bi = x
не_всё = ложь всё
всёЧто же тут не так?

Поиск следующей по алфавиту перестановки
(алгП. b .=Дейкстры)b1, b2, …, bN предшествует п. c = c1, c2, …, cN в алфавитном (лексико
графическом) порядке, если b1=c1, b2=c2, …, b[k-1]=c[k-1] и bk < сk для некоторого k
Перестановка 1 2 3 4 5 предшествует перестановке 1 2 4 5 3 (k = 3)
Первой перестановкой в алфавитном порядке является перестановка 1,2,3, …, N, а последней — N, N-1, N-2, …, 1

Алгоритм Дейкстры
От заданной перестановки перейдем к следующей за ней в алфавитном порядке и т.д., пока не получим N, N-1, …, 1
Например, для перестановки
1 4 6 2 9 5 8 7 3 следующей по алфавиту является
|
перестановка |
1 4 6 2 9 7 3 5 8 |

Генерация следующей по алфавиту перестановки
Вход
П= a1, a2, …, a[N-1], aN – перестановка N > 0
элементов
Алгоритм Начиная с последнего элемента, найдем такой
номер i, что ai+1 > … > aN и ai < a[i+1]
Если такого i нет, то П – последняя в алф. порядке Обозначим aj наименьший элемент среди тех a[i+1], …, aN, которые строго больше ai Поменяем местами ai и aj
Упорядочим a[i+1], …, aN по возрастанию
Выход
Cледующая по алфавиту перестановка
Этот онлайн калькулятор иллюстрирует работу нерекурсивного алгоритма Нарайаны для генерации перестановок в лексикографическом порядке. Вы вводите элементы начальной перестановки, разделенные запятыми, и количество итераций алгоритма (перестановка, полученная на предыдущей итерации, является начальной перестановкой следующей итерации). Данные по умолчанию — перестановка 1,2,3 и количество итераций 6 генерируют все возможные перестановки из трех элементов (три факториал) и возвращают к начальной перестановке.
Это иллюстрирует тот факт, что если алгоритм Нарайаны применить в цикле к исходной последовательности из элементов
, упорядоченных так, что
, то он сгенерирует все перестановки элементов множества
в лексикографическом порядке1.
Описание алгоритма можно прочитать под калькулятором.
Алгоритм Нарайаны
Элементы перестановки, разделенные запятой
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Алгоритм Нарайаны
- Найти такой наибольший
, для которого
.
- Увеличить
. Для этого надо найти наибольшее
, для которого
. Затем поменять местами
и
.
- Записать последовательность
в обратном порядке.
Алгоритм придуман индийским математиком Пандитом Нарайаной в XIV веке.
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Лекция 6
Перестановки
Слайд 2
Описание слайда:
Перестановки
Перестановкой порядка N называется расположение N различных объектов в ряд в некотором порядке.
Например, для трех объектов — а, b и с — существует шесть
перестановок:
аbс, acb, bac, bса. cab, cba.
Для множества из N элементов можно построить N! различных перестановок: первую позицию можно занять N способами, вторую — (N – 1) способом, так как один элемент уже занят, и т. д. На последнее место можно поставить только один оставшийся элемент.
Следовательно, общее количество вариантов расстановки равно
N (N −1) (N − 2) … 1 = N!
Далее будем рассматривать перестановки элементов множества
{1, 2, 3, … , N}
Слайд 3
Описание слайда:
Инверсии
Пусть даны базовое множество из N элементов 1,2, 3,…, N и его перестановка
Пара называется инверсией (инверсионной парой) перестановки ,
если при i < j.
Например, перестановка 4, 1, 3, 2 имеет четыре инверсии:
(4,1), (3,2), (4,3) и (4,2).
Единственной перестановкой, не содержащей инверсий, является упорядоченная перестановка 1, 2, 3, … , N.
Таким образом, каждая инверсия — это пара элементов
перестановки, нарушающих ее упорядоченность.
Слайд 4
Описание слайда:
Таблицей инверсий перестановки a1,a2, …,aN называется последовательность чисел b1, b2 …, bN , где bj есть число элементов перестановки, больших j и расположенных левее j
Таблицей инверсий перестановки a1,a2, …,aN называется последовательность чисел b1, b2 …, bN , где bj есть число элементов перестановки, больших j и расположенных левее j
(т. е. количество инверсий вида (x, j), при x > j).
Например,
для перестановки 5 9 1 8 2 6 4 7 3
таблица инверсий: 2 3 6 4 0 2 2 1 0.
Свойство элементов таблицы инверсий:
bN = 0,
…
0 ≤ bi ≤ N – i ,
…
0 ≤ b1 ≤ N – 1.
Утверждение
Таблица инверсий единственным образом определяет соответствующую ей перестановку.
Слайд 5
Описание слайда:
Построение перестановки по таблице инверсий
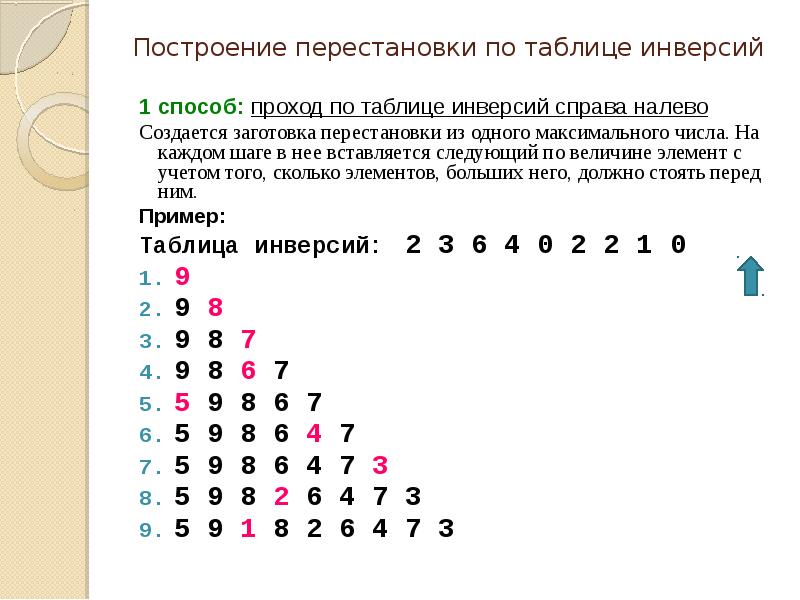
1 способ: проход по таблице инверсий справа налево
Создается заготовка перестановки из одного максимального числа. На каждом шаге в нее вставляется следующий по величине элемент с учетом того, сколько элементов, больших него, должно стоять перед ним.
Пример:
Таблица инверсий: 2 3 6 4 0 2 2 1 0
9
9 8
9 8 7
9 8 6 7
5 9 8 6 7
5 9 8 6 4 7
5 9 8 6 4 7 3
5 9 8 2 6 4 7 3
5 9 1 8 2 6 4 7 3
Слайд 6
Описание слайда:
Алгоритм П1:
построение перестановки по таблице инверсий справа налево
Вход:
N > 0 — количество элементов перестановки,
b1, b2 …, bN – таблица инверсий,
0 ≤ bj ≤ N − j.
Р := пустая последовательность;
цикл по j от N вниз до 1
вставить число j в Р после bj элементов;
конец цикла;
Выход:
Р − перестановка, соответствующая данной таблице инверсий
Слайд 7
Описание слайда:
Построение перестановки по таблице инверсий
2 способ: проход по таблице инверсий слева направо
Создается заготовка пустой перестановки длины N.
На каждом шаге для каждого элемента перестановки, начиная с 1, отсчитывается в ней столько пустых ячеек, какое число записано в соответствующей позиции в таблице инверсий. В следующее за ними пустое место вставляется этот элемент.
Пример:
Таблица инверсий: 2 3 6 4 0 2 2 1 0
Перестановка:
Слайд 8
Описание слайда:
Алгоритм П2:
построение перестановки по таблице инверсий слева направо
Вход:
N > 0 — количество элементов перестановки,
b1, b2 …, bN – таблица инверсий,
0 ≤ bj ≤ N − j.
Р := последовательность из N пустых элементов;
цикл по i от 1 до N с шагом 1 выполнять
пропустить bi пустых мест в P;
поместить i на следующее пустое место;
конец цикла
Выход:
Р − перестановка, соответствующая данной таблице инверсий
Слайд 9
Описание слайда:
Инверсионный метод поиска всех перестановок
Таблица инверсий однозначно определяет перестановку и каждая перестановка имеет только одну таблицу инверсий.
Следовательно, если мы сумеем перебрать все таблицы инверсий, то с помощью алгоритмов П1 или П2 сможем по ним восстановить все перестановки.
Рассмотрим таблицу инверсий как N-значное число в такой необычной «системе счисления»: количество цифр, которое можно использовать в i-м разряде (с конца, начиная с 0) равно i.
Возьмем «минимальную» таблицу и будем последовательно прибавлять к ней, как к числу, единицу, пользуясь, например, алгоритмом сложения с переносом для многоразрядных чисел, модифицированным для нашей «системы счисления».
Слайд 10
Описание слайда:
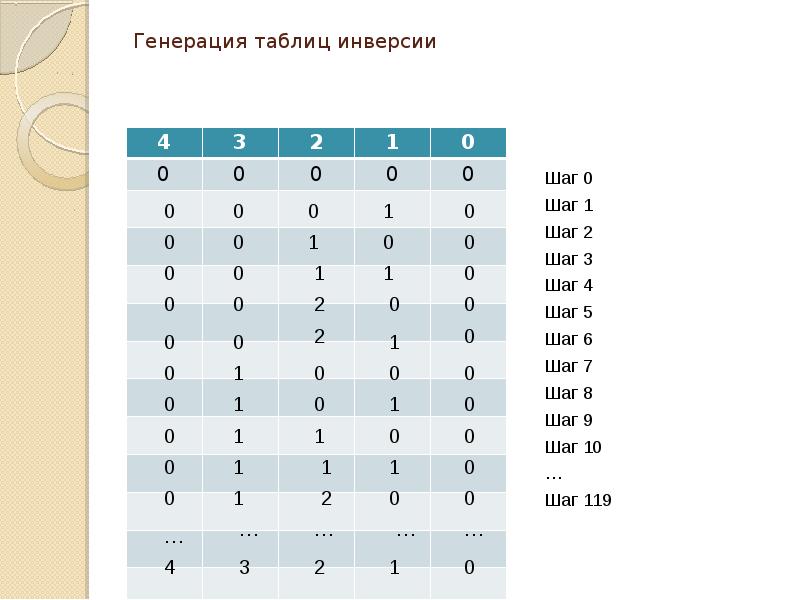
Генерация таблиц инверсии
Слайд 11
Описание слайда:
Алгоритм И1:
нахождение следующей таблицы инверсий
Пусть B = b1, b2, …, bN – таблица инверсий, построенная на предыдущем шаге.
Тогда следующая таблица инверсий получается из нее прибавлением к ней единицы:
i := N;
flag := истина;
пока flag выполнять
x := bi + 1;
если x > N – i
то
начало
bi := 0;
i := i –1;
конец
иначе
начало
bi := x;
flag := ложь;
конец
конец пока
Слайд 12
Описание слайда:
Алгоритм Дейкстры:
поиск следующей по алфавиту перестановки
Пусть даны две перестановки
b = b1, b2 …, bN и
c = c1, c2 …, cN
набора 1, 2, …, N.
Говорят, что перестановка b предшествует перестановке с в алфавитном (лексикографическом) порядке, если для минимального значения k, такого что bk ≠ ck, справедливо bk < сk.
Например, перестановка 1 2 3 4 5 предшествует перестановке 1 2 4 5 3 (здесь k = 3).
Первой перестановкой в алфавитном порядке является
перестановка 1,2,3, …, N,
а последней — N,N-1,N-2,…,1
Слайд 13
Описание слайда:
Идея алгоритма Дейкстры:
определить каким-либо образом функцию, которая по заданной перестановке выдает непосредственно следующую за ней в алфавитном порядке, и применять ее последовательно к собственным результатам начиная с самой первой перестановки, пока не будет получена последняя.
Например, для перестановки
1 4 6 2 9 5 8 7 3
следующей по алфавиту является перестановка
1 4 6 2 9 7 3 5 8.
Слайд 14
Описание слайда:
Алгоритм Дейкстры:
генерация следующей по алфавиту перестановки
Вход: N > 0 — количество элементов;
a1, a2, …, aN-1, aN – предыдущая перестановка.
Шаг 1. Просматривая перестановку, начиная с последнего элемента, найдем такой номер i, что ai+1 > … > aN и ai < ai+1.
Если такого i нет, то последовательность упорядочена по убыванию и следующей перестановки нет: конец алгоритма.
Шаг 2. Найти в «хвосте» ai+1, …, aN элемент aj,, такой что i+1 j N, aj есть наименьшее значение, удовлетворяющее условию aj > ai. После этого поменять местами ai и aj .
Шаг 3. Упорядочить «хвост» ai+1, …, aN по возрастанию. Для этого достаточно его инвертировать (обернуть в обратном порядке).
Выход: следующая по алфавиту перестановка за данной.
Слайд 15
Описание слайда:
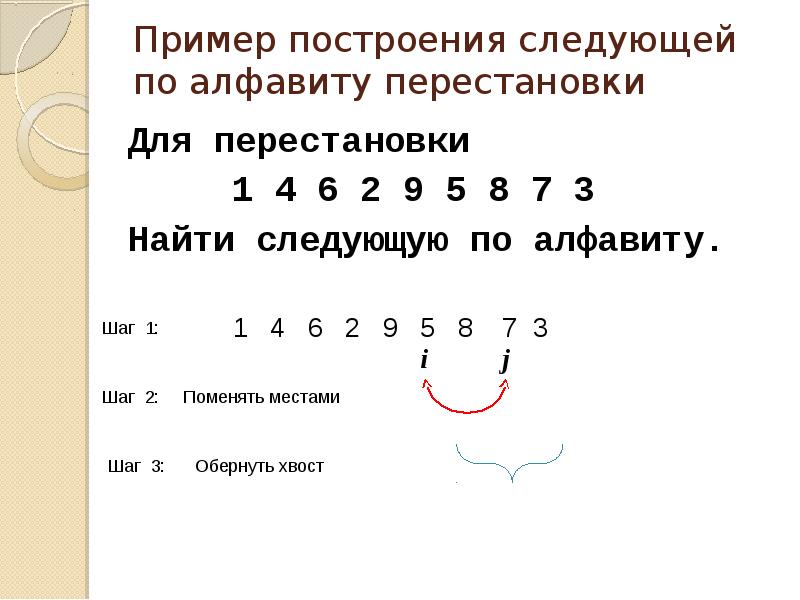
Пример построения следующей по алфавиту перестановки
Для перестановки
1 4 6 2 9 5 8 7 3
Найти следующую по алфавиту.
Слайд 16
Описание слайда:
Рекурсивный метод поиска всех перестановок
Метод рекурсивного перебора перестановок основан на идее сведения исходной задачи к аналогичной задаче на меньшем наборе входных данных.
Система рекуррентных соотношений, определяющих множество Реr(М) всех перестановок базового множества М произвольной природы:
Реr(0) = {«»},
Реr(М) = Permut(i, M{i}),
Permut(i, S) = {«i» + s s Per(S) }.
Первое равенство задает условие обрыва рекурсивного спуска: пустое множество элементов порождает пустую перестановку.
Два последних равенства определяют правила рекурсивного перехода.
Слайд 17
Описание слайда:
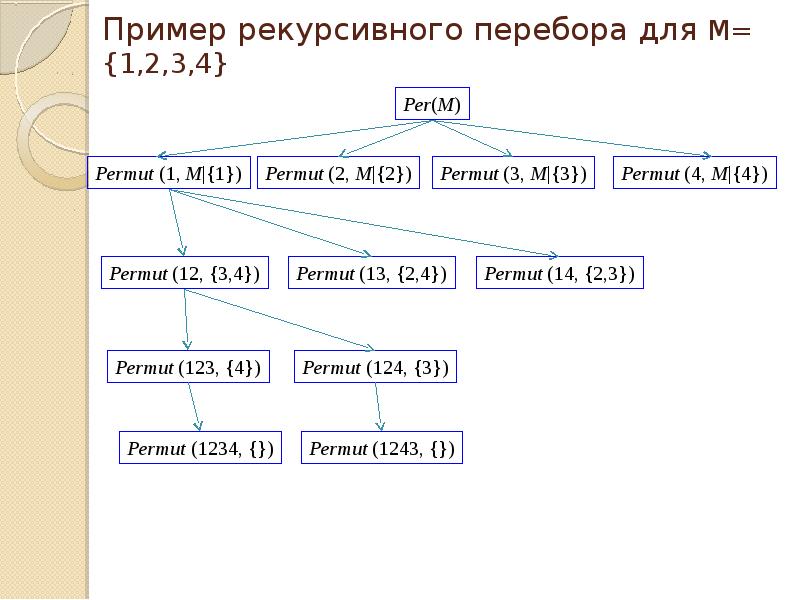
Пример рекурсивного перебора для M= {1,2,3,4}
Слайд 18
Описание слайда:
На языке Си этот процесс можно описать следующим образом:
typedef char string[256];
void permut(string start, string rest)
{
int lenr = strlen(rest);
int lens = strlen(start);
int i=0; string sl=“»; string s2=“»;
if (lenr == 0) Printf(“%sn”, start);
else
{
for (i = 0; i < lenr; i++)
{
/* Добавляем i-ый символ к строке start */
strcpy(sl,start);
strncpy(sl+lens,rest+i,1);
strncpy(sl+lens+1,»»,1);
/* Удаляем i-ый символ из строки rest */
strncpy(s2,rest,i);
strncpy(s2+i,rest+i+l,lenr-i-1);
strncpy(s2+lenr-l,»», 1);
/* Рекурсивный переход */
permut( s1, s2 );
}
}
}
Слайд 19
Описание слайда:
Генерация всех перестановок методом Кнута
Идея:
если построены все перестановки длины N, то для каждой такой перестановки можно построить N+1 перестановку длины N+1.
Пример:
Для перестановки 3241 можно построить 5 различных перестановок длины 5:
53241
35241
32541
32451
32415
Слайд 20
Описание слайда:
Генерация перестановок методом Кнута –
1 способ
Пусть дана перестановка длины N.
Дописать в конец перестановки числа (2i+1)/2 (0 i N).
Перенумеровать элементы полученных перестановок в порядке их возрастания.
Пример: дана перестановка 3241.
3 2 4 1 0.5 4 3 5 2 1
3 2 4 1 1.5 4 3 5 1 2
3 2 4 1 2.5 4 2 5 1 3
3 2 4 1 3.5 3 2 5 1 4
3 2 4 1 4.5 3 2 4 1 5
Слайд 21
Описание слайда:
Генерация перестановок методом Кнута –
2 способ
Пусть дана перестановка длины N: a1 a2 … aN .
Дописать в конец перестановки числа k
(1 k N +1).
Для всех ai k заменить их на ai + 1.
Пример: дана перестановка 3241.
3 2 4 1 1 4 3 5 2 1
3 2 4 1 2 4 3 5 1 2
3 2 4 1 3 4 2 5 1 3
3 2 4 1 4 3 2 5 1 4
3 2 4 1 5 3 2 4 1 5
Слайд 22
Описание слайда:
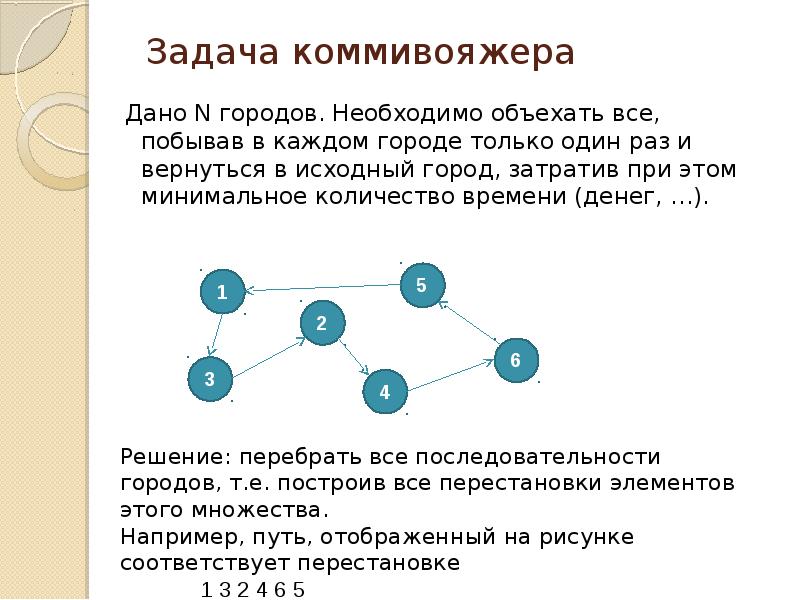
Задача коммивояжера
Дано N городов. Необходимо объехать все, побывав в каждом городе только один раз и вернуться в исходный город, затратив при этом минимальное количество времени (денег, …).
1
Лекция 4 Перестановки
2
Перестановки Перестановкой порядка N называется расположение N различных объектов в ряд в некотором порядке. Например, для трех объектов а, b и с существует шесть перестановок: аbс, acb, bac, оса. cab, cba. Для множества из N элементов можно построить N! различных перестановок: первую позицию можно занять N способами, вторую (N – 1) способом, так как один элемент уже занят, и т. д. На последнее место можно поставить только один оставшийся элемент. Следовательно, общее количество вариантов расстановки равно N (N 1) (N 2)… 1 = N! Далее будем рассматривать перестановки элементов множества {1, 2, 3, …, N}
3
Инверсии Пусть даны базовое множество из N элементов 1,2, 3,…, N и его перестановка Пара называется инверсией (инверсионной парой) перестановки, если при i < j. Например, перестановка 4, 1, 3, 2 имеет четыре инверсии: (4,1), (3,2), (4,3) и (4,2). Единственной перестановкой, не содержащей инверсий, является упорядоченная перестановка 1, 2, 3,…, N. Таким образом, каждая инверсия это пара элементов перестановки, нарушающих ее упорядоченность.
4
Таблицей инверсий перестановки a 1,a 2,…,a N называется последовательность чисел b 1, b 2 …, b N, где b j есть число элементов перестановки, больших j и расположенных левее j (т. е. количество инверсий вида (x, j), при x > j). Например, для перестановки таблица инверсий: Свойство элементов таблицы инверсий: b N = 0, … 0 b i N – i, … 0 b 1 N – 1. Утверждение Таблица инверсий единственным образом определяет соответствующую ей перестановку.
5
Построение перестановки по таблице инверсий 1 способ: проход по таблице инверсий справа налево Создается заготовка перестановки из одного максимального числа. На каждом шаге в нее вставляется следующий по величине элемент с учетом того, сколько элементов, больших него, должно стоять перед ним. Пример: Таблица инверсий:
6
Алгоритм A1: построение перестановки по таблице инверсий справа налево Вход: N > 0 — количество элементов перестановки, b 1, b 2 …, b N – таблица инверсий, 0 b j N j. Р := пустая последовательность; цикл по j от N вниз до 1 вставить число j в Р после b j элементов; конец цикла; Выход: Р перестановка, соответствующая данной таблице инверсий
7
Построение перестановки по таблице инверсий 2 способ: проход по таблице инверсий слева направо Создается заготовка пустой перестановки длины N. На каждом шаге для каждого элемента перестановки, начиная с 1, отсчитывается в ней столько пустых ячеек, какое число записано в соответствующей позиции в таблице инверсий. В следующее за ними пустое место вставляется этот элемент. Пример: Таблица инверсий: Перестановка:
8
Алгоритм A2: построение перестановки по таблице инверсий слева направо Вход: N > 0 — количество элементов перестановки, b 1, b 2 …, b N – таблица инверсий, 0 b j N j. Р := последовательность из N пустых элементов ; цикл по i от 1 до N с шагом 1 выполнять пропустить b i пустых мест в P; поместить i на следующее пустое место; конец цикла Выход: Р перестановка, соответствующая данной таблице инверсий
9
Инверсионный метод поиска всех перестановок Таблица инверсий однозначно определяет перестановку и каждая перестановка имеет только одну таблицу инверсий. Следовательно, если мы сумеем перебрать все таблицы инверсий, то с помощью алгоритмов П1 или П2 сможем по ним восстановить все перестановки. Рассмотрим таблицу инверсий как N-значное число в такой необычной «системе счисления»: количество цифр, которое можно использовать в i-м разряде (с конца, начиная с 0) равно i. Возьмем «минимальную» таблицу и будем последовательно прибавлять к ней, как к числу, единицу, пользуясь, например, алгоритмом сложения с переносом для многоразрядных чисел, модифицированным для нашей «системы счисления».
10
Генерация таблиц инверсии … 1 11 … … … … 43 2 Шаг 0 Шаг 1 Шаг 2 Шаг 3 Шаг 4 Шаг 5 Шаг 6 Шаг 7 Шаг 8 Шаг 9 Шаг 10 … Шаг 119
11
Алгоритм A 3 нахождение следующей таблицы инверсий Пусть B = b 1, b 2,…, b N – таблица инверсий, построенная на предыдущем шаге. Тогда следующая таблица инверсий получается из нее прибавлением к ней единицы: i := N; flag := истина; пока flag выполнять x := b i + 1; если x > N – i то начало b i := 0; i := i –1; конец иначе начало b i := x; flag := ложь; конец конец пока
12
Алгоритм Дейкстры : поиск следующей по алфавиту перестановки Пусть даны две перестановки b = b 1, b 2 …, b N и c = c 1, c 2 …, c N набора 1, 2,…, N. Говорят, что перестановка b предшествует перестановке с в алфавитном (лексикографическом) порядке, если для минимального значения k, такого что b k c k, справедливо b k < с k. Например, перестановка предшествует перестановке (здесь k = 3). Первой перестановкой в алфавитном порядке является перестановка 1,2,3,…, N, а последней N,N-1,N-2,…,1
13
Идея алгоритма Дейкстры : определить каким-либо образом функцию, которая по заданной перестановке выдает непосредственно следующую за ней в алфавитном порядке, и применять ее последовательно к собственным результатам начиная с самой первой перестановки, пока не будет получена последняя. Например, для перестановки следующей по алфавиту является перестановка
14
Алгоритм Дейкстры : генерация следующей по алфавиту перестановки Вход: N > 0 количество элементов; a 1, a 2, …, a N-1, a N – предыдущая перестановка. Шаг 1. Просматривая перестановку, начиная с последнего элемента, найдем такой номер i, что a i+1 >… > a N и a i < a i+1. Если такого i нет, то последовательность упорядочена по убыванию и следующей перестановки нет: конец алгоритма. Шаг 2. Найти в «хвосте» a i+1, …, a N элемент a j,, такой что i+1 j N, a j есть наименьшее значение, удовлетворяющее условию a j > a i. После этого поменять местами a i и a j. Шаг 3. Упорядочить «хвост» a i+1, …, a N по возрастанию. Для этого достаточно его инвертировать (обернуть в обратном порядке). Выход: следующая по алфавиту перестановка за данной.
15
Пример построения следующей по алфавиту перестановки Для перестановки Найти следующую по алфавиту ij Шаг 1: Шаг 2: Шаг 3: Поменять местами Обернуть хвост
16
Рекурсивный метод поиска всех перестановок Метод рекурсивного перебора перестановок основан на идее сведения исходной задачи к аналогичной задаче на меньшем наборе входных данных. Система рекуррентных соотношений, определяющих множество Реr(М) всех перестановок базового множества М произвольной природы: Реr(0) = {«»}, Реr(М) = Permut(i, M{i}), Permut(i, S) = {«i» + s s Per(S) }. Первое равенство задает условие обрыва рекурсивного спуска: пустое множество элементов порождает пустую перестановку. Два последних равенства определяют правила рекурсивного перехода.
17
Пример рекурсивного перебора для M= {1,2,3,4} Реr(M) Реrmut (1, M|{1})Реrmut (2, M|{2})Реrmut (3, M|{3})Реrmut (4, M|{4}) Реrmut (12, {3,4})Реrmut (13, {2,4})Реrmut (14, {2,3}) Реrmut (123, {4})Реrmut (124, {3}) Реrmut (1234, {})Реrmut (1243, {})
18
На языке Си этот процесс можно описать следующим образом: typedef char string[256]; void permut(string start, string rest) { int lenr = strlen(rest); int lens = strlen(start); int i=0; string sl=»; string s2=»; if (lenr == 0) Printf(%sn, start); else { for (i = 0; i < lenr; i++) { /* Добавляем i-ый символ к строке start */ strcpy(sl,start); strncpy(sl+lens,rest+i,1); strncpy(sl+lens+1,»»,1); /* Удаляем i-ый символ из строки rest */ strncpy(s2,rest,i); strncpy(s2+i,rest+i+l,lenr-i-1); strncpy(s2+lenr-l,»», 1); /* Рекурсивный переход */ permut( s1, s2 ); } } }
19
Генерация всех перестановок методом Кнута Идея : если построены все перестановки длины N, то для каждой такой перестановки можно построить N+1 перестановку длины N+1. Пример: Для перестановки 3241 можно построить 5 различных перестановок длины 5:
20
Генерация перестановок методом Кнута – 1 способ Пусть дана перестановка длины N. Дописать в конец перестановки числа (2i+1)/2 (0 i N). Перенумеровать элементы полученных перестановок в порядке их возрастания. Пример: дана перестановка
21
Генерация перестановок методом Кнута – 2 способ Пусть дана перестановка длины N: a 1 a 2 … a N. Дописать в конец перестановки числа k (1 k N +1). Для всех a i k заменить их на a i + 1. Пример: дана перестановка
















![На языке Си этот процесс можно описать следующим образом:
typedef char string[256];
void permut(string start, string rest)
{
int lenr = strlen(rest);
int lens = strlen(start);
int i=0; string sl=“"; string s2=“";
if (lenr == 0) Printf(“%sn”, start);
else
{
for (i = 0; i < lenr; i++)
{
/* Добавляем i-ый символ к строке start */
strcpy(sl,start);
strncpy(sl+lens,rest+i,1);
strncpy(sl+lens+1,"",1);
/* Удаляем i-ый символ из строки rest */
strncpy(s2,rest,i);
strncpy(s2+i,rest+i+l,lenr-i-1);
strncpy(s2+lenr-l,"", 1);
/* Рекурсивный переход */
permut( s1, s2 );
}
}
}](https://myslide.ru/documents_3/70f74e7a8539d2d401db91efd0bc1c57/img17.jpg)