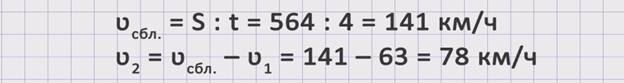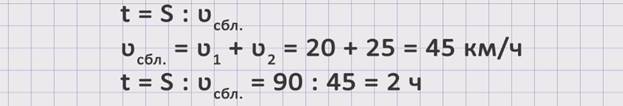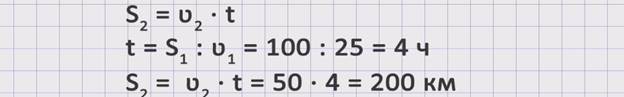Как найти скорость время расстояние видео

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

v=S/t, где

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

N=F*v*cos α , где N — механическая мощность,

F — сила,

v — скорость,

cos α — косинус угла между векторами силы и скорости.

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

S=v*t, где v — понятно что такое,

S — расстояние, которое требуется найти,

t — время, за которое объект прошел это расстояние.

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

t=S/v, где v — все та же скорость,

S — расстояние, пройденный путь,

t — время, значение которого в данном случае нужно найти.

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

§ 1  Встречное движение

В этом уроке мы познакомимся с задачами на встречное движение.

При решении любой задачи на движение мы сталкиваемся с такими понятиями, как «скорость», «время» и «расстояние».

Скорость – это расстояние, которое преодолевает объект за единицу времени. Измеряется скорость в км/ч, м/сек и т.д. Обозначается латинской буквой ʋ.

Время – это время, за которое объект преодолевает определенное расстояние. Измеряется время в секундах, минутах, часах и т.д. Обозначается латинской буквой t.

Расстояние – это путь, который преодолевает объект за определенное время. Измеряется расстояние в километрах, метрах, дециметрах и т.д. Обозначается латинской буквой S.

В задачах на движение эти понятия взаимосвязаны. Так, чтобы найти скорость, необходимо расстояние разделить на время: ʋ = S : t. Чтобы найти время, надо расстояние разделить на скорость: t = S : ʋ. А чтобы найти расстояние, скорость умножают на время: S = ʋ · t.

Говоря о задачах на встречное движение, используют понятие «скорость сближения». Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени. Обозначается ʋсбл..

Чтобы найти скорость сближения при встречном движении, зная скорости объектов, надо найти сумму этих скоростей: ʋсбл. = ʋ1 + ʋ2. Чтобы найти скорость сближения, зная время и расстояние, необходимо расстояние разделить на время: ʋсбл. = S : t.

§ 2  Решение задач

Рассмотрим взаимосвязь понятий «скорость», «время» и «расстояние» при решении задач на встречное движение.

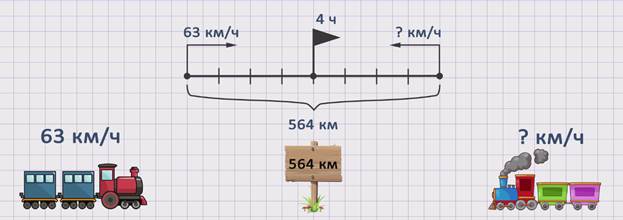
ЗАДАЧА 1. От двух станций, расстояние между которыми 564 км, одновременно навстречу друг другу вышли два поезда. Скорость одного из них — 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?

Изобразим движение поездов на схеме:

скорость первого поезда обозначим буквой ʋ1 = 63 км/ч. Скорость второго поезда обозначим буквой ʋ2 = ? км/ч. Время в пути обозначим буквой t = 4 ч. Расстояние, которое прошли оба поезда, — буквой S = 564 км.

Поскольку, чтобы найти неизвестную скорость, необходимо знать время, а оно известно и равно 4 часам, и расстояние, прошедшее вторым поездом до встречи, которое не указано в условиях задачи, то необходимо найти это расстояние.. Из условия задачи нам известно все расстояние S = 564 км, скорость первого поезда ʋ1 = 63 км/ч и время t = 4 ч. Зная расстояние, которое прошел до встречи первый поезд, мы сможем узнать и расстояние, которое прошел второй поезд. S1 = ʋ1 · t = 63 · 4 = 252 км. Значит, S2 = S – S1 = 564 – 252 = 312 км. Найдя расстояние, которое прошел до встречи второй поезд, можем найти и скорость второго поезда. ʋ2 = S2 : t = 312 : 4 = 78 км/ч. Получили, что скорость второго поезда равна 78 км/ч.

Рассмотрим второй вариант.

Поскольку, чтобы найти неизвестную скорость, необходимо знать скорость первого поезда, из условий задачи она известна ʋ1 = 63 км/ч, и скорость сближения, которая не оговаривается условиями задачи, то надо найти скорость сближения, используя данные задачи, а именно расстояние S = 564 км и время встречи t = 4 часа. Чтобы найти скорость сближения поездов, можно расстояние разделить на время. ʋсбл. = S : t = 564 : 4 = 141 км/ч. Теперь, зная скорость сближения, можем найти скорость второго поезда. ʋ2 = ʋсбл. — ʋ1 = 141 – 63 = 78 км/ч. Получили, что скорость второго поезда равна 78 км/ч.

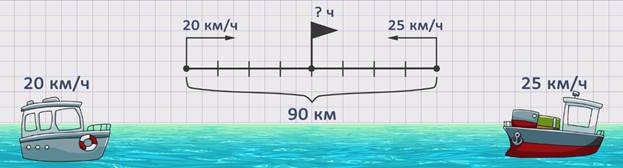
ЗАДАЧА 2. Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится, чтобы встретиться, если скорость первого составляет 20 км/час, а второго – 25 км/час?

Изобразим движение теплоходов на схеме.

Скорость первого теплохода обозначим буквой ʋ1 = 20 км/ч. Скорость второго теплохода обозначим буквой ʋ2 = 25 км/ч. Расстояние между пристанями обозначим буквой S = 90 км. Время – буквой t = ? часов.

Чтобы ответить на поставленный вопрос задачи, необходимо знать расстояние и скорость сближения, так как t = S : ʋсбл.. Поскольку расстояние нам известно из условия задачи, надо найти скорость сближения. ʋсбл. = ʋ1 + ʋ2 = 20 + 25 = 45 км/ч. Теперь, зная скорость сближения, можем найти неизвестное время. t = S : ʋсбл = 90 : 45 = 2 ч. Получаем, что теплоходам понадобится 2 часа, чтобы встретиться.

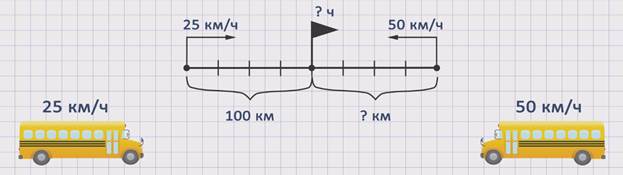
ЗАДАЧА 3. Из поселка и города навстречу друг другу одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость — 50 км/час?

Покажем движение автобусов на схеме.

Скорость первого автобуса обозначим буквой ʋ1 = 25 км /ч. Скорость второго автобуса обозначим буквой ʋ2 = 50 км/ч. Расстояние, которое до места встречи проехал первый автобус, обозначим буквой S1 = 100 км. Расстояние, которое проехал до встречи второй автобус – буквой S2 = ? км, а время – буквой t.

Чтобы ответить на вопрос задачи, необходимо знать скорость второго автобуса и время, которое он был в пути до встречи, так как S2 = ʋ2 · t. Поскольку скорость второго автобуса известна из условия задачи, надо найти время. Если мы найдем время, которое был в пути первый автобус, то мы найдем и время, которое был в пути второй автобус, так как они выехали одновременно, а это значит, что до момента встречи автобусы были в пути одинаковое количество времени. Чтобы найти время, можно расстояние, которое проехал первый автобус, разделить на его скорость. t = S1 : ʋ1 = 100 : 25 = 4 часа. Теперь, зная время, можем найти расстояние, которое второй автобус проехал до момента встречи. S2 = ʋ2 · t = 50 · 4 = 200 км. Получили, что второй автобус проехал до встречи 200 км.

§ 3  Краткие итоги по теме урока

При решение задач на встречное движение следует помнить, что в задачах такого типа выполняются следующие условия:

1.Объекты начинают свое движение одновременно навстречу друг другу, т.е. находятся в пути до встречи одинаковое количество времени; время обозначается латинской буквой t = S : ʋсбл;

2.Расстояние S – это сумма расстояний двух объектов до встречи; S = S1 + S2 или S = ʋсбл· t;

3.Объекты сближаются с определенной скоростью – скоростью сближения, обозначающейся латинской буквой ʋсбл. = S : t или ʋсбл = ʋ1 + ʋ2, соответственно ʋ1 = S1 : t и ʋ2 = S2 : t.