Download Article
Download Article
Velocity is defined as the speed of an object in a given direction.[1]
In many common situations, to find velocity, we use the equation v = s/t, where v equals velocity, s equals the total displacement from the object’s starting position, and t equals the time elapsed. However, this technically only gives the object’s average velocity over its path. Using calculus, it’s possible to calculate an object’s velocity at any moment along its path. This is called instantaneous velocity and it is defined by the equation v = (ds)/(dt), or, in other words, the derivative of the object’s average velocity equation.[2]
-
1
Start with an equation for velocity in terms of displacement. To get an object’s instantaneous velocity, first we have to have an equation that tells us its position (in terms of displacement) at a certain point in time. This means the equation must have the variable s on one side by itself and t on the other (but not necessarily by itself), like this:
s = -1.5t2 + 10t + 4
- In this equation, the variables are:
-
-
Displacement = s . The distance the object has traveled from its starting position.[3]
For example, if an object goes 10 meters forward and 7 meters backward, its total displacement is 10 — 7 = 3 meters (not 10 + 7 = 17 meters). - Time = t . Self explanatory. Typically measured in seconds.
-
Displacement = s . The distance the object has traveled from its starting position.[3]
-
- In this equation, the variables are:
-
2
Take the equation’s derivative. The derivative of an equation is just a different equation that tells you its slope at any given point in time. To find the derivative of your displacement formula, differentiate the function with this general rule for finding derivatives: If y = a*xn, Derivative = a*n*xn-1.This rule is applied to every term on the «t» side of the equation.[4]
- In other words, start by going through the «t» side of your equation from left to right. Every time you reach a «t», subtract 1 from the exponent and multiply the entire term by the original exponent. Any constant terms (terms which don’t contain «t») will disappear because they be multiplied by 0. This process isn’t actually as hard as it sounds — let’s derive the equation in the step above as an example:
s = -1.5t2 + 10t + 4
(2)-1.5t(2-1) + (1)10t1 — 1 + (0)4t0
-3t1 + 10t0
-3t + 10
Advertisement
- In other words, start by going through the «t» side of your equation from left to right. Every time you reach a «t», subtract 1 from the exponent and multiply the entire term by the original exponent. Any constant terms (terms which don’t contain «t») will disappear because they be multiplied by 0. This process isn’t actually as hard as it sounds — let’s derive the equation in the step above as an example:
-
3
Replace «s» with «ds/dt.» To show that our new equation is a derivative of the first one, we replace «s» with the notation «ds/dt». Technically, this notation means «the derivative of s with respect to t.» A simpler way to think of this is just that ds/dt is just the slope of any given point in the first equation. For example, to find the slope of the line made by s = -1.5t2 + 10t + 4 at t = 5, we would just plug «5» into t in its derivative.
- In our running example, our finished equation should now look like this:
ds/dt = -3t + 10
- In our running example, our finished equation should now look like this:
-
4
Plug in a t value for your new equation to find instantaneous velocity.[5]
Now that you have your derivative equation, finding the instantaneous velocity at any point in time is easy. All you need to do is pick a value for t and plug it into your derivative equation. For example, if we want to find the instantaneous velocity at t = 5, we would just substitute «5» for t in the derivative ds/dt = -3 + 10. Then, we’d just solve the equation like this:ds/dt = -3t + 10
ds/dt = -3(5) + 10
ds/dt = -15 + 10 = -5 meters/second- Note that we use the label «meters/second» above. Since we’re dealing with displacement in terms of meters and time in terms of seconds and velocity in general is just displacement over time, this label is appropriate.
Advertisement
-
1
Graph your object’s displacement over time. In the section above, we mentioned that derivatives are just formulas that let us find the slope at any point for the equation you take the derivative for.[6]
In fact, if you represent an object’s displacement with a line on a graph, the slope of the line at any given point is equal to the object’s instantaneous velocity at that point.[7]
- To graph an object’s displacement, use the x axis to represent time and the y axis to represent displacement. Then, just plot points by plugging values for t into your displacement equation, getting s values for your answers, and marking the t,s (x,y) points on the graph.
- Note that the graph can extend below the x axis. If the line representing your object’s motion drops below the x axis, this represents your object moving behind where it started. Generally, your graph won’t extend behind the y axis — we don’t often measure velocity for objects moving backward in time!
-
2
Choose one point P and a point Q that is near it on the line. To find a line’s slope at a single point P, we use a trick called «taking a limit.» Taking a limit involves taking two points (P, plus Q, a point near it) on the curved line and finding the slope of the line linking them over and over again as the distance between P and Q gets smaller.
- Let’s say that our displacement line contains the points (1,3) and (4,7). In this case, if we want to find the slope at (1,3), we can set (1,3) = P and (4,7) = Q.
-
3
Find the slope between P and Q. The slope between P and Q is the difference in y-values for P and Q over the difference in x-values for P and Q. In other words, H = (yQ — yP)/(xQ — xP), where H is the slope between the two points. In our example, the slope between P and Q is:
H = (yQ — yP)/(xQ — xP)
H = (7 — 3)/(4 — 1)
H = (4)/(3) = 1.33 -
4
Repeat several times, moving Q nearer to P. Your goal here is to make the distance between P and Q smaller and smaller until it gets close to a single point. The smaller the distance between P and Q gets, the closer the slope of your tiny line segments will be to the slope at point P. Let’s do this a few times for our example equation, using the points (2,4.8), (1.5,3.95), and (1.25,3.49) for Q and our original point of (1,3) for P:
Q = (2,4.8): H = (4.8 — 3)/(2 — 1)
H = (1.8)/(1) = 1.8Q = (1.5,3.95): H = (3.95 — 3)/(1.5 — 1)
H = (.95)/(.5) = 1.9Q = (1.25,3.49): H = (3.49 — 3)/(1.25 — 1)
H = (.49)/(.25) = 1.96 -
5
Estimate the slope for an infinitely small interval on the line. As Q gets closer and closer to P, H will get closer and closer to the slope at point P. Eventually, at an infinitely small interval, H will equal the slope at P. Because we aren’t able to measure or calculate an infinitely small interval, we just estimate the slope at P once it’s clear from the points we’ve tried.[8]
- In our example, as we moved Q closer to P, we got values of 1.8, 1.9, and 1.96 for H. Since these numbers appear to be approaching 2, we can say that 2 is a good estimate for the slope at P.
- Remember that the slope at a given point on a line is equal to the derivative of the line’s equation at that point. Since our line is showing our object’s displacement over time and, as we saw in the section above, an object’s instantaneous velocity is the derivative of its displacement at a given point, we can also say that 2 meters/second is a good estimate for the instantaneous velocity at t = 1.
Advertisement
-
1
Find the instantaneous velocity at t = 4 given the displacement equation s = 5t3 — 3t2 + 2t + 9. This is just like our example in the first section, except that we’re dealing with a cubic equation rather than a quadratic equation, so we can solve it in the same way.
- First, we’ll take our equation’s derivative:
s = 5t3 — 3t2 + 2t + 9
s = (3)5t(3 — 1) — (2)3t(2 — 1) + (1)2t(1 — 1) + (0)9t0 — 1
15t(2) — 6t(1) + 2t(0)
15t(2) — 6t + 2 - Then, we’ll plug in our value for t (4):
s = 15t(2) — 6t + 2
15(4)(2) — 6(4) + 2
15(16) — 6(4) + 2
240 — 24 + 2 = 218 meters/second
- First, we’ll take our equation’s derivative:
-
2
Use graphical estimation to find the instantaneous velocity at (1,3) for the displacement equation s = 4t2 — t. For this problem, we’ll use (1,3) as our P point, but we’ll have to find a few other points near it to use as our Q points. Then, it’s just a matter of finding our H values and making an estimation.
- First, let’s find Q points at t = 2, 1.5, 1.1 and 1.01.
s = 4t2 — t
t = 2: s = 4(2)2 — (2)
4(4) — 2 = 16 — 2 = 14, so Q = (2,14)t = 1.5: s = 4(1.5)2 — (1.5)
4(2.25) — 1.5 = 9 — 1.5 = 7.5, so Q = (1.5,7.5)t = 1.1: s = 4(1.1)2 — (1.1)
4(1.21) — 1.1 = 4.84 — 1.1 = 3.74, so Q = (1.1,3.74)t = 1.01: s = 4(1.01)2 — (1.01)
4(1.0201) — 1.01 = 4.0804 — 1.01 = 3.0704, so Q = (1.01,3.0704) - Next, let’s get our H values:
Q = (2,14): H = (14 — 3)/(2 — 1)
H = (11)/(1) = 11Q = (1.5,7.5): H = (7.5 — 3)/(1.5 — 1)
H = (4.5)/(.5) = 9Q = (1.1,3.74): H = (3.74 — 3)/(1.1 — 1)
H = (.74)/(.1) = 7.3Q = (1.01,3.0704): H = (3.0704 — 3)/(1.01 — 1)
H = (.0704)/(.01) = 7.04 - Since our H values seem to be getting very close to 7, we can say that 7 meters/second is a good estimate for the instantaneous velocity at (1,3).
- First, let’s find Q points at t = 2, 1.5, 1.1 and 1.01.
Advertisement
Add New Question
-
Question
What is the difference between instantaneous and average velocity?
Instantaneous is at that moment, whereas average is the mean of the entire time span.
-
Question
How do I calculate instantaneous acceleration?
Instantaneous acceleration can be considered as the value of the derivative of the instantaneous velocity. For example:
s = 5(t^3) — 3(t^2) + 2t + 9
v = 15(t^2) — 6t + 2
a = 30t — 6If we want to know the instantaneous acceleration at t = 4, then a(4) = 30 * 4 — 6 = 114 m/(s^2)
-
Question
When is instantaneous velocity and average velocity the same?
Instantaneous velocity tells you the velocity of an object at a single moment in time. If the object is moving with a constant velocity, then the average velocity and instantaneous velocity will be the same. In all situations, they are not likely to be the same.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
To find acceleration (the change in velocity over time), use the method in part one to get a derivative equation for your displacement function. Then, take another derivative, this time of your derivative equation. This will give you an equation for finding acceleration at a given time — all you have to do is plug in your value for time.
-
The equation which relates Y (displacement) to X (time) might be really simple, like, for instance, Y= 6x + 3. In this case the slope is constant and it is not necessary to find a derivative to find the slope, which is, following the Y = mx + b basic model for linear graphs, 6.
-
Displacement is like distance but it has a set direction, this makes displacement a vector and speed a scalar. Displacement can be negative while distance will only be positive.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To calculate instantaneous velocity, start with an equation for velocity in terms of displacement, which should have an «s» on one side for displacement and a «t» on the other for time. Then, take the equation’s derivative and replace the «s» with the notation «ds» over «dt.» Finally, plug in a «t» value and solve the equation to find the instantaneous velocity at any point in time. To learn how to estimate instantaneous velocity graphically, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,051,180 times.
Did this article help you?
Загрузить PDF
Загрузить PDF
Скорость — это векторная величина, которая характеризует быстроту перемещения и направление движения предмета (тела). В математике скорость определяется как изменение положения тела в зависимости от изменения времени.[1]
Скорость можно найти во множестве физических и математических задач. Выбор правильной формулы зависит от данных значений, поэтому внимательно читайте условие задачи.
Формулы
-
1
-
2
Запишите формулу, содержащую положение и время. Скорость можно вычислить по изменению положения тела и времени. Такую формулу можно применить к любой задаче. Обратите внимание, что если скорость тела меняется, вы найдете среднюю скорость за все время движения, а не конкретную скорость в определенный момент времени.
-
3
Вычислите расстояние между начальным и конечным положениями. То есть между точками начала и окончания движения; они, наряду с направлением движения, указывают на «перемещение» или «изменение положения».[3]
При этом траектория движения тела между этими точками значения не имеет.-
Пример 1: автомобиль, едущий на восток, начинает движение в положении x = 5 м. Через 8 с машина находится в положении х = 41 м. Каково перемещение автомобиля?
- Автомобиль переместился на 41-5 = 36 м на восток.
-
Пример 2: трамплин подбрасывает пловца на 1 метр вверх, и пловец летит до воды 5 м. Каково перемещение пловца?
- Пловец оказался на 4 м ниже начальной точки, поэтому его перемещение равно -4 м (0 + 1 — 5 = -4). Несмотря на то, что пройденное пловцом расстояние составило 6 м (1 м вверх и 5 м вниз), конечная точка находится на 4 м ниже начальной точки.
-
Пример 1: автомобиль, едущий на восток, начинает движение в положении x = 5 м. Через 8 с машина находится в положении х = 41 м. Каково перемещение автомобиля?
-
4
Вычислите изменение времени. Время, которое потребовалось для достижения конечной точки, будет, скорее всего, дано в задаче; если нет, просто вычтите начальное время из конечного.
- Пример 1 (продолжение): в задаче сказано, что машине потребовалось 8 с, чтобы переместиться из начальной точки в конечную, поэтому изменение времени равно 8 с.
- Пример 2 (продолжение): если пловец прыгнул в момент времени t = 7 с и коснулся воды в момент времени t = 8 с, изменение времени: 8 — 7 = 1 с.
-
5
Разделите перемещение на изменение времени. Сделайте это, чтобы найти скорость движущегося тела. Теперь укажите направление движения, и вы получите среднюю скорость.
-
6
Решите задачу, когда направление движения меняется. Не во всех задачах тело движется вдоль одной линии. Если тело совершило поворот, нарисуйте схему движения и решите геометрическую задачу, чтобы найти расстояние.
-
Пример 3: человек бежит 3 м на восток, затем поворачивает на 90° и бежит 4 м на север. Каково перемещение человека?
- Нарисуйте схему и соедините начальную и конечную точки прямой линией. Это гипотенуза треугольника, которую можно найти с помощью теоремы Пифагора или других формул. В нашем примере перемещение составит 5 м на северо-восток.
- Возможно, учитель математики попросит вас найти точное направление движения (в виде угла над горизонтальной прямой). В этом случае воспользуйтесь геометрическими законами или векторами.[4]
Реклама
-
Пример 3: человек бежит 3 м на восток, затем поворачивает на 90° и бежит 4 м на север. Каково перемещение человека?
-
1
Запомните формулу для вычисления скорости ускоряющегося тела. Ускорение — это быстрота изменения скорости. Если ускорение постоянное, скорость меняется с одинаковой быстротой.[5]
Формула включает произведение ускорения и времени, а также начальную скорость: -
2
Умножьте ускорение на изменение времени. Так вы вычислите, насколько скорость увеличилась (или уменьшилась) за это время.
-
Пример: лодка, плывущая на север со скоростью 2 м/с, ускоряется на 10 м/с2. Насколько увеличится скорость лодки в течение 5 с?
- a = 10 м/с 2
- t = 5 с
- (a * t) = 10 * 5 = 50 м/с.
-
Пример: лодка, плывущая на север со скоростью 2 м/с, ускоряется на 10 м/с2. Насколько увеличится скорость лодки в течение 5 с?
-
3
Прибавьте начальную скорость. Вы нашли общее изменение скорости. Прибавьте это значение к начальной скорости тела, чтобы вычислить конечную скорость.
- Пример (продолжение): какова скорость лодки через 5 с?
-
4
Укажите направление движения. Помните, что скорость является векторной величиной, то есть имеет направление. Поэтому в ответе укажите направление.
- В нашем примере лодка начала движение на север и не изменила направление, поэтому ее конечная скорость равна 52 м/с на север.
-
5
Используйте данную формулу, чтобы вычислить другие величины, которые входят в нее. Если известны ускорение и скорость в определенный момент времени, с помощью формулы можно найти скорость в другой момент времени. Например, вычислим начальную скорость:
- Поезд ускоряется на 7 м/с2 в течение 4 секунд и достигает скорости 35 м/с. Какова начальная скорость поезда?
Реклама
-
1
Запомните формулу для вычисления круговой скорости. Круговая скорость — это скорость, которую должно иметь тело, чтобы постоянно вращаться вокруг другого тела, обладающего гравитацией, например, планеты.[6]
- Круговая скорость равна отношению длины круглого пути к периоду времени, в течение которого тело движется.
- Формула для вычисления круговой скорости:
- v = (2πr) / T
- Обратите внимание, что 2πr — это длина окружности.
- r — радиус.
- T — период времени.
-
2
Умножьте радиус окружности на 2π. Сначала необходимо вычислить длину окружности. Для этого умножьте радиус на 2π. В качестве значения π можно использовать 3, 14.
- Пример: найдите круговую скорость тела, движущегося по круговой траектории с радиусом 8 м в течение 45 с.
- r = 8 м
- T = 45 с
- Длина окружности = 2πr ≈ (2)(3,14)(8) = 50,24 м
- Пример: найдите круговую скорость тела, движущегося по круговой траектории с радиусом 8 м в течение 45 с.
-
3
Разделите полученное значение на время. Сделайте это, чтобы вычислить круговую скорость тела.
- Пример: v = (2πr) / T = 50,24 / 45 = 1,12 м/с
- Круговая скорость тела равна 1,12 м/с.
Реклама
- Пример: v = (2πr) / T = 50,24 / 45 = 1,12 м/с
Советы
- Метры в секунду (м/с) — это единица измерения скорости.[7]
. Перед решением задачи убедитесь, что все единицы измерения соответствуют друг другу, например, значения даны в метрах (м), секундах (с), метрах в секунду (м/с) и метрах в квадратных секундах (м/с2). - Средняя скорость характеризует среднюю скорость, которую имеет тело на протяжении всего пути. Мгновенная скорость — это скорость тела в определенный момент времени.
Реклама
Об этой статье
Эту страницу просматривали 17 804 раза.
Была ли эта статья полезной?
Мгновенная скорость, теория и онлайн калькуляторы
Мгновенная скорость
Мгновенная скорость при прямолинейном движении материальной точки
При рассмотрении неравномерного движения часто интересует не средняя скорость движения тела, а скорость в определенный момент времени, или мгновенная скорость. Так, если тело стукнулось о препятствие, то сила воздействия тела на препятствие в момент удара, определено скоростью в момент соударения, а не средней скоростью движения тела. Форма траектории перемещения снаряда и его дальность полета зависит от скорости в момент запуска, а не от средней скорости.
Средняя скорость ($leftlangle vrightrangle $) движения материальной точки по оси X равна:
[leftlangle vrightrangle =frac{Delta x}{Delta t}left(1right),]
$Delta t$ — промежуток времени движения тела.
Определение
Мгновенную скорость определим как предел к которому стремится средняя скорость за бесконечно малый промежуток времени:
[v={mathop{lim }_{Delta tto 0} leftlangle vrightrangle }={mathop{lim }_{Delta tto 0} frac{Delta x}{Delta t}left(2right). }]
Такой предел в математике называют производной:
[v=frac{dx}{dt}=dot{x}left(3right).]
Выражение (3) обозначает, что мгновенная скорость (скорость в определенный момент времени) — производная от координаты. При прямолинейном движении материальной точки Мгновенную скорость можно определить как производную от пути ($s$) по времени:
[v=frac{ds}{dt}=dot{s}left(4right).]
Мгновенная скорость равномерного движения материальной точки
Средняя скорость равномерно движущейся точки величина постоянная, значит, мгновенная скорость равномерно перемещающейся точки является неизменной величиной.
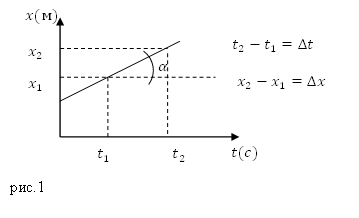
Скорость равномерного движения численно равна тангенсу угла наклона прямой к оси времени (рис.1):
[v=k tg alpha left(4right),]
где $k$ — безразмерный коэффициент, определяющий отношение масштаба единиц перемещения (ось ординат) и единиц времени (ось абсцисс).
При графическом изображении переменного движения материальной точки мгновенная скорость численно равна тангенсу угла наклона касательной к графику и осью абсцисс.
Мгновенная скорость при криволинейном движении
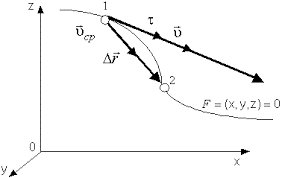
Положение материальной точки на траектории зададим радиус-вектором $overline{r}(t)$, который проведем в точку наблюдения из какой-либо неподвижной точки, которую примем за начало координат. Тогда мгновенной скоростью материальной точки будет векторная величина, равная:
[overline{v}=frac{doverline{r}}{dt}=dot{overline{r}}left(5right).]
скорость — это вектор, направленный по касательной к траектории движения материальной точки в месте нахождения частицы.
Примеры задач с решением
Пример 1
Задание. Две материальные точки движутся согласно уравнениям:
[left{ begin{array}{c}
x_1=-3t+4t^2-t^3(м) \
x_2=t-2t^2-t^3(м) end{array}
right.left(1.1right),]
в какой момент времени скорости этих точек будут равны?
Решение. В задаче речь идет о нахождении времени, когда будут равны мгновенные скорости материальных точек. Величину мгновенной скорости будем находить как:
[v=frac{dx}{dt}left(1.2right).]
Тогда подставляя по очереди уравнения из системы (1.1) получим:
[left{ begin{array}{c}
v_1=frac{dx_1}{dt}=-3+8t-3t^2 \
v_2=frac{dx_2}{dt}=1-4t-3t^2 end{array}
right.left(1.3right).]
Приравняем правые части уравнений в системе (1.3), найдем момент времени в который скорости равны ($v_1=v_2$):
[-3+8t-3t^2=1-4t-3t^2to 8t+4t=1+3to 12t=4to t=frac{1}{3}left(cright).]
Ответ. $t=frac{1}{3}$ с
Пример 2
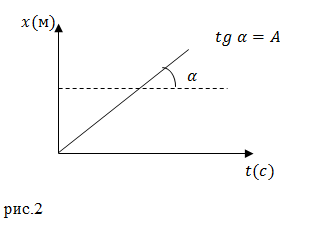
Задание. Материальная точка движется на плоскости XOY. Закон изменения координаты $x$ задан графиком рис.2 . Координата $y $задана аналитическим выражением: $y=At(1+Bt)$, где $A$ и $B$ постоянные величины. Запишите выражение, связывающее мгновенную скорость и время ($v(t)$).
Решение. Из рис. 2 мы можем записать уравнение, которое определяет изменение координаты $x$ от времени:
[xleft(tright)=At left(2.1right).]
Получили, что движение материальной точки в плоскости XOY описывают при помощи системы уравнений:
[left{ begin{array}{c}
xleft(tright)=At;; \
y=Atleft(1+Btright) end{array}
left(2.2right).right.]
Найдем составляющие скорости движения материальной точки:
[v_x=frac{dx}{dt}=frac{d}{dt}left(Atright)=A;;]
[v_y=frac{dy}{dt}=frac{d}{dt}left(Atleft(1+Btright)right)=A+2ABt.]
Модуль скорости найдем как:
[v=sqrt{v^2_x+v^2_y}=sqrt{A^2+{(A+2ABt)}^2}=sqrt{A^2+A^2+2A^2Bt+4A^2B^2t^2}=]
[=Asqrt{2+2Bt+4B^2t^2.}]
Ответ. $v=Asqrt{2+2Bt+4B^2t^2}$
Читать дальше: механические волны.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Определение
Скорость — это термин, который характеризует изменение заданной координаты в движении.
В ситуации, когда координаты изменяют свое положение относительно оси, следовательно, их материальная точка будет находится в процессе движения.
Средняя скорость — это величина векторного типа, которая имеет определенное числовое равенство относительно перемещения совершаемого в конкретную единицу времени, и направлена совместно я с векторным перемещением.
Средняя скорость – довольно простое понятие в разделе кинематика.
Определение
Следовательно, средняя скорость – это конкретная величина, которая равна отношению пройденного пути, к величине времени, за которое данный путь пройден телом.
[v_{mathrm{cp}}=frac{S}{t}]
Основные моменты, на которые следует уделить внимание при определении средней скорости:
- Необходимое время, которое учитывается, когда тело в процессе движения может делать кратковременные остановки;
- Определение правильной величины средней скорость тела, которое начинает движение в пункте А и оканчивает его в пункте В. Но в процессе движения, может повернуть несколько раз обратно, а затем снова продолжает движение в заданном направлении, двигаясь в пункт В.
Модуль для определения средней скорости движения вычисляется по следующей формуле: V=s/t.
Определение
Мгновенная скорость — это некий числовой предел, к которому стремится показатель средней скорости.
Мгновенная скорость, как правило, характеризует заданное движение точки в конкретный и определенный момент времени.
Для любой категории характерно бесконечное количество точек. Потому что каждый временной интервал включает в себя бесконечное количество мгновений.
Когда сам временной интервал стремится к нулевому значению, то он автоматически преобразуется в мгновение.
Формула
Мгновение скорости можно определить по следующей формуле: v=s/Δt
где:
v – скорость мгновения, м/с
s – движение, перемещение тела, м ( если Δt→0 )
Δt – временной интервал, который стремится к нулевому значению, с.
Стоит отметить, что мгновенная скорость – это величина, которая изображена как вектор. Она равняется отношению движения к временному интервалу. А именно: промежуток времени, за который данное перемещение происходит, при условии, что временной интервал стремится к нулевому значению.
Временной интервал движения тела – это всегда скляр с положительным значением. Поэтому мгновенная скорость и ее векторное значение, всегда сонаправлено с перемещением, которое имеет значение стремящееся к нулю.
Нет времени решать самому?
Наши эксперты помогут!
Направление и перемещение действия средней и мгновенной скорости относительно координатной оси
Средняя скорость всегда направлена вместе с перемещением:
Для мгновенной скорости характерно движение в конкретный момент времени.
Направление векторной скорости, которая обозначается как: υ расположено по касательной, относительно криволинейной траектории.
Так как непрерывное малое перемещение однозначно совпадает с бесконечно малым элементом траектории.
Примеры решения задач по определению мгновенной и средней скорости
Пример №1:
Имеет ли способность мгновенная скорость, изменять свое значение только относительно направления, при этом не меняя модульную величину.
Используя основные термины и формулы, решим данную задачу. При решении необходимо рассмотреть пример:
- Движение тела происходит по криволинейной траектории. На ней необходимо обозначить начальный и конечный пункты, а именно: точки А и В.
- Далее нужно обозначить основное направление мгновенной скорости в заданных ранее точках.
- Следует помнить, что мгновенная скорость имеет направление относительно касательной по траектории.
- Расстояние и скорость имеют одинаковые значения по модулю и, следовательно, равны 5 м/с.
[left|vec{V}_{A}right|=left|vec{V}_{B}right|=5 frac{м}{c}]
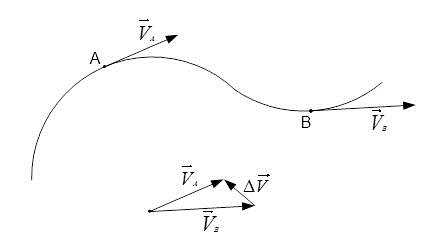
Следующее равенство вида: [vec{V}_{A}=vec{V}_{B}] будет неверным. Так как скорость – является векторной величиной. Поэтому очень важно задать не только числовое значение, но направление по которому будет осуществляться движение.
В случае, когда [vec{V}_{A}=vec{V}_{B}] можно составить равенство следующего вида:[vec{V}_{A}-vec{V}_{B}=0] однако определив вектор разности значений [Delta vec{V}], можно сделать вывод, что его значение не равно нулевому.
Следовательно, [vec{V}_{A} neq vec{V}_{B}], другими словами мгновенная скорость может быть равна нулевому значению и быть равной по модулю. Однако, при этом различаться по основному направлению движения.
Пример №2:
Возможно ли изменение по модульному значению мгновенной скорости, но при этом направление остается неизменным.
Алгоритм решения:
Рассмотрев рисунок, который приведен выше, можно сделать вывод, что:
- в точке А и в точке В направление движения мгновенной скорости одинаково;
- рассматриваемое тело, которое осуществляет движение, делает это с равным ускорением, следовательно:
[vec{V}_{A}=vec{V}_{B}]
При движении материальной точки изменяются ее координаты. Координаты могут изменяться быстро или медленно. Физическая величина, которая характеризует быстроту изменения координаты, называется скоростью.
Mодуль средней скорости по пути равен: $leftlangle vrightrangle =frac{S}{triangle t}$
Мгновенная скорость дает точную информацию о движении в определенный момент времени. Выражение «скорость тела в данный момент времени» с точки зрения физики не является корректным. Однако понятие мгновенной скорости очень удобно в математических расчетах, и им постоянно пользуются.
Мгновенная скорость (или просто скорость) есть предел, к которому стремится средняя скорость $leftlangle vrightrangle $ при стремлении промежутка времени $triangle t$ к нулю:
$v={mathop{lim}_{triangle t} frac{triangle r}{triangle t} }=frac{dr}{dt}=dot{r}$ (1)
Вектор $v$ направлен по касательной к криволинейной траектории, так как бесконечно малое (элементарное) перемещение dr совпадает с бесконечно малым элементом траектории ds.
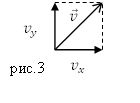
Рисунок 2. Вектор мгновенной скорости $v$
В декартовых координатах уравнение (1) эквивалентно трем уравнениям
$left{ begin{array}{c}
v_x=frac{dx}{dt}=dot{x} \
v_y=frac{dy}{dt}=dot{y} \
v_z=frac{dz}{dt}=dot{z} end{array}
right.$ (2)
Модуль вектора $v$ в этом случае равен:
$v=left|vright|=sqrt{v^2_x+v^2_y+v^2_z}=sqrt{x^2+y^2+z^2}$ (3)
Переход от декартовых прямоугольных координат к криволинейным осуществляется по правилам дифференцирования сложных функций. Пусть радиус-вектор r есть функция криволинейных координат: $r=rleft(q_1,q_2,q_3right) $. Тогда скорость $v=frac{dr}{dt}=sum^3_{i=1}{frac{partial r}{partial q_i}frac{partial q_i}{partial t}}=sum^3_{i=1}{frac{partial r}{partial q_i}}dot{q_i}$
Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат
В сферических координатах, полагая $q_1=r; q_2=varphi ; q_3=theta $, получаем представление $v$ в следующий форме:
$v=v_re_r+v_{varphi }e_{varphi }+v_{theta }e_{theta }$, где $v_r=dot{r}; v_{varphi }=rdot{varphi }sintheta ;; v_{theta }=rdot{theta } ;;$
[dot{r}=frac{dr}{dt};; dot{varphi }=frac{dvarphi }{dt};; dot{theta }=frac{dtheta }{dt}; v=rsqrt{1+{varphi }^2sin^2theta +{theta }^2}]
Мгновенная скорость — это значение производной от функции перемещения по времени в заданный момент времени, и связана с элементарным перемещением следующим соотношением: $dr=vleft(tright)dt$