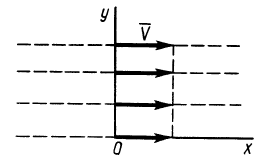
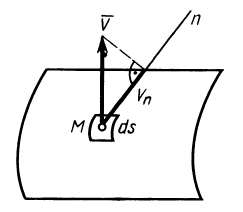
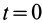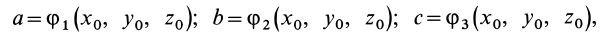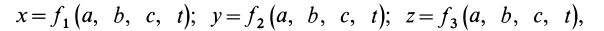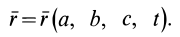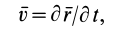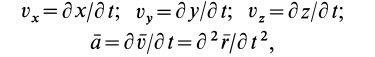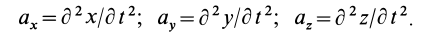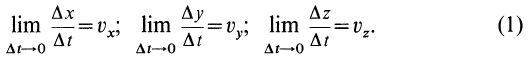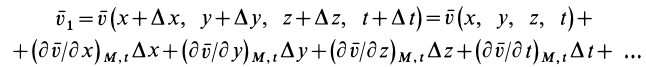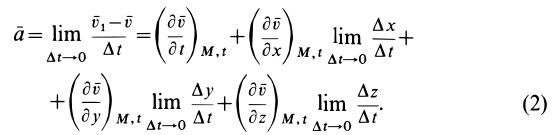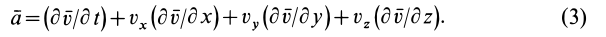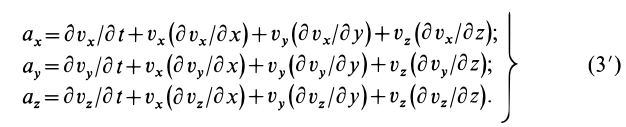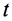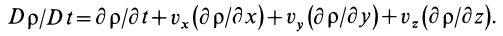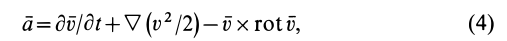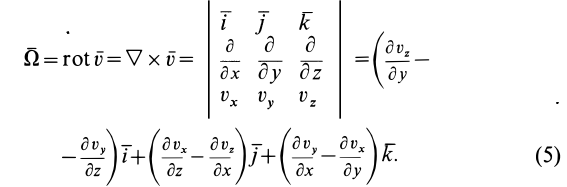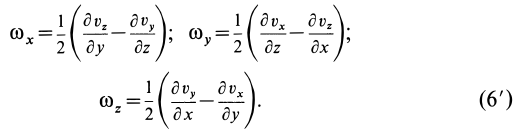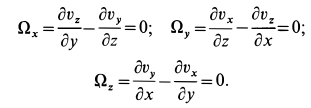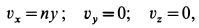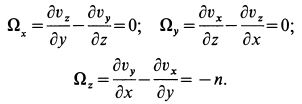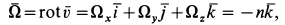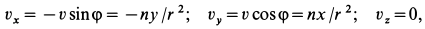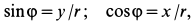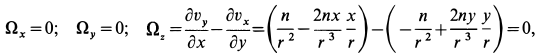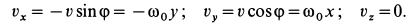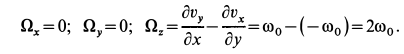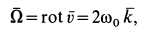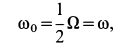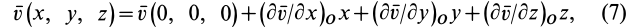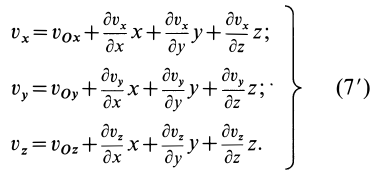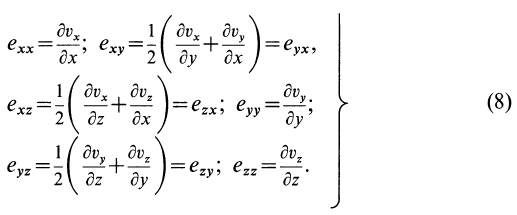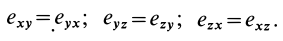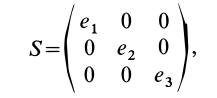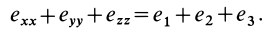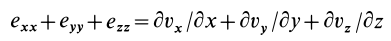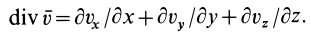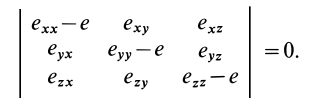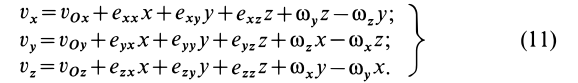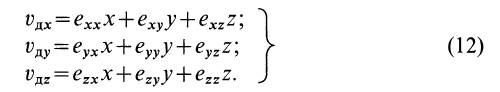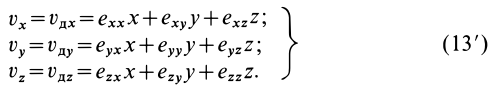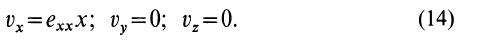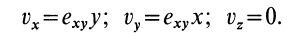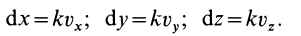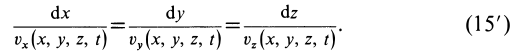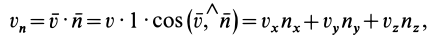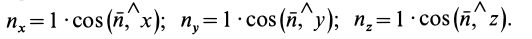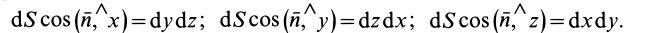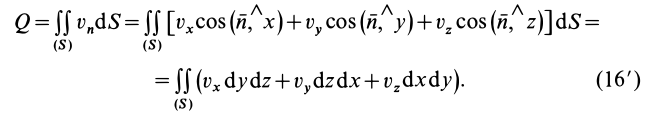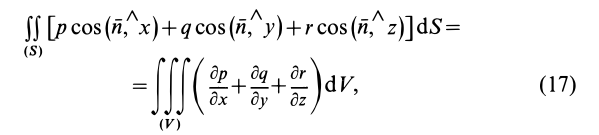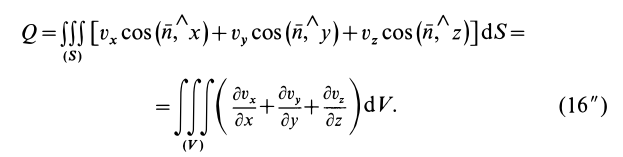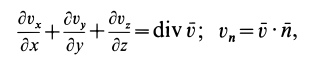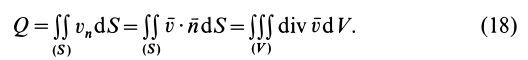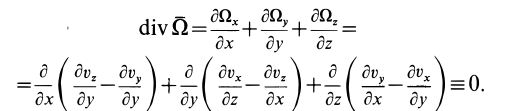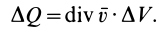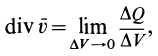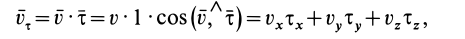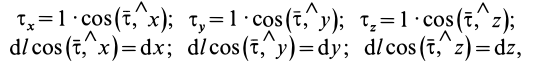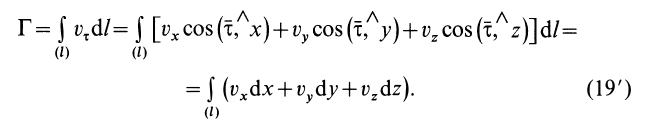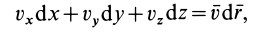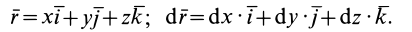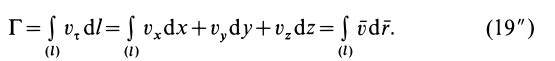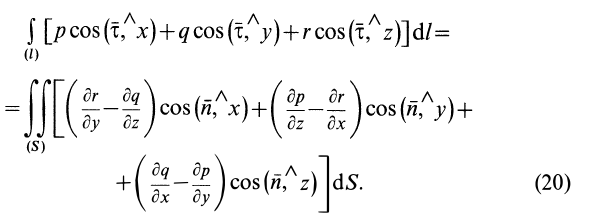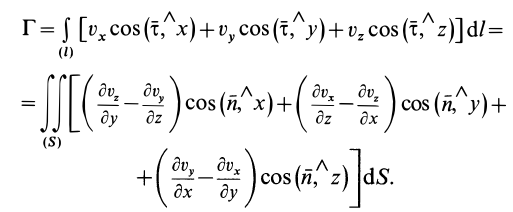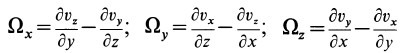Содержание:
Основы кинематики сплошной среды:
Сплошной средой считают деформируемые тела, различные жидкости, не очень разреженные газы. Понятия скорости и ускорения точки сплошной среды такие же, как и в кинематике одной точки. В кинематике сплошной среды роль точки отводится малой частице этой среды. Рассмотрим задания движения сплошной среды и получим формулы, по которым вычисляются скорости и ускорения точек сплошной среды.
Движение сплошной среды может быть изучено двумя методами, один из которых — метод Лагранжа — является обобщением метода, применявшегося в кинематике одной точки. Движение в методе Лагранжа задается в переменных Лагранжа. Другой метод — метод Эйлера — широко использует концепцию теории поля. При этом движение задается и изучается в переменных Эйлера. При рассмотрении движения сплошной среды преимущественно используется полевой подход, базирующийся на методе Эйлера и соответственно использующий переменные Эйлера.
Переменные Лагранжа
В выделенном объеме сплошной среды каждая его точка (малая частица) в фиксированный момент времени, например
допускающими вторые производные по всем переменным. Параметры 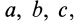
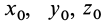
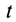
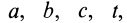
Для задания движения сплошной среды в переменных Лагранжа, как и в случае одной точки, достаточно задать декартовы координаты 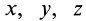
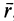
или
В кинематике одной точки, которая рассматривалась ранее, использовались переменные Лагранжа для этой точки. Параметры 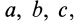
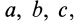
Если движение сплошной среды задано в переменных Лагранжа, то скорости и ускорения в этих переменных определяются по обычным формулам кинематики точки:
или
или
Производные по времени 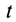
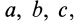
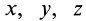
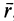
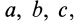
В методе Лагранжа объектом изучения являются сами точки движущейся сплошной среды.
Переменные Эйлера
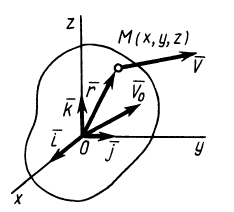
В механике сплошной среды, особенно для жидкостей и газов, а также в теории поля преимущественно используются метод Эйлера и соответственно переменные Эйлера. В методе Эйлера рассматриваются не фиксированные точки сплошной среды, а точки пространства, занятые движущейся сплошной средой. За независимые переменные принимают время 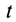
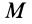
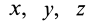
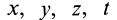
Различные векторные и скалярные величины, характеризующие сплошную среду, такие, как, например, скорость, ускорение, плотность и т. п., рассматривают как функции этих переменных. В случае сплошной среды изучаются поля скалярных и векторных величин, характеризующих движущуюся сплошную среду и ее свойства. Изучаются распределение этих величин по точкам пространства, занятого сплошной средой, и их изменение с течением времени.
По известному векторному полю скоростей сплошной среды, заданному в переменных Эйлера 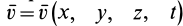
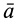
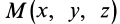
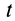
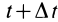
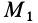
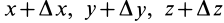
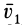
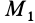
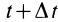
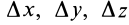
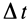
Разложим скорость 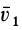
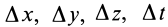
Индексы 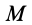
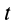
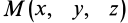
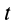
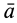
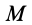
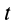
Остальные слагаемые ряда в пределе обращаются в ноль. Подставляя (1) в (2) и опуская для краткости индексы 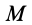
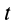
В проекциях на координатные оси имеем
По векторной формуле (3) вычисляют поле ускорений в переменных Эйлера, если известно поле скоростей. В эту формулу входят 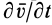
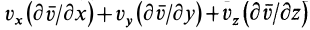
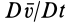
Локальная производная 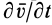
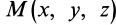
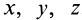
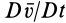
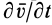
Группа слагаемых, представляющая конвективную производную, учитывает изменение вектора скорости, вызванное переносом рассматриваемой точки сплошной среды самой движущейся средой.
Рассмотрим частные случаи
1. Если 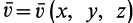
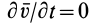
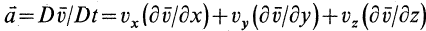
2. При 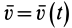
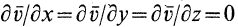
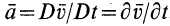
3. Если 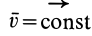
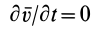
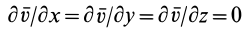
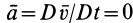
По формуле (3) вычисляют полные, или субстанциальные, производные по времени в переменных Эйлера от любых векторных или скалярных величин, характеризующих сплошную среду. Пусть, например, известно скалярное поле плотностей 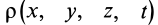
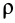
Если сплошная среда неподвижна, т. е. 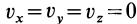
Преобразованием конвективной производной из (3) можно получить другое выражение для ускорения (формула Лэмба — Громеко):
где 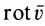

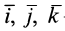
В дальнейшем используется также вектор 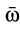
В проекциях на оси координат
Для выяснения физического смысла 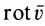
Пример 1.
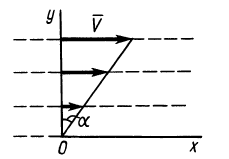
Сплошная среда совершает плоское движение, параллельное оси 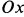
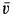
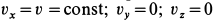
По формуле (5) для вектора вихря 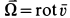
Рис. 104
Рис. 105
Рис. 106
Рис. 107
Следовательно, 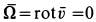
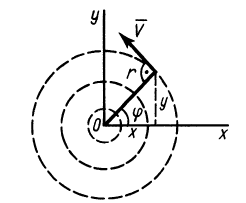
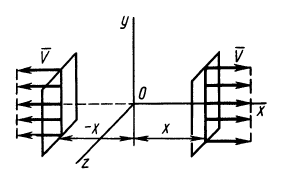
Пример 2.
Сплошная среда совершает плоское движение, параллельное оси 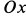
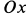
где 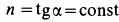
Таким образом, во всех точках потока сплошной среды
где 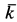
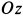
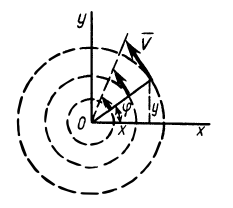
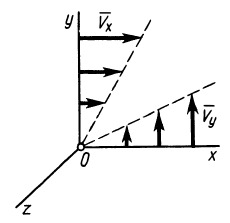
Пример 3.
Точки сплошной среды движутся по круговым траекториям с центрами на оси 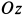
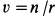
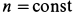
так как
где 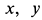
так как 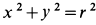
Следовательно, 
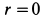
Пример 4.
Сплошная среда вращается как твердое тело вокруг неподвижной оси 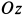
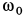
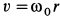
По формулам для вихря скорости имеем
Следовательно,
де 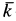
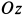

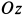

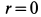
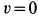
Угловая скорость
т. е. равна половине вихря вектора скорости. Таким образом, половина вихря вектора скорости является вектором угловой скорости вращения твердого тела вокруг неподвижной оси.
Распределение скоростей в малой окрестности точки пространства
Пусть известны скорость в точке 
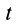
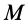

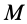


Точки 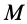

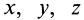
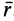
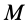
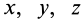
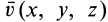
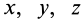
где 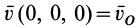



Рис. 108
Введем компоненты тензора скоростей деформации 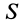

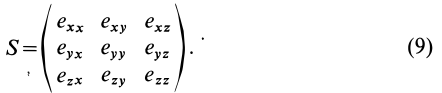
Тензор скоростей деформаций удобно представить в форме таблицы или матрицы:
Компоненты тензора скоростей деформаций, характеризующие движение сплошной среды, зависят от точки пространства и направления осей координат. Тензор 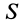
Для таких симметричных тензоров в линейной алгебре доказывается, что в каждой точке существуют такие прямоугольные оси координат, называемые главными осями, для которых тензор принимает диагональную форму:
где 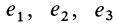
Скалярная величина
называется дивергенцией (расхождением) вектора скорости и обозначается 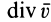
Величины 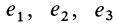
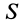
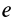
Известно, что числу соответствует геометрический образ, которым является точка на числовой оси. Вектору соответствует прямолинейный отрезок. Тензору 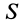
Применим для производных по координатам от проекций вектора скорости на оси координат тождественные преобразования Коши, прибавляя и вычитая одинаковые величины и используя (6′) и (8). Имеем
Из (7′) с учетом этих преобразований получаем
В векторной форме (11) примет вид
где 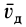
По формуле (11′) вычисляется скорость в момент времени 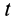
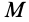
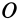
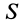
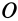
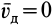
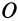
Рассмотрим скорость деформации 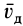
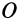
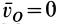
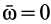
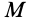
или в проекциях на оси координат
Если в точке 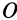
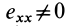
Из (14) следует, что точки сплошной среды из малой окрестности точки 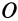
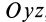
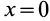
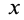
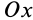
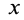
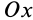
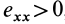
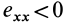
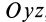
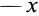
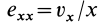
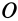
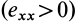
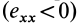
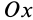
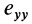
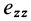
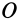
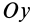
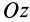
Допустим, что 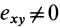
Рис. 109
Рис. 110
Это показывает, что точки сплошной среды из малой окрестности точки 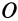
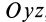
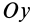
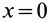
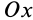
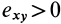
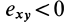
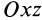
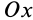
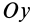
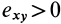
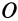
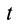
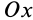
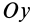
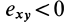
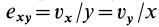
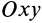
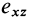
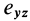
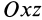
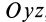
В общем случае, если все компоненты тензора скоростей деформации отличны от нуля, рассмотренные эффекты в окрестности точки 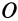
- Заказать решение задач по теоретической механике
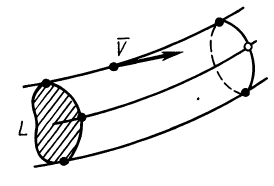
Линии и трубки тока
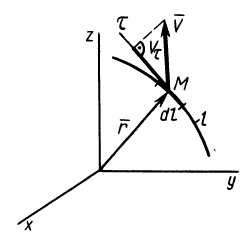
При рассмотрении движения сплошной среды и применении переменных Эйлера используется понятие линий тока, т. е. линий, в каждой точке которых в рассматриваемый момент времени векторы скоростей параллельны касательным этих линий. Если вектор в какой-либо точке линии тока направлен по касательной к этой линии, то, по определению линии тока, он должен быть параллельным вектору скорости 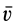
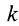
Рис. 111
Если проекции вектора 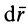
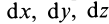
Отбрасывая произвольный множитель 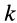
Два уравнения (15′) относительно координат 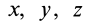
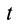
Линии тока являются векторными линиями для векторного поля скоростей точек сплошной среды. Аналогичные векторные линии можно получить для любого другого векторного поля, например векторного поля вихря вектора скорости и т. п.
Если выбрать в пространстве, в котором движется сплошная среда, какой-либо замкнутый контур 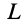
Поток и циркуляция вектора скорости
Поток вектора скорости: Выберем в пространстве, в котором движется сплошная среда, неподвижную поверхность относительно рассматриваемой системы отсчета. Разобьем ее на малые элементарные площадки с площадью 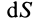
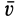
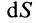
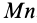
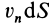
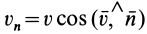
Рис. 112
Для замкнутой поверхности внешней нормалью в каждой ее точке называют нормаль, которая направлена во внешнюю часть объема, ограниченного поверхностью. Для незамкнутых поверхностей дополнительно уславливаются, какое направление нормали считать внешним.
Потоком 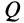
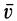
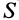
Для вычисления потока можно получить другие выражения, если учесть, что
где 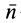
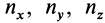
Кроме того,
После этого для потока получаем
Наиболее часто используемое выражение для потока получают применением формулы Гаусса—Остроградского для преобразования интеграла по замкнутой поверхности 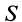
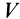
где 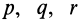
Если принять 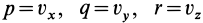
Ho
поэтому
Для вектора вихря скорости поток через замкнутую поверхность равен нулю, так как с учетом формул для проекций вектора вихря на координатные оси имеем
Из (18) для потока 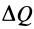
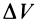
Отсюда получаем для дивергенции вектора скорости
т. е. дивергенцию вектора скорости в какой-либо точке можно рассматривать как предел потока вектора скорости через замкнутую поверхность, приходящуюся на единицу объема, ограниченного поверхностью, при стягивании объема в эту точку.
Рис. 113
Циркуляция вектора скорости: Для введения понятия циркуляции вектора скорости по какому-либо контуру следует выбрать контур 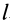
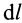
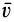
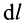
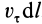
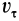
Циркуляция вектора скорости по всему контуру
Для вычисления циркуляции можно получить другие формулы, если учесть, что
где 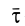
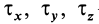
получим
Ho
где 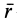
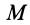
Таким образом,
Для замкнутого контура можно применить формулу Стокса, преобразующую интеграл по контуру в интеграл по поверхности, натянутой на этот контур:
Если принять 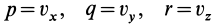
Учитывая, что
являются проекциями вихря скорости, для циркуляции по замкнутому контуру получим
Если 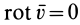
Для вектора силы 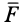
- Аксиомы классической механики
- Дифференциальные уравнения движения материальной точки
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Мгновенный центр вращения
- Вращение твердого тела вокруг неподвижной точки
- Сложное движение точки
- Сложение движение твердого тела
Задача кинематики
описание движения среды независимо от
внешних условий, которые инициируют и
поддерживают движение. Т.к. сплошная
среда представляет собой непрерывную
совокупность точек, то чтобы описать
её движение, необходимо описать движение
всех точек. Поэтому вернёмся к некоторым
понятиям теоретической механики,
изучающей движение точки.
3.1. Движение точки с позиций теоретической механики
Траектория
движущейся точки.
Движение материальной точки мы
рассматриваем в теоретической механике.
В этом случае, для описания полного
движения точки необходимо знать уравнение
её движения т.е.
,
где
радиус-вектор точки. Чтобы найти скорость
точки надо взять производную от правой
части уравнения движения.
Рассмотрим движение
точки в некоторой определённой системе
прямоугольных и прямолинейных координат
Oxyz,
которую условимся называть неподвижной.
Кривая, описываемая
последовательными положениями движущейся
точки, называется траекторией.
Аналитически
движение точки определено, если заданы
её координаты x,
y,
z,
как непрерывные функции времени t:
x
= 1
(t);
y
= 2(t);
z
= 3(t).
Эти уравнения
определяют положение движущейся точки
в каждый момент времени t
и представляют в параметрической форме
уравнение траектории. Если на траектории
выбрать точку М0,
от которой отсчитывать длину дуги s
траектории до движущейся точки М, то
движение М определяется законом изменения
s,
как функции времени t:
s
= s
(t).
Перемещение.
Скорость.
Пусть М и М
положения движущейся точки, отвечающие
соответственно моментам t
и t
+ t.
Вектор
называется перемещением
точки за
промежуток времени t
. Этот вектор с началом в точке М
представляет собой хорду, стягивающую
положения движущейся точки в моменты
t
и t
+ t
.
Перемещение
разделим на t;
вектор
называется средней
скоростью
точки М за промежуток времени t
.
Средняя скорость
есть вектор, приложенный в точке М и
имеющий то же направление, что и
перемещение
.
Предел средней
скорости, когда t
стремится к 0, называется скоростью
точки М в момент t
и обычно обозначается
.
В пределе направление
хорды совпадает с направлением касательной
к траектории; поэтому скорость u
точки М представляет собой вектор,
приложенный в точке М и направленный
по касательной к траектории в сторону
движения.
Положение точки
М можно определить вектором
,
выходящим из начала координат О.
Перемещение
за промежуток времени t
равно приращению
вектора
:
откуда
Таким образом,
скорость движущейся точки равна
производной по времени от радиуса-вектора
движущейся точки и представляет собой
вектор, приложенный в движущейся точке.
Проекции скорости
на оси координат.
Пусть x,
y,
z
координаты точки М, а x
+ x,
y
+y,
z
+z
координаты точки
.
Проекции перемещения
на оси координат будут соответственно
равны x,
y,
z;
проекции средней скорости w
будут
отсюда проекции
истинной скорости u
на оси координат Oxyz
будут пределами предыдущих выражений
при t
0, или
Теорема.
Проекции скорости на прямоугольные оси
равны первым производным по времени от
соответствующих координат движущейся
точки.
Так как оси Oxyz
ортогональны, величина скорости
определится через проекции формулой:
.
Если через s
обозначить длину дуги траектории,
отсчитываемой от неподвижной точки, то
.
Следовательно,
алгебраическая величина скорости будет
определяться формулой
.
При этом, если u
положительна, то скорость направлена
в сторону возрастающих значений s.
Движение называется равномерным, если
величина скорости постоянна. Тогда
Допустим, что s0
есть значение s
для начального момента времени t
= 0; тогда, интегрируя предыдущее выражение,
получаем: s
= s0
+ at.
То есть, в равномерном
движении пройденные пути пропорциональны
времени. Величина скорости равна пути,
пройденному в равномерном движении за
единицу времени.
Теорема о проекции
скорости.
Возьмём ось х за траекторию движения
(если движение прямолинейное). Значит
s
= х, и уравнение движения имеет вид: x
= f(t).
Алгебраическая величина скорости точки,
движущейся по оси х, представляется
формулой
v
= dx/dt
= f(t).
Но, при движении
точки в пространстве, dx/dt
есть проекция её скорости на ось х; в то
же время эта величина равна скорости
ортогональной проекции М1
точки М на ось х, так как х есть абсцисса
точки М1.
Следовательно,
если спроектировать на неподвижную ось
движущуюся точку и её скорость, то
проекция скорости будет равна скорости
проекции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Раздел 1. |
КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ |
Задание движения сплошной среды.
Индивидуальная и местная производные
По определению, знать движение сплошной среды – значит знать движение всех ее точек. Индивидуальные точки сплошной среды можно задавать значениями их начальных координат. Координаты точек в начальные моменты времени t0 будем обозначать: x0, y0, z0, а координаты точек в любой момент времени – x, y, z. Для любой точки, выделенной координатами x0, y0, z0,
можно написать закон движения:
|
x = x (t, x0, y0, z0), |
|
|
y = y (t, x0, y0, z0), |
(1.1) |
|
z = z (t, x0, y0, z0). |
Если в (1.1) x0, y0, z0 – фиксированы, а t – переменно, то мы получим закон движения одной точки среды. Если x0, y0, z0 – переменны, а t – фиксировано, то мы получим распределение точек среды в пространстве в данный момент времени.
Координаты x0, y0, z0 (индивидуализирующие точки среды) и время t
являются переменными Лагранжа.
Предположим теперь, что нас интересует не само движение индивидуальных точек среды, а то, что происходит в разные моменты времени в данной точке пространства. Пусть наше внимание концентрируется на определенной точке пространства, в которую попадают различные частицы сплошной среды. Это составляет суть точки зрения Эйлера на изучение движения среды. Геометрические координаты пространства x, y, z и время t
– переменные Эйлера. Движение среды, по Эйлеру, задается полем скоростей:
|
wx = wx (t, x, y, z), |
|
|
wy = wy (t, x, y, z), |
(1.2) |
|
wz = wz (t, x, y, z) |
(w =i wx +j wy + wz – задание картины поля скоростей).
Если в (1.2) x, y, z – фиксированы, а t – переменно, то мы получим изменение со временем скорости в данной точке пространства для различных частиц, попадающих в эту точку. При фиксированном t и переменных x, y, z
эти функции дают распределение скоростей в определенный момент времени.
Распределение скоростей можно задать с точки зрения как Лагранжа [w (t, x0, y0, z0)], так и Эйлера [w (t, x, y, z)]. Если распределение скорости задано по Лагранжу, то изменение скорости w в единицу времени t частицы среды найти просто. Оно будет равно производной dw / dt.
Как вычислить ту же величину, если распределение скорости задано по Эйлеру: w (t, x, y, z)? Очевидно, что для этого надо перейти от переменных Эйлера к переменным Лагранжа:
w (t, x, y, z) = w t, x (t, x0, y0, z0), y (t, x0, y0, z0), z (t, x0, y0, z0)
–
и воспользоваться правилом дифференцирования сложной функции. Тогда
где x / t; y / t; z / t – производные, берутся при постоянных x0, y0, z0 и,
следовательно, являются компонентами скорости wx, wy, wz.
П
оэтому
Т
аким образом, мы получили выражение вектора ускорения в эйлеровых переменных. Вводя некоторый условный вектор с проекциями
п
редставим (1.3) так:
Производная dw / dt, характеризующая изменение скорости со временем
в данной точке сплошной среды, называется полной, или индивидуальной, или субстанциональной.
Производная w / t, характеризующая изменение скорости в данной точке пространства x, y, z, называется местной, или локальной.
Она характеризует нестационарность среды (если среда стационарна, то
w / t = 0).
Величина (w)w, образующаяся за счет изменения координат точки, соответствующей передвижению (конвекции) ее в поле физической величины, называется конвективной производной. Она характеризует неоднородность поля в данный момент времени.
В
общем случае выражение
можно рассматривать как некий оператор индивидуальной производной. Этот оператор может применяться к скалярным функциям, а также к тензорным величинам, связанным с движущейся частицей.
Линии тока и траектории
Если движение жидкости задано в переменных Лагранжа, то геометрическое представление потока дается траекториями. В переменных Эйлера для геометрической интерпретации потока пользуются линией тока, т. е. такой линией, в каждой точке которой в данный момент времени вектор скорости совпадает с касательной к этой линии. Совпадение не только линий тока для различных моментов времени, но и их траекторий имеет место в случае установившегося, или стационарного, движения. При нестационарном течении линии тока, построенные для различных моментов времени, не будут совпадать как между собой, так и с траекториями. Из определения линии тока следует, что в каждой ее точке нормальная составляющая скорости равна нулю (т. е. через л

Рис.1. Нулевая линия тока
инию тока нет перетекания). Таким образом, между двумя произвольными линиями тока количество текущей жидкости постоянно. Если через поверхность обтекаемого тела жидкость не проходит, то эта поверхность является поверхностью тока. Для плоского обтекания это будет линия тока, которая называется нулевой линией тока (рис. 1).
Т
ак как касательная к линии тока совпадает с вектором скорости, то уравнение линии тока можно записать следующим образом:
где – элемент линии тока; w – скорость;
и
ли
или
В
общем случае через любую точку в данный момент времени можно провести лишь одну линию тока. Но существуют некоторые особые точки, в которых это правило нарушается: в них линии тока пересекаются и, следовательно, вектор скорости должен иметь разные направления, что при конечном значении скорости невозможно. Поэтому в особых точках скорость должна быть равна либо нулю, либо бесконечности. На рис. 1 критическими точками являются А и А1 – в них скорость равна нулю.
Скоростное поле сплошной среды в окрестности точки.
Первая теорема Гельмгольца
Возьмем бесконечно малую частицу сплошной среды и найдем распределение скоростей в этой частице. Под бесконечно малой частицей будем понимать совокупность точек среды с координатами ηi + dηi = ηi + ρi,
у

Рис. 2. Скоростное поле сплошной среды
даленных от центра 0 на бесконечно малые расстояния ρ. Пусть скорость точки 0 есть w 0, а любой точки 01
– w 1 (рис. 2).
Р
ассмотрим разложение скоростей в окрестности точки 0 с точностью до малых первого порядка по (ряд Тейлора). Скорость среды w в окрестности точки является регулярной функцией точки (регулярная функция – это функция без разрывов), что позволяет применить разложение в степенной ряд:
где
У
равнение (1.8) выражает скорость любой точки 01 бесконечно малой частицы сплошной среды через скорость ее центра w0, производные от w по координатам в центре и координаты рассматриваемой точки.
З
апишем уравнение (1.8) в тензорном виде:
где i – оператор Гамильтона; эk – векторы базиса (1 =i; э2 =j; =).
В
ведя сопряженный тензор k wi , запишем предыдущее уравнение в следующем виде:
В
уравнении (1.9) присутствуют члены, содержащие антисимметричный тензор wki и симметричный тензор lki :
Таким образом, скорость точек частицы сплошной среды разбита на три составляющие, первая из которых w0 (wx0 , wy0 , wz0) не зависит от координат и, следовательно, представляет скорость поступательного движения всей частицы. Выясним кинематический смысл остальных составляющих.
Р
ассмотрим вторую составляющую, для которой запишем таблицу антисимметричного тензора:
К
аждый член этой таблицы выглядит следующим образом:
С
учетом (1.11) таблицу можно представить так:
О
тсюда видно, что члены таблицы являются угловыми скоростями вращательного движения частицы сплошной среды относительно начальной точки, т. е. вторая составляющая в (1.9) характеризует вращательное движение частицы вокруг полюса с угловой скоростью