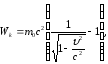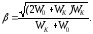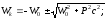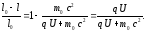Как найти скорость протона физика

Enter the speed of light through the medium into the calculator to determine the proton velocity.

• All Velocity Calculators
• Electron Velocity Calculator
• Sonic Velocity Calculator
• De Broglie Wavelength Equation Calculator
• Material Velocity Calculator
• eV to Velocity Calculator
• Ion Velocity Calculator
• Neutron Velocity Calculator

Proton Velocity Formula

The following equation is used to calculate the Proton Velocity.

PV = C / 100

• Where PV is the proton velocity (m/s)
• C is the speed of light through the medium

What is a Proton Velocity?

Definition:

A proton velocity is typically described as 1% of the speed of light through the medium.

How to Calculate Proton Velocity?

Example Problem:

The following example outlines the steps and information needed to calculate Proton Velocity.

First, determine the speed of light through the medium. In this example, the speed of light through the medium is found to be 299,792,458 m/s.

Finally, calculate the Proton Velocity using the formula above:

PV = C / 100

PV = 299,792,458 / 100

PV = 2,997,924.58 m/s

Движение протона в однородном магнитном поле по окружности происходит под действием силы Лоренца, равной:

F = qvB,

здесь q — заряд протона, v — его скорость, B — индукция магнитного поля.

При этом сила Лоренца является центростремительной:

F = mv^2/r,

здесь m — масса протона, v — его скорость, r — радиус окружности, по которой движется протон.

Таким образом, должно выполняться равенство:

qvB = mv^2/r, откуда

v = qBr/m.

Подставляя в эту формулу числовые значения

q = 1,6*10^(-19) Кл, m = 1,67*10^(-27) кг, В = 5 мТл = 5*10^(-3) Тл, r = 4 см = 0,04 м,

находим:

v = 1,6*10^(-19)*5*10^(-3)*0,04/(1,67*10^(-27)) = 1,6*5*4000/1,67 = 19162 м/с = 19 км/с.

Ответ: 19 км/с.

Решение

Найдём
энергию покоя протона
:

=1,5·10^-10
Дж = 939 МэВ.

Релятивистская
формула кинетической энергии

откуда
находим скорость протона
.
Для простоты преобразований введёмтогдаоткуда

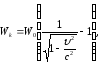
Расчёт
удобнее вести, подставив числовые
значения энергии в МэВ:

.

Ответ:
= 2,988·10⁸
.

Примечание.
После решения задач 5 и 5-А можно сравнить
возможности ускорения протонов и
электронов.

Задача
6. Определить
импульс и кинетическую энергию электрона,
движущегося со скоростью
= 0,9с,
где с
– скорость света в вакууме.

Дано:

=
0,9 с

P
—?
W_k
— ?

Решение

I способ.

Импульс частицы равен произведению
массы частицы на её скорость:

P
= m.
(1)

Так
как скорость электрона близка к скорости
света, то необходимо учесть зависимость
массы от скорости, определяемую по
формуле

,
(2)

где
m
– масса движущейся частицы;
– масса покоящейся частицы;— скорость частицы, выраженная в долях
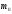
скорости света.

Заменив
в формуле (1) массу m
по формуле (2) и приняв во внимание, что
,
получим

Подставив числовые значения, получим

.

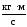
В
релятивистской механике кинетическая
энергия частицы определяется как
разность между полной энергией
и энергией покояэтой частицы, то естьW_k
= m
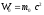
–=(m
–)
.

Учитывая
формулу (2), получим

Подставляя
числовые значения, получим

Дж.

II способ.

Можно
найти кинетическую энергию, используя
формулу связи кинетической энергии W_k
и импульса:

Подставив
числовые значения, получим

Дж.

Ответ:
P
= 5,6·10^-22
,
W_k
= 1,06·10^-13
Дж.

Задача
7. На сколько
процентов изменится продольный размер
протона и электрона после прохождения
ими разности потенциалов U
=
10⁶
В?

Дано:

U
= 10⁶
В

m_p
= 1,67·10 ^-27
кг

m_е
= 9,11·10 ^-31
кг

Решение

Заряд
протона и электрона имеет одинаковые
числовые значения, поэтому они после
прохождения разности потенциалов U
приобретает
одинаковую кинетическую энергию, равную
работе электрического поля:

W_е
= qU
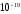
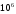
= 1,6··= 1,6·Дж = 1 МэВ.

Продольный размер тела

,

где
– длина в системе, неподвижной относительно
тела;l
– длина
тела, движущегося со скоростью
.

Относительное изменение продольного размера

Из
релятивистской формулы кинетической
энергии найдём значение
:

qU,

откуда

Тогда

Для
электрона

c²
= 0,511 МэВ; для протона

c²
= 939 МэВ.

Подставив
числовые данные, получим для электрона

Для
протона

Ответ:

Задача
8. Ускоритель
сообщил радиоактивному ядру скорость
0,4 с.
В момент вылета из ускорителя ядро
выбросило в направлении своего движения
-частицу
со скоростью 0,75 с
относительно ускорителя. Найти скорость
частицы относительно ядра.

Дано:

=
0,4 с

u
= 0,75 с

—
?

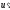
Решение

Скорость
тела u
относительно
неподвижной системы выражается формулой

где
— относительная скорость (скорость тела
относительно движущейся системы
отсчёта);– переносная скорость (скорость
движущейся системы отсчёта).

Преобразуя
это выражение, найдём скорость
:

Подставив
данные, получим

Ответ:

Задача
9. До какой
энергии нужно ускорить частицы в
циклотроне, если относительное увеличение
массы частицы не должно превышать 5 %?
Задачу решить для: а) электронов; б)
протонов.

Дано:

m_e
= 9,1кг

m_p
= 1,67кг

W_k
— ?

Соседние файлы в папке Часть 1

• #
• #
• #
• #
• #
• #
• #
• #

Чему равна скорость протона с кинетической энергией 20 МэВ?

Запишем условие, переведя единицы измерения в единицы СИ.

$1;эВapprox 1,6*10^{-19}$ Дж

Дано:

$E_k=3,2*10^{-12}$ Дж

частица=протон

Найти: v

Кинетическая энергия выражается формулой: 

$E_k=frac{mv^2}{2}$            (1)

где m — масса протона, v — его скорость.

$v=sqrt{frac{2E_k}{m}}$             (2)

Масса протона — известная физическая величина:  

$m=1,67*10^{-27}$ кг

$v=sqrt{frac{2*3,2*10^{-12}}{1,67*10^{-27}}}approx 61905858$ м/с

Ответ: скорость протона приблизительно 61906 км/с

Условие задачи:

Чему равна скорость протона, движущегося в ускорителе, если его масса в 1,25 раз больше его массы покоя?

Задача №11.5.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(m=1,25m_0), (upsilon – ?)

Решение задачи:

Релятивистскую массу (m), т.е. массу протона, движущегося относительно наблюдателя с некоторой скоростью (upsilon), можно определить по формуле:

[m = frac{{{m_0}}}{{sqrt {1 – frac{{{upsilon ^2}}}{{{c^2}}}} }};;;;(1)]

Здесь (m_0) – масса покоя протона, (upsilon) – скорость движения протона относительно наблюдателя, (c) – скорость света в вакууме, равная 3·10⁸ м/с.

По условию задачи динамическая масса протона (m) в 1,25 раз больше его массы покоя (m_0), то есть (m=1,25m_0), поэтому равенство (1) примет вид:

[1,25{m_0} = frac{{{m_0}}}{{sqrt {1 – frac{{{upsilon ^2}}}{{{c^2}}}} }}]

Откуда получим:

[sqrt {1 – frac{{{upsilon ^2}}}{{{c^2}}}} = frac{4}{5}]

Возведем в квадрат обе части полученного равенства:

[1 – frac{{{upsilon ^2}}}{{{c^2}}} = frac{{16}}{{25}}]

Значит:

[frac{{{upsilon ^2}}}{{{c^2}}} = frac{9}{{25}}]

Извлечем квадратный корень из обеих частей:

[frac{upsilon }{c} = frac{3}{5}]

Окончательно имеем:

[upsilon = frac{3}{5}c]

Численный ответ задачи равен:

[upsilon = frac{2}{5} cdot 3 cdot {10^8} = 1,8 cdot {10^8};м/с]

Ответ: 1,8·10⁸ м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

11.5.6 Тело с массой покоя 1 кг движется со скоростью 2*10^8 м/с. Определить массу этого
11.5.8 Во сколько раз масса движущегося электрона v=0,97c больше массы покоя электрона?
11.5.9 Каким импульсом обладает электрон при движении со скоростью, равой 0,8 скорости света