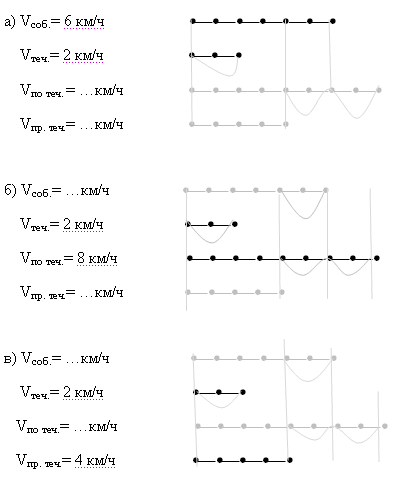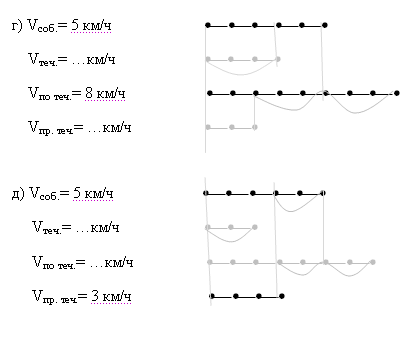Как найти собственную скорость лодки
Решение задач на «движение по воде» многим дается с трудом. В них существует несколько видов скоростей, поэтому решающие начинаю путаться. Чтобы научиться решать задачи такого типа, надо знать определения и формулы. Умение составлять схемы очень облегчает понимание задачи, способствует правильному составлению уравнения. А правильно составленное уравнение — самое главное в решении любого типа задач.

Инструкция
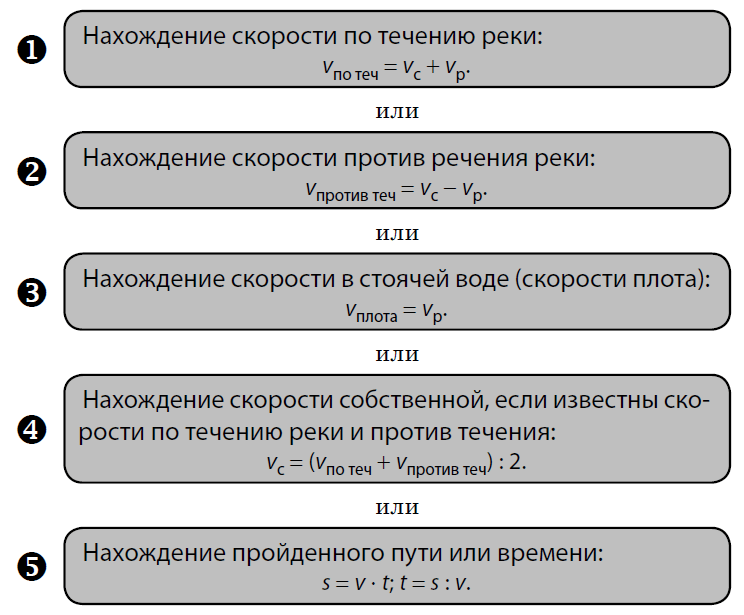
В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
Первое, что необходимо выучить и знать «на зубок» — формулы. Запишите и запомните:
Vпо теч=Vс+Vтеч.
Vпр. теч.=Vс-Vтеч.
Vпр. теч=Vпо теч. — 2Vтеч.
Vпо теч.=Vпр. теч+2Vтеч.
Vтеч.=(Vпо теч. — Vпр. теч)/2
Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.
На примере разберем, как находить собственную скорость и решать задачи такого типа.
Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:
Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)
Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.
За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.
Против теч. По течению
Расстояние 24 24
Скорость Х-3 Х+3
время 24/ (Х-3) 24/ (Х+3)
Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.
20 мин=1/3 часа.
24/ (Х-3) – 24/ (Х+3) = 1/3
24*3(Х+3) – (24*3(Х-3)) – ((Х-3)(Х+3))=0
72Х+216-72Х+216-Х2+9=0
441-Х2=0
Х2=441
Х=21(км/ч) – собственная скорость парохода.
Ответ: 21 км/ч.
Обратите внимание
Скорость плота считается равной скорости водоема.
Источники:
- решение задач на течение
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Рассказываем, как решать задачи на движение по реке. Приводим алгоритм решения и примеры. Задачи для самостоятельного решения.
Суть задач на движение по реке
Задачи на движение по реке – задачи на нахождение скорости, времени и расстояния при движении на реке.
Помни!
В решении задач на движение по реке используются те пункты алгоритма, в которых описано нахождение неизвестной величины (по условию задачи).
Алгоритм решения задач
Алгоритм решения задач на движение по воде:
- Выполняем краткую запись задачи;
- Выбираем способ решения и решаем задачу;
- Выписываем полный ответ.
Выбираем способ решения:
Условные обозначения:
Способы решения задач
Примеры решения задачи
Базовые знания:
Задача 1. Катер прошел 54 км по течению реки и потратил на это 3 ч. Найти скорость течения реки, если собственная скорость катера 16 км/ч.
Краткая запись:
Решение:
1-й способ (арифметический)
- (54:3=18) (км/ч) — скорость по течению;
- (18-16=2) (км/ч) — скорость течения реки.
2-й способ (алгебраический)
- Пусть x км/ч — скорость течения реки, тогда (16 + x) км/ч — скорость катера по течению.
- Так как за 3 часа катер по течению прошел 54 км, составим и решим уравнение:
(3⋅(16+x)=54)
(16+x=54:3)
(16+x=18)
(x=18-16)
(x=2)
Ответ: скорость течения реки равна 2 км/ч.
Задачи для самостоятельного решения
- Расстояние между двумя пристанями 64 км. Скорость течения реки 4 км/ч. Собственная скорость катера равна 12 км/ч. За какое время катер пройдет от одной пристани
до другой по течению реки? - Расстояние между двумя пристанями 64 км. Собственная скорость катера равна 12 км/ч. За какое время катер пройдет расстояние между пристанями против течения реки,
если скорость течения реки 4 км/ч? - Катер курсирует между двумя городами по реке, скорость течения которой равна 6 км/ч. Какое время затратит катет на один рейс туда и обратно, если его собственная скорость 18 км/ч, а расстояние между пристанями — 48 км?
- Моторная лодка преодолевает расстояние 72 км по течению реки за 6 ч, а против течения — за 9 ч. Найти скорость течения реки и собственную скорость лодки.
Посмотреть еще в категории: Задачи по математике 5-6 класс
- Задачи на сложение и вычитание
- Задачи на движение навстречу друг другу
- Задачи на движение в одном направлении
- Задачи на движение в противоположных направлениях
- Задачи на нахождение дроби от числа
- Задачи на нахождение числа по его дроби
- Задачи на нахождение процента от числа
- Задачи на нахождение числа по его процентам
- Задачи на процентное отношение двух чисел
- Задачи на проценты (с помощью пропорции)
- Задачи на нахождение градусной меры угла
- Задачи на нахождение периметра и площади треугольника
- Задачи с использованием формул площадей прямоугольника и квадрата
- Задачи на нахождение объема прямоугольного параллелепипеда и куба
- Задачи на проценты
- Задачи на нахождение длины окружности и площади круга
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 1. Катер движется против течения реки. За сколько часов он преодолеет расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?
Решение: Сначала узнаем скорость движения катера против течения реки, для этого от его собственной скорости отнимем скорость течения:
30 — 2 = 28 (км/ч) — скорость движения катера против течения.
Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:
112 : 28 = 4 (ч).
Решение задачи по действиям можно записать так:
1) 30 — 2 = 28 (км/ч) — скорость движения катера против течения,
2) 112 : 28 = 4 (ч).
Ответ: За 4 часа катер преодолеет расстояние 112 км.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.
Задача 2. Расстояние от пункта A до пункта B по реке равно 120 км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Рассмотрите два варианта:
1) лодка движется по течению реки;
2) лодка движется против течения реки.
Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:
27 + 3 = 30 (км/ч).
Значит расстояние между пунктами лодка преодолеет за:
120 : 30 = 4 (ч).
Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:
27 — 3 = 24 (км/ч).
Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:
120 : 24 = 5 (ч).
Решение задачи по действиям для движения по течению реки можно записать так:
1) 27 + 3 = 30 (км/ч) — скорость лодки,
2) 120 : 30 = 4 (ч).
Для движения против течения реки решение задачи по действиям можно записать так:
1) 27 — 3 = 24 (км/ч) — скорость лодки,
2) 120 : 24 = 5 (ч).
Ответ:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.
Тема: Задачи на движение по реке.
Цели:
- обобщить и систематизировать знания по теме
«Задачи на движение по реке»; - проверить знание теоретического материала,
умение решать задачи арифметическим способом; - развивать кругозор, мышление, внимание,
культуру математической речи; - прививать интерес к математике.
Методы обучения: частично-поисковый
(эвристический), системные обобщения,
самопроверка, взаимопроверка.
Формы организации урока: фронтальная,
индивидуальная.
Оборудование: презентация к уроку,
листы учета знаний.
ХОД УРОКА
I. Организационный момент
Сообщить учащимся цели урока. Настроить ребят
на активную работу.
II. Проверка домашнего задания
№ 391(а).
Собственная скорость теплохода 27км/ч, скорость
течения реки 3 км/ч. Сколько времени затратит
теплоход на путь по течению реки между двумя
причалами, если расстояние между ними 120 км?
Решение:
1) Vпо теч.= Vсоб.+ Vтеч. = 27 + 3 = 30 (км/ч).
2) tпо теч.= S : Vпо теч.= 120 : 30 = 4 (ч.)
Ответ: 4 часа.
№ 392.
Катер, имеющий собственную скорость 15 км/ч,
проплыл 2 часа по течению реки и 3часа против
течения. Какое расстояние проплыл катер за все
время, если скорость течения реки 2 км/ч?
Решение:
1) Vпо теч.= Vсоб. + Vтеч.= 15 + 2 = 17 (км/ч.)
2) Vпр. теч.= Vсоб. – Vтеч.= 15 – 2 = 13 (км/ч.)
3) Sпо теч.= Vпо теч. · tпо теч. = 17 · 2 = 34 (км)
4) Sпр теч.= Vпр. теч.· t пр. теч.=13 · 3 = 39 (км)
5) S=Sпо теч.+ Sпр. теч. = 34 + 39 = 73 (км)
Ответ: 73 км
III. Актуализация знаний
(Фронтальная работа)
Вопросы: (устно или с использованием
проектора.)
1. Что такое собственная скорость катера? Ответ:
скорость катера в стоячей воде (озере, пруду).
2. Что такое скорость течения? Ответ: на какое
расстояние относит река предмет за единицу
времени.
3. Как определяется скорость катера по течению
реки? Ответ: как сумма скорости собственной и
течения.
4. Как определяется скорость катера против
течения? Ответ: как разность скорости
собственной и течения.
5. Как определяется скорость движения плота по
реке? Ответ: как скорость течения реки.
Подведем итог:
Vпо течению – сумма V течения и V
собственной.
V против течения – разность Vсобственной и
Vтечения.
Значит, зная Vпо течению и Vпротив течения, можно
найти Vтечения и Vсобственной.
Вспомним задачу на нахождение двух чисел по их
сумме и разности.
1) (V по теч. – V пр. теч.) : 2 = Vтеч.
2) Vпо теч. – Vтеч. = Vсоб.
IV. Решение задач
№ 1.
Из четырех скоростей (Vсоб.,Vпо теч.,Vпр. теч.,Vтеч.
) две заданы и изображены отрезком. Вычислите две
другие скорости и изобразите их отрезками:
№ 2. Заполним таблицу.
|
Vсоб, км/ч |
V теч, км/ч |
Vпо теч, км/ч |
Vпр. теч, км/ч |
|
15 |
3 |
? |
? |
|
16 |
? |
18 |
? |
|
13 |
? |
? |
10 |
|
? |
2 |
11 |
? |
|
? |
3 |
? |
15 |
|
? |
? |
28 |
24 |
№ 3
Решим задачу № 393 (а).
Расстояние между двумя причалами 24 км. Сколько
времени потратит моторная лодка на путь от
одного причала до другого и обратно, если
собственная скорость моторной лодки 10 км/ч, а
скорость течения 2 км/ч?
Решение:
1) Vпо теч.= Vтеч.+ Vсоб.= 2 + 10 = 12 (км/ч)
2) Vпр. теч. = Vсоб. – Vтеч.= 10 – 2 = 8 (км/ч)
3) tпо теч.= S : Vпо теч.= 24 : 12 = 2 (ч)
4) tпр. теч.= S : Vпр. теч.= 24 : 8 = 3 (ч)
5) t = tпо теч. + tпр. теч.= 2 + 3 = 5 (ч)
Ответ: 5 часов.
V. Самостоятельная работа
|
I вариант |
II вариант |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) Скорость моторной лодки в стоячей воде 15км/ч, а скорость течения реки 3 км/ч. Сколько времени потратит моторная лодка на путь от одной пристани до другой и обратно, если расстояние между пристанями 36 км? 2)
|
1) Скорость моторной лодки в стоячей воде 10 км/ч, а скорость течения реки 2 км/ч. Сколько времени потратит моторная лодка на движение от одной пристани до другой и обратно, если расстояние между пристанями 24 км? 2)
|
VI. Подведение итогов урока
Заполнить карточку самоанализа.
Объявление оценок за урок.
VII. Определение домашнего задания
№ 393 (б), 394 С.М.Никольский, М.К.Потапов,
Н.Н.Решетников, А.В.Шевкин. Математика:
учебник для 6 кл. общеобразовательных
учреждений.– М.: Просвещение, 2008 г.
Презентация
Список литературы:
1. С.М.Никольский, М.К.Потапов, Н.Н.Решетников,
А.В.Шевкин. Математика: учебник для 6 кл.
общеобразовательных учреждений. – М.:
Просвещение, 2008 г.
2. А.В.Шевкин. Обучение решению текстовых
задач в 5-6 классах. – М.: «Русское слово», 2001г.
Описание презентации по отдельным слайдам:
-
1 слайд
Задачи на движение по воде
-
2 слайд
Разминка
1) Вычислить: 3х6:2
2) 97 уменьшить на 60
3) Найти сумму чисел 26 и 70
4) Найти разность чисел 87 и 60
5) Уменьшаемое 74, вычитаемое 20. Найти
разность -
3 слайд
Основные обозначения:
Vсоб. – собственная скорость объекта
Vтеч. – скорость течения реки
V по теч. – скорость объекта по течению
Vпр. теч. – скорость объекта против течения -
4 слайд
Формулы скоростей
V по теч. = Vсоб. + Vтеч.
Vпр. теч = Vсоб. – Vтеч.
Vсоб. = (Vпо теч. + Vпр. теч.) :2
Vтеч. = (Vпо теч. – Vпр. теч.) :2 -
5 слайд
Вопрос №1
Собственная скорость лодки 12 км/ч. Скорость течения реки 4 км/ч. Чему равна скорость лодки по течению реки и против течения реки?
Решение:
1) 12+4=16(км/ч) – скорость лодки по течению реки км/ч;
12-4=8(км/ч) – скорость лодки против течения реки км/ч.
Ответ: 16км/ч; 8км/ч. -
6 слайд
Вопрос №2
Чему равна скорость плота, если скорость реки равна 4 км/ч? Плот плывет по течению реки.
Скорость плота равна скорости реки
Ответ: 4 км/ч. -
7 слайд
Вопрос №3
Скорость реки 5 км/ч. Скорость катера 15 км/ч. Чему равна скорость катера плывущего против течения реки?
V пр теч. = Vсоб. — Vтеч
15 — 5 = 10 (км/ч)
Ответ: 10 км/ч. -
-
9 слайд
Вопрос №4
Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки?
Решение:
23+3=26 (км/ч) – скорость теплохода по течению реки;
26 × 3 = 78 км – путь, который преодолеет теплоход по течению реки.
Ответ: 78 км. -
10 слайд
Вопрос №5
За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение:
15 : 5 = 3 (км/ч) — скорость течения реки;
15 км/ч − 3 км/ч = 12 (км/ч) — скорость теплохода против течения реки;
204 : 12 = 17 (ч) – время движения теплохода.
Ответ: 17ч -
11 слайд
Вопрос №6
Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки, если скорость течения – 4 км/ч.
Решение:
110 : 5 = 22 (км/ч) – скорость, с которой двигалась лодка по реке;
22 + 4 = 26 (км/ч) — собственная скорость лодки.
Ответ: 26 км/ч -
12 слайд
Что узнали сегодня на уроке?
— Как найти собственную скорость, если известна скорость по течению и скорость течения реки.Как найти скорость течения, если известна скорость по течению и собственная скорость.
Как найти собственную скорость, если известна скорость против течения и скорость течения.
Чем отличается движение катера по озеру и реке?
Чем отличается движение плота по озеру и реке?
-
-