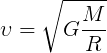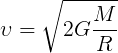Как найти скорость планеты зная радиус

Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса.
Для быстрого расчета можно воспользоваться онлайн-калькулятором.

Первая космическая скорость

Вторая космическая скорость

Пример:

Калькулятор космических скоростей

Orbital velocity is defined as the velocity at which a body circles around another body. The more substantial the body in the centre of attraction is, the higher the orbital velocity for a given height or distance. For an artificial or natural satellite, orbital velocity can be interpreted as the velocity necessary to maintain it in its orbit. Space organizations rely on it heavily to figure out how to launch satellites. It aids scientists in determining the speeds at which satellites must rotate around a planet or celestial body in order to avoid colliding with it.

Formula

The orbital velocity of a satellite orbiting around the Earth is determined by its height above the Earth. More is the orbital velocity, the closer satellite is to the Earth. It is equal to the square root of the product of the gravitational constant and mass of the body divided by the radius of its orbit.

where,

G is the gravitational constant,

M is the mass of object at centre,

R is the radius of the orbit.

Derivation

The formula for orbital velocity is derived through the concepts of gravitational force and centripetal force.

Suppose a satellite of mass m and radius r is orbiting circularly around planet Earth at an altitude h from Earth surface. Let us say, the mass and radius of Earth is M and R respectively. This implies that,

=> r = R + h   ……. (1)

Now, we know that to make the satellite revolve in its orbit, a centripetal force of mV²/r is required. This force is provided by the gravitational force existing between the satellite and the earth.

So, we have

=> mV²/r = GMm/r²

=> V² = GM/r

Using (1), we have

=> V² = GM/(R + h)

As (R + h) ≈ R, we get

This derives the formula for orbital velocity of an object or satellite revolving around a planet.

Sample Problems

Problem 1. Find the orbital velocity of an object revolving around the planet Earth if the radius of Earth is 6.5 × 10⁶ m, the mass of Earth is 5.9722 × 10²⁴ kg and the gravitational constant G is 6.67408 × 10^-11 m³ kg^-1 s^-2.

Solution:

We have,

G = 6.67408 × 10^-11

R = 6.5 × 10⁶

M = 5.9722 × 10²⁴

Using the formula we have,

V = √(GM/R)

= (6.67408 × 10^-11)(5.9722 × 10²⁴)/(6.5 × 10⁶)

= 29.8 km/s

Problem 2. Find the orbital velocity of an object revolving around the planet Mercury if the radius of Mercury is 2439.7 km, the mass of Mercury is 0.33 × 10²⁴ kg and the gravitational constant G is 6.67408 × 10^-11 m³ kg^-1 s^-2.

Solution:

We have,

G = 6.67408 × 10^-11

R = 2439.7

M = 0.33 × 10²⁴

Using the formula we have,

V = √(GM/R)

= (6.67408 × 10^-11)(0.33 × 10²⁴)/(2439.7)

= 47.4 km/s

Problem 3. Find the orbital velocity of an object revolving around the planet Venus if the radius of Venus is 6051.8 km, the mass of Venus is 4.87 × 10²⁴ kg and the gravitational constant G is 6.67408 × 10^-11 m³ kg^-1 s^-2.

Solution:

We have,

G = 6.67408 × 10^-11

R = 6051.8

M = 4.87 × 10²⁴

Using the formula we have,

V = √(GM/R)

= (6.67408 × 10^-11)(4.87 × 10²⁴)/(6051.8)

= 35 km/s

Problem 4. Find the orbital velocity of an object revolving around the planet Mars if the radius of Mars is 3389 km, the mass of Mars is 0.642 × 10²⁴ kg and the gravitational constant G is 6.67408 × 10^-11 m³ kg^-1 s^-2.

Solution:

We have,

G = 6.67408 × 10^-11

R = 3389

M = 0.642 × 10²⁴

Using the formula we have,

V = √(GM/R)

= (6.67408 × 10^-11)(0.642 × 10²⁴)/(3389)

= 24.1 km/s

Problem 5. Find the orbital velocity of an object revolving around the planet Jupiter if the radius of Jupiter is 69911 km, the mass of Jupiter is 1898 × 10²⁴ kg and the gravitational constant G is 6.67408 × 10-11 m3 kg-1 s-2.

Solution:

We have,

G = 6.67408 × 10^-11

R = 69911

M = 1898 × 10²⁴

Using the formula we have,

V = √(GM/R)

= (6.67408 × 10^-11)(1898 × 10²⁴)/(69911)

= 13.1 km/s

Problem 6. Find the orbital velocity of an object revolving around the planet Saturn if the radius of Saturn is 58232 km, the mass of Saturn is 568 × 10²⁴ kg and the gravitational constant G is 6.67408 × 10-11 m3 kg-1 s-2.

Solution:

We have,

G = 6.67408 × 10^-11

R = 58232

M = 568 × 10²⁴

Using the formula we have,

V = √(GM/R)

= (6.67408 × 10^-11)(568 × 10²⁴)/(58232)

= 9.7 km/s

Problem 7. Find the orbital velocity of an object revolving around the planet Uranus if the radius of Uranus is 25362 km, the mass of Uranus is 86.8 × 10²⁴ kg and the gravitational constant G is 6.67408 × 10-11 m3 kg-1 s-2.

Solution:

We have,

G = 6.67408 × 10^-11

R = 25362

M = 86.8 × 10²⁴

Using the formula we have,

V = √(GM/R)

= (6.67408 × 10^-11)(86.8 × 10²⁴)/(25362)

= 6.8 km/s

Last Updated :
27 Apr, 2022

Like Article

Save Article

С древних времен людей интересовала проблема устройства мира. Еще в III-м веке до нашей эры греческий философ Аристарх Самосский высказал идею о том, что Земля вращается вокруг Солнца, и попытался вычислить расстояния и размеры Солнца и Земли по положению Луны. Так как доказательный аппарат Аристарха Самосского был несовершенен, большинство осталось сторонниками пифагорейской геоцентрической системы мира.
Прошло почти два тысячелетия, и идеей гелиоцентрического устройства мира увлекся польский астроном Николай Коперник. Он умер в 1543 году, и вскоре труд всей его жизни опубликовали ученики. Модель и таблицы положения небесных тел Коперника, основанные на гелиоцентрической системе, гораздо точнее отражали положение вещей.
Спустя полвека немецкий математик Иоганн Кеплер, используя скурупулезные записи датского астронома Тихо Браге о наблюдениях небесных тел, вывел законы движения планет, которые сняли неточности модели Коперника.
Завершение XVII века ознаменовалось трудами великого английского ученого Исаака Ньютона. Законы механики и всемирного тяготения Ньютона расширили и дали теоретическое обоснование формулам, выведенным из наблюдений Кеплером.
Наконец, в 1921 году Альберт Эйнштейн предложил общую теорию относительности, наиболее точно описывающую механику небесных тел в настоящее время. Ньютоновские формулы классической механики и теории гравитации до сих пор могут применяться для некоторых вычислений, не требующих большой точности, и там, где релятивистскими эффектами можно пренебречь.

Благодаря Ньютону и его предшественникам мы можем вычислить:

• какую скорость должно иметь тело для сохранения заданной орбиты (первая космическая скорость)
• с какой скоростью должно двигаться тело, чтобы оно преодолело притяжение планеты и стало спутником звезды (вторая космическая скорость)
• минимальную необходимую скорость выхода за пределы планетной системы (третья космическая скорость)

Первая космическая скорость тела —

это скорость, которую следует придать телу для сохранения телом заданной круговой орбиты. Первая космическая скорость определяется по формуле: ,где
R=r+h — радиус орбиты, складывающийся из r — радиуса планеты и h — высоты над планетой
M — масса планеты
G — гравитационная постоянная, равная 6.67408(31)10^-11 м³/(с²·кг)
Формула легко выводится из формул силы притяжения и центробежной силы, равенство которых тело испытывает, вращаясь на заданной орбите R вокруг тела превосходящей массы M

m — масса тела (исключается при выводе v₁)

Больше чем через 250 лет после открытий Ньютона Советский Союз запустил в 1957 году первый искусственный спутник Земли. Ракета носитель Р-7 вывела Спутник-1 на орбиту высотой 577 километров.

Вторая космическая скорость,

или скорость освобождения тела, это минимальная скорость, которую следует придать телу для того, чтобы оно вышло за пределы влияния планеты.
Скорость освобождения определяется по формуле:
Соотносится с первой космической скоростью следующим образом:
Формула выводится исходя из соображения, что кинетическая энергия должна быть равна работе по преодолению силы тяжести в диапазоне расстояний от поверхности планеты до бесконечности:

В 1959 году Советский Союз запустил автоматическую межпланетную станцию Луна-1, которая стала искусственным спутником Солнца — так была достигнута вторая космическая скорость.

Третья космическая скорость

Минимальная скорость, которую необходимо придать находящемуся вблизи поверхности планеты телу, чтобы оно могло покинуть пределы планетарной системы.
,
где v — орбитальная скорость планеты
v₂ — вторая космическая скорость планеты

Согласно расчетам, аппарат, запущенный с Земли, должен обладать скоростью 16.6 км/с, чтобы покинуть пределы Солнечной системы.
Близкую к третьей космической (16.26 км/с) развил при старте в 2006 году аппарат «Новые Горизонты», запущенный в США для исследования Плутона и его спутника Харона. Сейчас аппарат завершил съемку Плутона и направляется к поясу Койпера.
Первым в истории искусственным аппаратом, достигшим третьей космической скорости стал «Вояджер-1». Его запустили Соединенные Штаты в 1977 году. Начальная скорость Вояджера-1 была ниже, чем у «Новых горизонтов», но благодаря серии гравитационных маневров около планет солнечной системы аппарат достиг скорости 17 км/с. В августе 2012-го аппарат вышел за границы Солнечной системы, на данный момент собираемые им данные продолжают поступать.
Аппарат несет 12-дюймовый позолоченный диск с посланием к внеземным цивилизациям.

Источники:
В.Захаров Тяготение: от Аристотеля до Эйнштейна
Фото NASA, проект Вояджер.

Условие задачи:

Определить первую космическую скорость для планеты, масса и радиус которой в два раза больше, чем у Земли.

Задача №2.5.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(R=2R_3), (M=2M_з), (upsilon_1-?)

Решение задачи:

Первая космическая скорость – это скорость, которую нужно сообщить телу, чтобы оно стало спутником некоторой планеты. Её можно найти из следующих соображений. При движении спутника по круговой орбите сила тяготения сообщает ему центростремительное ускорение, поэтому второй закон Ньютона даст такое равенство:

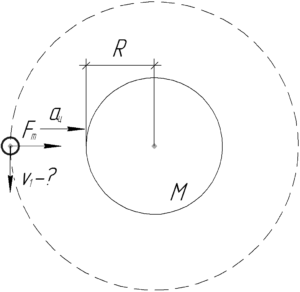
[{F_т} = m{a_ц};;;;(1)]

Силу тяготения найдем из закона всемирного тяготения, учитывая, что высота орбита мала, т.е. она является околоземной:

[{F_т} = Gfrac{{Mm}}{{{R^2}}};;;;(2)]

Центростремительное ускорение спутника, движущегося со скоростью (upsilon_1), равно:

[{a_ц} = frac{{upsilon _1^2}}{R};;;;(3)]

В равенство (1) подставим выражения (2) и (3):

[Gfrac{{Mm}}{{{R^2}}} = frac{{mupsilon _1^2}}{R}]

Значит первую космическую скорость можно определять по такой формуле:

[{upsilon _1} = sqrt {Gfrac{M}{R}} ]

По условию (R=2R_3) и (M=2M_з), поэтому:

[{upsilon _1} = sqrt {Gfrac{{2{M_з}}}{{2{R_з}}}}  = sqrt {Gfrac{{{M_з}}}{{{R_з}}}} ]

В принципе после получения этой формулы можно было сказать, что первая космическая скорость на данной планете такая же, как и у Земли. Но мы “добьём” задачу до конца.

Домножим и поделим дробь под корнем на (R_3), тогда:

[{upsilon _1} = sqrt {Gfrac{{{M_з}}}{{R_з^2}} cdot {R_з}} ]

Выражение ({Gfrac{{{M_з}}}{{R_з^2}}}) равно ускорению свободного падения (g) вблизи поверхности Земли, в итоге имеем:

[{upsilon _1} = sqrt {g{R_з}} ]

Напомним, что радиус Земли равен 6,4·10⁶ м, поэтому численный ответ равен:

[{upsilon _1} = sqrt {10 cdot 6,4 cdot {{10}^6}}  = 8000; м/с]

Ответ: 8000 м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.5.6 На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения
2.5.8 На некоторой планете сила тяжести, действующая на тело массой 4 кг, равна 8 Н. Найти
2.5.9 На сферической планете вес тела на полюсе в 3 раза больше веса тела на экваторе