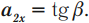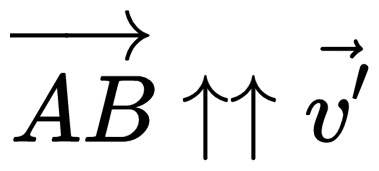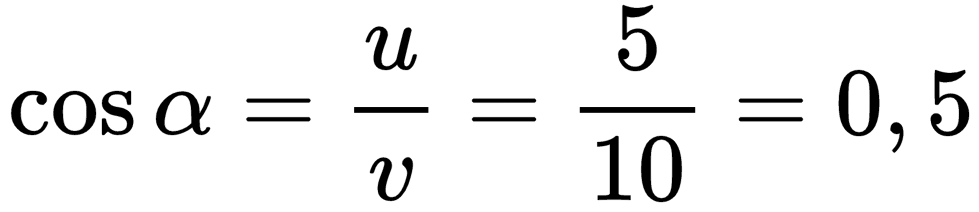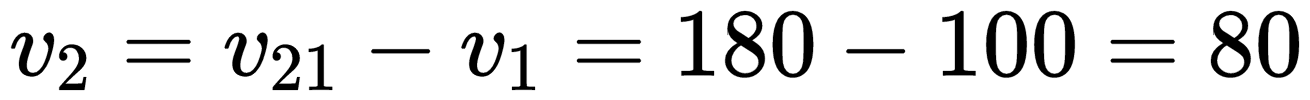Как найти скорость одного тела относительно другого

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно! 
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

3. по скорости

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

4. по ускорению

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( S )​ — перемещение тела относительно неподвижной системы отсчета;
​( S_1 )​ — перемещение тела относительно подвижной системы отсчета;
​( S_2 )​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​( v )​ — скорость тела относительно неподвижной системы отсчета;
​( v_1 )​ — скорость тела относительно подвижной системы отсчета;
​( v_2 )​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):

Определим скорость второго тела относительно первого ( v_{21} ):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​( alpha )​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​( v )​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​( a )​, единица измерения — м/с².
В векторном виде:

где ​( v )​ – конечная скорость; ​( v_0 )​ – начальная скорость;
​( t )​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​( a_n )​ – нормальное ускорение, ​( a_{tau} )​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ​( v )​ ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​( t )​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​( t )​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.

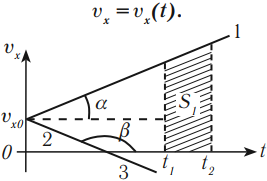
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​( x=x(t) )​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​( a_x )​ > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ​( v_{0x} )​ > 0, ​( a_x )​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,

График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ​( t_2-t_1 )​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​( n )​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​( g )​, единицы измерения – м/с².

Важно! ( g ) = 9,8 м/с², но при решении задач считается, что ( g ) = 10 м/с².

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​( v_0 )​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​( v )​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​( v_0=v_{0x} )​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​( g )​ и без начальной скорости ​( v_{0y}=0 )​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​( v_0 )​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​( alpha )​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​( a_{цс} )​, единицы измерения – ​м/с^2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​( T )​, единицы измерения – с.

где ​( N )​ – количество оборотов, ​( t )​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​( nu )​, единицы измерения – с^–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​( v )​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​( omega )​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​( v_1 )​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​( (m) )​ равна нулю, мгновенная скорость в верхней точке ​( (n) )​ равна удвоенной скорости ​( v_1 )​, мгновенная скорость точки ​( (p) )​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​( (c) )​ – по теореме косинусов.

Основные формулы по теме «Кинематика»

Let us suppose we are travelling on a Bus, let’s say, another bus overtakes us. We will not feel the actual speed of the overtaking bus, as felt by a person who looks it, standing by the side of the road. If both the buses are moving at the same speed in the same direction, a person in one bus observes a person in the other bus at rest, even though both are in motion. If both buses are in the opposite direction, then the passengers observe a greater speed, greater than their individual speed. In all these situations, we measure the relative velocities. Thus, 

The relative is the velocity of one body with respect to another body. It is measured as the rate of change of position of a body with respect to another body.

In Mathematics, the relative velocity is the vector difference of the velocities between the two bodies.

What is Relative Velocity? 

The velocity of a body with respect to the velocity of another body is called the relative velocity of the first body with respect to the second.

Relative velocity = Velocity of the first body – Velocity of the second body

If Va and Vb represent the velocities of two bodies A and B respectively at any instant, then, the relative velocity of A with respect to B is represented by V_ab.

Then, V_ab  = V_a – V_b                                                                                                                                                                                               ……(1)

Similarly, the relative velocity of B with respect to A is given by,

V_ba  = V_b – V_a                                                                                                                                                                                                         ……(2)

So, from the equations (1) and (2), we can write      

V_ba  =  – V_ab

This implies that 

Relative velocity of A with respect to B = – Relative velocity of B with respect to A

Henceforth, the magnitude of both relative velocities are equal to each other.

• Difference between velocity and relative velocity: The difference between velocity and relative velocity is that velocity is measured with respect to a reference point which is relative to a different point. While relative velocity is measured in a frame where an object is either at rest or moving with respect to the absolute frame.
• Dimension Unit of relative velocity: The dimension Unit of relative velocity is similar to the unit of velocity may be expressed as – [ M⁰L¹T^-1].

Case 1: Relative Velocity for two objects moving in the same direction with equal velocities.

Let’s now consider four different cases regarding relative motion. In the first case let us suppose two cars A and B are moving in the same direction with equal velocities (Va = Vb). For a person seated in A, the car B would appear to be at rest, if he forgets for a moment the fact that he himself is in motion. Hence the velocity of B relative to A is zero. 

V_ba= V_b– V_a= 0 (as V_a=V_b)

Similarly, in the case of a person seated in car B and observing car A. The relative velocity of A with respect to B is also zero.  

V_ab = V_a– V_b = 0  (as V_a=V_b)

So, if V_b – V_a  = 0, means the two cars are moving in the same direction and are keeping the same distance between them always. So their position-time graphs are two parallel straight lines.

Case 2: Relative velocity for two objects starting from the same point and moving in the same direction with unequal velocities.

In this case let Car A is moving with a velocity Va and Car B,(starting from the same point or X₁(0)=X₂(0) ), be moving with a greater velocity V_b in the same direction. Then, the person in car A feels that bus B is moving away from him with velocity, 

V_ba = V_b – V_a

And for an observer in car B, car A appears to go back with a velocity, 

V_ab = V_a-V_b = – (V_b– V_a )

Velocity of A with respect to B= – (Velocity of B with respect to A)

That is, the velocity of A relative to B is the negative of the velocity of B relative to A.

Case 3: Relative velocity for two objects starting from different positions and moving in the same direction with unequal velocities

Here, V_a> V_b. If car A which is having the higher velocity and moving behind the car B, then car A will overtake the car B at some instant and the position-time graphs of the two cars will intersect at a point 

V_ab=V_a-V_b ≠0 and 

V_ba=V_b-V_a ≠0 as V_a > V_b

And V_b > V_a. If the car with greater velocity(in this case car B) is moving ahead, there is no chance of overtaking the other car A and hence the position-time graphs will not intersect, both the lines move far from each other as shown in the graph

V_ab=V_a-V_b ≠0 and

V_ba=V_b-V_a ≠0 as  V_b> V_a

Clearly, If V_b – V_a ≠ 0, means the two cars are moving with unequal velocities. Their position-time graphs are straight lines inclined to the time axis and one of them will be steeper than the other.

Case 4: Relative velocity for two objects moving in the opposite direction

If both the cars are moving in opposite directions as shown in the figure, the relative velocity of V_ba or V_ab will be

V_ba=V_b-(-V_a) = V_b+V_a, 

Similarly, 

V_ab=V_a-(-V_b) = V_a+V_b  

or 

V_ab=V_ba=V_a+V_b

It means, when two cars A and B are moving in opposite directions each seems to go very fast relative to the other.  

Sample Problems

Problem 1: Bus A travel with a speed of 40 m/s towards North and bus B travel with a speed of 60 m/s towards South. What is the relative velocity?

Solution:

Speed of bus A= V_a = 40 m/s (towards north)

Speed of bus B= V_b = 60 m/s (towards south)

As both the buses are moving in opposite direction, so relative velocity is: 

Vab = Va – (-Vb) 

       = 40 – (-60) 

       = 100 m/s

Problem 2: Two trucks, standing a few distances apart, start moving towards each other with speeds 1 m/s and 2 m/s along a straight road. What is the speed with which they approach each other?

Solution: 

Let us consider that “A” denotes any truck at rest, “B” denotes first truck and “C” denotes second truck. The equation of relative velocity for this case is :

⇒ V_ca = V_ba + V_bc

V_ba = V_b-V_a =1-0=1m/s , 

V_ca= V_ba + V_bc=-2-0=-2m/s

V_ba = 1 m/s and V_ca= − 2 m/s 

Using,

V_ca  = V_ba + V_cb

− 2 = 1 + V_cb

V_cb = − 2 − 1 

     = − 3 m/s 

It means that the truck “C” is approaching “B” with a speed of -3 m/s along the straight road. Or, it means that the truck “B” is approaching “C” with a speed of 3 m/s along the straight road. We, therefore, say that the two trucks move towards each other each with a relative speed of 3 m/s.

Problem 3: Two cars, initially 900 m distant apart, start moving towards each other with speeds 1 m/s and 2 m/s along a straight road. When would they meet?

Solution:

The relative velocity of two cars (say 1 and 2) is:  V₂₁ = V₂-V₁

Let us consider that the direction V₁ is moving in a positive direction.

Here, V₁ = 1 m/s and V₂ = -2 m/s. So, relative velocity of two cars (of 2 w.r.t 1) is : ⇒ V₂₁ = − 2 − 1 = − 3 m / s

This means that car “2” is approaching car “1” with a speed of -3 m/s along the straight road.

Similarly, car “1” is approaching car “2” with a speed of 3 m/s along the straight road. Therefore,

So can say that two cars are approaching at a speed of 3 m/s. Now, let the two cars meet after time:   

t = Displacement ⁄ Relative velocity 

  = 900/3 = 30 sec. 

Problem 4: How long will a girl sitting near the window of a train travelling at 36 km h-1 see a train passing by in the opposite direction with a speed of 18 km/h? The length of the slow-moving train is 90 m.

Solution: 

Given : Velocity of train = V_t = 36 Km/h = 36 × 5/18 m/s = 10 m/s

Velocity of passenger moving in opposite direction = Vp = 18 Km/h = 18 × 5/18 m/s = 5 m/s

The relative velocity of the slow-moving train with respect to the girl is V_tp =  V_t – (-V_p) = V_t + V_p

V_tp =  (10 + 5) m/s = 15 m/s.

As the girl will watch the full length of the other train, to find the time taken to watch the full train:

Using relative speed = distance / time

                             15 = 90/t

                               t = 90/15 

                                 = 6 sec 

Problem 5: A girl, moving at 3 km/hr along a straight line, finds that the raindrops are falling at 4 km/hr in the vertical direction. Find the angle with which raindrop hits the ground.

Solution:

Let the girl be moving in the x-direction. Let us also denote girl with “A” and raindrop with “B”. we need to know the direction of raindrop with respect to ground=V_b.

Here Given

V_a=3km/hr  , V_b =?  ,  V_ba =4km/hr  

Using equation, V_ba = V_b-V_a

 So V=V_a+V_ba

In ΔOQR, Angle with which rain drop hits the ground = ∠QOR = θ 

So tanθ= V_a/V_ba

tanθ=3/4   

Hence,

θ= tan^-1(3/4) 

or

θ = 37° 

Problem 6: A bus starting from a point travels towards the east with a velocity of 3 m/s. Another bus starting from the point travels towards the north with a  velocity. of 4 m/s. Find the magnitude of the relative velocity of one with respect to another.

Solution:

Given that, 

The Bus-A moves towards East with velocity = V_a = 3 m/s

And Bus-B moves towards North with velocity = V_b =4 m/s

Now the relative velocity V_ba of Bus-B with respect to Bus-A is towards the west of north direction as shown in the figure

Magnitude of V_ba = √3²+4²  => V_ba = 5 m/s 

Similarly, relative velocity Vab of Bus-A with respect to Bus-B is towards the south of east direction as shown in the figure, so:

Magnitude of V_ab = √4²+3²  

Hence, 

V_ab = 5 m/s

§ 9.3. Скорость относительного движения двух тел. Развитие темы

Пусть два тела движутся вдоль одной прямой и мы знаем скорости этих тел. Как найти, с какой скоростью движется одно из этих тел относительно другого? Рассмотрим сначала случай, когда скорости тел направлены одинаково.

Решим задачу

Из поселка одновременно выехали в одном направлении грузовик со скоростью 40 км/ч и легковой автомобиль со скоростью 60 км/ч. С какой скоростью движется легковой автомобиль относительно грузовика?

Решение. За час грузовик проедет 40 км, а легковой автомобиль проедет 60 км. Расстояние между ними будет равно разности расстояний, пройденных автомобилями, то есть 20 км (рис. 9.2). Значит, легковой автомобиль движется относительно грузовика со скоростью 20 км/ч.

Рис 9.2. Начальное положение автомобилей обозначено черным кружком, положение грузовика через час после начала движения — зеленым, а легкового автомобиля — синим

Рассмотрим теперь случай, когда скорости тел направлены противоположно.

Решим задачу

Из поселка одновременно выехали в противоположных направлениях грузовик со скоростью 40 км/ч и легковой автомобиль со скоростью 60 км/ч. С какой скоростью движется легковой автомобиль относительно грузовика?

Решение. За час грузовик проедет 40 км, а легковой автомобиль проедет 60 км. Но расстояние между ними будет равно теперь сумме расстояний, пройденных автомобилями (рис. 9.3), то есть 100 км. Значит, легковой автомобиль движется относительно грузовика со скоростью 100 км/ч.

Рис. 9.3. Начальное положение автомобилей (черный кружок) и их положение через час после начала движения (зеленый и синий кружки)

Итак, если два тела движутся в противоположных направлениях со скоростями v₁ и v₂, то одно тело движется относительно другого со скоростью v_отн = v₁ + v₂ При этом расстояние между телами может как увеличиваться, так и уменьшаться: например, если автомобили едут навстречу друг другу. Рассмотрим это на следующем примере.

Решим задачу

Из двух городов, расстояние между которыми 300 км, одновременно навстречу друг другу по прямой дороге выехали грузовик и легковой автомобиль. Скорость грузовика 40 км/ч, а легкового автомобиля — 60 км/ч. Через какое время после выезда автомобилей расстояние между ними будет равно 100 км?

Решение. Так как автомобили едут в противоположных направлениях, то один автомобиль движется относительно другого со скоростью v_отн = v₁ + v₂ = 40 км/ч + 60 км/ч = 100 км/ч. До встречи автомобили сближаются, то есть расстояние между ними уменьшается. Поскольку в начальный момент расстояние между ними было равно 300 км и каждый час оно уменьшается на 100 км, то расстояние между автомобилями станет равным 100 км через 2 ч после выезда. Но это не единственный ответ! Ведь после встречи, которая произойдет через 3 ч после выезда автомобилей, они начнут удаляться друг от друга, и расстояние между ними будет теперь увеличиваться на 100 км каждый час. Значит, есть еще один момент времени, когда расстояние между автомобилями будет равно 100 км: он наступит через час после встречи автомобилей, то есть через 4 ч после их выезда. Решить задачу — значит найти все ответы!

Источник

Относительность механического движения

теория по физике 🧲 кинематика

Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.

Относительность перемещения

Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.

Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.

Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:

Относительность скорости в ПСО и НСО

Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.

Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.

Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.

Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:

Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):

Косинусу 0,5 соответствует угол, равный 60 градусам.

Относительная скорость двух тел

Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.

Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:

v _отн — относительная скорость, или скорость первого тела относительно второго, v ₁ и v ₂ — скорость первого и второго тела относительно СО.

Варианты обозначения относительной скорости и их проекций:

Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.

Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.

Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:

Скорость второго автомобиля относительно дороги равна 80 км/час.

Правила сложения векторов

Сложение двух сонаправленных векторов
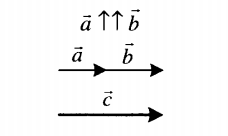	Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону. Его длина равна сумме длин слагаемых векторов: c = a + b.
Сложение двух противоположно направленных векторов
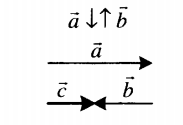	Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|.
Сложение двух векторов, расположенных друг к другу под углом
Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов.
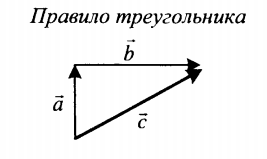	Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: .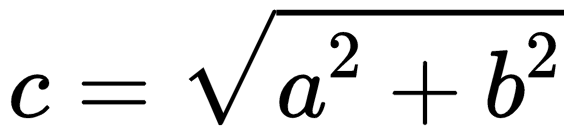
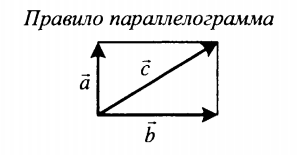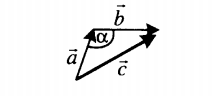	Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .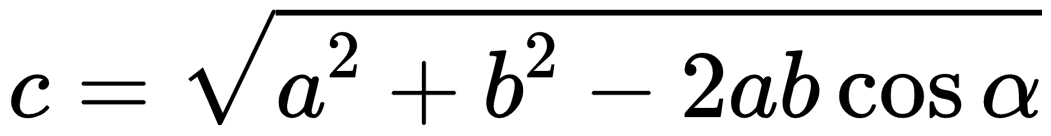
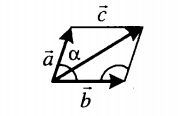	Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: .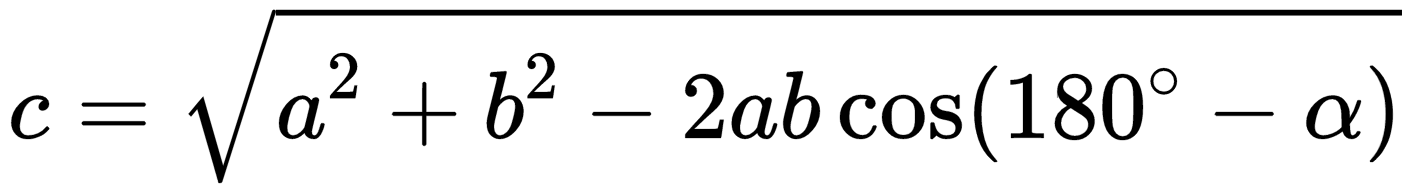

Правила вычитания векторов

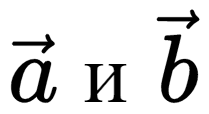
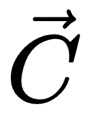
Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор .

Алгоритм решения

Решение

Записываем данные относительно Земли:

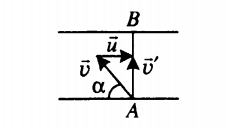
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость второго автомобиля относительно оси ОХ ( v ₂), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ ( v ₁).

Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Записываем закон сложения скоростей в векторном виде:

v ′ — скорость автомобиля относительно земли ( v ₁), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли ( v ₂). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:

Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:

По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Скорость относительного движения двух тел (окончание)

Р е ш е н и е. За час грузовик проедет 40 км, а легковой автомобиль проедет 60 км. Но расстояние между ними будет равно теперь сумме расстояний, пройденных автомобилями (рис. 9.3), то есть 100 км. Значит, легковой автомобиль движется относительно грузовика со скоростью 100 км/ч.

Рис. 9.3. Начальное положение автомобилей (чёрный кружок) и их положение через час после начала движения (зелёный и синий кружки)

Итак, если два тела движутся в противоположных направления со скоростями υ₁ и υ₂, то одно тело движется относительно другого со скоростью υ_отн = υ₁ + υ₂. При этом расстояние между телами может как увеличиваться, так и уменьшаться: например, если автомобили едут навстречу друг другу. Рассмотрим это на следующем примере.

Из двух городов, расстояние между которыми 300 км, одновременно навстречу друг другу по прямой дороге выехали грузовик и легковой автомобиль. Скорость грузовика 40 км/ч, а легкового автомобиля — 60 км/ч. Через какое время после выезда автомобилей расстояние между ними будет равно 100 км?

Р е ш е н и е. Так как автомобили едут в противоположных направлениях, то один автомобиль движется относительно другого со скоростью υ_отн = υ₁ + υ₂ = 40 км/ч + 60 км/ч = 100 км/ч. До встречи автомобили сближаются, то есть расстояние между ними уменьшается. Поскольку в начальный момент расстояние между ними было равно 300 км и каждый час оно уменьшается на 100 км, то расстояние между автомобилями станет равным 100 км через 2 ч после выезда. Но это не единственный ответ! Ведь после встречи, которая произойдёт через 3 ч после выезда автомобилей, они начнут удаляться друг от друга, и расстояние между ними будет теперь увеличиваться на 100 км каждый час. Значит, есть ещё один момент времени, когда расстояние между автомобилями будет равно 100 км: он наступит через час после встречи автомобилей, то есть через 4 ч после их выезда. Решить задачу — значит найти все ответы!

Источник

Эксперты ГКСЭ раскрыли секрет, как они определяют скорость в момент ДТП

Некуда спешить

«Почти всегда после аварии встает вопрос о скоростном режиме»

По некоторым подсчетам, ежегодно в результате ДТП во всем мире гибнут 1,3 миллиона человек. То есть один человек каждые 24 секунды. Казалось бы, пандемия должна была положительно повлиять на дорожную статистику, ведь многие перешли на удаленную работу и учебу. По данным ВОЗ, с начала 2020 года загруженность на дорогах действительно снизилась. Это привело к уменьшению числа аварий. Однако количество летальных исходов в пропорциональном отношении не уменьшилось. По пустым дорогам люди стали ездить быстрее.

— Почти всегда после аварии встает вопрос о скоростном режиме. Насколько быстро ехали водители и могли ли они предотвратить ДТП? Классическая ситуация: автомобиль при повороте налево сталкивается с движущимся с превышением скорости прямо мотоциклом, — рассказывает начальник отдела автотехнических экспертиз центрального аппарата ГКСЭ подполковник юстиции Алексей Жуган. — В правилах черным по белому прописано, что при повороте налево водитель обязан уступить дорогу транспортным средствам во встречном направлении. Есть много «но». Как далеко должен смотреть водитель поворачивающего налево автомобиля, должен ли он предполагать, что между стоящими транспортными средствами станет проезжать мотоцикл, мог ли заметить движущийся на большой скорости мотоцикл? Наша задача — дать экспертную оценку действиям каждого участника происшествия.

Алексей Жуган — о том, как определяют скорость:

— Основной источник — следовая информация на месте ДТП. Однако ее может и не быть. Тогда используются видеозаписи как со стационарных камер видеонаблюдения, так и с видеорегистраторов в салоне. Чем больше относящейся к происшествию информации зафиксировано, тем точнее получится установить скоростной режим. При этом можно учесть и степень повреждения каждого из участников.

Основная масса автотехнических экспертиз назначается по легковым машинам.

Мало кто из водителей знает, что в арсенале судебных экспертов есть специальный программный комплекс, который помогает определить скорость по электронным блокам управления авто. В них аккумулируется такая важная для понимания всех обстоятельств аварии информация, как количество человек в салоне, их расположение, скорость.

— Как правило, в электронных блоках фиксируется скоростной режим движения за пять секунд до столкновения и две секунды после него, содержится информация о положении педалей газа и тормоза. Случается, водитель утверждает, что тормозил, а мы видим, что было по-другому.

Для ДТП пять секунд — это очень большое время, его хватает, чтобы аварию предотвратить. При расчете остановочного пути в экспертной практике применяется минимальное время реакции водителя — 0,6 секунды.

— Из недавних неординарных дел есть еще один пример. В ноябре прошлого года Toyota на высокой скорости выехала на площадь Победы в центре Минска, налетев на ступени монумента, загорелась и перевернулась, — подключается к разговору государственный судебный эксперт отдела автотехнических экспертиз центрального аппарата ГКСЭ Константин Савицкий, приводя резонансный пример. — Машина сильно выгорела, но блоки управления уцелели. Из них мы смогли извлечь все интересующие правоохранителей сведения. Оказалось, что скорость превышала разрешенную на данном участке почти в два раза и была более 130 км/ч. Причем водитель даже не пытался тормозить. Скоростной режим автомобиля мы получили, прочитав информацию в блоках управления. И подтвердили данные, исследовав предоставленные видеозаписи с места происшествия.

Кстати, по данным ГАИ, водителя Toyota штрафовали более 40 раз и даже лишали права управления за вождение в пьяном виде.

В арсенале судебных экспертов есть специальный программный комплекс, который помогает определить скорость по электронным блокам управления авто.

Да вы гоните!

Те самые электронные блоки есть почти во всех современных автомобилях.

— Допустим, водитель попал в ДТП, будучи пьяным или не имея права управления. Инспекторам ГАИ говорит, что за рулем был не он… — моделирую ситуацию.

— С помощью нашего прибора мы можем определить, сколько именно человек находилось в салоне и на каких местах они сидели. Поэтому если водитель ехал один, то такая уловка точно не пройдет, — объяснил Константин Савицкий.

Рассмотрим другую ситуацию, которую мы наблюдаем чаще. В салоне было несколько человек, некоторые погибли. Пытаясь уйти от ответственности, выживший водитель говорит, что за рулем сидел кто-то из погибших. В таких случаях назначается комплексная судебная экспертиза с привлечением судебных экспертов-автотехников и судебно-медицинских экспертов, чтобы определить, кто именно управлял автомобилем.

…В основном автотехнические экспертизы проводятся по легковым машинам. Хотя бывают и по грузовикам, маршруткам, троллейбусам. В летний сезон к этому списку добавляются мотоциклы.

Техника ГКСЭ позволяет при установлении обстоятельств аварии определить, сколько именно человек находилось в салоне и на каких местах они сидели.

Опираясь на личный опыт работы на местах аварий, Алексей Жуган объясняет, что риск летального исхода в случае столкновения автомобиля может быть и при скорости 60 км/ч. Бывали случаи сильного травмирования и даже гибели при резком торможении на сравнительно небольших скоростях. Например, при перевозке груза. Резкое нажатие на тормоз — и груз по инерции перемещается вперед и травмирует людей в салоне…

Разговор заходит о ночных заездах столь нелюбимых минчанами стритрейсеров. Нередко такие погони за адреналином заканчиваются авариями. Недавно эксперты ГКСЭ проводили автотехническую экспертизу по одному «интересному ДТП». У страховой компании возникли к владельцу вопросы. Оказалось, любитель гонять по городу с характерным отстрелом для более эффективного разгона отключил часть систем безопасности. Это стало причиной потери курсовой устойчивости и, как следствие, привело к аварии. Эксперты также установили, что перед столкновением водитель значительно превысил скорость.

Напоследок Алексей Жуган дал читателям пару цифр для размышления:

— Тормозной путь автомобиля, который едет со скоростью 60 км/ч, на сухом асфальте составляет около 25 метров, со скоростью 90 км/ч — 53 метра, то есть в два раза больше. И это без учета времени реакции водителя. Если скорость 150 км/ч, то тормозной путь составит 139 метров.

Источник