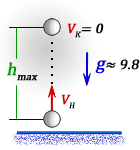
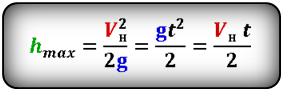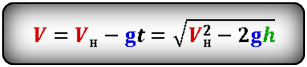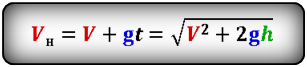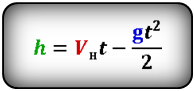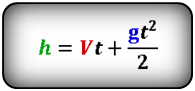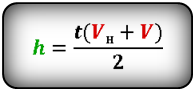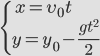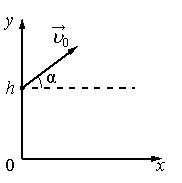1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
h max
— максимальная высота достигнутая телом за время t
Vк — конечная скорость тела на пике, равная нулю
Vн — начальная скорость тела
t — время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 — ускорение свободного падения
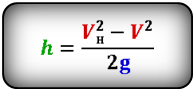
Формула максимальной высоты (h max):
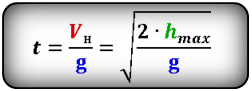
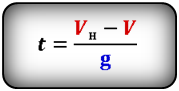
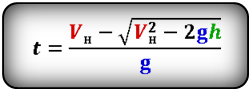
Формула времени за которое тело достигло максимальную высоту (t):
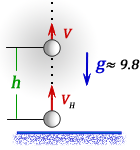
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
h — расстояние пройденное телом за время t
Vн — начальная скорость тела
V — скорость тела в момент времени t
t — время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула скорости тела в момент времени t (V):
Формула начальной скорости тела (Vн):
Формулы высоты тела в момент времени t (h):
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
- Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
- Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
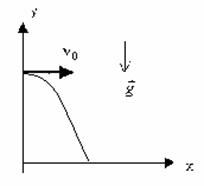
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
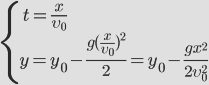
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
Решим задачу для случая х0=0 и y0=0.
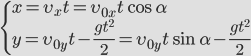
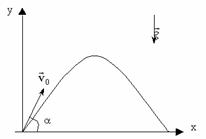
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
.
Мы получили квадратичную зависимость между координатами. Значит траектория — парабола.
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.
Время полета:


Зная время полета, найдем максимальное расстояние, которое пролетит тело:
Дальность полета:
Из этой формулы следует, что:
— максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450;
— на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.
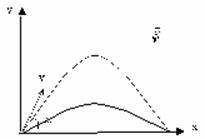
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно: 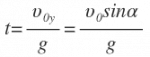
Время подъема:
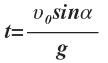
Тогда:
Максимальная высота:
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна
Угол, под которым направлен вектор скорости в любой момент времени:
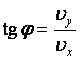
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты!График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Важные факты!
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
Уравнение координаты x:
x = v0 cosα t
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562
С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17980
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.
- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
Ответ: 42
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 43.4k
Рассмотрим тело, брошенное под углом к горизонту. Пусть сопротивление воздуха будет очень малой величиной, такой малой, что мы сможем ей пренебречь.
Благодаря силе притяжения земли тело часть пути будет подниматься над поверхностью, а часть – опускаться к поверхности. Траектория полета такого тела – это парабола (рис. 1).
Рис. 1. Парабола – это траектория тела, брошенного под углом к горизонту
Разложим скорость тела
Вместо того, чтобы рассматривать сложное движение одного тела по параболе, будем рассматривать одновременное и более простое движение двух тел. Одно тело движется по вертикали, а второе – по горизонтали. Тела одновременно стартуют и заканчивают движение.
Мы сможем сложное движение разделить на два простых, как только разложим на проекции скорость тела. Полученные скорости будем рассматривать, как скорости отдельно двигающихся тел.
Любой вектор, направленный под углом к осям, можно разложить на проекции — вертикальную и горизонтальную (рис. 2).
Рис. 2. Вектор начальной скорости тела раскладываем на проекции, после этого можно каждую проекцию рассматривать отдельно
Формулы разложения скорости выглядят так:
[ large boxed{ begin{cases} v_{0y} = v cdot sin(alpha) \ v_{0x} = v cdot cos(alpha) end{cases} } ]
Вертикальная и горизонтальная проекции скорости
Обратим внимание теперь на рисунок 3.
Рис. 3. Вертикальная часть скорости сначала уменьшается, а потом растет, а горизонтальная часть – не меняется
На рисунке черным цветом обозначен вектор скорости летящего тела. Видно, что от точки к точке он изменяется не только по модулю, но и по направлению. То есть, меняются характеристики вектора.
Вектор, обозначенный синим цветом на рисунке – это горизонтальная проекция вектора скорости. Заметно, что горизонтальная часть скорости не меняется ни по длине, ни по направлению, то есть, остается постоянной (одной и той же).
Вертикальная проекция скорости обозначена на рисунке красным цветом. При движении вверх она уменьшается, а при движении вниз – растет.
В самой высокой точке траектории вертикальная проекция скорости превращается в ноль. Из-за этого в верхней точке скорость направлена только горизонтально и равна числу ( v_{0x}). Число ( v_{0x}) – это горизонтальная проекция начальной скорости ( v_{0}) тела.
Упростить сложное движение тела на плоскости можно, рассматривая отдельно движение двух тел: одно тело движется по вертикали, меняя свою скорость, а второе – по горизонтали и, скорость свою не меняет.
Из рисунка 3 так же, следует, что
если тело при падении вернется на уровень, с которого оно стартовало, то:
- скорость, с которой мы подбросим тело, по модулю будет равна скорости, с которой тело упадет;
- угол (alpha) между скоростью тела на старте и осью Ox будет равен углу между конечной скоростью и горизонталью;
- время подъема равняется времени спуска;
Запишем теперь формулы, описывающие движение тела, под углом к горизонту. Разделим движение тела на две части: подъем и спуск. Вертикальное движение тела происходит под действием силы тяжести.
Подъем
Когда тело поднимается, оно проходит вертикальный путь (h):
[ large h = v_{0y} cdot t_{text{вверх}} — g cdot frac{t_{text{вверх}}^2}{2} ]
Вертикальная часть скорости уменьшается – движение равнозамедленное:
[ large v_{y} = v_{0y} — g cdot t_{text{вверх}} ]
Горизонтальная часть скорости остается такой же, как была в начале пути.
[ large v_{x} = v_{0x} ]
Поэтому вдоль горизонтали движение равномерное, т. е. происходит с неизменной скоростью
[ large S_{1} = v_{0x} cdot t_{text{вверх}}]
Эти формулы можно записать в виде системы:
[ large boxed{ begin{cases} v_{y} = v_{0y} — g cdot t_{text{вверх}} \ h = v_{0y} cdot t_{text{вверх}} — g cdot frac{t_{text{вверх}}^2}{2} \ S_{1} = v_{0x} cdot t_{text{вверх}} end{cases} } ]
На максимальной высоте траектории скорость имеет только горизонтальную проекцию (вертикальной скорости нет, скорость только горизонтальная).
[ large boxed{ begin{cases} h = h_{max} \ v_{y} = 0 \ v = v_{0x} end{cases} } ]
Спуск
При спуске, вертикальная проекция скорости растет – движение равноускоренное
[ large v_{y} = 0 + g cdot t_{text{вниз}} ] ,
Тело спускается, вертикальное перемещение можно найти из соотношения
[ large h = g cdot frac{t_{text{вниз}}^2}{2} ]
Горизонтальная часть скорости – все так же, меняться не будет. Поэтому движение вдоль горизонтали происходит с неизменной скоростью и тело проходит вторую часть горизонтального пути
[ large S_{2} = v_{0x} cdot t_{text{вниз}} ]
Объединим эти формулы в систему
[ large boxed{ begin{cases} v_{y} = 0 + g cdot t_{text{вниз}} \ h = g cdot frac{t_{text{вниз}}^2}{2} \ S_{2} = v_{0x} cdot t_{text{вниз}} end{cases} } ]
После того, как мы найдем время подъема и время спуска, можем найти общий путь по горизонтали:
[ large boxed{ S = S_{1} + S_{2} = v_{0x} cdot left(t_{text{вверх}} + t_{text{вниз}} right)}]
Считается, что высота объекта описывает движение, когда тело движется в вертикальном направлении. В этом случае высота переносится на расстояние, чтобы найти скорость.
Предположим, что какой-то предмет подброшен в воздух; используемый объект перемещается на определенной высоте и преодолевает определенное расстояние. В этом случае тело совершает как вертикальные, так и горизонтальные движения, в этом случае как рассчитать скорость по высоте и расстояние? Ответ обсуждается в этом посте.
Как найти скорость по высоте и расстоянию?
Когда объект проецируется вверх, он достигает определенной высоты и падает обратно на поверхность, преодолевая определенное расстояние. Скорость объекта должна быть рассчитана с использованием этих двух данных.
Скорость спроецированного объекта при движении вверх отличается от скорости того же объекта при движении вниз. Поскольку объект движется вертикально вверх, а после достижения максимальной высоты снова возвращается на землю, высота не равна расстоянию, как обсуждалось в предыдущей статье.
Поскольку объект перемещался как вверх, так и вниз, общее пройденное расстояние объектом задается
х = д + ч
Поскольку объект возвращается к земле на максимальной высоте h, пик, на котором объект увеличивает свою скорость, чтобы вернуться к земле, определяется как
Когда объект начинает падать с пика, высота уменьшается, поэтому общее расстояние, пройденное объектом, можно переписать как
Следовательно, полное расстояние, пройденное объектом, можно выразить как
Мы знаем, что из кинематического уравнения движения расстояние, пройденное телом, движущимся со скоростью v и начинающим ускоряться за каждые t секунд, определяется выражением;
Мы можем подставить полученное значение x в уравнение, чтобы получить скорость от высоты и расстояния как, чтобы получить
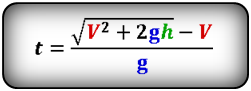
Переставляя условия, чтобы получить скорость как
Приведенное выше уравнение дает ответ на вопрос, как найти скорость по высоте и расстоянию.
Как найти начальную скорость, зная высоту и расстояние?
Мы уже обсуждали несколько способов нахождения начальной скорости. Ан ускоряющееся тело имеет различные значения скорости. Начальную скорость можно вычислить, используя ускорение, но можем ли мы вычислить Начальная скорость с высотой и расстоянием?
Начальная скорость тела рассчитывается при моменте времени t=0. В момент времени t=0 для нахождения скорости используются высота, на которой находится тело, и расстояние, которое оно преодолело. Ускоряющееся тело продолжает изменять скорость; это помогает нам найти начальную скорость.
Давайте рассмотрим пример; тело толкают с определенной высоты «h», оно начинает падать под определенным углом и перемещается на определенное расстояние по направлению вниз. При движении тела вниз его скорость становится максимальной из-за гравитационного притяжения.
В этом случае расстояние находится по горизонтальной плоскости, а высота по вертикальной плоскости.
Во-первых, мы имеем дело с высотой объекта, потому что высота — это сущность, на которую влияет гравитация. Уравнение для вертикального перемещения, т. е. высоты пройденного тела, имеет вид
Здесь мы используем ускорение за счет силы тяжести, потому что в вертикальном направлении тело может ускоряться только за счет силы тяжести.
При вертикальном движении считаем v=0, так как изначально тело обладает нулевая скорость.
Следовательно, по этому уравнению мы можем найти интервал времени t.
Мы можем найти начальную скорость при горизонтальном движении, так как тело также может ускоряться за счет фактора скорости.
Теперь у нас есть временной интервал, чтобы покрыть расстояние д. начальную скорость можно рассчитать как
Концепцию нахождения начальной скорости можно ясно понять, решая задачи, что делается в следующем разделе.
Как найти горизонтальную скорость по расстоянию и высоте?
Как правило, мы делим компоненты на вертикальное и горизонтальное движение при решении задач скорости. Перемещение тела по горизонтали направление за заданный период времени дает горизонтальную скорость.
Высота может влиять на скорость только тогда, когда тело движется в вертикальном направлении. Если тело совершает как вертикальное, так и горизонтальное движение, то нам нужна величина скорости для вычисления горизонтальной скорости. Узнаем, как найти скорость по высоте, учитывая расстояние, пройденное телом по горизонтали.
Горизонтальная составляющая скорости определяется выражением
vx= v cosθ
Вертикальная составляющая скорости определяется выражением
vy = vsinθ
Так как сила тяжести влияет на вертикальное движение тела, поэтому вертикальные компоненты могут быть выражены как
vy = vsinθ-gt
Скорость может быть выражена как
v = v.x + Vy
Величина скорости выражается как
Если тело достигает максимальной высоты, вертикальная скорость vy равен нулю. Его можно дать как
vy = 0 = vsinθ-gt
gt = v sinθ
Полное время полета тела равно 2t, поэтому, используя приведенное выше выражение, время можно представить как
g(t) = v sinθ
t=v sinθ/g
Предположим, что пробег тела при движении есть не что иное, как расстояние, пройденное телом; это может быть дано как
д=в2 sin2θ/г
Высота, достигнутая телом при вертикальном движении, определяется выражением
ч=(1/2)гт2
Подставляя значение временного интервала t, получаем,
Мы можем приравнять полученное уравнение высоты и расстояния, чтобы получить значение θ как
Но нам нужно найти горизонтальную скорость vx= vcosθ
Используя уравнение высоты и расстояния, мы можем вычислить значение v и, следовательно, подставив значение v в горизонтальную составляющую скорость уравнение мы получаем горизонтальная скорость.
Решенные примеры задач о том, как найти скорость с высотой и расстоянием
Найдите скорость снаряда, ускоряющегося под действием силы тяжести, летящего вверх, достигающего максимальной высоты 12 м и пролетающего расстояние 42 м. Время, за которое снаряд преодолевает расстояние, составляет 1.33 секунды.
Решение:
Дано – максимальная высота, достигнутая снарядом h = 12м.
Путь, пройденный снарядом d = 42м.
Время, за которое снаряд пролетит заданное расстояние t = 1.33 с.
Ускорение свободного падения g = 9.8 м/с.2.
Скорость для заданной высоты и расстояния определяется выражением
v = 11.27 -6.527
v = 4.743 м / с
Камень брошен горизонтально с вершины холма на высоту 12 м и расстояние, пройденное камнем в горизонтальном направлении, равно 23 м. Если камень ускоряется под действием силы тяжести, как найти скорость, зная высоту и расстояние?
Решение:
Дано – высота, на которую брошен камень h = 12м.
Горизонтальное расстояние, пройденное камнем d = 23 м.
Ускорение свободного падения g = 9.8 м/с.2.
Поскольку камень брошен горизонтально, его вертикальная скорость изначально равна нулю. Время, необходимое для преодоления заданного расстояния, определяется выражением
Чтобы найти скорость, общее выражение дается выражением
v=d/t
v = 23/1.56
v=14.74 м/с.
Найти горизонтальную скорость тела, брошенного вертикально на высоту 6 м и пройденного по горизонтали 17 м. (Примите ускорение свободного падения 10 м/с.2)
Решение:
Дано – горизонтальный путь, пройденный телом d= 17м.
Высота по вертикали h = 6м.
Горизонтальная скорость определяется выражением
vx = v cosθ
Значение тета для горизонтальной скорости задается тангенсом-1(2) = 63.43
v2=17/[10sin2(63.43)]
v2= 0.768
v=0.876 м/с.
Найдите начальную скорость тела, если оно движется с ускорением 5 м/с.2 и расстояние, пройденное объектом, составляет 13 метров, а высота, на которой он движется, составляет 4 метра над землей.
Решение:
Дано – ускорение тела a = 5м/с2.
Расстояние, пройденное объектом d = 13м.
Высота объекта h = 4м.
Изначально вертикаль. скорость объекта равна нулю и, следовательно, уравнение можно записать в виде
t2 = 1.6
t= 1.26 с.
Начальная скорость может быть задана как
vi= д / т
vi= 13 / 1.26
vi = 10.31 м / с.