Синус угла. Таблица синусов.
Синус угла через градусы, минуты и секунды
Синус угла через десятичную запись угла
Как найти угол зная синус этого угла
У синуса есть обратная тригонометрическая функция — arcsin(y)=x
Пример sin(30°) = 1/2; arcsin(1/2) = 30°
Определение синуса
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
Периодичность синуса
Функция y = sin(x) периодична, с периодом 2π
Теорема синусов
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
На b сокращаем, синусы переносим в знаменатели:
bc sinα = ca sinβ
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
- Стороны треугольника, если даны два угла и одна сторона.
- Углы треугольника, если даны две стороны и один прилежащий угол.
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Следовательно, ∠А1 = 180° — α.
Вспомним свойство вписанного в окружность четырёхугольника:
Также известно, что sin(180° — α) = sinα.
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
α = 2R sin (180° — α) = 2R sinα
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
- sin120° = sin(180° — 60°) = sin60° = 3/√2;
- sin150° = sin(180° — 30°) = sin30° = 1/2;
- sin135° = sin(180° — 45°) = sin45° = 2/√2.
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Поэтому: ∠A + ∠C = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
sinγ = sin(180° — α)
Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
-
Согласно теореме о сумме углов треугольника:
∠B = 180° — 45° — 15° = 120°
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>
Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
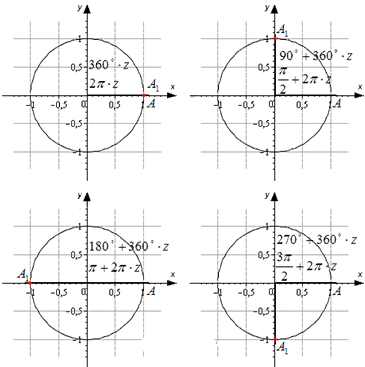
Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z — любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.
Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) . Мы находим значения всех функций кроме тангенса.
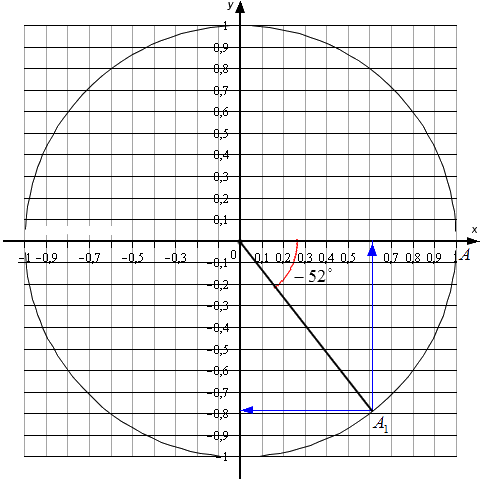
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( — 52 ° ) ≈ — 0 , 78 и cos ( — 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: t g ( — 52 ° ) ≈ — 0 , 78 0 , 62 ≈ — 1 , 26 и c t g ( — 52 ° ) ≈ 0 , 62 — 0 , 78 ≈ — 0 , 79 .
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
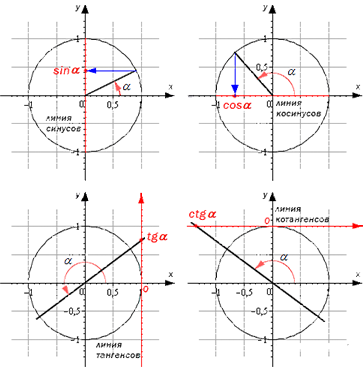
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α , cos α , t g α , c t g α
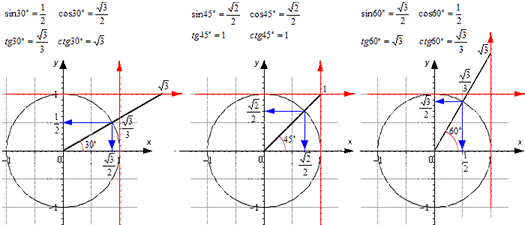
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 — 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 . Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .
Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .
Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 — 1 .
Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 — 1 = 2 + 1 ( 2 — 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 — 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α . Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 — 2 2 · ( 2 + 2 ) · ( 2 — 2 ) = = 2 — 2 2 · ( 2 2 — ( 2 ) 2 ) = 2 — 2 4
Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 — 2 4 = 2 — 2 2 . sin π 8 = 2 — 2 2 .
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = — sin 30 ° = — 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° — 60 ° ) = — cos 60 ° = — 1 2 .
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение t g π 8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 — cos π 4 1 + cos π 4 . Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 — cos π 4 1 + cos π 4 = 1 — 2 2 1 + 2 2 = 2 — 2 2 + 2 = = ( 2 — 2 ) 2 ( 2 + 2 ) · ( 2 — 2 ) = ( 2 — 2 ) 2 2 2 — ( 2 ) 2 = ( 2 — 2 ) 2 2
Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 — 2 ) 2 2 = 2 — 2 2 = 2 — 1
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
http://skysmart.ru/articles/mathematic/teorema-sinusov
http://zaochnik.com/spravochnik/matematika/trigonometrija/nahozhdenie-znachenij-sinusa-kosinusa-tangensa-i-k/
Синус угла. Таблица синусов.
Синус угла через градусы, минуты и секунды
Синус угла через десятичную запись угла
Как найти угол зная синус этого угла
У синуса есть обратная тригонометрическая функция — arcsin(y)=x
sin(arcsin(y))=y
Пример sin(30°) = 1/2; arcsin(1/2) = 30°
Рассчитать арксинус
Определение синуса
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
sin(α) = BC/AB
sin(-α) = -sin(α)
Периодичность синуса
Функция y = sin(x) периодична, с периодом 2π
sin(α ± 2π) = sin(α)
Пример sin(5π) = sin(4π + π) = sin(π)
Таблица синусов в радианах
sin(0°) = 0sin(π/12) = sin(15°) = 0.2588190451sin(π/6) = sin(30°) = 0.5sin(π/4) = sin(45°) = 0.7071067812sin(π/3) = sin(60°) = 0.8660254038sin(5π/12) = sin(75°) = 0.9659258263sin(π/2) = sin(90°) = 1sin(7π/12) = sin(105°) = 0.9659258263sin(2π/3) = sin(120°) = 0.8660254038sin(3π/4) = sin(135°) = 0.7071067812sin(5π/6) = sin(150°) = 0.5sin(11π/12) = sin(165°) = 0.2588190451sin(π) = sin(180°) = 0sin(13π/12) = sin(195°) = -0.2588190451sin(7π/6) = sin(210°) = -0.5sin(5π/4) = sin(225°) = -0.7071067812sin(4π/3) = sin(240°) = -0.8660254038sin(17π/12) = sin(255°) = -0.9659258263sin(3π/2) = sin(270°) = -1sin(19π/12) = sin(285°) = -0.9659258263sin(5π/3) = sin(300°) = -0.8660254038sin(7π/4) = sin(315°) = -0.7071067812sin(11π/6) = sin(330°) = -0.5sin(23π/12) = sin(345°) = -0.2588190451
Таблица Брадиса синусы
| sin(0) = 0 | sin(120) = 0.8660254038 | sin(240) = -0.8660254038 |
| sin(1) = 0.01745240644 | sin(121) = 0.8571673007 | sin(241) = -0.8746197071 |
| sin(2) = 0.0348994967 | sin(122) = 0.8480480962 | sin(242) = -0.8829475929 |
| sin(3) = 0.05233595624 | sin(123) = 0.8386705679 | sin(243) = -0.8910065242 |
| sin(4) = 0.06975647374 | sin(124) = 0.8290375726 | sin(244) = -0.8987940463 |
| sin(5) = 0.08715574275 | sin(125) = 0.8191520443 | sin(245) = -0.906307787 |
| sin(6) = 0.1045284633 | sin(126) = 0.8090169944 | sin(246) = -0.9135454576 |
| sin(7) = 0.1218693434 | sin(127) = 0.79863551 | sin(247) = -0.9205048535 |
| sin(8) = 0.139173101 | sin(128) = 0.7880107536 | sin(248) = -0.9271838546 |
| sin(9) = 0.156434465 | sin(129) = 0.7771459615 | sin(249) = -0.9335804265 |
| sin(10) = 0.1736481777 | sin(130) = 0.7660444431 | sin(250) = -0.9396926208 |
| sin(11) = 0.1908089954 | sin(131) = 0.7547095802 | sin(251) = -0.9455185756 |
| sin(12) = 0.2079116908 | sin(132) = 0.7431448255 | sin(252) = -0.9510565163 |
| sin(13) = 0.2249510543 | sin(133) = 0.7313537016 | sin(253) = -0.956304756 |
| sin(14) = 0.2419218956 | sin(134) = 0.7193398003 | sin(254) = -0.9612616959 |
| sin(15) = 0.2588190451 | sin(135) = 0.7071067812 | sin(255) = -0.9659258263 |
| sin(16) = 0.2756373558 | sin(136) = 0.6946583705 | sin(256) = -0.9702957263 |
| sin(17) = 0.2923717047 | sin(137) = 0.6819983601 | sin(257) = -0.9743700648 |
| sin(18) = 0.3090169944 | sin(138) = 0.6691306064 | sin(258) = -0.9781476007 |
| sin(19) = 0.3255681545 | sin(139) = 0.656059029 | sin(259) = -0.9816271834 |
| sin(20) = 0.3420201433 | sin(140) = 0.6427876097 | sin(260) = -0.984807753 |
| sin(21) = 0.3583679495 | sin(141) = 0.629320391 | sin(261) = -0.9876883406 |
| sin(22) = 0.3746065934 | sin(142) = 0.6156614753 | sin(262) = -0.9902680687 |
| sin(23) = 0.3907311285 | sin(143) = 0.6018150232 | sin(263) = -0.9925461516 |
| sin(24) = 0.4067366431 | sin(144) = 0.5877852523 | sin(264) = -0.9945218954 |
| sin(25) = 0.4226182617 | sin(145) = 0.5735764364 | sin(265) = -0.9961946981 |
| sin(26) = 0.4383711468 | sin(146) = 0.5591929035 | sin(266) = -0.9975640503 |
| sin(27) = 0.4539904997 | sin(147) = 0.544639035 | sin(267) = -0.9986295348 |
| sin(28) = 0.4694715628 | sin(148) = 0.5299192642 | sin(268) = -0.999390827 |
| sin(29) = 0.4848096202 | sin(149) = 0.5150380749 | sin(269) = -0.9998476952 |
| sin(30) = 0.5 | sin(150) = 0.5 | sin(270) = -1 |
| sin(31) = 0.5150380749 | sin(151) = 0.4848096202 | sin(271) = -0.9998476952 |
| sin(32) = 0.5299192642 | sin(152) = 0.4694715628 | sin(272) = -0.999390827 |
| sin(33) = 0.544639035 | sin(153) = 0.4539904997 | sin(273) = -0.9986295348 |
| sin(34) = 0.5591929035 | sin(154) = 0.4383711468 | sin(274) = -0.9975640503 |
| sin(35) = 0.5735764364 | sin(155) = 0.4226182617 | sin(275) = -0.9961946981 |
| sin(36) = 0.5877852523 | sin(156) = 0.4067366431 | sin(276) = -0.9945218954 |
| sin(37) = 0.6018150232 | sin(157) = 0.3907311285 | sin(277) = -0.9925461516 |
| sin(38) = 0.6156614753 | sin(158) = 0.3746065934 | sin(278) = -0.9902680687 |
| sin(39) = 0.629320391 | sin(159) = 0.3583679495 | sin(279) = -0.9876883406 |
| sin(40) = 0.6427876097 | sin(160) = 0.3420201433 | sin(280) = -0.984807753 |
| sin(41) = 0.656059029 | sin(161) = 0.3255681545 | sin(281) = -0.9816271834 |
| sin(42) = 0.6691306064 | sin(162) = 0.3090169944 | sin(282) = -0.9781476007 |
| sin(43) = 0.6819983601 | sin(163) = 0.2923717047 | sin(283) = -0.9743700648 |
| sin(44) = 0.6946583705 | sin(164) = 0.2756373558 | sin(284) = -0.9702957263 |
| sin(45) = 0.7071067812 | sin(165) = 0.2588190451 | sin(285) = -0.9659258263 |
| sin(46) = 0.7193398003 | sin(166) = 0.2419218956 | sin(286) = -0.9612616959 |
| sin(47) = 0.7313537016 | sin(167) = 0.2249510543 | sin(287) = -0.956304756 |
| sin(48) = 0.7431448255 | sin(168) = 0.2079116908 | sin(288) = -0.9510565163 |
| sin(49) = 0.7547095802 | sin(169) = 0.1908089954 | sin(289) = -0.9455185756 |
| sin(50) = 0.7660444431 | sin(170) = 0.1736481777 | sin(290) = -0.9396926208 |
| sin(51) = 0.7771459615 | sin(171) = 0.156434465 | sin(291) = -0.9335804265 |
| sin(52) = 0.7880107536 | sin(172) = 0.139173101 | sin(292) = -0.9271838546 |
| sin(53) = 0.79863551 | sin(173) = 0.1218693434 | sin(293) = -0.9205048535 |
| sin(54) = 0.8090169944 | sin(174) = 0.1045284633 | sin(294) = -0.9135454576 |
| sin(55) = 0.8191520443 | sin(175) = 0.08715574275 | sin(295) = -0.906307787 |
| sin(56) = 0.8290375726 | sin(176) = 0.06975647374 | sin(296) = -0.8987940463 |
| sin(57) = 0.8386705679 | sin(177) = 0.05233595624 | sin(297) = -0.8910065242 |
| sin(58) = 0.8480480962 | sin(178) = 0.0348994967 | sin(298) = -0.8829475929 |
| sin(59) = 0.8571673007 | sin(179) = 0.01745240644 | sin(299) = -0.8746197071 |
| sin(60) = 0.8660254038 | sin(180) = 0 | sin(300) = -0.8660254038 |
| sin(61) = 0.8746197071 | sin(181) = -0.01745240644 | sin(301) = -0.8571673007 |
| sin(62) = 0.8829475929 | sin(182) = -0.0348994967 | sin(302) = -0.8480480962 |
| sin(63) = 0.8910065242 | sin(183) = -0.05233595624 | sin(303) = -0.8386705679 |
| sin(64) = 0.8987940463 | sin(184) = -0.06975647374 | sin(304) = -0.8290375726 |
| sin(65) = 0.906307787 | sin(185) = -0.08715574275 | sin(305) = -0.8191520443 |
| sin(66) = 0.9135454576 | sin(186) = -0.1045284633 | sin(306) = -0.8090169944 |
| sin(67) = 0.9205048535 | sin(187) = -0.1218693434 | sin(307) = -0.79863551 |
| sin(68) = 0.9271838546 | sin(188) = -0.139173101 | sin(308) = -0.7880107536 |
| sin(69) = 0.9335804265 | sin(189) = -0.156434465 | sin(309) = -0.7771459615 |
| sin(70) = 0.9396926208 | sin(190) = -0.1736481777 | sin(310) = -0.7660444431 |
| sin(71) = 0.9455185756 | sin(191) = -0.1908089954 | sin(311) = -0.7547095802 |
| sin(72) = 0.9510565163 | sin(192) = -0.2079116908 | sin(312) = -0.7431448255 |
| sin(73) = 0.956304756 | sin(193) = -0.2249510543 | sin(313) = -0.7313537016 |
| sin(74) = 0.9612616959 | sin(194) = -0.2419218956 | sin(314) = -0.7193398003 |
| sin(75) = 0.9659258263 | sin(195) = -0.2588190451 | sin(315) = -0.7071067812 |
| sin(76) = 0.9702957263 | sin(196) = -0.2756373558 | sin(316) = -0.6946583705 |
| sin(77) = 0.9743700648 | sin(197) = -0.2923717047 | sin(317) = -0.6819983601 |
| sin(78) = 0.9781476007 | sin(198) = -0.3090169944 | sin(318) = -0.6691306064 |
| sin(79) = 0.9816271834 | sin(199) = -0.3255681545 | sin(319) = -0.656059029 |
| sin(80) = 0.984807753 | sin(200) = -0.3420201433 | sin(320) = -0.6427876097 |
| sin(81) = 0.9876883406 | sin(201) = -0.3583679495 | sin(321) = -0.629320391 |
| sin(82) = 0.9902680687 | sin(202) = -0.3746065934 | sin(322) = -0.6156614753 |
| sin(83) = 0.9925461516 | sin(203) = -0.3907311285 | sin(323) = -0.6018150232 |
| sin(84) = 0.9945218954 | sin(204) = -0.4067366431 | sin(324) = -0.5877852523 |
| sin(85) = 0.9961946981 | sin(205) = -0.4226182617 | sin(325) = -0.5735764364 |
| sin(86) = 0.9975640503 | sin(206) = -0.4383711468 | sin(326) = -0.5591929035 |
| sin(87) = 0.9986295348 | sin(207) = -0.4539904997 | sin(327) = -0.544639035 |
| sin(88) = 0.999390827 | sin(208) = -0.4694715628 | sin(328) = -0.5299192642 |
| sin(89) = 0.9998476952 | sin(209) = -0.4848096202 | sin(329) = -0.5150380749 |
| sin(90) = 1 | sin(210) = -0.5 | sin(330) = -0.5 |
| sin(91) = 0.9998476952 | sin(211) = -0.5150380749 | sin(331) = -0.4848096202 |
| sin(92) = 0.999390827 | sin(212) = -0.5299192642 | sin(332) = -0.4694715628 |
| sin(93) = 0.9986295348 | sin(213) = -0.544639035 | sin(333) = -0.4539904997 |
| sin(94) = 0.9975640503 | sin(214) = -0.5591929035 | sin(334) = -0.4383711468 |
| sin(95) = 0.9961946981 | sin(215) = -0.5735764364 | sin(335) = -0.4226182617 |
| sin(96) = 0.9945218954 | sin(216) = -0.5877852523 | sin(336) = -0.4067366431 |
| sin(97) = 0.9925461516 | sin(217) = -0.6018150232 | sin(337) = -0.3907311285 |
| sin(98) = 0.9902680687 | sin(218) = -0.6156614753 | sin(338) = -0.3746065934 |
| sin(99) = 0.9876883406 | sin(219) = -0.629320391 | sin(339) = -0.3583679495 |
| sin(100) = 0.984807753 | sin(220) = -0.6427876097 | sin(340) = -0.3420201433 |
| sin(101) = 0.9816271834 | sin(221) = -0.656059029 | sin(341) = -0.3255681545 |
| sin(102) = 0.9781476007 | sin(222) = -0.6691306064 | sin(342) = -0.3090169944 |
| sin(103) = 0.9743700648 | sin(223) = -0.6819983601 | sin(343) = -0.2923717047 |
| sin(104) = 0.9702957263 | sin(224) = -0.6946583705 | sin(344) = -0.2756373558 |
| sin(105) = 0.9659258263 | sin(225) = -0.7071067812 | sin(345) = -0.2588190451 |
| sin(106) = 0.9612616959 | sin(226) = -0.7193398003 | sin(346) = -0.2419218956 |
| sin(107) = 0.956304756 | sin(227) = -0.7313537016 | sin(347) = -0.2249510543 |
| sin(108) = 0.9510565163 | sin(228) = -0.7431448255 | sin(348) = -0.2079116908 |
| sin(109) = 0.9455185756 | sin(229) = -0.7547095802 | sin(349) = -0.1908089954 |
| sin(110) = 0.9396926208 | sin(230) = -0.7660444431 | sin(350) = -0.1736481777 |
| sin(111) = 0.9335804265 | sin(231) = -0.7771459615 | sin(351) = -0.156434465 |
| sin(112) = 0.9271838546 | sin(232) = -0.7880107536 | sin(352) = -0.139173101 |
| sin(113) = 0.9205048535 | sin(233) = -0.79863551 | sin(353) = -0.1218693434 |
| sin(114) = 0.9135454576 | sin(234) = -0.8090169944 | sin(354) = -0.1045284633 |
| sin(115) = 0.906307787 | sin(235) = -0.8191520443 | sin(355) = -0.08715574275 |
| sin(116) = 0.8987940463 | sin(236) = -0.8290375726 | sin(356) = -0.06975647374 |
| sin(117) = 0.8910065242 | sin(237) = -0.8386705679 | sin(357) = -0.05233595624 |
| sin(118) = 0.8829475929 | sin(238) = -0.8480480962 | sin(358) = -0.0348994967 |
| sin(119) = 0.8746197071 | sin(239) = -0.8571673007 | sin(359) = -0.01745240644 |
Похожие калькуляторы
Построение тригонометрической окружности
А теперь сделай вот что: возьми-ка в руки циркуль и нарисуй любую (самую любую, но лучше достаточно немаленькую) окружность.
Получилось?
Ну да ладно, задачка не самая сложная. Так, ты не потерял ту точку, в которой у тебя был центр (куда ты прикладывал острую ножку циркуля)? Я вот у себя потерял, растяпа! Ну ладно, найду!
А что пока делать тебе?
А вот что: проведи через эту точку две линии, которые пересекаются «прямым крестиком», то есть под прямым углом. И пусть их точка пересечения – это центр (который ты не потерял!) окружности.
Нарисовал? У меня получилось что-то вроде вот этого.
Правда я чуть-чуть поторопился и сразу «обозвал» эти прямые ( displaystyle x) и ( displaystyle y) и точку пересечения через ( displaystyle O).
А что такое в таком случае ( displaystyle R)?
Это радиус нашей окружности.
Как называлась наша тема? Единичная окружность.
Тогда будем считать ( но не будем так рисовать!), что ( displaystyle R=1 ).
А рисовать мы так не будем, потому что на такой крошечной картинке ты ничего не разберешь! Ты же понимаешь, что когда инженеры проектируют самолеты, скажем, они не рисуют его в натуральную величину?
Так и мы не будем рисовать единичную окружность в самом деле единичной. Это нам нужно исключительно для удобства.
Теперь отмечаем: ( displaystyle OR=1). Что же мы с тобой на самом деле сделали? А вот что:
Мы поместили нашу окружность в систему координат ( displaystyle mathbf{X0Y}), сделав центр окружности началом координат!
Это позволит изучать свойства такой окружности уже не с геометрической, а с математической точки зрения. Этот подход был придуман хитрым математиком и философом Рене Декартом еще в 17 веке!
Перегнать фигуру в цифры, каково, а?
Но допустим, мы поместили нашу окружность в координаты. В скольких точках она пересекается с осями системы координат?
В четырех. Вот они:
Эти точки ( displaystyle left( A; B; C; D right)) имеют координаты:
( displaystyle Aleft( 1,0 right)); ( displaystyle Bleft( 0,1 right)); ( displaystyle Cleft( -1;0 right)); ( displaystyle Dleft( 0;-1 right)).
Теперь вспомни, как называются области, на которые этот «координатный крестик» делит всю плоскость?
Они называются координатные четверти.
Тогда посмотри на рисунок. Наша окружность тоже оказалась разрезанной на 4 равные дольки. Давай пронумеруем каждую из этих долек против часовой стрелки:
Ты уже можешь догадаться, как называются эти самые дольки:
1 четверть, 2 четверть, 3 четверть, 4 четверть
(Прямо как четверти в школе!)
Углы на тригонометрической окружности
Теперь давай сделаем еще вот что. Снова посмотрим на предыдущую картинку.
Чему на ней равен ( displaystyle angle AOB)?
Он равен ( displaystyle 90{}^circ ).
Также, как и ( displaystyle angle BOC), как и угол ( displaystyle angle COD), и угол ( displaystyle angle DOA).
( displaystyle angle text{AOB}=angle text{BOC}=angle text{COD}=angle text{DOA}=90{}^circ )
Тогда чему равна их сумма?
Она равна ( displaystyle 360{}^circ ).
Вместе же эти 4 угла составляют всю окружность целиком!
Градусная мера окружности равна ( displaystyle 360{}^circ )!
( displaystyle angle Atext{OC}=angle text{AOB}+angle text{BOC}=180{}^circ )
Что еще можно вытянуть? А вот что:
( displaystyle angle Atext{OD}=angle text{AOB}+angle text{BOC}+angle text{COD}=270{}^circ )
Отметим эти значения также на нашей окружности:
Однако, ты нередко можешь увидеть и вот такую картинку:
где вместо привычных нам градусов появляются некие буковки «пи» ( displaystyle pi ) с цифрами.
В чем же тут дело, кто прав и кто виноват?
Ну так вот, кто прав, кто виноват, решать, увы, не нам. Но чтобы «воз не был поныне там», нам нужно уделить этому моменту пару минут времени.
В самом деле, есть два способа измерять углы:
- Через градусы
- Через радианы
Как измерять углы через градусы мы все знаем. Это нам привычно. Однако в некоторых случаях их измеряют по-другому (как в градуснике есть несколько шкал: цельсий, кельвин, фаренгейт и т. д.), а именно: через радианы.
Для того, чтобы перейти от одной формы записи к другой, используется вот такое основное соотношение:
( displaystyle 180{}^circ =pi ~рад.)
И все, больше знать ничего не надо!
По пропорции ты легко получишь, что для того, чтобы пересчитать угол из градусов в радианы, нужно применить вот такую незамысловатую формулу:
( displaystyle P~рад.=frac{alpha {}^circ cdot pi }{180})
И наоборот: от радиан к градусам:
( displaystyle alpha {}^circ =frac{P~рад.cdot 180}{pi })
Ты должен уметь ориентироваться и в той, и в другой форме записи.
Потренируйся на следующих примерах:
- Перевести угол в ( displaystyle 30) градусов в радианы;
- Перевести угол ( displaystyle frac{pi }{4}) радиан в градусы;
- Перевести угол в ( displaystyle 60) градусов в радианы;
- Перевести угол в ( displaystyle frac{pi }{2}) радиан в градусы;
- Перевести угол в ( displaystyle 120) градусов в радианы;
- Перевести угол в ( displaystyle frac{3pi }{4}) радиан в градусы;
- Перевести угол в ( displaystyle 150) градусов в радианы.
Я сделаю только первые два, а остальные реши сам!
- ( P~рад.=frac{30cdot pi }{180}=frac{pi }{6}), тогда угол в ( displaystyle 30) градусов равен углу в ( displaystyle frac{pi }{6}) радиан;
- ( alpha {}^circ =frac{frac{pi }{4}cdot 180}{pi }=frac{45pi }{pi }=45{}^circ ), тогда угол в ( displaystyle frac{pi }{4}) радиан равен углу в ( displaystyle 45) градусов.
Все очень просто, не так ли? Остальные значения ты можешь найти в следующей таблице:
| ( displaystyle 0{}^circ ) | ( displaystyle 30{}^circ ) | ( displaystyle 45{}^circ ) | ( displaystyle 60{}^circ ) | ( displaystyle 90{}^circ ) | ( displaystyle 120{}^circ ) | ( displaystyle 135{}^circ ) | ( displaystyle 150{}^circ ) | ( displaystyle 180{}^circ ) |
| ( displaystyle 0) | ( displaystyle frac{pi }{6}) | ( displaystyle frac{pi }{4}) | ( displaystyle frac{pi }{3}) | ( displaystyle frac{pi }{2}) | ( displaystyle frac{2pi }{3}) | ( displaystyle frac{3pi }{4}) | ( displaystyle frac{5pi }{6}) | ( displaystyle pi ) |
| ( displaystyle 210{}^circ ) | ( displaystyle 225{}^circ ) | ( displaystyle 240{}^circ ) | ( displaystyle 270{}^circ ) | ( displaystyle 300{}^circ ) | ( displaystyle 315{}^circ ) | ( displaystyle 330{}^circ ) | ( displaystyle 360{}^circ ) |
| ( displaystyle frac{7pi }{6}) | ( displaystyle frac{5pi }{4}) | ( displaystyle frac{4pi }{3}) | ( displaystyle frac{3pi }{2}) | ( displaystyle frac{5pi }{3}) | ( displaystyle frac{7pi }{4}) | ( displaystyle frac{11pi }{6}) | ( displaystyle 2pi ) |
Так что впредь не удивляйся, когда ты увидишь вместо привычных градусов углы в радианах. Теперь ты знаешь, что это такое, и с чем его едят!
Синус, косинус, тангенс и котангенс на тригонометрической окружности
Но мы с тобой и так слишком увлеклись. Ты давно уже, наверное, заждался обещанных синусов и косинусов на тригонометрической окружности. Не смею более отвлекаться!
Давай сделаем вот что: совместим два знакомых нам объекта: тригонометрическую окружность (пока в том виде, в котором она у нас есть) и прямоугольный треугольник.
Что нам нужно, чтобы наш треугольник «целиком влез» в окружность?
Его гипотенуза должна быть не более единицы. Пусть же она у нас в точности будет равна единице.
Совместим мы их вот так:
Я нарисовал прямоугольный треугольник с центром в начале координат и гипотенузой равной ( 1). Это так потому, что окружность-то у меня единичная!
Тогда по определению синуса и косинуса:
- ( sin alpha =frac{AB}{OB}=frac{AB}{1}=AB)
- ( cos alpha =frac{OA}{OB}=frac{OA}{1}=OA)
А что же такое отрезки ( OA) и ( OB)? Чему равны их длины?
Смотри, сейчас будет самое главное: мы взяли угол ( alpha ) и провели луч, соединяющий этот угол с точкой на окружности.
Обозначим эту точку через ( B). Пусть ( B) имеет координаты ( Bleft( x,y right)).
Тогда длина отрезка ( OA) равна ( x), а длина отрезка ( AB)–равна ( y).
Но мы с тобой помним, что ( sin alpha =AB), ( cos alpha =OA), тогда:
- ( y=sin alpha )
- ( x=cos alpha )
Ух ты! Это надо еще раз обдумать, что же мы такое получили.
Давай проговорим еще раз: мы выбрали некоторый угол ( alpha ) и хотим найти его синус и косинус.
Что мы делаем?
- Проводим единичную окружность с центром, совпадающим с вершиной угла;
- Ищем точку пересечения нашего угла с окружностью;
- Её «иксовая» координата – это косинус нашего угла;
- Её «игрековая» координата – это синус нашего угла.
Вот и все! Теперь синус и косинус искать стало намного проще! Допустим, мы хотим найти синус, косинус ( 30) градусов.
Отмечаем ( 30) градусов на окружности и «достраиваем» этот угол до треугольника (как показано на рисунке выше).
Как найти ( x) и ( y)?
Да очень просто: в прямоугольном треугольнике катет, лежащий против угла в ( 30) градусов равен половине гипотенузы (это известный факт из геометрии 7 класса).
Так как гипотенуза равна ( 1), то противолежащий ей катет равен ( 0,5), откуда:
( sin 30{}^circ =0,5)
Что касается косинуса: для этого нам потребуется заметить, что выполняется тривиальное утверждение (основное тригонометрическое тождество):
( si{{n}^{2}}alpha +co{{s}^{2}}alpha =1)
Как ты думаешь, откуда оно берется? Да это же пресловутая теорема Пифагора!
Наши катеты в треугольничке равны ( x) и ( y), которые в свою очередь совпадают с ( cos alpha ) и ( sin alpha ). Гипотенуза в треугольнике равна ( 1).
Тогда:
( {{x}^{2}}+{{y}^{2}}=1) или, что то же самое,
( si{{n}^{2}}alpha +co{{s}^{2}}alpha =1)
Эта формула позволит по известному синусу вычислить неизвестный косинус и наоборот.
В частности, если:
( si{{n}^{2}}30{}^circ +co{{s}^{2}}30{}^circ =1) и ( sin 30{}^circ =0,5), то
( frac{1}{4}+co{{s}^{2}}30{}^circ =1)
( displaystyle co{{s}^{2}}30{}^circ =frac{3}{4})
( displaystyle cos 30{}^circ =pm sqrt{frac{3}{4}}=pm frac{sqrt{3}}{2})
Определение знака синуса, косинуса, тангенса и котангенса
Вообще, этот вопрос заслуживает особого внимания, но здесь все просто: у угла ( displaystyle 30) градусов и синус и косинус положительны (смотри рисунок), тогда берем знак «плюс».
( displaystyle cos 30{}^circ =frac{sqrt{3}}{2})
Теперь попробуй на основе вышеизложенного найти синус и косинус углов: ( displaystyle 60{}^circ ) и ( displaystyle 45{}^circ )
Можно схитрить: в частности для угла в ( displaystyle 60{}^circ ) градусов. Так как если один угол прямоугольного треугольника равен ( displaystyle 60{}^circ ) градусам, то второй – ( displaystyle 30{}^circ ) градусам. Теперь вступают в силу знакомые тебе формулы:
( displaystyle sin 30{}^circ =cos 60{}^circ )
( displaystyle sin 60{}^circ =cos 30{}^circ )
Тогда так как ( displaystyle sin 30{}^circ =0,5), то и ( displaystyle cos 60{}^circ =0,5). Так как ( displaystyle cos 30{}^circ =frac{sqrt{3}}{2}), то и ( displaystyle sin 60{}^circ =frac{sqrt{3}}{2}).
C ( displaystyle 45) градусами все еще проще: так если один из углов прямоугольного треугольника равен ( displaystyle 45) градусам, то и другой тоже равен ( displaystyle 45) градусам, а значит такой треугольник равнобедренный.
Значит, его катеты равны. А значит равны его синус и косинус.
Тогда:
( displaystyle si{{n}^{2}}45{}^circ +co{{s}^{2}}45{}^circ =2si{{n}^{2}}45{}^circ =1)
( displaystyle si{{n}^{2}}45{}^circ =co{{s}^{2}}45{}^circ =1/2)
Откуда: ( displaystyle sin 45{}^circ =cos 45{}^circ =sqrt{1/2}=frac{sqrt{2}}{2})
Теперь найди сам по новому определению (через икс и игрек!) синус и косинус углов в ( displaystyle 0) градусов и ( displaystyle 90) градусов. Здесь уже никакие треугольники нарисовать не получится! Уж слишком они будут плоские!
У тебя должно было получиться:
( displaystyle sin 0{}^circ =0), ( displaystyle cos 0{}^circ =1), ( displaystyle sin 90{}^circ =1), ( displaystyle cos 90{}^circ =0).
Тангенс и котангенс ты можешь отыскать самостоятельно по формулам:
( displaystyle text{t}g alpha =frac{sin alpha }{cos alpha }), ( displaystyle ctg alpha =frac{cos alpha }{sin alpha })
Обрати внимание, что на ноль делить нельзя!!
Теперь все полученные числа можно свести в таблицу:
Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти.
Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса ( displaystyle 90) градусов. Это неспроста!
В частности:
( displaystyle ctg 0=frac{cos 0}{sin 0}=frac{1}{0}=?????)
Поэтому мы с тобой будем считать, что тангенс ( displaystyle 90) градусов и котангенс нуля просто-напросто не определены!
Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая:
- Угол лежит в пределах от ( displaystyle 0) до ( displaystyle 360) градусов;
- Угол больше ( displaystyle 360) градусов.
Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае.
Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали.
Теперь же пусть наш угол больше ( displaystyle 90) градусов и не больше чем ( displaystyle 360).
Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти.
Как мы поступаем? Да точно так же!
Давай рассмотрим вместо вот такого случая…
…вот такой:
То есть рассмотрим угол ( displaystyle alpha ), лежащий во второй четверти. Что мы можем сказать про него?
У точки ( displaystyle {{M}_{1}}), которая является точкой пересечения луча и окружности по-прежнему имеет 2 координаты (ничего сверхъестественного, правда?). Это координаты ( displaystyle {{x}_{1}}) и ( displaystyle {{y}_{1}}).
Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен!
Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом.
Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника.
Кстати, подумай, у каких углов косинус равен ( displaystyle -1)? А у каких ( displaystyle -1) равен синус?
Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!).
Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой.
Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей.
Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать:
Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус.
Углы больше 360 градусов
А как быть с углами, большими чем ( displaystyle 360) градусов?
Возьму я, скажем, угол в ( displaystyle 30) градусов (( displaystyle frac{pi }{6}) радиан) и пойду от него против часовой стрелки…
На рисунке я нарисовал спираль, но ты-то понимаешь, что на самом деле у нас нет никакой спирали: у нас есть только окружность.
Так куда же мы попадем, если стартуем от определенного угла и пройдем полностью весь круг (( displaystyle 360) градусов или ( displaystyle 2pi ) радиан)?
Куда мы придем? А придем мы в тот же самый угол!
Это же, конечно, справедливо и для любого другого угла:
Взяв произвольный угол ( displaystyle alpha ) и пройдя полностью всю окружность, мы вернемся в тот же самый угол ( displaystyle alpha ).
Что же нам это даст? А вот что: если ( displaystyle sin alpha =y,~cos alpha =x), то
( displaystyle sin left( alpha +2pi k right)=y), ( displaystyle cos left( alpha +2pi k right)=x), откуда окончательно получим:
( displaystyle sin left( alpha +2pi k right)=sinalpha )
( displaystyle cos left( alpha +2pi k right)=cosalpha )
Для любого целого ( displaystyle k). Это значит, что синус и косинус являются периодическими функциями с периодом ( displaystyle 2pi ).
Таким образом, нет никакой проблемы в том, чтобы найти знак теперь уже произвольного угла: нам достаточно отбросить все «целые круги», которые умещаются в нашем угле и выяснить, в какой четверти лежит оставшийся угол.
Например, найти знак:
- ( displaystyle text{sin}1000{}^circ ),
- ( displaystyle text{cos} 605{}^circ ),
- ( displaystyle text{cos}frac{16pi }{7}),
- ( displaystyle text{sin}frac{19pi }{4}).
Проверяем:
Отрицательные углы
Отрицательные углы в тригонометрии откладываются на тригонометрическом круге вниз от начала, по направлению движения часовой стрелки:
Давай вспомним, как мы до этого откладывали углы на тригонометрической окружности.
Мы шли от положительного направления оси ( displaystyle Ox) против часовой стрелки:
Тогда на нашем рисунке построен угол, равный ( displaystyle 180+45=225{}^circ ). Аналогичным образом мы строили все углы.
Однако ничего нам не запрещает идти от положительного направления оси ( displaystyle Ox) по часовой стрелке.
Мы будем тоже получать различные углы, но они будут уже отрицательными:
А следующей картинке изображено два угла, равные по абсолютной величине (если не знаешь, что это такое, читай здесь про «Модуль числа»), но противоположные по знаку:
В целом правило можно сформулировать вот так:
- Идем против часовой стрелки – получаем положительные углы
- Идем по часовой стрелке – получаем отрицательные углы
Схематично правило изображено вот на этом рисунке:
Ты мог бы задать мне вполне резонный вопрос: ну углы нам нужны для того, чтобы измерять у них значения синуса, косинуса, тангенса и котангенса.
Так есть ли разница, когда у нас угол положительный, а когда – отрицательный? Я отвечу тебе: как правило есть.
Однако ты всегда можешь свести вычисление тригонометрической функции от отрицательного угла к вычислению функции в угле положительном.
Посмотри на следующую картинку:
Я построил два угла, они равны по абсолютному значению, но имеют противоположный знак. Отметим для каждого из углов его синус и косинус на осях.
Что мы с тобой видим? А вот что:
Синусы у углов ( displaystyle alpha ) и ( displaystyle -alpha ) противоположны по знаку!
Тогда если ( displaystyle text{sin} text{ }!!alpha!!text{ }=text{y}),
то ( displaystyle sin left( -text{ }!!alpha!!text{ } right)=-text{y})
( displaystyle sin left( -text{ }!!alpha!!text{ } right)=-text{sin} text{ }!!alpha!!text{ }).
Косинусы у углов ( displaystyle alpha ) и ( displaystyle -alpha ) совпадают!
Тогда если ( displaystyle text{cos} text{ }!!alpha!!text{ }=text{x}),
то и ( displaystyle cos left( -text{ }!!alpha!!text{ } right)=text{x})
( displaystyle cos left( -text{ }!!alpha!!text{ } right)=text{cos} text{ }!!alpha!!text{ })
Так как ( displaystyle text{tg}left( -text{ }!!alpha!!text{ } right)=frac{text{sin}left( -text{ }!!alpha!!text{ } right)}{text{cos}left( -text{ }!!alpha!!text{ } right)}=frac{-text{sin}left( text{ }!!alpha!!text{ } right)}{text{cos}left( text{ }!!alpha!!text{ } right)}), то:
( displaystyle text{tg}left( -text{ }!!alpha!!text{ } right)=-text{tg }!!alpha!!text{ })
Так как ( displaystyle text{ctg}left( -text{ }!!alpha!!text{ } right)=frac{text{cos}left( -text{ }!!alpha!!text{ } right)}{text{sin}left( -text{ }!!alpha!!text{ } right)}=frac{text{cos}left( text{ }!!alpha!!text{ } right)}{-text{sin}left( text{ }!!alpha!!text{ } right)}), то:
( displaystyle text{ctg}left( -text{ }!!alpha!!text{ } right)=-text{ctg} text{ }!!alpha!!text{ })
Таким образом, мы всегда можем избавиться от отрицательного знака внутри любой тригонометрической функции: либо просто уничтожив его, как у косинуса, либо поставив его перед функцией, как у синуса, тангенса и котангенса.
Кстати, вспомни-ка, как называется функция ( displaystyle f(x)), у которой для любого допустимого ( displaystyle x) выполняется:( displaystyle f(-x)=-f(x))?
Такая функция называется нечетной.
А если же для любого допустимого ( displaystyle x) выполняется: ( displaystyle f(-x)=f(x))? То в таком случае функция называется четной.
Таким образом, мы с тобой только что показали, что:
Синус, тангенс и котангенс – нечетные функции, а косинус – четная.
Таким образом, как ты понимаешь, нет никакой разницы, ищем ли мы синус от положительного угла или отрицательного: справиться с минусом очень просто. Так что нам не нужны таблицы отдельно для отрицательных углов.
С другой стороны, согласись, было бы очень удобно зная только тригонометрические функции углов первой четверти, уметь вычислять аналогичные функции и для остальных четвертей.
Можно ли это сделать? Конечно, можно!
У тебя есть по крайней мере 2 пути: первый – строить треугольник и применять теорему Пифагора (так мы с тобой и отыскали значения тригонометрических функций для основных углов первой четверти)
Второй – запомнив значения функций для углов в первой четверти и некое несложное правило, уметь вычислять тригонометрические функции для всех остальных четвертей.
Второй способ избавит тебя от долгой возни с треугольниками и с Пифагором, поэтому мне он видится более перспективным:
Итак, данный способ (или правило) называется формулами приведения.
Формулы приведения
Грубо говоря, эти формулы помогут тебе не запоминать вот такую таблицу (она между прочим содержит 98 чисел!):
…если ты помнишь вот эту (всего на 20 чисел):
То есть ты сможешь не забивать себе голову совершенно ненужными 78 числами! Пусть, например, нам нужно вычислить ( displaystyle text{sin} 855{}^circ ). Ясно, что в маленькой таблице такого нет. Что же нам делать? А вот что:
Во-первых, нам понадобятся следующие знания:
Синус и косинус имеют период ( displaystyle 2pi ) (( displaystyle 360) градусов)
То есть
( displaystyle sinleft( 2pi k+x right)=sin x)
( displaystyle cosleft( 2pi k+x right)=cos x)
Тангенс (котангенс) имеют период ( displaystyle pi ) (( displaystyle 180) градусов)
( displaystyle tgleft( pi k+x right)=tg x)
( displaystyle ctgleft( pi k+x right)=ctg x)
( displaystyle k) – любое целое число
Синус и тангенс – функции нечетные, а косинус – четная:
( displaystyle sinleft( -x right)=-sin x)
( displaystyle tgleft( -x right)=-tgleft( x right))
( displaystyle cosleft( -x right)=cosleft( x right))
Первое утверждение мы уже доказали с тобой, а справедливость второго установили совсем недавно.
Непосредственно правило приведения выглядит вот так:
Если мы вычисляем значение тригонометрической функции от отрицательного угла – делаем его положительным при помощи группы формул о четности.
Например:
( displaystyle sinleft( -855{}^circ right)=-sin855{}^circ),
( displaystyle cosleft( -855{}^circ right)=cos855{}^circ).
Отбрасываем для синуса и косинуса его периоды: ( displaystyle 2pi k) (по ( displaystyle 360) градусов), а для тангенса – ( displaystyle pi k) (( displaystyle 180) градусов).
Например:
( displaystyle sin 855{}^circ =sinleft( 2cdot 360{}^circ +135{}^circ right)=sin 135{}^circ )( displaystyle tg 225{}^circ =tgleft( 180{}^circ +45{}^circ right)=tg 45{}^circ )
Если оставшийся «уголок» меньше ( displaystyle 90) градусов, то задача решена: ищем его в «малой таблице».
Иначе ищем, в какой четверти лежит наш угол ( displaystyle alpha ): это будет 2, 3 или 4 четверть. Смотрим, какой знак имеет искомая функция в четверти. Запомнили этот знак!!!
Представляем угол ( displaystyle alpha )в одной из следующих форм:
- ( displaystyle alpha =90+beta ) (если во второй четверти)
- ( displaystyle alpha =180-beta ) (если во второй четверти)
- ( displaystyle alpha =180+beta ) (если в третьей четверти)
- ( displaystyle alpha =270-beta ) (если в третьей четверти)
- ( displaystyle alpha =270+beta ) (если в четвертой четверти)
- ( displaystyle alpha =360-beta ) (если в четвертой четверти)
…так, чтобы оставшийся угол ( displaystyle beta ) был больше нуля и меньше ( displaystyle 90) градусов.
Например:
( displaystyle 135{}^circ =180{}^circ -45{}^circ )
( displaystyle 135{}^circ =90{}^circ +45{}^circ )
( displaystyle 315{}^circ =270{}^circ+45{}^circ )
( displaystyle 240{}^circ =180{}^circ +60{}^circ )
( displaystyle 240{}^circ =270{}^circ -30{}^circ )…
В принципе не важно, в какой из двух альтернативных форм для каждой четверти ты представишь угол. На конечном результате это не скажется.
Теперь смотрим, что у нас получилось: если ты выбрал запись через ( displaystyle 180) или ( displaystyle 360) градусов плюс минус что-либо, то знак функции меняться не будет: ты просто убираешь ( displaystyle 180) или ( displaystyle 360) и записываешь синус, косинус или тангенс оставшегося угла.
Если же ты выбрал запись через ( displaystyle 90) или ( displaystyle 270) градусов, то синус меняем на косинус, косинус на синус, тангенс на котангенс, котангенс – на тангенс.
Ставим перед получившимся выражением знак, который мы запомнили.
В статье мы рассмотрим, как найти значения:
(cosfrac{π}{6}), (sin(-frac{7π}{3})), (cosfrac{3π}{4}), (sin(-frac{27π}{2}))
и других тригонометрических выражений без тригонометрической таблицы.
Для начала внимательно прочтите статью о числовой окружности. Вы должны научиться находить точки на окружности в числах с Пи.
Уже умеете? Тогда два ключевых утверждения:
Например, пусть нам нужно найти синус и косинус числа (frac{π}{6}). Обозначим на числовой окружности точку со значением (frac{π}{6}).
Если построить все точно и крупно, то можно убедиться, что абсцисса этой точки будет равна (0,866…) , что соответствует числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Значит, что (cos(frac{π}{6}) = frac{sqrt{3}}{2}), а (sin(frac{π}{6}) =frac{1}{2}).
Аналогично и для любой другой точки: значение абсциссы совпадает со значением косинуса, а ординаты – синуса. Поэтому:
В тригонометрии ось абсцисс часто называют «ось косинусов», а ординат – «ось синусов».
И обычно на них не наносят значения в десятичных ((0,1); (0,2); (0,3) и т.д.), а сразу отмечают стандартные значения для синуса и косинуса: (frac{1}{2} =0,5); (frac{sqrt{2}}{2} ≈0,707); (frac{sqrt{3}}{2}≈0,866), причем, как со знаком плюс, так и минус. Почему стандартные значения синуса и косинуса именно (frac{1}{2}),(frac{sqrt{2}}{2}) и (frac{sqrt{3}}{2}) вы можете узнать из этого видео.
Как находить значения синуса и косинуса без таблицы, а только с помощью круга?
Алгоритм прост:
- Начертите круг и оси косинусов и синусов.
- Отметьте на круге число, синус и косинус которого надо найти. Если с этим возникают проблемы, прочитайте здесь о том, как расставлять числа на числовой окружности.
- Найдите координаты точки, используя картинку ниже.

Пример. Найдите синус и косинус для числа (-frac{7π}{6}).
Решение:(-frac{7π}{6}=-frac{6π}{6}-frac{π}{6}=-π-frac{π}{6}) , то есть, чтобы отметить на окружности точку (-frac{7π}{6}) сначала находим число (-π) и от него в отрицательную сторону откладываем дугу длиной (frac{π}{6}).

Отмечаем число, синус и косинус которого надо найти:

Получается, что (sin(-frac{7π}{6})=frac{1}{2}), (cos(-frac{7π}{6})=-frac{sqrt{3}}{2}).
Пример. Вычислите (sinfrac{5π}{2}) и (cosfrac{5π}{2}).
Решение: (frac{5π}{2}=frac{4π+π}{2}=frac{4π}{2}+frac{π}{2}=2π+frac{π}{2}).

Точка (frac{5π}{2}) совпадает с (1) на оси синусов, значит (sinfrac{5π}{2}=1). А если провести перпендикуляр из точки (frac{5π}{2}) до оси косинусов, то можно убедиться, что он попадет в (0). Поэтому (cosfrac{5π}{2}=0).

И тут некоторые из вас подумали: «с кругом, на котором подписаны числа, каждый дурак сможет посчитать, а что делать, когда его под рукой нет? Что делать на ЕГЭ?» Ответ прост – нарисуйте круг сами! Для этого вам будет нужно понять логику расположения чисел на осях (подробнее об этом читайте в статье «Как запомнить тригонометрический круг»).
Пример. Найдите а) (sinfrac{3π}{2}), б) (cosfrac{3π}{4}), в) (sin(-frac{π}{3})) .
Решение: а) Чертим круг, оси и отмечаем число (frac{3π}{2}). Обращаем внимание на ось синусов и понимаем, что точка совпала с (-1), получается (sinfrac{3π}{2}=-1).
б) (frac{3π}{4}=frac{4π}{4}-frac{π}{4}=π-frac{π}{4}) — отмечаем число на круге. Проводим перпендикуляр до оси косинусов и вспоминаем, что точки со знаменателем (4) находятся посередине. Мы еще попали и в отрицательную часть оси косинусов, получается (cosfrac{3π}{4}=-frac{sqrt{2}}{2}).
в) (-frac{π}{3}) – отмечаем число на круге. Видим, что перпендикуляр к оси синусов попал в точку близкую к (-1), значит (sin(-frac{π}{3})=-frac{sqrt{3}}{2}).

Как видите не обязательно рисовать, очень красивую или очень большую окружность — вы можете определить нужное вам значение, быстро набросав круг. И ничего не надо учить!
Если вы хотите еще примеров с вычислением синусов и косинусов без тригонометрической таблицы, то прочтите эту статью.
Пример (ЕГЭ). Найдите значение выражения (frac{8}{sin(-frac{27π}{4}) cos(frac{31π}{4})}) .
Решение. (-frac{27π}{4}=-frac{28π}{4}+frac{π}{4}=-7π+frac{π}{4}).
(frac{31π}{4}=frac{32π}{4}-frac{π}{4}=8π-frac{π}{4}).

(sin(-frac{27π}{4})=-frac{sqrt{2}}{2}), (cos(frac{31π}{4})=frac{sqrt{2}}{2}).
(frac{8}{sin(-frac{27π}{4}) cos(frac{31π}{4})})(=) (frac{ 8}{-frac{sqrt{2}}{2}cdotfrac{sqrt{2}}{2}})(=-8:frac{2}{4}=-8cdotfrac{2}{1}=-16).
Ответ: (-16).
Смотрите также:
Как найти синус и косинус углов в градусах без тригонометрической таблицы?
Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
-
-
- Перевод градусов в радианы и наоборот. Полный круг содержит
градусов, или
радиан.
- Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси
, а значение синуса — на оси
.
- И синус, и косинус принимают значения от
до
.
- Значение тангенса угла
тоже легко найти — поделив
на
. А чтобы найти котангенс — наоборот, косинус делим на синус.
- Знаки синуса, косинуса, тангенса и котангенса.
- Синус — функция нечётная, косинус — чётная.
- Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен
.
- Перевод градусов в радианы и наоборот. Полный круг содержит
-
А теперь подробно о тригонометрическом круге
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и
, в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами
отвечает углу в
, точка с координатами
— углу в
. Каждому углу от нуля до
градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу
.
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу
.
Например:
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината
. Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от
до
:
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по
(это косинус угла
) и по
(это синус угла
).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует
радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в
, который отложили от положительного направления оси
по часовой стрелке.
Легко заметить, что
,
.
Углы могут быть и больше градусов. Например, угол
— это два полных оборота по часовой стрелке и еще
. Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по
и по
, значения синуса и косинуса повторяются через
. То есть:
,
,
где — целое число.
То же самое можно записать в радианах:
,
.
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения.
По определению:
В результате получим следующую таблицу.
| 0 | |||||||||
| 0 | не существует | 0 | |||||||
| не существует | 0 | не существует |
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Тригонометрический круг: вся тригонометрия на одном рисунке» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023