Ответ:
sinACB=0,6
Объяснение:
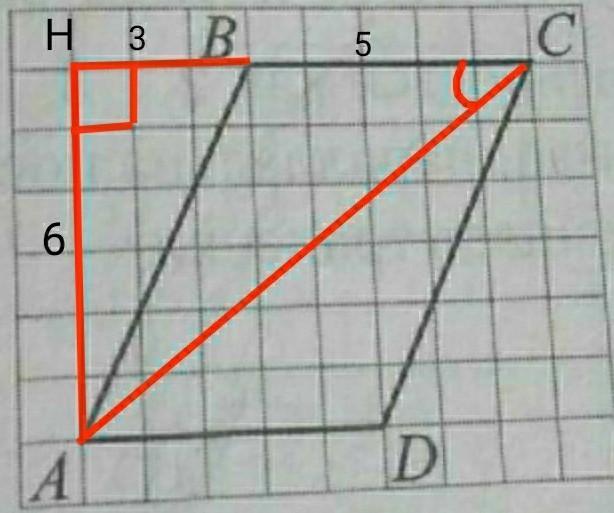
Проведём перпендикуляр АН на продолжение стороны ВС. Получаем прямоугольный треугольник АСН с катетами АН и СН и гипотенузой АС. СН=СВ+ВН=5+3=8.
Найдём. АС по теореме Пифагора:
АС²=АН²+СН²=6²+8²=36+64=100
АС=√100=10.
Синус угла – это отношение противолежащего от угла катета к гипотенузе, поэтому:
sinACB=AH/AC=6/10=0,6
Задания
Версия для печати и копирования в MS Word
Тип 18 № 311366
i
На рисунке с размером клетки 1×1 изображен параллелограмм ABCD. Используя рисунок, найдите
Спрятать решение
Решение.
Синус угла в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе. Треугольник BDC — прямоугольный, поэтому
Вычислим по теореме Пифагора длину гипотенузы CD:
Тогда
Ответ: 0,6.
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.5)
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
Помощь
Ответ:
sinACB=0,6
Объяснение:
Проведём перпендикуляр АН на продолжение стороны ВС. Получаем прямоугольный треугольник АСН с катетами АН и СН и гипотенузой АС. СН=СВ+ВН=5+3=8.
Найдём. АС по теореме Пифагора:
АС²=АН²+СН²=6²+8²=36+64=100
АС=√100=10.
Синус угла – это отношение противолежащего от угла катета к гипотенузе, поэтому:
sinACB=AH/AC=6/10=0,6
Углы параллелограмма. Здравствуйте! В этой публикации представлена группа заданий с параллелограммами. Требуется вычислить синус (косинус) заданного угла, сторону или высоту. Всё решение сводится к работе с прямоугольным треугольником. То есть вполне достаточно помнить определения тригонометрических функций и уметь применять их на практике. Задачи решаются в одно действие, многие ученики после построения эскиза, наверняка, смогут решить их устно.
Что ещё стоит отметить? Один факт (свойство синуса), который очень пригодится. Это то, что синусы смежных углов равны, подробнее об этом было написано в этой статье. Если озвучить кратко и простыми словами, то синусы углов сумма которых равна 1800 равны. Это видно и по формуле приведения:
*а также по тригонометрической окружности (при построении таких углов).
Как это применяется в задачах ниже? Как известно, сумма соседних углов параллелограмма равна 1800. И если будет дан синус любого из углов, то это означает, что синусы соседних с ним углов имеют такое же значение.
Рассмотрим задачи:
27433.В параллелограмме ABCD высота, опущенная на сторону AB равна 4, AD=8. Найдите синус угла B.
Построим высоту:
Синус угла В равен синусу угла А, так как известно, что синусы смежных углов равны (указанные углы в сумме равны 180 градусам).
В прямоугольном треугольнике ADE:
Ответ: 0,5
27434. В параллелограмме ABCD высота, опущенная на сторону AB, равна 4, sinA=2/3. Найдите AD.
Построим указанную высоту:
В прямоугольном треугольнике ADE:
Ответ: 6
27435. В параллелограмме ABCD sinС=3/7. AD=21. Найдите высоту, опущенную на сторону AB.
Построим параллелограмм:
Угол С равен углу А. Рассмотрим прямоугольный треугольник ADE:
Ответ: 9
27436. В параллелограмме ABCD AB=3, AD=21, sinA=6/7. Найдите большую высоту параллелограмма.
Построим параллелограмм соблюдая соотношения сторон (АВ<AD):
Большей будет высота, которая проведена к меньшей стороне. Рассмотрим прямоугольный треугольник ADE:
Ответ: 18
27438. В параллелограмме ABCD cosA=(√51)/10. Найдите sinB.
Как уже сказано, синусы смежных углов равны. Для того, чтобы найти sinB, достаточно вычислить sinА. Из основного тригонометрического тождества следует, что:
Ответ: 0,7
27437. В параллелограмме ABCD sinA=(√21)/5. Найдите cosB.
*Посмотрите решение внимательно, есть важные нюансы.
Посмотреть решение
Этом всё. Есть ещё много задач с параллелограммами, их тоже рассмотрим, не пропустите. Успеха вам!
С уважением, Александр Крутицких.
Материалы принесли вам пользу? Расскажите о сайте в социальных сетях!
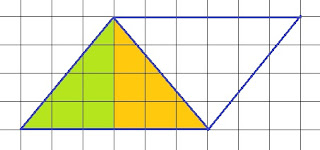
Параллелограмм на клетчатой бумаге
И на ОГЭ в 9 классе, и на ЕГЭ в 11 классе достаточно много заданий на клетчатой бумаге. В этом сообщении мы рассмотрим несколько задач, составленных по одному чертежу.

Задача 1. Найдите площадь этого параллелограмма.
Задача 2. Найдите периметр этого параллелограмма.
Задача 3. Вычислите котангенс острого угла параллелограмма.
Задача 4. Вычислите синус острого угла параллелограмма.
Задача 5. Вычислите косинус острого угла параллелограмма.
Задача 6. Найдите длину меньшей диагонали параллелограмма.
Решение.
Задача 1. Здесь все просто, площадь параллелограмма равна произведению основания на высоту. Основание равно 6, высота 4. Площадь 24.
Задача 2. Чтобы найти периметр этого параллелограмма рассмотрим зеленый прямоугольный треугольник. Его катеты равны 3 и 4, значит гипотенуза равна 5 (по теореме Пифагора). Боковые стороны параллелограмма равны 5. Периметр равен 6+6+5+5=22.
Задача 3. Котангенс острого угла параллелограмма равен отношению прилежащего катета в зеленом треугольнике к противолежащему, то есть 3:4=0,75.
Задача 4. Синус острого угла параллелограмма равен отношению противолежащего катета в зеленом треугольнике к гипотенузе, то есть 4:5=0,8.
Задача 5. Косинус острого угла параллелограмма равен отношению прилежащего катета в зеленом треугольнике к гипотенузе, то есть 3:5=0,6.
Задача 6. Чтобы найдите длину меньшей диагонали параллелограмма, рассмотрим желтый треугольник. Он равен зеленому (катеты у них равны). Значит диагональ равна 5.
Теперь заметим, что данный параллелограмм меньшей диагональю разбивается на два равных равнобедренных треугольника.