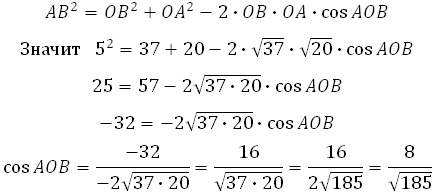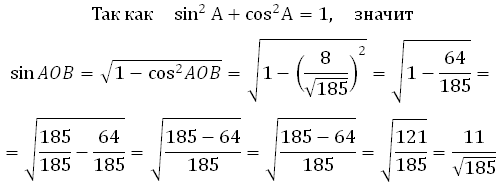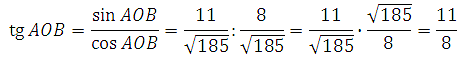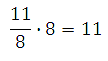Угол на клетчатой бумаге. В этой статье мы с вами рассмотрим задачу, суть которой заключается в том, чтобы найти синус, косинус, тангенс или котангенс угла, построенного на листе в клетку. Такие задания входят в состав экзамена по математике.
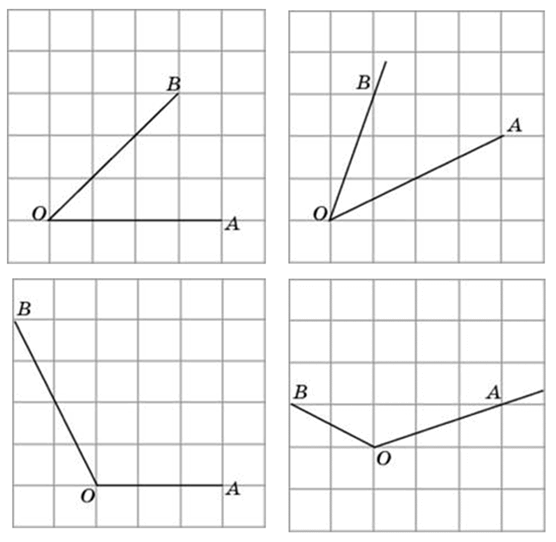
Способы решения существуют разные, их более трёх. Подход изложенный ниже можно было бы назвать универсальным. Если у вас найдутся задачи, которые вы таким способом решить не сможете, пришлите мне их, подберём другой. Углы могут быть построены следующим образом (примеры):
Итак, рассмотрим задание:
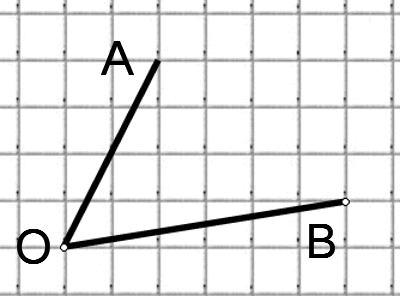
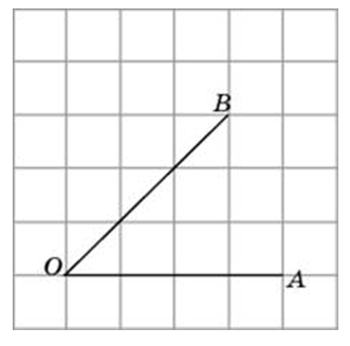
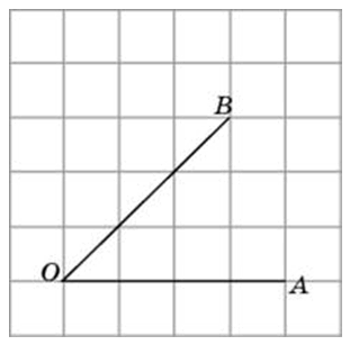
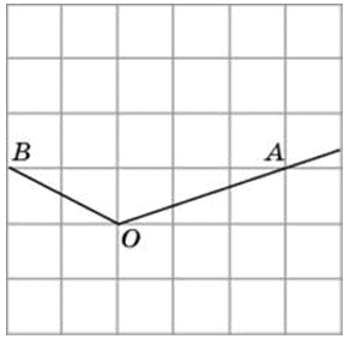
Найдите тангенс угла AOB. В ответе укажите значение тангенса, умноженное на 8.
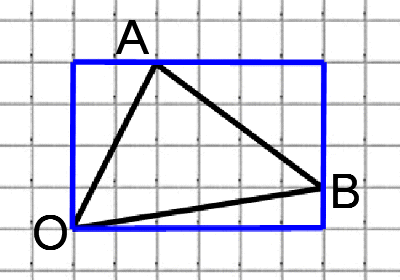
Соединим точки А и В. Получили треугольник АОВ. На сторонах полученного треугольника построим прямоугольные треугольники так, чтобы эти стороны являлись гипотенузами.
Суть подхода такова: находим все стороны треугольника (это можно сделать по теореме Пифагора); далее используя теорему косинусов, мы можем найти косинус угла; зная косинус мы без труда найдём остальные тригонометрические функции (синус, тангенс, котангенс).
АВ это гипотенуза в прямоугольном треугольнике с катетами 4 и 3,
ОВ это гипотенуза в прямоугольном треугольнике с катетами 6 и 1,
OА является гипотенузой в прямоугольном треугольнике с катетами 4 и 2,
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Из основного тригонометрического тождества можем найти sin AOB:
*Обратите внимание, что перед знаком корня у нас «+», так как угол острый (от 0 до 90 градусов). А синус острого угла имеет положительное значение.
Теперь можем найти тангенс:
Умножим результат на 8 и запишем ответ:
Ответ: 11
Ещё раз повторим: как бы не был построен угол, мы всегда можем достроить его до треугольника, найти стороны этого треугольника (используя теорему Пифагора), далее используя теорему косинусов найти косинус угла (заданного в условии). Затем не составит труда, используя основное тригонометрическое тождество, найти синус. Тангенс и котангенс далее не сложно найти по их формулам.
Ниже предложено самостоятельно решить задачи. При их решении на сайте использовались и другие способы (вы решите представленным выше):
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
Найдите тангенс угла AOB.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на половину корня из пяти.
Посмотреть решение
Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на два корня из пяти.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на два корня из двух.
Посмотреть решение
Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на 2 корня из двух.
Посмотреть решение
Найдите тангенс угла AOB.
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
С уважением, Александр Крутицких.
*Делитесь информацией в социальных сетях )
Условие задачи
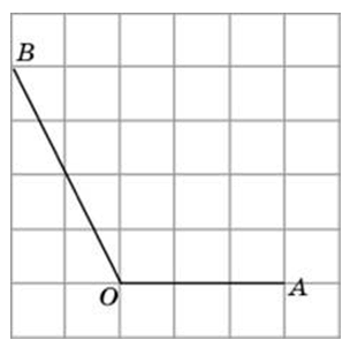
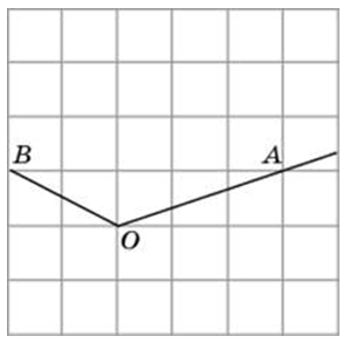
Найдите синус угла АОВ, изображённого на рисунке.
Решение
Опустим из точки В перпендикуляр на прямую ОА. Получим прямоугольный треугольник, катеты которого равны 3 и 4. По теореме Пифагора, его гипотенуза равна 5. Тогда синус угла АОВ равен Мы нашли синус угла как отношение противолежащего катета к гипотенузе.
Ответ:
0,6.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «ОГЭ. Решение. Задание 19, Вариант 2» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Задания
Версия для печати и копирования в MS Word
Тип 29 № 1020
На клетчатой бумаге с размером клетки
изображён угол. Найдите
Спрятать решение
Решение.
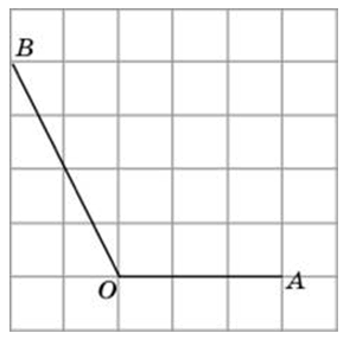
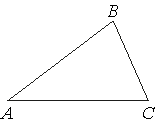
Проведём высоту BH к стороне OA. Получим прямоугольный треугольник с катетами OH = 2 и BH = 4.
Следовательно, гипотенуза этого треугольника, по теореме Пифагора, равна Рассчитаем искомые тригонометрические функции:
Ответ:
Спрятать решение
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
|
Чтобы найти синус угла по клеточкам надо на миллиметровой бумаге циркулем начертить окружность произвольного радиуса предпочтительно кратного десяти. Построить искомый угол, ведя отсчет от верхнего правого квадранта. Из точки пересечения луча угла с окружностью опустить перпендикуляр на ось абсцисс. Посчитать количество клеток пересекаемых этим перпендикуляром и разделить это число на количество клеток в радиусе окружности, это и будет синус угла. Знак взять плюс если луч угла проходит в первом или во втором квадрантах и знак минус для третьего и четвертого . Знаете ответ? |
Вспоминаем, что такое синус, косинус и тангенс в прямоугольном треугольнике.
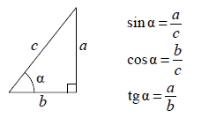
Если на ОГЭ вы от волнения забудете, как находить косинус, синус и тангенс, загляните в справочные материалы на ваших листах с заданиями, там будут подсказки (в разделе геометрии).
В открытом банке заданий ФИПИ есть следующие задачи на эту тему, которые могут вам попасться на реальном экзамене в этом году.
Задания из банка ФИПИ с sin, cos, tg
Найти катет по известному синусу угла и гипотенузе
В треугольнике ABC угол C равен 90°, sinB=4/15, AB=45. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=45*4/15=12Ответ: 12
D8213E
В треугольнике ABC угол C равен 90°, sinB=7/12, AB=48. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=48*7/12=28Ответ: 28
B972FB
В треугольнике ABC угол C равен 90°, sinB=4/11, AB=55. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=55*4/11=20Ответ: 20
E65720
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=51*5/17=15Ответ: 15
D893F0
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=21*3/7=9Ответ: 9
6544F6
В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=18*4/9=8Ответ: 8
F6882F
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=16*5/8=10Ответ: 10
564758
В треугольнике ABC угол C равен 90°, sinB=3/5, AB=10. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=10*3/5=6Ответ: 6
50A4DC
В треугольнике ABC угол C равен 90°, sinB=5/16, AB=80. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=80*5/16=25Ответ: 25
3D5005
В треугольнике ABC угол C равен 90°, sinB=7/20, AB=40. Найдите AC.
Решение:
По определению синуса:
sinB=AC/AB
AC=AB*sinB=40*7/20=14Ответ: 14
14A018
Найти катет по известному косинусу и гипотенузе
В треугольнике ABC угол C равен 90°, cosB=2/5, AB=10. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=10*2/5=4Ответ: 4
1B8713
В треугольнике ABC угол C равен 90°, cosB=5/6, AB=18. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=18*5/6=15Ответ: 15
481278
В треугольнике ABC угол C равен 90°, cosB=4/7, AB=21. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=21*4/7=12Ответ: 12
D4E48F
В треугольнике ABC угол C равен 90°, cosB=3/8, AB=64. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=64*3/8=24Ответ: 24
3F99AC
В треугольнике ABC угол C равен 90°, cosB=7/9, AB=54. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=54*7/9=42Ответ: 42
915280
В треугольнике ABC угол C равен 90°, cosB=9/10, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*9/10=54Ответ: 54
56F660
В треугольнике ABC угол C равен 90°, cosB=5/12, AB=60. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=60*5/12=25Ответ: 25
CA8E29
В треугольнике ABC угол C равен 90°, cosB=9/14, AB=42. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=42*9/14=27Ответ: 27
52D8C1
В треугольнике ABC угол C равен 90°, cosB=11/15, AB=75. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=75*11/15=55Ответ: 55
73E3A7
В треугольнике ABC угол C равен 90°, cosB=13/16, AB=96. Найдите BC.
Решение:
По определению косинуса:
cosB=BC/AB
BC=АВ*cosB=96*13/16=78Ответ: 78
D8738D
Найти катет по известному катету и тангенсу
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=12*3/4=9Ответ: 9
08FD08
В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=18*7/6=21Ответ: 21
1BBB13
В треугольнике ABC угол C равен 90°, tgB=9/7, BC=42. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=42*9/7=54Ответ: 54
14C45C
В треугольнике ABC угол C равен 90°, tgB=8/5, BC=20. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=20*8/5=32Ответ: 32
1DB806
В треугольнике ABC угол C равен 90°, tgB=11/8, BC=24. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=24*11/8=33Ответ: 33
EF04D8
В треугольнике ABC угол C равен 90°, tgB=5/9, BC=27. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=27*5/9=15Ответ: 15
A915AF
В треугольнике ABC угол C равен 90°, tgB=7/12, BC=48. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=48*7/12=28Ответ: 28
48CB65
В треугольнике ABC угол C равен 90°, tgB=4/7, BC=35. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=35*4/7=20Ответ: 20
1EB6B0
В треугольнике ABC угол C равен 90°, tgB=7/4, BC=36. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=36*7/4=63Ответ: 63
93C176
В треугольнике ABC угол C равен 90°, tgB=3/5, BC=30. Найдите AC.
Решение:
По определению тангенса:
tgB=AC/BC
AC=BC*tgB=30*3/5=18Ответ: 18
757BB5
Найти синус по косинусу и наоборот
В решении заданий такого типа используйте основное тригонометрическое тождество
sin2α + cos2α=1
Выражаем то, что нужно найти, и подставляем известные значения.
Синус острого угла А треугольника АВС равен $frac{sqrt{21}}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√21/5)2 = 1 — 21/25 = 1 — 0,84 = 0,16
cosA = 0,4Ответ: 0,4
99B7F9
Синус острого угла А треугольника АВС равен $frac{3sqrt{11}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (3√11/10)2 = 1 — 99/100 = 0,01
cosA = 0,1Ответ: 0,1
E52F99
Синус острого угла А треугольника АВС равен $frac{sqrt{91}}{10}$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√91/10)2 = 1 — 91/100 = 0,09
cosA = 0,3Ответ: 0,3
5F0BC9
Синус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (2√6/5)2 = 1 — 24/25 = 1-0,96 = 0,04
cosA = 0,2Ответ: 0,2
DF0885
Синус острого угла A треугольника ABC равен $frac{3sqrt7}8$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (3√7/8)2 = 1 — 63/64 = 1-0,984375 = 0,015625
cosA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
D56817
Синус острого угла A треугольника ABC равен 4/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (4/5)2 = 1 — 16/25 = 1-0,64 = 0,36
cosA = 0,6Ответ: 0,6
F548B1
Синус острого угла A треугольника ABC равен $frac{sqrt7}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√7/4)2 = 1 — 7/16 = 1-0,4375 = 0,5625
cosA = 0,75Ответ: 0,75
F6FBB5
Синус острого угла A треугольника ABC равен 3/5 . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (3/5)2 = 1 — 9/25 = 1-0,36 = 0,64
cosA = 0,8Ответ: 0,8
4257EE
Синус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√19/10)2 = 1 — 19/100 = 1-0,19 = 0,81
cosA = 0,9Ответ: 0,9
DC7D62
Синус острого угла A треугольника ABC равен $frac{sqrt{15}}4$ . Найдите cosA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
cos2A = 1 — sin2A =1 — (√15/4)2 = 1 — 15/16 = 1-0,9375 = 0,0625
cosA = 0,25Ответ: 0,25
11D7EC
Косинус острого угла A треугольника ABC равен $frac{sqrt{21}}5$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√21/5)2 = 1 — 21/25 = 1-0,84 = 0,16
sinA = 0,4Ответ: 0,4
4BD96F
Косинус острого угла A треугольника ABC равен $frac{3sqrt{11}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (3√11/10)2 = 1 — 99/100 = 1-0,99 = 0,01
sinA = 0,1Ответ: 0,1
EE565F
Косинус острого угла A треугольника ABC равен $frac{sqrt{91}}{10}$ . Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√91/10)2 = 1 — 91/100 = 1-0,91 = 0,09
sinA = 0,3Ответ: 0,3
EE4155
Косинус острого угла A треугольника ABC равен $frac{2sqrt6}5$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (2√6/5)2 = 1 — 24/25 = 1-0,96 = 0,04
sinA = 0,2Ответ: 0,2
2657CA
Косинус острого угла A треугольника ABC равен $frac{3sqrt7}8$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (3√7/8)2 = 1 — 63/64 = 1-0,984375 = 0,015625
sinA = 0,125Ответ: 0,125
Обратите внимание, что корень придется извлекать самостоятельно, поскольку числа 125 (трехзначного) в таблице квадратов на экзамене не будет.
857A3B
Косинус острого угла A треугольника ABC равен 4/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (4/5)2 = 1 — 16/25 = 1-0,64 = 0,36
sinA = 0,6Ответ: 0,6
588CA0
Косинус острого угла A треугольника ABC равен $frac{sqrt7}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√7/4)2 = 1 — 7/16 = 1-0,4375 = 0,5625
sinA = 0,75Ответ: 0,75
5AC6CD
Косинус острого угла A треугольника ABC равен 3/5. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (3/5)2 = 1 — 9/25 = 1-0,36 = 0,64
sinA = 0,8Ответ: 0,8
3B3235
Косинус острого угла A треугольника ABC равен $frac{sqrt{19}}{10}$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√19/10)2 = 1 — 19/100 = 1-0,19 = 0,81
sinA = 0,9Ответ: 0,9
4D93A9
Косинус острого угла A треугольника ABC равен $frac{sqrt{15}}4$. Найдите sinA.
Решение:
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
sin2A = 1 — cos2A =1 — (√15/4)2 = 1 — 15/16 = 1-0,9375 = 0,0625
sinA = 0,25Ответ: 0,25
A426BF
Найти площадь треугольника по двум сторонам и углу между ними
Вспоминаем формулу нахождения площади треугольника по двум сторонам и углу между ними:
S=1/2аb•sinγ, где а и b — стороны треугольника, γ — угол между ними.
Подставляем известные величины и считаем.
Формула так же есть в справочных материалах ОГЭ, на экзамене можете ими воспользоваться.
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*10*1/3=20
Ответ: 20
D8DE10
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=6*12*1/4=18
Ответ: 18
510B5D
В треугольнике ABC известно, что AB=20, BC=7, sin∠ABC=2/5. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=20*7*2/5=56
Ответ: 56
21430B
В треугольнике ABC известно, что AB=15, BC=8, sin∠ABC=5/6. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=15*8*5/6=100
Ответ: 100
770975
В треугольнике ABC известно, что AB=14, BC=5, sin∠ABC=6/7. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=14*5*6/7=60
Ответ: 60
845EFC
В треугольнике ABC известно, что AB=12, BC=20, sin∠ABC=5/8. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*20*5/8=150
Ответ: 150
34F484
В треугольнике ABC известно, что AB=12, BC=15, sin∠ABC=4/9. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*15*4/9=80
Ответ: 80
86F9F5
В треугольнике ABC известно, что AB=16, BC=25, sin∠ABC=3/10. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=16*25*3/10=120
Ответ: 120
6B1EDE
В треугольнике ABC известно, что AB=9, BC=16, sin∠ABC=7/12. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=9*16*7/12=84
Ответ: 84
521C5A
В треугольнике ABC известно, что AB=12, BC=10, sin∠ABC=8/15. Найдите площадь треугольника ABC.
Решение:
S=1/2аb•sinγ=12*10*8/15=64
Ответ: 64
3A3D0B
Найти косинус угла, если известны 3 стороны треугольника

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
а2 = b2 + с2 — 2bс • cosα
Нужно выразить косинус и подставить известные величины.
Эта формула так же будет у вас под рукой на экзамене в справочных материалах ОГЭ.
В треугольнике АВС известно, что AB=8, BC=10, AC=12. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
cosα = (82 +102 — 122) : 2*8*10 = 20/160 = 0,125Ответ: 0,125
40840C
В треугольнике ABC известно, что AB=5, BC=7, AC=9. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+7^2-9^2}{2ast 5ast 7}$ = -7/70 = -0,1
Ответ: -0,1
112015
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{3^2+8^2-7^2}{2ast 3ast 8}$= 24/48 = 0,5
Ответ: 0,5
6E8D8A
В треугольнике ABC известно, что AB=5, BC=10, AC=11. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+10^2-11^2}{2ast 5ast 10}$= 4/100 = 0,04
Ответ: 0,04
844A89
В треугольнике ABC известно, что AB=6, BC=7, AC=8. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+7^2-8^2}{2ast 6ast 7}$= 21/84 = 0,25
Ответ: 0,25
79B29A
В треугольнике ABC известно, что AB=5, BC=6, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{5^2+6^2-4^2}{2ast 5ast 6}$= 45/60 = 0,75
Ответ: 0,75
6557F1
В треугольнике ABC известно, что AB=6, BC=8, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{6^2+8^2-4^2}{2ast 6ast 8}$= 84/96
Ответ: 0,875
B5CF05
В треугольнике ABC известно, что AB=7, BC=8, AC=13. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{7^2+8^2-13^2}{2ast 7ast 8}$= -56/112 = -0,5
Ответ: -0,5
91941D
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{8^2+10^2-14^2}{2ast 8ast 10}$= -32/160 = -0,2
Ответ: -0,2
755B8F
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
Решение:
а2 = b2 + с2 — 2bс • cosα
2bс • cosα = b2 + с2 — а2
$cosalpha=frac{b^2+с^2-а^2}{2bс}$
$cosalpha=frac{2^2+3^2-4^2}{2ast 2ast 3}$= -3/12 = -0,25
Ответ: -0,25
05C64C
Найти синус по двум сторонам
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе. И тот, и другой, известны. Подставляем и считаем.
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/10 = 0,6
Ответ: 0,6
A67245
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 4/5 = 0,8
Ответ: 0,8
46D9DF
В треугольнике ABC угол C равен 90°, AC=7, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 7/25 = 0,28
Ответ: 0,28
6DA700
В треугольнике ABC угол C равен 90°, AC=24, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 24/25 = 0,96
Ответ: 0,96
C7A2A0
В треугольнике ABC угол C равен 90°, AC=6, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 6/20 = 0,3
Ответ: 0,3
ED2D47
В треугольнике ABC угол C равен 90°, AC=11, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 11/20 = 0,55
Ответ: 0,55
F1D3F8
В треугольнике ABC угол C равен 90°, AC=8, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 8/40 = 0,2
Ответ: 0,2
CDC6C7
В треугольнике ABC угол C равен 90°, AC=16, AB=40. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 16/40 = 0,4
Ответ: 0,4
20BC46
В треугольнике ABC угол C равен 90°, AC=9, AB=25. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 9/25 = 0,36
Ответ: 0,36
E2F916
В треугольнике ABC угол C равен 90°, AC=13, AB=20. Найдите sinB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
sinB = АС/АВ = 13/20 = 0,65
Ответ: 0,65
2C2621
Найти косинус по двум сторонам треугольника
Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе. Подставляем известные значения и считаем.
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 8/10 = 0,8
Ответ: 0,8
36727A
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 3/5 = 0,6
Ответ: 0,6
E4988D
В треугольнике ABC угол C равен 90°, BC=14, AB=50. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/50 = 0,28
Ответ: 0,28
B9AA7C
В треугольнике ABC угол C равен 90°, BC=72, AB=75. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 72/75 = 0,96
Ответ: 0,96
6E5515
В треугольнике ABC угол C равен 90°, BC=14, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 14/20 = 0,7
Ответ: 0,7
E812C8
В треугольнике ABC угол C равен 90°, BC=9, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 9/20 = 0,45
Ответ: 0,45
C759C5
В треугольнике ABC угол C равен 90°, BC=30, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 30/40 = 0,75
Ответ: 0,75
8854A8
В треугольнике ABC угол C равен 90°, BC=26, AB=40. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 26/40 = 0,65
Ответ: 0,65
C5CD1E
В треугольнике ABC угол C равен 90°, BC=16, AB=25. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 16/25 = 0,64
Ответ: 0,64
C3A5F2
В треугольнике ABC угол C равен 90°, BC=7, AB=20. Найдите cosB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
cosB = ВС/АВ = 7/20 = 0,35
Ответ: 0,35
D58395
Найти тангенс угла по двум катетам
Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Подставляем значения катетов и считаем.
В треугольнике ABC угол C равен 90°, BC=5, AC=2. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 2/5 = 0,4
Ответ: 0,4
98C7DF
В треугольнике ABC угол C равен 90°, BC=5, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/5 = 0,6
Ответ: 0,6
22FD03
В треугольнике ABC угол C равен 90°, BC=10, AC=7. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 7/10 = 0,7
Ответ: 0,7
C18053
В треугольнике ABC угол C равен 90°, BC=10, AC=8. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 8/10 = 0,8
Ответ: 0,8
33DA26
В треугольнике ABC угол C равен 90°, BC=15, AC=3. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 3/15 = 0,2
Ответ: 0,2
DD620C
В треугольнике ABC угол C равен 90°, BC=9, AC=27. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 27/9 = 3
Ответ: 3
342F0C
В треугольнике ABC угол C равен 90°, BC=5, AC=20. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 20/5 = 4
Ответ: 4
B800B8
В треугольнике ABC угол C равен 90°, BC=3, AC=18. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 18/3 = 6
Ответ: 6
FF498A
В треугольнике ABC угол C равен 90°, BC=4, AC=28. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 28/4 = 7
Ответ: 7
C9E181
В треугольнике ABC угол C равен 90°, BC=7, AC=35. Найдите tgB.
Решение:
∠ C = 90°, значит треугольник прямоугольный.
tgB = АС/ВС = 35/7 = 5
Ответ: 5
0663D4