Как найти синус маленького угла - Avtoru.top - решение различных проблем

§ 4. Малые углы

В принципе можно было бы мерить все углы в радианах. На практике широко используется и градусное измерение углов, хотя с чисто математической точки зрения оно неестественно. При этом для малых углов используются специальные единицы: угловая минута и угловая секунда. Угловая минута — это 1/60 часть градуса; угловая секунда — это 1/60 часть угловой минуты. Если, например, величина угла равна 129 градусам, 34 минутам и 16 секундам, то пишут: 129◦3401600.

Задача 4.1. На какой угол поворачивается за одну секунду:

а) часовая стрелка часов;

б) минутная стрелка часов;

в) секундная стрелка часов?

Решение. Разберем только пункт а). Полный оборот часовая стрелка делает за 12 часов; стало быть, за час она поворачивается на 360/12 = 30◦. Следовательно, за минуту часовая стрелка повернется на угол, в 60 раз меньший, чем за час, то есть на 300;

всвою очередь, за секунду стрелка повернется на угол, в 60 раз меньший, чем за минуту, то есть на 3000. Теперь вы видите, на-

сколько мала угловая секунда: ведь даже угол, в тридцать раз больший (поворот часовой стрелки за секунду времени) мы не

всостоянии заметить.

Представление об угловой минуте дает такой факт: «разрешающая способность» человеческого глаза (при стопроцентном зрении и хорошем освещении) равна примерно одной угловой минуте. Это означает, что две точки, которые видны под углом 10 или меньше, на глаз воспринимаются как одна.

Посмотрим, что можно сказать о синусе, косинусе и тангенсе малых углов. Если на рис. 4.2 угол α мал, то высота BC, дуга BD и отрезок BE, перпендикулярный AB, очень близки. Их длины — это sin α, радианная мера α и tg α. Стало быть, для малых углов синус, тангенс и радианная мера приближенно равны друг другу:

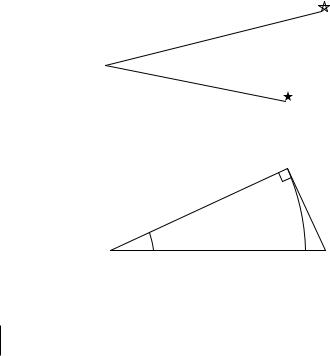
Рис. 4.1. Разрешающая способность.



	Рис. 4.2. Малые углы.

Если α — малый угол, измеренный в радианах, то sin α ≈ α; tg α ≈ α.

Задача 4.2. Запишите приближенные формулы для синуса и тангенса малых углов, считая, что угол измеряется в градусах.

Ответ. sin α◦ ≈ πα/180.

Видно, что формулы сложнее, чем для радианной меры — еще один довод в ее пользу!

Задача 4.3. Под каким углом видно дерево высотой 10 метров с расстояния в 800 метров? Дайте ответ: а) в радианах; б) в угловых минутах.

Задача 4.4. Чему равно расстояние, равное одной минуте дуги земного меридиана? Радиус Земли равен примерно 6370 .

Расстояние, о котором идет речь в этой задаче, примерно равно морской миле (именно так и появилась эта мера длины).

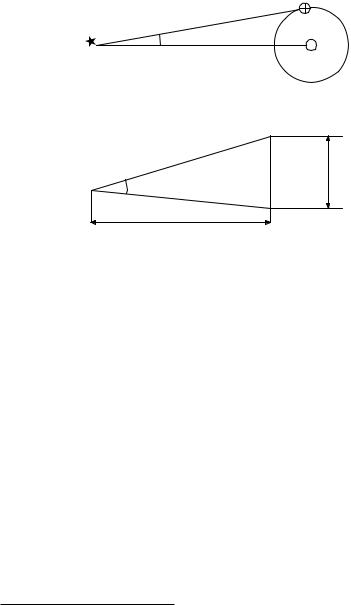
Рис. 4.3. Парсек.

Рис. 4.4. Формула тысячных.

Задача 4.5. В астрономии применяется единица измерения расстояний, называемая парсек. По определению, расстояние в 1 парсек — это расстояние с которого радиус земной орбиты1 виден под углом 100 (рис. 4.3). Сколько километров в одном парсеке? (Радиус земной орбиты равен примерно 150 миллионам километров.)

Задача 4.6. Военные пользуются единицей измерения углов, называемой «тысячная». По определению, тысячная — это 1/3000 развернутого угла. Такое измерение углов военные применяют в следующей формуле для определения расстояния до удаленных предметов: = (/) · 1000. Здесь — расстояние до предмета, — его высота, — угол, под которым он виден, измеренный в тысячных (рис. 4.4). Точна ли эта формула? Почему ей можно пользоваться на практике? Чему равно число π, по мнению военных?

Мы видим, что формулы sin α ≈ α, tg α ≈ α верны с хорошей точностью для малых углов. Посмотрим, что произойдет,

1Астрономы поправили бы нас: не радиус (орбита Земли — не круг, а эллипс), а большая полуось (половина расстояния между наиболее удаленными друг от друга точками орбиты).

если угол не столь мал. Для угла в 30◦ точное значение синуса равно 0,5, а радианная мера равна π/6 ≈ 0,52. Ошибка (или, как еще говорят, погрешность), которую дает формула sin α ≈ α, равна примерно 0,02, что составляет 4% от значения синуса. Можно сказать, что относительная погрешность при таком вычислении (отношение погрешности к значению синуса) составляет 4%. Для углов, меньших 10◦, относительная погрешность формулы sin α ≈ α меньше одного процента. Чем меньше угол α, тем меньше относительная погрешность формулы sin α ≈ α.

Существуют и другие формулы, позволяющие вычислять синусы и тангенсы — и не только малых углов — с хорошей точностью. Например, формула sin α ≈ α − α3/6 (напоминаем, что α измеряется в радианах!) дает относительную погрешность менее 1% уже для всех углов, не превосходящих 50◦. Позднее мы увидим, как оценить погрешность наших формул.

Задача 4.7. Пусть α — острый угол, измеренный в радианах. Докажите неравенство cos α > 1 − α2.


Указание. Воспользуйтесь формулой cos α =	1 − sin2 α, нера-
√		0 < t < 1	).
венством sin α < α и неравенством t > t (для p

Задача 4.8. Для косинусов малых углов в качестве приближенного значения можно брать 1. Докажите, что при величине угла менее 5◦ относительная погрешность этого приближения будет менее 1%.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Синус в треугольнике

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно, синус угла B в треугольнике ABC

равен отношению AC к AB:

Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.

Синус угла. Таблица синусов.

Синус угла через градусы, минуты и секунды

Синус угла через десятичную запись угла

Как найти угол зная синус этого угла

У синуса есть обратная тригонометрическая функция — arcsin(y)=x

Пример sin(30°) = 1/2; arcsin(1/2) = 30°

Определение синуса

Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

Периодичность синуса

Функция y = sin(x) периодична, с периодом 2π

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

На b сокращаем, синусы переносим в знаменатели:

bc sinα = ca sinβ

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

Стороны треугольника, если даны два угла и одна сторона.
Углы треугольника, если даны две стороны и один прилежащий угол.

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° — α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° — α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° — α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

sin120° = sin(180° — 60°) = sin60° = 3/√2;
sin150° = sin(180° — 30°) = sin30° = 1/2;
sin135° = sin(180° — 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° — α)

Так как sin(180° — α) = sinα, то sinγ = sin(180° — α) = sinα

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° — 45° — 15° = 120°

Сторону AC найдем по теореме синусов:

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

источники:

http://calc-best.ru/matematicheskie/trigonometriya/sinus-ugla?n1=3

http://skysmart.ru/articles/mathematic/teorema-sinusov

Источник

Чему равен синус наименьшего угла треугольника в задаче (см)? Как решить?

Новосибирск
[3.2K]

5 лет назад

В прямоугольном треугольнике катеты относятся как 3:4. Чему равен синус наименьшего угла треугольника?

Вячеслав Четвертый
[9.1K]

5 лет назад

Согласно теореме Пифагора, гипотенуза будет кратна 5. А это значит, что синус наименьшего угла будет равен отношению меньшего катета на гипотенузу, то есть, ответ будет 0,6 или три пятые. Можно найти синус и через тангенс, но так будет более сложное решение.

комментировать

в избранное

ссылка

отблагодарить

Знаете ответ?

Источник

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Определение.

Например,

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

$[sin angle A = frac{{BC}}{{AB}}]$

Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно, синус угла B в треугольнике ABC

равен отношению AC к AB:

$[sin angle B = frac{{AC}}{{AB}}]$

Вывод:

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

Например,

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

Тогда

$[sin angle A = frac{{BC}}{{AB}} = frac{3}{5}.]$

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Тогда

$[sin angle A = frac{{BC}}{{AB}} = frac{{21}}{{35}} = frac{3}{5}.]$

Угол A в обоих треугольниках одинаков.

Источник

Свойства тригонометрических функций

Отсюда вытекает много интересных свойств и тригонометрических формул.
Во-первых, надеюсь, все знают, что в прямоугольном треугольнике самая большая сторона – это гипотенуза.
Поэтому из определения синуса и косинуса ((sin(alpha)=frac{a}{c}; quad cos(alpha)=frac{b}{c})) следует, что они всегда меньше единицы, ведь мы катет (меньшую сторону) делим на гипотенузу (большую сторону треугольника). И как мы узнаем позже, синус и косинус всегда больше минус единицы. То есть синус и косинус могут принимать только значения из промежутка:

$$ sin(alpha) in [-1;1];$$
$$ cos(alpha) in [-1;1];$$

Для тангенса и котангенса никаких ограничений нет, они могут принимать абсолютно любые значения.

Теперь выведем несколько формул, без которых нам точно потом не обойтись. Например, можно обратить внимание, что тангенс выражается через деление синуса на косинус, просто расписав их по определению:

$$frac{sin(alpha)}{cos(alpha)}=frac{frac{a}{c}}{frac{b}{c}}=frac{a}{c}*frac{c}{b}=frac{a}{b};$$

А последняя формула есть ни что иное, как определение тангенса:
$$ tg(alpha)=frac{a}{b};$$
Значит
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}.$$

Аналогичные рассуждения можно провести для котангенса:
$$frac{cos(alpha)}{sin(alpha)}=frac{frac{b}{c}}{frac{a}{c}}=frac{b}{c}*frac{c}{a}=frac{b}{a};$$
А котангенс по определению:
$$ctg(alpha)=frac{b}{a};$$
Значит
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}.$$

Кроме этого, легко заметить, что функции тангенса и котангенса взаимно обратны:
$$tg(alpha)*ctg(alpha)=frac{a}{b}*frac{b}{a}=1.$$

А теперь мы подобрались к не самой очевидной тригонометрической формуле, но одной из самых главных во всей тригонометрии. Основное тригонометрическое тождество:

$$sin^2(alpha)+cos^2(alpha)=1. qquad (1)$$

Выводится оно тоже из определений синуса и косинуса с использованием теоремы Пифагора (гипотенуза в прямоугольном треугольнике равна сумме квадратов катетов (c^2=a^2+b^2;)):
$$sin^2(alpha)+cos^2(alpha)=left(frac{a}{c}right)^2+left(frac{b}{c}right)^2=left(frac{a^2}{c^2}right)+left(frac{b^2}{c^2}right)=frac{a^2+b^2}{c^2}=frac{c^2}{c^2}=1.$$
С основным тригонометрическим тождеством вы будете сталкиваться постоянно и в 9-м и в 10-м классах.

И разберем еще две важные формулы:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
Выводится она очень легко, опять же, используя определения тангенса и косинуса. Рекомендую потренироваться и сделать это самим.
$$1+left(frac{a}{b}right)^2=frac{1}{frac{b^2}{c^2}};$$
$$left(frac{b^2}{b^2}right)+left(frac{a^2}{b^2}right)=1*frac{c^2}{b^2};$$
$$frac{b^2+a^2}{b^2}=frac{c^2}{b^2};$$
Используем теорему Пифагора:
$$frac{c^2}{b^2}=frac{c^2}{b^2};$$
Получили верное равенство, значит формула верна.

И вторая аналогичная формула для котангенса:
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)};$$
Вывод один в один, сделайте сами.

Для удобства соберем все формулы вместе.
$$sin^2(alpha)+cos^2(alpha)=1. qquad(1)$$
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}. qquad(2)$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}. qquad(3)$$
$$tg(alpha)*ctg(alpha)=1.qquad(4)$$
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)}. qquad(5)$$
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}. qquad(6)$$

Это далеко не все тригонометрические формулы, их гораздо больше. Но для начала и для 9-го класса этого вполне достаточно.

Зачем же они нужны? Оказывается, эти формулы помогают связать тригонометрические функции между собой. Посмотрите внимательно на первую формулу (1): зная, например, чему равен косинус, можно легко найти синус, и наоборот.

Пример 1
Пусть (cos(alpha) =frac{1}{2}), найдите (sin(alpha)=?)

Берем основное тригонометрическое тождество (формула (1)) и подставляем в него известный по условию задачи (cos(alpha)=frac{1}{2}:)
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(frac{1}{2}right)^2=1;$$
А дальше просто решаем получившееся уравнение относительно синуса:
$$sin^2(alpha)=1-left(frac{1}{2}right)^2;$$
$$sin^2(alpha)=1-frac{1}{4};$$
Приводим к общему знаменателю:

$$sin^2(alpha)=frac{4}{4}-frac{1}{4};$$
$$sin^2(alpha)=frac{3}{4};$$
И здесь внимательно решаем квадратное уравнение:
$$sin(alpha)=pmfrac{sqrt{3}}{2};$$
Обратите внимание на (pm). Синус может быть как положительным, так и отрицательным, так как при подстановке и возведении в квадрат минус сгорает. Значит здесь получается два ответа.

Ответ:(sin(alpha)=pmfrac{sqrt{3}}{2}.)

Аналогично, зная хотя бы одну тригонометрическую функцию, можно найти все остальные, используя тригонометрические формулы. Рассмотрим еще пример:

Пример 2
Пусть (sin(alpha) =frac{1}{3}), найдите (ctg(alpha)=?)

Смотрим на наш список формул и находим такую, в которой есть и синус и котангенс — это формула (6):
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}.$$
Подставляем известный из условия синус (sin(alpha) =frac{1}{3}):
$$1+сtg^2(alpha)=frac{1}{left(frac{1}{3}right)^2}.$$
Перевернем правую часть:
$$1+сtg^2(alpha)=left(frac{3}{1}right)^2.$$
$$1+сtg^2(alpha)=9.$$
Теперь решим уравнение и найдем котангенс:
$$сtg^2(alpha)=8.$$
$$сtg(alpha)=pmsqrt{8}=pmsqrt{4}*sqrt{2}=pm2sqrt{2}.$$

Ответ:(сtg(alpha)=pm2sqrt{2}).

Выглядит пугающе, но учить вам это НЕ НУЖНО! В некоторых школах есть изверги, которые заставляют учить такую таблицу, но в этом совершенно нет необходимости. В дальнейшем мы научимся сами выводить все значения тригонометрических функций только из маленькой таблицы.

Обратите внимание, что синус некоторого угла в треугольнике всегда положителен, неважно, тупой или острый угол. А вот косинус, тангенс и котангенс в треугольнике положительны только от острых углов и отрицательны от тупых.

Тут может возникнуть вопрос, как может существовать синус, косинус, тангенс или котангенс от тупого угла, большего чем (90^o), если мы давали определение всех тригонометрических функций через прямоугольный треугольник, в котором нет углов больших (90^o). Ну что ж, да тригонометрические функции существуют для любых углов и острых, и тупых, но для самого начала тригонометрии определения через прямоугольный треугольник нам более чем достаточно. Просто запомните выводы, которые мы сделали в предыдущем абзаце.

Рассмотрим пример на тригонометрию по типу схожий с заданиями ОГЭ. Обычно задачи сводятся просто к нахождению тригонометрической функции некоторого угла, нарисованного на рисунке:

Пример 2
По рисунку определить значение (sin(alpha)=?)

По определению синус в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Первым делом достроим наш синий угол (angle{ABC}) до прямоугольного треугольника, для этого опустим из точки (A) высоту (AH) к (BC). Получили прямоугольный треугольник (AHB). Теперь можем воспользоваться определением синуса:
$$sin(alpha)=frac{AH}{AB};$$
По клеточкам на рисунке найдем длину отрезка (AH=15). А гипотенузу (AB) найти по клеточкам не выйдет, так как она идет по диагонали. Но мы можем найти опять по клеточкам второй катет в прямоугольном треугольнике (BH=12) и применить теорему Пифагора:
$$AB^2=AH^2+BH^2;$$
$$AB^2=15^2+12^2=225+144=369;$$
$$AB=sqrt{369}=3sqrt{41};$$
Подставим в формулу для синуса и найдем его:
$$sin(alpha)=frac{AH}{AB}=frac{15}{3sqrt{41}};$$

Ответ: (sin(alpha)= frac{15}{3sqrt{41}}.)

Разберем еще примеры посложнее на нахождение тригонометрических функций друг через друга. Некоторые даже будут из реального ЕГЭ:

Пример 3
Пусть (tg(alpha)=sqrt{3}), найти (cos(alpha)=?), если известно, что (alpha<90^o).
Задание из ЕГЭ по профильной математике.

Условие аналогично условию в примерах №1 и 2, но появилось еще какое-то ограничение на угол (alpha), пока не будем обращать на него внимания, и решаем как обычно. Воспользуемся формулой (5), в ней есть и косинус, и тангенс, как раз одна из функций нам дана, а другую надо найти:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(sqrt{3})^2=frac{1}{cos^2(alpha)};$$
$$1+3=frac{1}{cos^2(alpha)};$$
$$4=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{4};$$
$$cos(alpha)=pmfrac{1}{2}.$$

У нас опять получилось два ответа из-за квадрата. В условии сказано, что задание из первой части ЕГЭ, а значит два ответа быть не может. Для этого нам и дано, что (alpha<90^o). Это означает, что угол (alpha) острый, а значит косинус у острого угла обязательно должен быть положительный.

Ответ: (cos(alpha)=frac{1}{2}.)

Пример 4
Пусть (tg(alpha) =-2), найти (sin(alpha)=?), при (90^o<alpha<180^o).

Опять обратимся к нашим формулам (1-6) и пытаемся найти такую, в которой есть и синус и тангенс. И тут оказывается, что такой формулы нет. Но нам никто не запрещает, зная тангенс и используя формулу (5), найти косинус:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(-2)^2=frac{1}{cos^2(alpha)};$$
$$5=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{5};$$
$$cos^2(alpha)=pmsqrt{frac{1}{5}};$$
Так как согласно условию (alpha>90^o), то значение косинуса должно быть отрицательным:
$$cos(alpha)=-sqrt{frac{1}{5}};$$

А потом, уже зная косинус, по основному тригонометрическому тождеству (1) можно найти требуемый в задаче синус:
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(-sqrt{frac{1}{5}}right)^2=1;$$
$$sin^2(alpha)+frac{1}{5}=1;$$
$$sin^2(alpha)=-frac{1}{5}+1;$$
$$sin^2(alpha)=frac{4}{5};$$
$$sin(alpha)=pmsqrt{frac{4}{5}};$$
Синус у нас положительный и при острых ((alpha<90^o)) и при тупых углах ( (90<alpha<180) ):
$$sin(alpha)=sqrt{frac{4}{5}};$$

Ответ: (sin(alpha)=sqrt{frac{4}{5}}.)

Итак, зная значение хотя бы одной из четырех тригонометрических функций, при помощи формул (1-6) можно найти три оставшихся, именно для этого формулы и нужны.

Зная угол (angle{A}=60^o), мы знаем все тригонометрические функции от этого угла. Смотрите в таблицу (1):
$$sin(60^o)=frac{sqrt{3}}{2};$$
$$cos(60^o)=frac{1}{2};$$
$$tg(60^o)=sqrt{3};$$
$$ctg(60^o)=frac{1}{sqrt{3}};$$
С другой стороны, можно расписать функции по определению через отношение сторон в прямоугольном треугольнике:
$$sin(angle{A})=frac{BC}{AB};$$
$$cos(angle{A})=frac{AC}{AB};$$
$$tg(angle{A})=frac{BC}{AC};$$
$$ctg(angle{A})=frac{AC}{BC};$$

Не пугайтесь, все нам не понадобится. Воспользуемся пока формулами:
$$cos(60^o)=frac{1}{2};$$
$$cos(angle{A}=60^o)=frac{AC}{AB};$$
Нам известны косинус (angle{A}) и сторона (AC), а значит, мы можем найти гипотенузу (AB):
$$frac{1}{2}=frac{5}{AB};$$
$$AB=frac{5}{frac{1}{2}}=5*frac{2}{1}=10;$$
Нашли гипотенузу, теперь найдем последнюю сторону (BC). Для этого нам нужна любая формула с (BC), например:
$$sin(angle{A})=frac{BC}{AB};$$
Синус знаем, (AB) только что нашли — выражаем (BC):
$$BC=AB*sin(60^o)=10*frac{sqrt{3}}{2}=5*sqrt{3}.$$

Ответ: (AB=10;) (BC=5*sqrt{3}.)

Подведем итоги. Зная любую сторону в прямоугольном треугольнике и хотя бы один из острых углов, можно найти все остальные стороны при помощи тригонометрии.

Рассмотрим задачу посложнее.

Пример 6
Дан прямоугольный треугольник (bigtriangleup{ABC}), в котором угол (angle{C}=90^o), угол (tg(angle{A})=frac{1}{5}), сторона (AB=13). В треугольнике из прямого угла (angle{C}) проведена высота (CH). Найти (AH).

Первым делом обратите внимание на один очень важный факт. Если провести высоту в прямоугольном треугольнике из прямого угла, то она поделит треугольник еще на два прямоугольных. В нашем случае (bigtriangleup{ACH}) и (bigtriangleup{CHB}) тоже будут прямоугольными. А значит в них выполняются все соотношения для тригонометрических функций.
Например, в (bigtriangleup{ACH}) для угла (angle{A}) противолежащим катетом будет (CH), а прилежащим — сторона (AH), гипотенуза будет соответственно (AC). А значит можно записать формулы, следующие из определения тригонометрических функций:

$$sin(angle{A})=frac{CH}{AC};$$
$$cos(angle{A})=frac{AH}{AC};$$
$$tg(angle{A})=frac{CH}{AH};$$
$$ctg(angle{A})=frac{AH}{CH};$$

Аналогичные соотношения можно записать и для (bigtriangleup{CHB}) и (bigtriangleup{ABC}). Не буду нагромождать, запишите эти соотношения сами в качестве тренировки.

Следующий важный момент, на который следует обратить внимание — это углы в получившихся треугольниках. Обозначим угол (angle{CAB}=alpha). Тогда, так как (angle{CHA}=90^o), можно выразить угол:
$$angle{ACH}=180-angle{CAB}-angle{CHA}=180-alpha-90=90-alpha;$$
Напомню, что треугольник (bigtriangleup{ABC}) прямоугольный с прямым углом (angle{ACB}=90^o).
Значит
$$angle{HCB}=angle{ACB}-angle{ACH}=90-(90-alpha)=alpha=angle{CAB};$$

Важный факт: (angle{HCB}=angle{CAB})! А равенство этих углов само собой означает и равенство всех тригонометрических функций. То есть, например, (sin(angle{HCB})=sin(angle{ACB})). Точно так же у них равны и косинусы, и тангенсы, и даже котангенсы!

Аналогичные рассуждения можно провести для углов (angle{ACH}=angle{CBA}).
Запомните это!

А теперь приступим непосредственно к решению задачи. Нам известна гипотенуза (AB) и (tg(alpha)). По определению тангенса в (bigtriangleup{ABC}):
$$tg(angle{A})=frac{CB}{AC};$$
Либо из (bigtriangleup{ACH}):
$$tg(angle{A})=frac{CH}{AH};$$

В этих формулах есть проблема: нет известной нам стороны, гипотенузы (AB). А значит, у нас две неизвестные, и решить мы не можем.

Но зная тангенс, мы легко можем найти косинус по формуле:
$$1+tg(alpha)^2=frac{1}{cos^2(alpha)};$$
$$1+left(frac{1}{5}right)^2=frac{1}{cos^2(alpha)};$$
$$1+frac{1}{25}=frac{1}{cos^2(alpha)};$$
$$frac{26}{25}=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{frac{26}{25}}=1*frac{25}{26}=frac{25}{26};$$
$$cos(alpha)=pmsqrt{frac{25}{26}}=pmfrac{5}{sqrt{26}};$$
Так как (anglealpha) это острый угол из прямоугольного треугольника, то его косинус точно будет положительным:
$$cos(alpha)=frac{5}{sqrt{26}}.$$
Не самый приятный косинус, но что делать, будем решать так, как есть.

С другой стороны, из (bigtriangleup{ABC}):
$$cos(alpha)=frac{AC}{AB};$$
Подставим известное (AB):
$$frac{5}{sqrt{26}}=frac{AC}{13};$$
$$AC=13*frac{5}{sqrt{26}}=frac{13*5}{sqrt{26}};$$
Либо косинус еще можно расписать в (bigtriangleup{ACH}):
$$cos(alpha)=frac{AH}{AC}=frac{5}{sqrt{26}};$$
Подставим найденное (AC):
$$frac{AH}{frac{13*5}{sqrt{26}}}=frac{5}{sqrt{26}};$$
$$AH=frac{5}{sqrt{26}}*frac{13*5}{sqrt{26}}=frac{5*13*5}{26}=frac{25}{2}=12,5.$$

Ответ: (AH=12,5.)

Источник

§ 4. Малые углы

Синус в треугольнике

Синус угла. Таблица синусов.

Синус угла через градусы, минуты и секунды

Синус угла через десятичную запись угла

Как найти угол зная синус этого угла

Определение синуса

Периодичность синуса

Теорема синусов

Доказательство теоремы синусов

Доказательство следствия из теоремы синусов

Теорема о вписанном в окружность угле

Примеры решения задач

Запоминаем

Чему равен синус наименьшего угла треугольника в задаче (см)? Как решить?

Свойства тригонометрических функций

Не пропустите также: