В статье мы рассмотрим, как найти значения:
(cosfrac{π}{6}), (sin(-frac{7π}{3})), (cosfrac{3π}{4}), (sin(-frac{27π}{2}))
и других тригонометрических выражений без тригонометрической таблицы.
Для начала внимательно прочтите статью о числовой окружности. Вы должны научиться находить точки на окружности в числах с Пи.
Уже умеете? Тогда два ключевых утверждения:
Например, пусть нам нужно найти синус и косинус числа (frac{π}{6}). Обозначим на числовой окружности точку со значением (frac{π}{6}).
Если построить все точно и крупно, то можно убедиться, что абсцисса этой точки будет равна (0,866…) , что соответствует числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Значит, что (cos(frac{π}{6}) = frac{sqrt{3}}{2}), а (sin(frac{π}{6}) =frac{1}{2}).
Аналогично и для любой другой точки: значение абсциссы совпадает со значением косинуса, а ординаты – синуса. Поэтому:
В тригонометрии ось абсцисс часто называют «ось косинусов», а ординат – «ось синусов».
И обычно на них не наносят значения в десятичных ((0,1); (0,2); (0,3) и т.д.), а сразу отмечают стандартные значения для синуса и косинуса: (frac{1}{2} =0,5); (frac{sqrt{2}}{2} ≈0,707); (frac{sqrt{3}}{2}≈0,866), причем, как со знаком плюс, так и минус. Почему стандартные значения синуса и косинуса именно (frac{1}{2}),(frac{sqrt{2}}{2}) и (frac{sqrt{3}}{2}) вы можете узнать из этого видео.
Как находить значения синуса и косинуса без таблицы, а только с помощью круга?
Алгоритм прост:
- Начертите круг и оси косинусов и синусов.
- Отметьте на круге число, синус и косинус которого надо найти. Если с этим возникают проблемы, прочитайте здесь о том, как расставлять числа на числовой окружности.
- Найдите координаты точки, используя картинку ниже.

Пример. Найдите синус и косинус для числа (-frac{7π}{6}).
Решение:(-frac{7π}{6}=-frac{6π}{6}-frac{π}{6}=-π-frac{π}{6}) , то есть, чтобы отметить на окружности точку (-frac{7π}{6}) сначала находим число (-π) и от него в отрицательную сторону откладываем дугу длиной (frac{π}{6}).

Отмечаем число, синус и косинус которого надо найти:

Получается, что (sin(-frac{7π}{6})=frac{1}{2}), (cos(-frac{7π}{6})=-frac{sqrt{3}}{2}).
Пример. Вычислите (sinfrac{5π}{2}) и (cosfrac{5π}{2}).
Решение: (frac{5π}{2}=frac{4π+π}{2}=frac{4π}{2}+frac{π}{2}=2π+frac{π}{2}).

Точка (frac{5π}{2}) совпадает с (1) на оси синусов, значит (sinfrac{5π}{2}=1). А если провести перпендикуляр из точки (frac{5π}{2}) до оси косинусов, то можно убедиться, что он попадет в (0). Поэтому (cosfrac{5π}{2}=0).

И тут некоторые из вас подумали: «с кругом, на котором подписаны числа, каждый дурак сможет посчитать, а что делать, когда его под рукой нет? Что делать на ЕГЭ?» Ответ прост – нарисуйте круг сами! Для этого вам будет нужно понять логику расположения чисел на осях (подробнее об этом читайте в статье «Как запомнить тригонометрический круг»).
Пример. Найдите а) (sinfrac{3π}{2}), б) (cosfrac{3π}{4}), в) (sin(-frac{π}{3})) .
Решение: а) Чертим круг, оси и отмечаем число (frac{3π}{2}). Обращаем внимание на ось синусов и понимаем, что точка совпала с (-1), получается (sinfrac{3π}{2}=-1).
б) (frac{3π}{4}=frac{4π}{4}-frac{π}{4}=π-frac{π}{4}) — отмечаем число на круге. Проводим перпендикуляр до оси косинусов и вспоминаем, что точки со знаменателем (4) находятся посередине. Мы еще попали и в отрицательную часть оси косинусов, получается (cosfrac{3π}{4}=-frac{sqrt{2}}{2}).
в) (-frac{π}{3}) – отмечаем число на круге. Видим, что перпендикуляр к оси синусов попал в точку близкую к (-1), значит (sin(-frac{π}{3})=-frac{sqrt{3}}{2}).

Как видите не обязательно рисовать, очень красивую или очень большую окружность — вы можете определить нужное вам значение, быстро набросав круг. И ничего не надо учить!
Если вы хотите еще примеров с вычислением синусов и косинусов без тригонометрической таблицы, то прочтите эту статью.
Пример (ЕГЭ). Найдите значение выражения (frac{8}{sin(-frac{27π}{4}) cos(frac{31π}{4})}) .
Решение. (-frac{27π}{4}=-frac{28π}{4}+frac{π}{4}=-7π+frac{π}{4}).
(frac{31π}{4}=frac{32π}{4}-frac{π}{4}=8π-frac{π}{4}).

(sin(-frac{27π}{4})=-frac{sqrt{2}}{2}), (cos(frac{31π}{4})=frac{sqrt{2}}{2}).
(frac{8}{sin(-frac{27π}{4}) cos(frac{31π}{4})})(=) (frac{ 8}{-frac{sqrt{2}}{2}cdotfrac{sqrt{2}}{2}})(=-8:frac{2}{4}=-8cdotfrac{2}{1}=-16).
Ответ: (-16).
Смотрите также:
Как найти синус и косинус углов в градусах без тригонометрической таблицы?
Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
Значение выражения sin (п / 6) можно вычислить несколькими способами.
Способ №1.
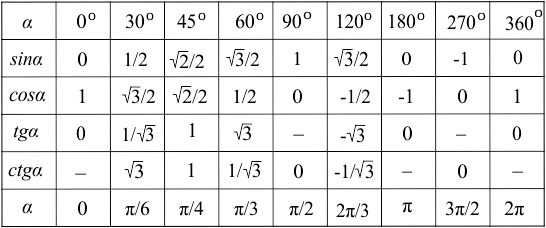
Самым распространенным способом (как в школе, так и вузе) из всех существующих является использование таблицы значений тригонометрических функций от основных значений аргументов.
Удобно использовать таблицу, в которой значение аргумента представлено и в радианах, и в градусах (легче можно сориентироваться). Также по градусам легче понять размер угла. Но в задачах чаще всего встречаются аргументы, представленные в радианах.
По таблице определим значение синуса от Пи / 6 — это 1/2.
Математическая запись:
Способ №2.
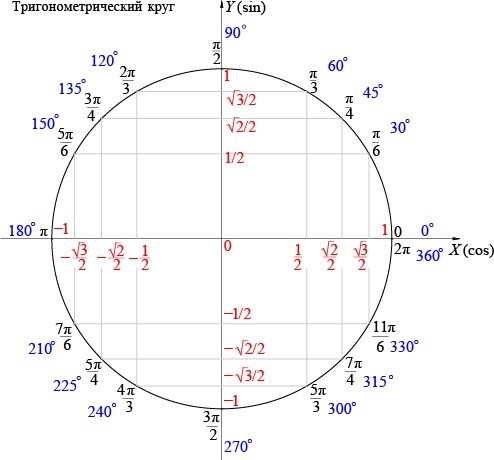
Когда таблица для использования недоступна, значение основных тригонометрических функций от основных аргументов поможет узнать тригонометрическая окружность (или круг).
На тригонометрической окружности все возможные значения синуса располагаются на оси ординат. Рассмотрим вычисление значения синуса от Пи / 6.
Аргумент синуса по заданию равен Пи / 6. На окружности найдем это значение. Чтобы вычислить значение синуса от этого аргумента опустим перпендикуляр на ось Оу и получим значение 1/2. Следовательно, синус от Пи / 6 равен 1/2.
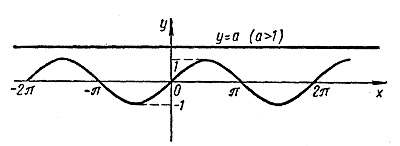
Способ №3.
Без таблицы и тригонометрической окружности также можно найти значение функции по ее графику. Например, по графику синуса (синусоиде) находим значение Пи / 6 на оси Ох и проводим перпендикулярную прямую относительно этой оси к графику. Получаем точку, которую проектируем на ось Оу и получаем значение 1/2.
Таблица синусов.
Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.
Калькулятор — синус угла
sin(°) = 0
Калькулятор — арксинус угла
arcsin() = 90°
Таблица синусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| sin α | 0 | 12 | √22 | √32 | 1 | 0 | -1 | 0 |
Таблица синусов углов от 0° до 180°
| sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107 |
sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 |
sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107 |
sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0.052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
Таблица синусов углов от 181° до 360°
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 |
sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 |
sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 |
sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |
The value of sin pi/6 is 0.5. Sin pi/6 radians in degrees is written as sin ((π/6) × 180°/π), i.e., sin (30°). In this article, we will discuss the methods to find the value of sin pi/6 with examples.
- Sin pi/6: 1/2
- Sin pi/6 in decimal: 0.5
- Sin (-pi/6): -0.5 or -(1/2)
- Sin pi/6 in degrees: sin (30°)
What is the Value of Sin pi/6?
The value of sin pi/6 in decimal is 0.5. Sin pi/6 can also be expressed using the equivalent of the given angle (pi/6) in degrees (30°).
We know, using radian to degree conversion, θ in degrees = θ in radians × (180°/pi)
⇒ pi/6 radians = pi/6 × (180°/pi) = 30° or 30 degrees
∴ sin pi/6 = sin π/6 = sin(30°) = 1/2 or 0.5
Explanation:
For sin pi/6, the angle pi/6 lies between 0 and pi/2 (First Quadrant). Since sine function is positive in the first quadrant, thus sin pi/6 value = 1/2 or 0.5
Since the sine function is a periodic function, we can represent sin pi/6 as, sin pi/6 = sin(pi/6 + n × 2pi), n ∈ Z.
⇒ sin pi/6 = sin 13pi/6 = sin 25pi/6 , and so on.
Note: Since, sine is an odd function, the value of sin(-pi/6) = -sin(pi/6).
Methods to Find Value of Sin pi/6
The sine function is positive in the 1st quadrant. The value of sin pi/6 is given as 0.5. We can find the value of sin pi/6 by:
- Using Trigonometric Functions
- Using Unit Circle
Sin pi/6 in Terms of Trigonometric Functions
Using trigonometry formulas, we can represent the sin pi/6 as:
- ± √(1-cos²(pi/6))
- ± tan(pi/6)/√(1 + tan²(pi/6))
- ± 1/√(1 + cot²(pi/6))
- ± √(sec²(pi/6) — 1)/sec(pi/6)
- 1/cosec(pi/6)
Note: Since pi/6 lies in the 1st Quadrant, the final value of sin pi/6 will be positive.
We can use trigonometric identities to represent sin pi/6 as,
- sin(pi — pi/6) = sin 5pi/6
- -sin(pi + pi/6) = -sin 7pi/6
- cos(pi/2 — pi/6) = cos pi/3
- -cos(pi/2 + pi/6) = -cos 2pi/3
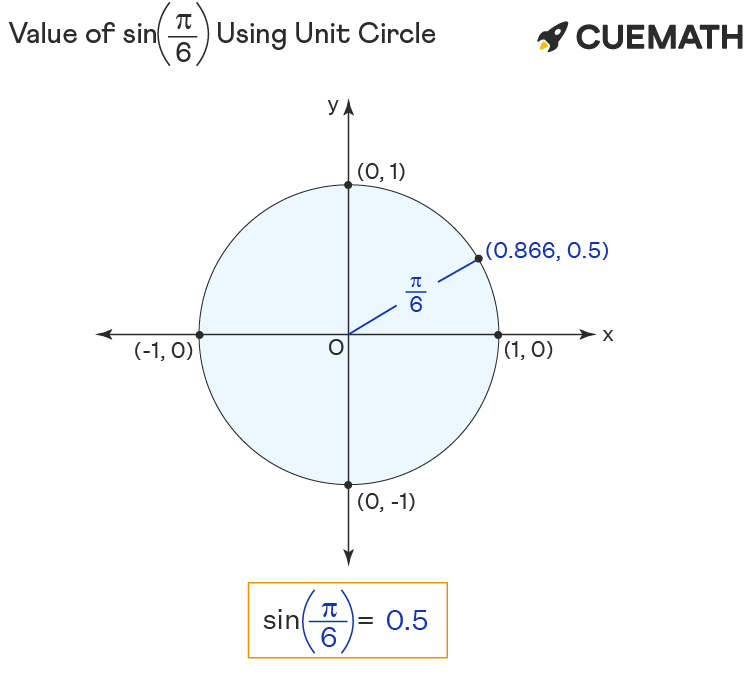
Sin pi/6 Using Unit Circle
To find the value of sin π/6 using the unit circle:
- Rotate ‘r’ anticlockwise to form pi/6 angle with the positive x-axis.
- The sin of pi/6 equals the y-coordinate(0.5) of the point of intersection (0.866, 0.5) of unit circle and r.
Hence the value of sin pi/6 = y = 0.5
☛ Also Check:
- cot pi/8
- cot 3pi/2
- sin 5pi
- sin 5pi/4
- cot pi/2
- tan 5pi/3
FAQs on Sin pi/6
What is Sin pi/6?
Sin pi/6 is the value of sine trigonometric function for an angle equal to pi/6 radians. The value of sin pi/6 is 1/2 or 0.5.
What is the Value of Sin pi/6 in Terms of Cosec pi/6?
Since the cosecant function is the reciprocal of the sine function, we can write sin pi/6 as 1/cosec(pi/6). The value of cosec pi/6 is equal to 2.
How to Find the Value of Sin pi/6?
The value of sin pi/6 can be calculated by constructing an angle of π/6 radians with the x-axis, and then finding the coordinates of the corresponding point (0.866, 0.5) on the unit circle. The value of sin pi/6 is equal to the y-coordinate (0.5). ∴ sin pi/6 = 0.5.
What is the Value of Sin pi/6 in Terms of Cot pi/6?
We can represent the sine function in terms of the cotangent function using trig identities, sin pi/6 can be written as 1/√(1 + cot²(pi/6)). Here, the value of cot pi/6 is equal to 1.7321.
How to Find Sin pi/6 in Terms of Other Trigonometric Functions?
Using trigonometry formula, the value of sin π/6 can be given in terms of other trigonometric functions as:
- ± √(1-cos²(pi/6))
- ± tan(pi/6)/√(1 + tan²(pi/6))
- ± 1/√(1 + cot²(pi/6))
- ± √(sec²(pi/6) — 1)/sec(pi/6)
- 1/cosec(pi/6)
☛ Also check: trigonometric table
Найди верный ответ на вопрос ✅ «Чему равны сos п/6, sin п/6, tg п/6, ctg п/6 …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Алгебра » Чему равны сos п/6, sin п/6, tg п/6, ctg п/6