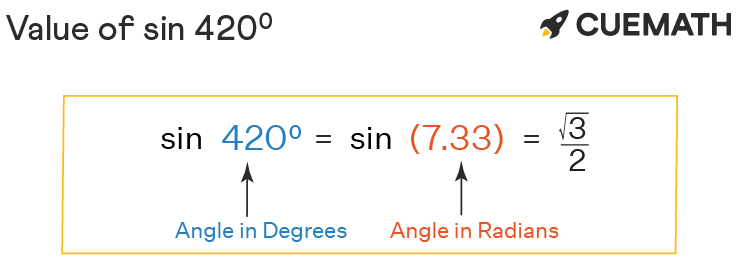
The value of sin 420 degrees is 0.8660254. . .. Sin 420 degrees in radians is written as sin (420° × π/180°), i.e., sin (7π/3) or sin (7.330382. . .). In this article, we will discuss the methods to find the value of sin 420 degrees with examples.
- Sin 420°: 0.8660254. . .
- Sin 420° in fraction: √3/2
- Sin (-420 degrees): -0.8660254. . .
- Sin 420° in radians: sin (7π/3) or sin (7.3303828 . . .)
What is the Value of Sin 420 Degrees?
The value of sin 420 degrees in decimal is 0.866025403. . .. Sin 420 degrees can also be expressed using the equivalent of the given angle (420 degrees) in radians (7.33038 . . .).
We know, using degree to radian conversion, θ in radians = θ in degrees × (pi/180°)
⇒ 420 degrees = 420° × (π/180°) rad = 7π/3 or 7.3303 . . .
∴ sin 420° = sin(7.3303) = √3/2 or 0.8660254. . .
Explanation:
For sin 420°, the angle 420° > 360°. Given the periodic property of the sine function, we can represent it as sin(420° mod 360°) = sin(60°). The angle 420°, coterminal to angle 60°, is located in the First Quadrant(Quadrant I).
Since sine function is positive in the 1st quadrant, thus sin 420 degrees value = √3/2 or 0.8660254. . .
Similarly, sin 420° can also be written as, sin 420 degrees = (420° + n × 360°), n ∈ Z.
⇒ sin 420° = sin 780° = sin 1140°, and so on.
Note: Since, sine is an odd function, the value of sin(-420°) = -sin(420°).
Methods to Find Value of Sin 420 Degrees
The sine function is positive in the 1st quadrant. The value of sin 420° is given as 0.86602. . .. We can find the value of sin 420 degrees by:
- Using Unit Circle
- Using Trigonometric Functions
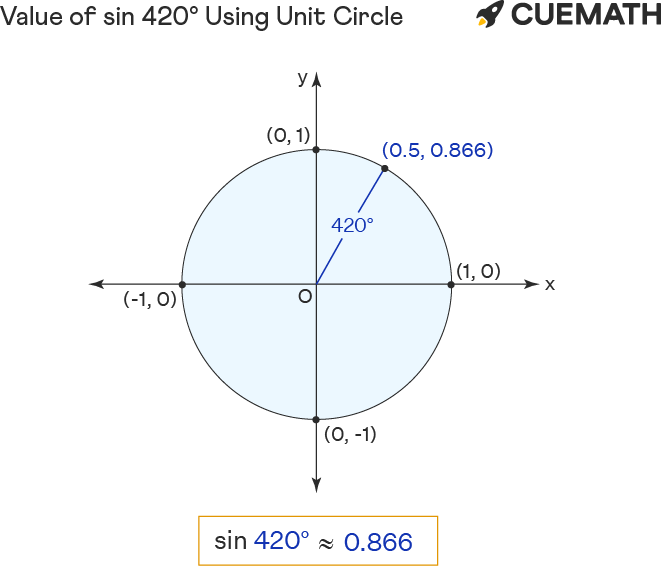
Sin 420 Degrees Using Unit Circle
To find the value of sin 420 degrees using the unit circle, represent 420° in the form (1 × 360°) + 60° [∵ 420°>360°] ∵ sine is a periodic function, sin 420° = sin 60°.
- Rotate ‘r’ anticlockwise to form a 60° or 420° angle with the positive x-axis.
- The sin of 420 degrees equals the y-coordinate(0.866) of the point of intersection (0.5, 0.866) of unit circle and r.
Hence the value of sin 420° = y = 0.866 (approx)
Sin 420° in Terms of Trigonometric Functions
Using trigonometry formulas, we can represent the sin 420 degrees as:
- ± √(1-cos²(420°))
- ± tan 420°/√(1 + tan²(420°))
- ± 1/√(1 + cot²(420°))
- ± √(sec²(420°) — 1)/sec 420°
- 1/cosec 420°
Note: Since 420° lies in the 1st Quadrant, the final value of sin 420° will be positive.
We can use trigonometric identities to represent sin 420° as,
- sin(180° — 420°) = sin(-240°)
- -sin(180° + 420°) = -sin 600°
- cos(90° — 420°) = cos(-330°)
- -cos(90° + 420°) = -cos 510°
☛ Also Check:
- sin 556 degrees
- sin 135 degrees
- sin 35 degrees
- sin 12 degrees
- sin 100 degrees
- sin 70 degrees
FAQs on Sin 420 Degrees
What is Sin 420 Degrees?
Sin 420 degrees is the value of sine trigonometric function for an angle equal to 420 degrees. The value of sin 420° is √3/2 or 0.866 (approx).
What is the Value of Sin 420° in Terms of Cosec 420°?
Since the cosecant function is the reciprocal of the sine function, we can write sin 420° as 1/cosec(420°). The value of cosec 420° is equal to 1.15470.
How to Find Sin 420° in Terms of Other Trigonometric Functions?
Using trigonometry formula, the value of sin 420° can be given in terms of other trigonometric functions as:
- ± √(1-cos²(420°))
- ± tan 420°/√(1 + tan²(420°))
- ± 1/√(1 + cot²(420°))
- ± √(sec²(420°) — 1)/sec 420°
- 1/cosec 420°
☛ Also check: trigonometric table
How to Find the Value of Sin 420 Degrees?
The value of sin 420 degrees can be calculated by constructing an angle of 420° with the x-axis, and then finding the coordinates of the corresponding point (0.5, 0.866) on the unit circle. The value of sin 420° is equal to the y-coordinate (0.866). ∴ sin 420° = 0.866.
What is the Value of Sin 420 Degrees in Terms of Cos 420°?
Using trigonometric identities, we can write sin 420° in terms of cos 420° as, sin(420°) = √(1-cos²(420°)). Here, the value of cos 420° is equal to 0.5.
Адриана
26 февраля, 19:17
-
Севастьяна
26 февраля, 19:33
+1
1) sin 420° = sin (360° + 60°) = sin 60° = √3/2
2) cos 11π/6 = cos (2π — π/6) = cos (-π/6) = cos π/6 = √3/2
3) tg 31π/3 = tg (10π + π/3) = tg π/3 = √3
4) ctg (-330°) = — ctg 330° = — ctg (360° — 30°) = — ctg (-30°) = ctg 30° = √3
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «вычислите: sin420 градусов, cos 11π:6, tg31π:3, ctg (-330 градусов) …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Алгебра » вычислите: sin420 градусов, cos 11π:6, tg31π:3, ctg (-330 градусов)
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
5
1 ответ:
0
0
Ответ:
√3/2
Объяснение:
sin(420)=sin(360+60)=sin(60) =√3/2
Читайте также
(3+√15)(√15-3)=-(3-√15)(3+√15)=-(3^2-(√15)^2)=-(9-15)=-(-6)=6
Пропорция: 200 грн — 100%
230 грн — х%
х = 230 * 100 : 200 = 115% — такой стала цена товара
115% — 100% = 15% — на стiльки вiдсоткiв пiдвищилась цiна товару
Вiдповiдь: пiдвищилась на 15%.
Квадрат первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа равны квадрату разности двух чисел
x² — 2*x*y + y² = (x — y)²
Ответ под номером 5
Ответ: 3.
Когда x->0, мы можем использовать таблицу эквивалентности. Т.е. tgx~x. Тогда lim 3xx = 3;
√2/2(cos a+√2/2sina)(√2/2cosa+√2/2sina)=1/2+1/2sin2a
Таблица синусов.
Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.
Калькулятор — синус угла
sin(°) = 0
Калькулятор — арксинус угла
arcsin() = 90°
Таблица синусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| sin α | 0 | 12 | √22 | √32 | 1 | 0 | -1 | 0 |
Таблица синусов углов от 0° до 180°
| sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107 |
sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 |
sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107 |
sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0.052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
Таблица синусов углов от 181° до 360°
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 |
sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 |
sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 |
sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |
Сомневаетесь в ответе?
Найдите правильный ответ на вопрос ✅ «вычислите: sin420 градусов, cos 11π:6, tg31π:3, ctg (-330 градусов) …» по предмету 📘 Алгебра, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы