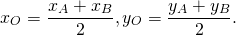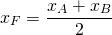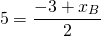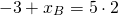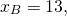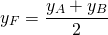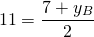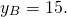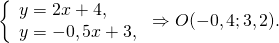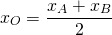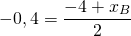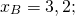Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
Примеры.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Решение:
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
Ответ: (13;15).
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Решение:
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
Ответ: (-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Пример
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Решение:
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
5=-0,5·(-4)+b, откуда b=3.
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Найдём координаты точки пересечения прямых:
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Ответ: (3,2;1,4).
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
| для точки A(x;y) | |
| симметрия относительно: | |
| оси Ox | A1(x;-y) |
| оси Oy | A2(-x;y) |
|
биссектрисы I и II координатных четвертей (прямой y=x) |
A3(y;x) |
|
биссектрисы I b II координатных четвертей (прямой y= -x) |
A4(-y;-x) |
Как построить симметричную точку
Строить симметричные точки учат на уроках геометрии в средней школе. Это умение может в дальнейшем пригодиться на уроках черчения, а также на занятиях в высших учебных заведениях.

Инструкция
Прочитайте условие задачи и определите, относительно чего должна быть симметрична точка. Например, может потребоваться построение точки, симметричной относительно другой точки, оси симметрии, начала координат, оси Ох или Оу и т.п.
Если вам нужно построить точку А1, симметричную А относительно начала координат, сначала определите координаты точки А. А1 будет иметь те же координаты, но с противоположным знаком. Например, А1 (3; -5) будет симметрична А (-3; 5). Найдите и постройте на графике точку А1 с полученными координатами.
Чтобы построить точку А1, симметричную А относительно оси Ох, нужно найти точку с такой же абсциссой, но при этом с ординатой, противоположной по знаку. Это значит, что точке А (х; у) будет симметрична А1 (х; -у). Например, если А имеет координаты 6 по оси Ох и 2 по оси Оу, то вам нужно будет найти и построить точку А1 (6; -2).
Если требуется построить А1, симметричную А относительно оси Оу, найдите А1, ордината которой будет равна А, а абсцисса противоположна абсциссе А по знаку. Это означает, что А1 (-х; у) будет симметрична А (х; у). Например, если дана А (4; 8), то нужно найти и построить А1 (-4; 8).
Если необходимо построить точку А1, симметричную А относительно точки В, то нужно сначала начертить луч из А, проходящий через В. Измерьте расстояние от А до В и постройте точку А1 на таком же расстоянии от В, но в противоположной стороне луча. В результате у вас получится отрезок АА1, центром которого является точка В.
Чтобы построить точку А1, симметричную А относительно прямой, постройте луч с начальной точкой А, пересекающийся с прямой и перпендикулярный ей. Измерьте расстояние от А до точки пересечения прямой и луча, а затем постройте точку А1 на том же расстоянии от прямой, но в противоположной стороне. У вас должен получиться отрезок АА1, который разделен прямой ровно пополам.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание
- Что значит симметричная точка относительно начала координат
- Урок по теме «Симметрия на координатной плоскости»
- Ход урока
- Осевая и центральная симметрия
- Что такое симметрия
- Осевая симметрия
- Центральная симметрия
- Задачи на самопроверку
- Координаты симметричных точек
Что значит симметричная точка относительно начала координат
Построить точку, симметричную точке A(x, y) относительно:
а) оси Ox,
б) оси Oy,
в) начала координат.
Две точки M1 и M2 называются симметричными относительно прямой, если отрезок M1M2 перпендикулярен этой прямой, причем его середина лежит на этой прямой.
Две точки M1 и M2 называются симметричными относительно точки O, если точка O является серединой отрезка M1M2.
а) Точка B, симметричная с точкой A(x, y) относительно оси Ox, имеет абсциссу такую же, как и точка A, а ординату, равную по абсолютной величине ординате точки A, но противоположную ей по знаку. Значит, точка B имеет координаты x и —y: B(x, —y) (см. рисунок).
б) Точка C, симметричная с точкой A(x, y) относительно оси Oy, будет иметь ординату такую же, как и точка A, а абсцисса точки C будет по абсолютной величине равна абсциссе точки A, но противоположна ей по знаку. Значит, точка C имеет координаты —x и y: C(-x, y) (см. рисунок)
в) Точка D, симметричная точке A(x, y) относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате точки A, но противоположные им по знаку, т. е. координаты точки D будут равны —x и —y: D(-x, —y) (см. рисунок).
Источник
Урок по теме «Симметрия на координатной плоскости»
Разделы: Математика
Основные цели урока: тренировать способность к определению координат точек и построению точек по их координатам; выявить взаимосвязь между координатами точек симметричных относительно начала координат и повторить взаимосвязь между координатами точек симметричных относительно координатных осей.
Перед началом урока учитель собирает творческое домашнее задание: на альбомных листах учащиеся оформляли свои рисунки по координатам.
Ход урока
1. Самоопределение к деятельности.
– Я вижу у вас хорошее настроение и боевой настрой. Они нам очень пригодятся. Сегодня у нас пройдёт необычный урок – Морское путешествие. Дело в том, что вчера на сайте нашей школы появился сигнал бедствия от Робинзона Крузо. Он просит помочь ему построить парусник, на котором он смог бы вернуться домой. Чтобы спасти его, нам надо преодолеть большое расстояние. Давайте посмотрим на карту нашего путешествия.
Маршрут: Бухта знаний – Залив Исторический – Остров сокровищ – Школа Робинзона Крузо – Мыс Настроения – Бухта знаний.
– Итак, мы отправляемся в путь, но чтобы не сбиться с маршрута, преодолеть все рифы и подводные течения, нам необходимо внимательно следить за координатами нашего корабля. Давайте вспомним, какую тему мы недавно начали изучать? (Координатная плоскость).
– Чтобы преодолеть залив Исторический и не разбиться о его скалистые берега, давайте вспомним как давно появилось понятие координатной плоскости, и кто впервые ввёл его? ( Рене Декарт.)
– Что вам о нём известно? Тогда давайте обратимся к нашей энциклопедии.
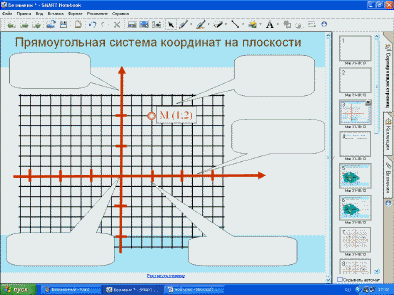
– Из чего же состоит координатная плоскость?
Вызвать ученика. (Весь класс помогает: две пересекающиеся под прямым углом прямые – оси абсцисс и ординат, точка их пересечения – начало отсчёта, стрелочки – указывают положительное направление осей, единичный отрезок.) Ученик заполняет маркером пустые места на координатной плоскости. Оценка.
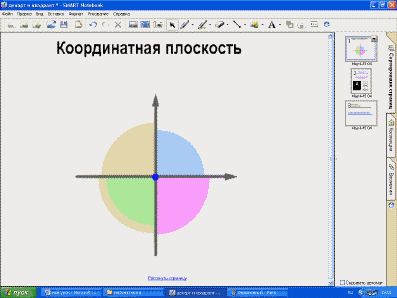
– Сколько углов образовалось при построении координатной плоскости? (четыре) Как они называются? (координатные углы или координатные четверти). Покажите, как они расположены.
Ученик нумерует маркером углы и указывает координаты точек в этих углах схематично с помощью знаков “+” и “-”.
– Как с помощью неравенств записать знаки координат точек в каждом из углов? Ученики обсуждают в парах и предлагают свои варианты, из которых выбирается верный.
I. x>0, y>0
II. x 0
III. x 0, y 27.01.2012
Источник
Осевая и центральная симметрия
О чем эта статья:
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Источник
Координаты симметричных точек
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
Источник
Координаты симметричных точек
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
- Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
- Найти точку O пересечения прямых f и g.
- Зная конец отрезка A и его середину O найти другой конец B.
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
Осевая и центральная симметрия
О чем эта статья:
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Дробно-линейные отображения
Дробно-линейной функцией называется функция вида: , где — произвольные комплексные числа, такие, что .
Перечислим без доказательства свойства дробно-линейной функции.
- Дробно-линейная функция осуществляет взаимно однозначное отображение расширенной комплексной плоскости на себя. При этом точка отображается в точку , а точка отображается в .
- Дробно-линейное отображение можно представить в виде суперпозиции трех простейших отображений: целого линейного , отображения и сдвига .
- Дробно-линейное отображение отображает окружности и прямые в окружности и прямые. При этом прямая может перейти как в прямую, так и в окружность. Окружность тоже может перейти как в прямую, так и в окружность. Это свойство называется круговым свойством дробно-линейных отображений.
- Точки симметричные относительно прямой или окружности переходят в точки симметричные относительно образа этой прямой или окружности.
- Дробно-линейное отображение, переводящее три заданные точки в три заданные точки: дается формулой:
Пример 1 Найти образ мнимой оси при отображении .
Мнимая ось представляет собой прямую. По третьему свойству она должна перейти в окружность или в прямую. Найдем образы трех точек мнимой оси: . Так как образ одной из точек , то мнимая ось переходит в прямую проходящую через и , то есть в действительную ось.
Пример 2 Найти дробно линейное отображение, переводящее точки .
Пример 3 Найти образ области при отображении
Найдем образ мнимой оси при данном отображении. Возьмем три точки : .
Отметим также, что . Куда же перешел луч ? Подставим в формулу отображения: . При , точки переходят в точки луча действительной оси. Точки переходят в луч . Образы двух точек действительной оси у нас есть: Действительная ось переходит в окружность, проходящую через точки .
Найдем образ точки из границы нашей области:
Итак, образ луча будет полуокружность .
Теперь мы можем изобразить схему самого отображения:
Пример 4 Найти образы всех квадрантов при отображении .
Чтобы не решать опять задачи подобные примеру 3, воспользуемся следствием принципа симметрии Римана-Шварца в такой формулировке:
Пусть функция отображает область в и — дуга окружности или отрезок, принадлежащий границе области , и — область, симметричная относительно .
Пусть непрерывна на и области и не пересекаются. Тогда функция конформно отображает на , где и — образы и соответственно при отображении .
На следующем рисунке видно, что области и симметричны относительно луча , который переходит в полуокружность . Так находится образ области . Он для удобства обозначен штриховкой. Точно так же находятся образы остальных двух квадрантов.
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Нужна помощь с курсовой или дипломной работой?
http://skysmart.ru/articles/mathematic/osevaya-i-centralnaya-simmetriya
http://khab.work5.ru/spravochnik/matematika/drobno-linejnye-otobrazheniya
Оборудование:
- SMART-BOARD.
- ПК “КМ-школа”.
- Мультимедийный проектор.
- Индивидуальные планшетки, маркер, ватный диск
(для удаления и исправления записей). - Два листа А4 на каждой парте для работы в группах
и в парах. - Изображение парусника на миллиметровой бумаге
для самостоятельной работы в двух вариантах.
Основные цели урока: тренировать
способность к определению координат точек и
построению точек по их координатам; выявить
взаимосвязь между координатами точек
симметричных относительно начала координат и
повторить взаимосвязь между координатами точек
симметричных относительно координатных осей.
Перед началом урока учитель собирает
творческое домашнее задание: на альбомных листах
учащиеся оформляли свои рисунки по координатам.
Ход урока
1. Самоопределение к деятельности.
– Здравствуйте, ребята!
– Я вижу у вас хорошее настроение и
боевой настрой. Они нам очень пригодятся. Сегодня
у нас пройдёт необычный урок – Морское
путешествие. Дело в том, что вчера на сайте нашей
школы появился сигнал бедствия от Робинзона
Крузо. Он просит помочь ему построить парусник,
на котором он смог бы вернуться домой. Чтобы
спасти его, нам надо преодолеть большое
расстояние. Давайте посмотрим на карту нашего
путешествия.
Маршрут: Бухта знаний – Залив
Исторический – Остров сокровищ – Школа
Робинзона Крузо – Мыс Настроения – Бухта знаний.
– Итак, мы отправляемся в путь, но
чтобы не сбиться с маршрута, преодолеть все рифы
и подводные течения, нам необходимо внимательно
следить за координатами нашего корабля. Давайте
вспомним, какую тему мы недавно начали изучать?
(Координатная плоскость).
– Чтобы преодолеть залив Исторический
и не разбиться о его скалистые берега, давайте
вспомним как давно появилось понятие
координатной плоскости, и кто впервые ввёл его? (
Рене Декарт.)
– Что вам о нём известно? Тогда давайте
обратимся к нашей энциклопедии.
– Из чего же состоит координатная
плоскость?
Вызвать ученика. (Весь класс помогает:
две пересекающиеся под прямым углом прямые – оси
абсцисс и ординат, точка их пересечения – начало
отсчёта, стрелочки – указывают положительное
направление осей, единичный отрезок.) Ученик
заполняет маркером пустые места на координатной
плоскости. Оценка.
– Сколько углов образовалось при
построении координатной плоскости? (четыре) Как
они называются? (координатные углы или
координатные четверти). Покажите, как они
расположены.
Ученик нумерует маркером углы и
указывает координаты точек в этих углах
схематично с помощью знаков “+” и “-”.
– Как с помощью неравенств записать
знаки координат точек в каждом из углов? Ученики
обсуждают в парах и предлагают свои варианты, из
которых выбирается верный.
I. x>0, y>0
II. x<0, y>0
III. x<0, y<0
IV. x>0, y<0.
– А каким углам принадлежат точки,
лежащие на осях координат? (Никаким)
– Молодцы! А кто знает третье название
координатных углов? (?)
– Ответить на этот вопрос нам поможет
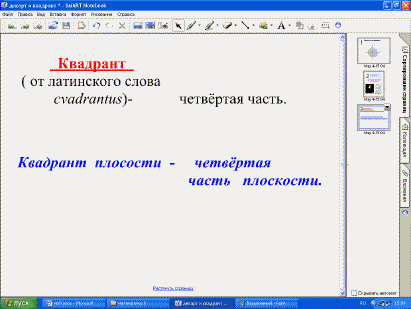
ребус:
– Какое слово зашифровано? (Квадрант).
Что оно означает? (?) Снова обратимся к
энциклопедии.
Записать новое слово в словарик.
– Мы много говорим о координатной
плоскости. А для чего нужна координатная
плоскость? (Строить точки по координатам и
наоборот – находить координаты точек.)
– Назовите алгоритм построения точки
в координатной плоскости. ( На оси абсцисс найти
число х и провести через неё вертикальную
пунктирную линию, отметить на оси ординат число у
и провести через неё горизонтальную пунктирную
линию; точка их пересечения и есть искомая точка,
которая обозначается заглавной латинской
буквой.)
– Молодцы. Я вижу вы хорошо усвоили
теоретический материал. Давайте проверим ваши
знания на практике. Тем временем мы приплыли к
острову сокровищ, где спрятаны сокровища
капитана Флинта. С их помощью мы добудем средства
на строительство парусника. Приготовьте
планшетки и маркеры. Устная работа (фронтально).
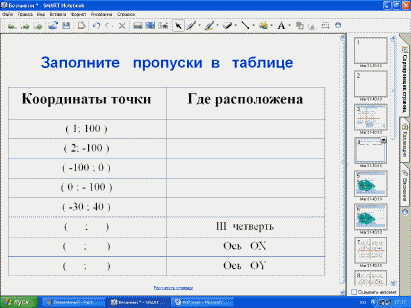
- Заполните пропуски в таблице. (дети пишут
ответы на планшетках, учитель проверяет и
записывает правильные ответы в таблицу на доске)
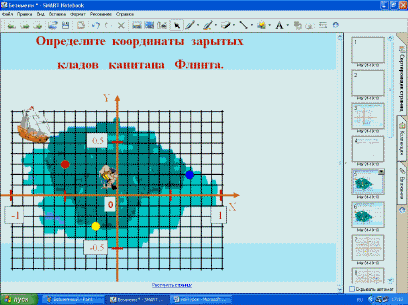
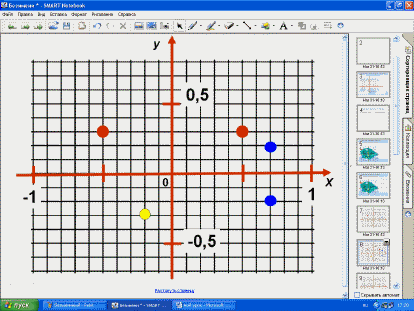
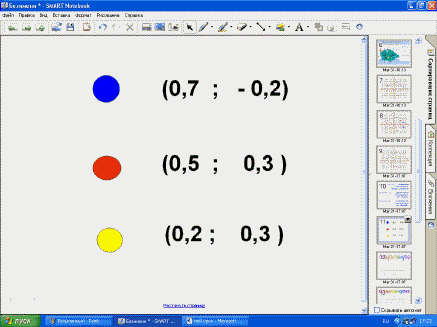
- Запишите координаты точек, в которых зарыты
сокровища капитана Флинта и координатные
четверти, в которых они расположены в порядке:
синяя, красная, жёлтая.
(Ответы будут поочерёдно появляться на
доске)
- Не выполняя построения, запишите координаты
точек симметричных данным относительно:
оси абсцисс (синяя)
оси ординат (красная)
– Проверим.
– Относительно начала координат
(жёлтая)
Последнее задание вызовет
затруднение.
– Почему возникло затруднение? (Не
умеем строить точки симметричные относительно
начала координат)
– Давайте попробуем выйти из этого
затруднительного положения.
– Как вы думаете, над какой темой мы сегодня
будем работать? (Симметрия на координатной
плоскости относительно начала координат).
– Откройте тетради, запишите число, классная
работа и тема урока “Симметрия на координатной
плоскости относительно начала координат”.
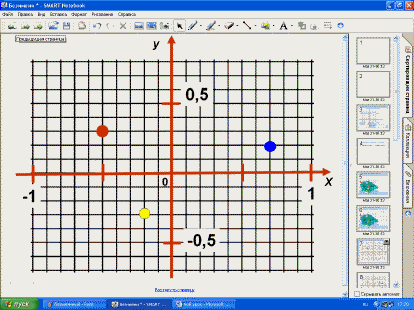
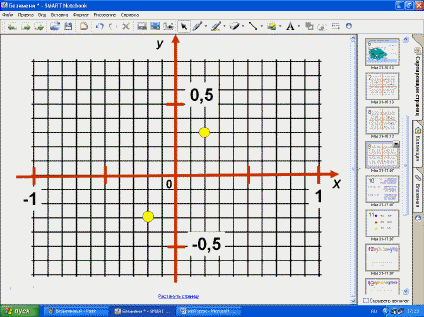
– Как расположены на оси абсцисс числа
0,2 и -0,2? (Равноудалены от начала координат и
симметричны относительно начала координат).
– Как расположены на оси ординат числа
0,3 и -0,3? (Равноудалены от начала координат и
симметричны относительно начала координат).
– Какой можно сделать вывод? (Точки
симметричны относительно начала координат).
– На чём основывался ваш вывод? (Так
как первые и вторые координаты симметричны
относительно начала координат, то точки
симметричны относительно начала координат).
– Чем отличаются координаты точек
симметричных относительно начала координат? (Они
являются противоположными числами)
– Как в общем виде записать координаты
точек симметричных относительно начала
координат? Работа в группах – 1 минута.
Учитель выборочно опрашивает
учащихся.
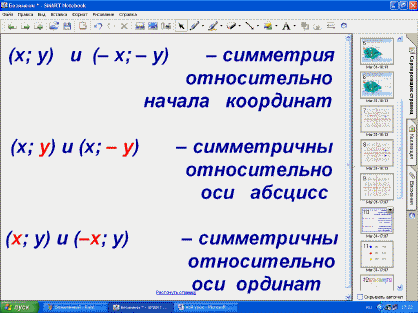
В результате приходят к выводу: (x; y)
и (– x; – y).
Вывод появляется на доске в виде слайда.
– Запишите их в тетрадь.
– Давайте вернёмся к нашим кладам и отметим
координаты точек, симметричных для них.
– Поднимите руку, кто построил верно? Кто
допустил ошибку? В чём причина ошибки? (……)
Запишите координаты точек в тетрадь:
– Мы хорошо потрудились, но нам предстоит
выполнить очень ответственное задание
–строительство парусника. Давайте физически к
этому подготовимся.
Физкультминутка.
Расправьте плечи. Вдох. Выдох.
Да – опустить голову вниз, нет – голову назад.
Точка (6;0) – лежит на оси абсцисс – да.
Точка (0; -2) –лежит на оси абсцисс – нет.
Точка (0;0) –начало координат – да.
Ось абсцисс лежит в первой четверти – нет.
Ось ординат лежит в четвёртой четверти – нет.
Да –голову вправо, нет – голову влево.
Сегодня мы изучаем симметрию – да.
Абсциссу точки записывают второй координатой
– нет.
Ординату точки записывают первой координатой
– нет.
Координаты точки записывают в круглых скобках,
через точку с запятой – да.
Мы приближаемся к острову Робинзона Крузо, где
нам предстоит построить для него парусник.
– Запишите в тетрадях – самостоятельная
работа ( Работа выполняется на миллиметровой
бумаге – по вариантам. На листочках изображён
один парусник, но в разных координатных
четвертях: первый вариант – в первой
координатной четверти, второй вариант – во
второй).
Самостоятельная работа ( 8-10 мин.):
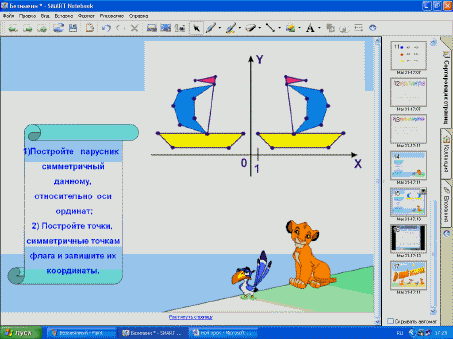
1. Постройте точки парусника, симметричные
данному по заданным координатам
относительно оси ординат.
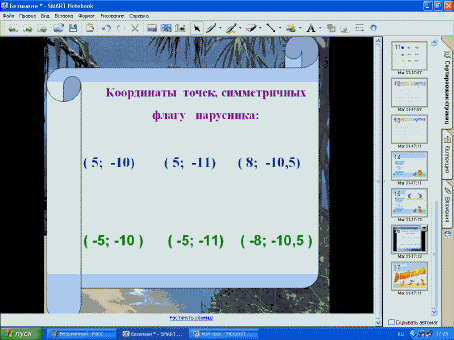
2. Запишите точки, симметричные точкам флага
исходного парусника относительно начала
координат в тетрадь.
– Сдайте работу на миллиметровой бумаге.
– Давайте сверим результаты.
– Поднимите руки, у кого такой же рисунок?
– У кого другой? Почему?
– Сравните координаты флага.
Вопросы рефлексии:
- Что нового узнали?
- На каких знаниях вы основывались для открытия
нового знания? - Как же записать координаты симметричных точек
относительно начала координат? - Кто считает, что хорошо усвоил тему?
- Кому ещё надо поработать дома?
Домашнее задание:
Учебник Математика 5 Петерсон Л.Г. Глава 3, параграф 4, п.1 № 177 (а) –
построить четырёхугольник по координатам и
построить ему симметричный относительно оси
абсцисс; № 201 (а или б).
Презентация