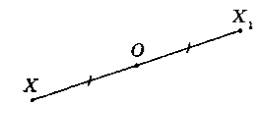Содержание
- Определение симметричного треугольника
- Особенности симметричных треугольников
- Как найти точку симметрии треугольника
- Как вычислить площадь симметричного треугольника
- Простое правило вычисления площади
- Пример вычисления площади
- Таблица для вычисления площади
- Примеры симметричных треугольников в естественном мире
- Вопрос-ответ
- Что такое симметричный треугольник?
- Как узнать, является ли треугольник симметричным?
- Какие примеры симметричных треугольников можно назвать?
- Можно ли определить симметричность треугольника по его центру тяжести?
- Есть ли у симметричного треугольника особенные свойства?
- Каким образом можно отличить равнобедренный треугольник от симметричного?
Если вы занимаетесь геометрией и хотите научиться определять, является ли треугольник симметричным, то эта статья для вас. Симметричный треугольник — это треугольник, который может быть разделен на две одинаковые части по линии симметрии. Это свойство находит широкое применение в различных сферах, таких как архитектура, дизайн, и даже в природе.
Узнавать симметричность треугольника можно не только визуально. Часто для определения применяются специальные правила и формулы. В данной статье мы рассмотрим несколько таких правил, которые помогут вам легко определить, симметричен ли треугольник или нет.
Пример: многие знаки зодиака, такие как Скорпион, Близнецы, Рак, имеют симметричную форму, что делает их узнаваемыми и привлекательными с точки зрения дизайна.
Определение симметричного треугольника
Симметричным треугольником называется треугольник, у которого все стороны равны и все углы равны 60 градусов. Такой треугольник является особым, так как он обладает свойством симметрии, то есть имеет одинаковые зеркально симметричные части.
Определить симметричный треугольник можно несколькими способами. Во-первых, измерив все его стороны и углы и проверив, что они действительно равны соответственно 60 градусов. Во-вторых, можно воспользоваться геометрическими свойствами симметричного треугольника, например, его осевой симметрией и центром симметрии.
Для построения симметричного треугольника необходимо использовать геометрический циркуль, который поможет нарисовать равные стороны и углы. Также можно воспользоваться таблицей соответствий для нахождения координат вершин треугольника и его осевой симметрии.
Симметричные треугольники возникают в различных областях математики, физики, геометрии и искусства, и являются важным объектом изучения.
Особенности симметричных треугольников
Симметричный треугольник — это фигура, которая имеет три равных стороны и три равных угла. Такие треугольники имеют множество особенностей, которые можно использовать для их определения.
- Симметричные треугольники имеют центр симметрии, который находится в точке пересечения медиан.
- Любая прямая, проходящая через центр симметрии, делит треугольник на две равные части.
- Радиус вписанной окружности в симметричном треугольнике равен половине длины любой из сторон.
- Радиус описанной окружности в симметричном треугольнике равен $$frac{a}{2sinA}.$$
Определять симметричный треугольник можно по любому из указанных признаков. Наличие всех указанных особенностей говорит о том, что треугольник симметричный.
Как найти точку симметрии треугольника
Точка симметрии треугольника — это точка, которая делит треугольник на две равные половины. Найти точку симметрии треугольника можно описав ее координатами.
Для правильного треугольника точка симметрии находится в пересечении медиан, то есть линий, проведенных из вершины треугольника в середину противоположной стороны. Для неправильного треугольника точка симметрии может находиться в другом месте.
Для нахождения координат точки симметрии треугольника можно воспользоваться формулами:
- для координат x: (x1 + x2 + x3) / 3;
- для координат y: (y1 + y2 + y3) / 3,
где x1, x2, x3, y1, y2, y3 — координаты вершин треугольника. Также можно воспользоваться таблицей координат и провести несколько простых математических операций.
| № | x | y |
|---|---|---|
| 1 | 3 | 1 |
| 2 | 6 | 4 |
| 3 | 2 | 7 |
Для данного треугольника координаты точки симметрии будут:
- для координат x: (3 + 6 + 2) / 3 = 3.67;
- для координат y: (1 + 4 + 7) / 3 = 4.
Таким образом, точка симметрии треугольника с данными координатами (3.67, 4).
Как вычислить площадь симметричного треугольника
Простое правило вычисления площади
Для вычисления площади симметричного треугольника можно использовать простое правило:
- Определить длину одной стороны треугольника (a).
- Вычислить высоту треугольника (h), проведенную к этой стороне.
- Умножить длину стороны (a) на высоту (h) и разделить полученный результат на 2.
Таким образом, площадь симметричного треугольника равна:
S = (a * h) / 2
Пример вычисления площади
Предположим, что мы знаем длину одной стороны симметричного треугольника:
- a = 6 см
Чтобы вычислить площадь треугольника, нам необходимо найти высоту, так как она не задана явно. Предположим, что мы знаем угол между этой стороной и высотой (60 градусов).
Тогда, чтобы найти высоту, мы можем использовать следующую формулу:
h = a * sin(60°)
Подставив значение стороны (a), получим:
h = 6 см * sin(60°) ≈ 5,20 см
Теперь мы можем вычислить площадь симметричного треугольника:
S = (6 см * 5,20 см) / 2 ≈ 15,60 см²
Таблица для вычисления площади
Для упрощения вычисления площади симметричного треугольника можно использовать таблицу значений:
| Длина стороны (a) | Высота (h) | Площадь (S) |
|---|---|---|
| 3 см | 2,60 см | 3,90 см² |
| 4 см | 3,46 см | 6,92 см² |
| 5 см | 4,33 см | 10,83 см² |
Примеры симметричных треугольников в естественном мире
1. Кристаллы. В кристаллах можно обнаружить симметричные треугольники. Например, в некоторых кристаллах соляной кислоты вы можете увидеть симметричный треугольник на поверхности.
2. Шестиугольная сетка пчелиных сот. Для создания меда пчелы строят соты в форме шестиугольников, но их стенки также образуют симметричные треугольники.
3. Раковины морских улиток. Многие морские улитки имеют раковины, которые содержат симметричные треугольные узоры.
4. Лепестки цветов. Некоторые цветы, такие как осенние гортензии, могут иметь лепестки в форме симметричного треугольника, если посмотреть на них сверху.
5. Снежинки. В сильные морозы можно увидеть настоящие произведения искусства природы — симметричные снежинки с шестиугольной симметрией.
Вопрос-ответ
Что такое симметричный треугольник?
Симметричный треугольник — это треугольник, у которого все стороны и углы равны. Так же у него есть центр симметрии, в котором пересекаются все оси симметрии треугольника.
Как узнать, является ли треугольник симметричным?
Если все стороны треугольника равны, значит, треугольник симметричный. Если же стороны не равны, то можно посмотреть на углы: если в треугольнике все углы равны, то он тоже симметричен. Также можно определить центр симметрии и оси симметрии, но для этого нужно провести специальные линии и посчитать углы.
Какие примеры симметричных треугольников можно назвать?
Примеры симметричных треугольников: равносторонний треугольник, равнобедренный треугольник с углами 60 градусов, равнобедренный треугольник с углами 45 градусов, равнобедренный треугольник с углами 36 градусов. Но также может быть любой другой треугольник, у которого все стороны и углы равны.
Можно ли определить симметричность треугольника по его центру тяжести?
Нет, центр тяжести треугольника не связан с его центром симметрии. Центр тяжести — это точка пересечения линий, проведенных из вершин треугольника в центры противолежащих сторон. Центр симметрии — это точка, в которой пересекаются все оси симметрии треугольника.
Есть ли у симметричного треугольника особенные свойства?
Да, у симметричного треугольника есть несколько особенных свойств. Например, его высоты, биссектрисы и медианы пересекаются в одной точке — центре симметрии. Также все углы симметричного треугольника равны 60 градусов, а его площадь можно вычислить по формуле S=(a^2*sqrt(3))/4, где a — длина стороны треугольника.
Каким образом можно отличить равнобедренный треугольник от симметричного?
Равнобедренный треугольник — это треугольник, у которого две стороны равны. Симметричный треугольник — это треугольник, у которого все три стороны равны. То есть, если у треугольника две равные стороны и третья сторона не равна им, то это равнобедренный треугольник. Если же все три стороны равны, то это симметричный треугольник.
Изучение симметричных форм является одной из важнейших тем в геометрии, а треугольник является символом этой дисциплины. Симметрия – это особое свойство, которое возвращает фигуру к своему исходному состоянию при повороте, отражении или их сочетании. В случае с треугольниками, наличие симметрии можно определить по наличию осевой или плоскостной симметрии.
Осевая симметрия в треугольнике означает, что фигура имеет линию симметрии, относительно которой одна часть симметрична другой. Плоскостная симметрия означает, что фигура имеет симметрию относительно плоскости, которая делит фигуру на две равные части. Определение симметричного треугольника – процесс, который требует внимательного анализа фигуры, чтобы отметить все эти особые характеристики.
В статье предлагается ознакомиться с несколькими примерами и методами определения симметричных треугольников. Помимо того, как узнать, является ли треугольник симметричным, будут представлены и некоторые задачи, которые помогут лучше понять, как работает симметрия в геометрии. Кроме того, вы узнаете, как применять знания о симметрии при решении конкретных задач и какие эффекты возникают, когда треугольники не обладают свойством симметричности.
Содержание
- Что такое симметричный треугольник?
- Свойства симметричного треугольника
- Способы определения симметричности треугольника
- Примеры задач на определение симметричности треугольника
- Вопрос-ответ
- Как определить симметричный треугольник?
- Какие методы можно использовать для определения симметричного треугольника?
- Какие характеристики имеет симметричный треугольник?
- Можно ли определить симметричный треугольник без измерения сторон?
- Какой пример треугольника является симметричным?
Что такое симметричный треугольник?
Симметричный треугольник – это треугольник, у которого все три стороны, углы и медианы являются равными друг другу. Также его можно определить как треугольник, который имеет одну ось симметрии, относительно которой можно разделить его на две части, совершенно задаваемые друг другу.
Симметричный треугольник имеет три вершины, которые расположены на одинаковом расстоянии друг от друга, от центра треугольника до любой из вершин. Также такой треугольник называют равносторонним.
Особенности симметричных треугольников часто привлекают внимание ученых, инженеров и дизайнеров, как символ гармонии и баланса в природе и искусстве. Симметричность является признаком совершенства, порядка и красоты.
- Симметричный треугольник имеет все три стороны равными.
- Симметричный треугольник имеет все углы равными.
- Симметричный треугольник имеет все медианы равными.
Свойства симметричного треугольника
Симметричный треугольник имеет ряд особенностей, которые помогают определить его сразу:
- Равные стороны — у симметричного треугольника все три стороны имеют одинаковую длину.
- Равные углы — углы между сторонами симметричного треугольника также все равны. Это означает, что если один из углов равен 60 градусов, то все углы равны 60 градусов.
- Центр симметрии — у симметричного треугольника есть центр симметрии, вокруг которого он поворачивается без изменения своей формы. Это означает, что если нарисовать линию от центра симметрии к середине каждой стороны треугольника, то эти линии будут пересекаться в одной точке — это и будет центром симметрии.
Зная эти свойства, можно определить симметричный треугольник даже по внешнему виду, без измерения углов и сторон.
Способы определения симметричности треугольника
Симметрия в треугольнике – это свойство геометрической фигуры, при котором ее две половины, отраженные по некоторой оси, совпадают. Существует несколько способов определения симметричности треугольника.
- Метод отрезков: В симметричном треугольнике отрезок, соединяющий вершину с центром описанной окружности, будет являться осью симметрии. Поэтому, если задан описанный окружности, можно построить линию, проходящую через вершину и центр окружности, и проверить, делит ли эта линия треугольник на две симметричные половины.
- Метод углов: Симметричный треугольник имеет равные углы и равные стороны. Для проверки равных углов можно измерить каждый угол с помощью градусника или простого угломера. Если все три угла будут равны между собой, то треугольник симметричен.
- Метод сторон: Симметричный треугольник имеет равные стороны. Для проверки равенства сторон можно измерить длину каждой стороны с помощью линейки и сравнить их между собой. Если все три стороны будут равны друг другу, то треугольник симметричен.
Примеры задач на определение симметричности треугольника
Один из наиболее распространенных вопросов, связанных с треугольниками, состоит в том, как определить, является ли треугольник симметричным. Вот несколько примеров задач на эту тему:
- Пример 1: Нарисуйте треугольник со сторонами длиной 4, 5 и 6 см. Является ли он симметричным?
- Пример 2: Найти значения углов треугольника с вершинами в точках (0,0), (4,0) и (2,4). Является ли треугольник симметричным относительно какой-либо оси?
- Пример 3: Постройте треугольник с углами 60 градусов, 60 градусов и 60 градусов, используя компас и линейку. Является ли он симметричным?
В каждом из этих примеров необходимо проанализировать симметричность треугольника относительно определенной оси и определить, является ли он симметричным. Эта задача может потребоваться на экзамене по геометрии или математике, а также на задании домашнего задания для учеников школы или студентов университета.
Вопрос-ответ
Как определить симметричный треугольник?
Симметричный треугольник – это треугольник, у которого все три стороны равны, а все три угла равны 60 градусов. Для определения симметричности треугольника необходимо произвести измерение длины все трех его сторон и проверить, будут ли все они равными.
Какие методы можно использовать для определения симметричного треугольника?
Для определения симметричного треугольника можно использовать различные методы, такие как измерение длин сторон с помощью линейки или ленты, вычисление углов с помощью угломера или использование геометрических формул.
Какие характеристики имеет симметричный треугольник?
Симметричный треугольник имеет три равные стороны, три равных угла по 60 градусов, точку пересечения высот, равные биссектрисы и медианы, а также центр описанной окружности находится в точке пересечения медиан.
Можно ли определить симметричный треугольник без измерения сторон?
Да, можно. Если треугольник имеет три равных угла, то он является равносторонним и симметричным. Также можно определить симметричный треугольник по совпадению его трех биссектрис.
Какой пример треугольника является симметричным?
Примером симметричного треугольника может служить любой равносторонний треугольник, у которого все три стороны равны.
Осевая и центральная симметрия
О чем эта статья:
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Осевая симметрия
Осевая симметрия — это симметрия относительно прямой.
Пусть дана некоторая прямая g.
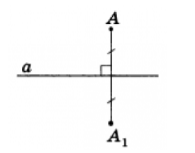
Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:
1) Провести из точки A к прямой g перпендикуляр AO.
2) На продолжении перпендикуляра с другой стороны от прямой g отложить отрезок OA1, равный отрезку AO: OA1=AO.
Полученная точка A1 симметрична точке A относительно прямой g.
Прямая g называется осью симметрии.
Таким образом, точки A и A1 симметричны относительно прямой g, если эта прямая проходит через середину отрезка AA1 и перпендикулярна к нему.
Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A.
Преобразование фигуры F в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.
Фигуры F и F1 называются фигурами, симметричными относительно прямой g.
Чтобы построить треугольник, симметричный данному относительно прямой g, достаточно построить точки, симметричные вершинам треугольника, и соединить их отрезками.
Например, треугольники ABC и A1B1C1 симметричны относительно прямой g.
Если преобразование симметрии относительно прямой g переводит фигуру в себя, то такая фигура называется симметричной относительно прямой g, а прямая g называется её осью симметрии.
Симметричная фигура своей осью симметрии делится на две равные половины. Если симметричную фигуру нарисовать на бумаге, вырезать и согнуть по оси симметрии, то эти половинки совпадут.
Примеры фигур, симметричных относительно прямой.
1) Прямоугольник.
Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно сторонам.
Ромб имеет две оси симметрии:
прямые, на которых лежат его диагонали.
3) Квадрат, как ромб и прямоугольник, имеет четыре оси симметрии: прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.
Окружность имеет бесконечное множество осей симметрии:
любая прямая, содержащая диаметр, является осью симметрии окружности.
Прямая также имеет бесконечное множество осей симметрии: любая перпендикулярная ей прямая является для данной прямой осью симметрии.
Равнобедренная трапеция — фигура, симметричная относительно прямой,перпендикулярной основаниям и проходящей через их середины.
Равнобедренный треугольник имеет одну ось симметрии:
прямую, проходящую через высоту (медиану, биссектрису), проведённую к основанию.

Равносторонний треугольник имеет три оси симметрии:
прямые, содержащие его высоты (медианы, биссектрисы).
Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.
Осевая симметрия является движением.
Осевая и центральная симметрия
Вы будете перенаправлены на Автор24
Понятие движения
Разберем сначала такое понятие как движение.
Отображение плоскости называется движением плоскости, если при этом отображении сохраняются расстояния.
Существуют несколько теорем, связанных с этим понятием.
Отрезок, при движении, переходит в равный ему отрезок.
Треугольник, при движении, переходит в равный ему треугольник.
Любая фигура, при движении, переходит в равную ей фигуру.
Осевая и центральная симметрия являются примерами движения. Рассмотрим их более подробно.
Осевая симметрия
Точки $A$ и $A_1$ называются симметричными относительно прямой $a$, если эта прямая перпендикулярна к отрезку $_1$ и проходит через его центр (рис. 1).
Рассмотрим осевую симметрию на примере задачи.
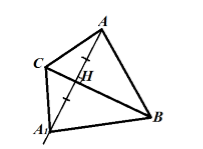
Построить симметричный треугольник для данного треугольника относительно какой-либо его стороны.
Решение.
Пусть нам дан треугольник $ABC$. Будем строить его симметрию относительно стороны $BC$. Сторона $BC$ при осевой симметрии перейдет в саму себя (следует из определения). Точка $A$ перейдет в точку $A_1$ следующим образом: $_1bot BC$, $_1$. Треугольник $ABC$ перейдет в треугольник $A_1BC$ (Рис. 2).
Фигура называется симметричной относительно прямой $a$, если каждая симметричная точка этой фигуры содержится на этой же фигуре (рис. 3).
Готовые работы на аналогичную тему
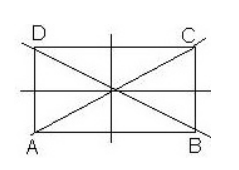
На рисунке $3$ изображен прямоугольник. Он обладает осевой симметрией относительно каждого своего диаметра, а также относительно двух прямых, которые проходят через центры противоположных сторон данного прямоугольника.
Центральная симметрия
Точки $X$ и $X_1$ называются симметричными относительно точки $O$, если точка $O$ является центром отрезка $_1$ (рис. 4).
Рассмотрим центральную симметрию на примере задачи.
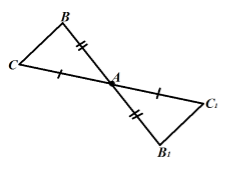
Построить симметричный треугольник для данного треугольника какой-либо его вершины.
Решение.
Пусть нам дан треугольник $ABC$. Будем строить его симметрию относительно вершины $A$. Вершина $A$ при центральной симметрии перейдет в саму себя (следует из определения). Точка $B$ перейдет в точку $B_1$ следующим образом $_1$, а точка $C$ перейдет в точку $C_1$ следующим образом: $_1$. Треугольник $ABC$ перейдет в треугольник $_1C_1$ (Рис. 5).
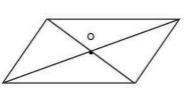
Фигура является симметричной относительно точки $O$, если каждая симметричная точка этой фигуры содержится на этой же фигуре(рис. 6).
На рисунке $6$ изображен параллелограмм. Он обладает центральной симметрией относительно точки пересечения его диагоналей.
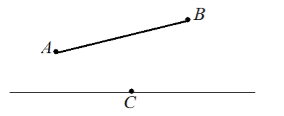
Пусть нам дан отрезок $AB$. Построить его симметрию относительно прямой $l$, не пересекающий данный отрезок и относительно точки $C$, лежащей на прямой $l$.
Решение.
Изобразим схематически условие задачи.
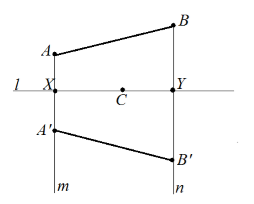
Изобразим для начала осевую симметрию относительно прямой $l$. Так как осевая симметрия является движением, то по теореме $1$, отрезок $AB$ отобразится на равный ему отрезок $A’B’$. Для его построение сделаем следующее: проведем через точки $A и B$ прямые $m и n$, перпендикулярно прямой $l$. Пусть $mcap l=X, ncap l=Y$. Далее проведем отрезки $A’X=AX$ и $B’Y=BY$.
Изобразим теперь центральную симметрию относительно точки $C$. Так как центральная симметрия является движением, то по теореме $1$, отрезок $AB$ отобразится на равный ему отрезок $A»B»$. Для его построения сделаем следующее: проведем прямые $AC и BC$. Далее проведем отрезки $A^<»>C=AC$ и $B^<»>C=BC$.
http://spravochnick.ru/matematika/formuly_parallelogramma_trapecii_kvadrata_pryamougolnika_i_romba/osevaya_i_centralnaya_simmetriya/
Осевая симметрия — это симметрия относительно прямой.

Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:
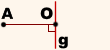

Полученная точка A1 симметрична точке A относительно прямой g.
Прямая g называется осью симметрии.
Таким образом, точки A и A1 симметричны относительно прямой g, если эта прямая проходит через середину отрезка AA1 и перпендикулярна к нему.
Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A.
Преобразование фигуры F в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.
Фигуры F и F1 называются фигурами, симметричными относительно прямой g.

Например, треугольники ABC и A1B1C1 симметричны относительно прямой g.
Если преобразование симметрии относительно прямой g переводит фигуру в себя, то такая фигура называется симметричной относительно прямой g, а прямая g называется её осью симметрии.
Симметричная фигура своей осью симметрии делится на две равные половины. Если симметричную фигуру нарисовать на бумаге, вырезать и согнуть по оси симметрии, то эти половинки совпадут.
Примеры фигур, симметричных относительно прямой.

Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно сторонам.
2) Ромб.
Ромб имеет две оси симметрии:
прямые, на которых лежат его диагонали.
3) Квадрат, как ромб и прямоугольник, имеет четыре оси симметрии: прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.
4) Окружность.
Окружность имеет бесконечное множество осей симметрии:
любая прямая, содержащая диаметр, является осью симметрии окружности.
5) Прямая.
Прямая также имеет бесконечное множество осей симметрии: любая перпендикулярная ей прямая является для данной прямой осью симметрии.
6) Равнобедренная трапеция.
Равнобедренная трапеция — фигура, симметричная относительно прямой,перпендикулярной основаниям и проходящей через их середины.
7) Равнобедренный треугольник.
Равнобедренный треугольник имеет одну ось симметрии:
прямую, проходящую через высоту (медиану, биссектрису), проведённую к основанию.

Равносторонний треугольник имеет три оси симметрии:
прямые, содержащие его высоты (медианы, биссектрисы).
9) Угол.
Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.
Теорема.
Осевая симметрия является движением.
Осевая симметрия
Цели
урока: создать
содержательные и организационные условия для развития умений строить
симметричные фигуры и находить оси симметрии в треугольниках.
Задачи
урока:
·
Образовательные: продолжить изучение понятия осевой
симметрии, показать явления симметрии в природе, архитектуре и технике, уметь
находить симметричные объекты в окружающем мире, приобретение навыков
самостоятельной работы.
·
Развивающие: развитие логического мышления, творческой
активности, познавательного интереса. Развивать умение кратко излагать свои
мысли.
Теоретическая
часть:
Что
такое симметрия? Основные понятия.
Симметрия — это соразмерность, пропорциональность
частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если
обе части от центра одинаковы, то это симметрия.
Ось
симметрии фигуры — это
прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять,
что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой
пересекаются все оси симметрии.Осевая
Осевой
симметрией называется
симметрия, проведенная относительно прямой. При осевой симметрии любой точке,
расположенной по одну сторону прямой, всегда соответствует другая точка на
второй стороне этой прямой.
При
этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
На рисунке осевая симметрия: отрезки AB
и А1В1 симметричны относительно прямой
Осевая симметрия часто встречается в повседневной жизни:
Давайте
разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1.
Постройте треугольник A1B1C1 ,симметричный
треугольнику ABC относительно прямой.
- Проведем
из вершин треугольника ABC три прямые, перпендикулярные оси симметрии,
выведем эти прямые на другую сторону оси симметрии. - Найдем
расстояние от вершин треугольника ABC до точек на оси симметрии. - С
другой стороны прямой отложим такие же расстояния. - Соединяем
точки отрезками и строим треугольник A1B1C1,
симметричный треугольнику ABC. - Получаем
два треугольника, симметричных относительно оси симметрии.
Пример
2. Постройте треугольник, симметричный треугольнику ABC относительно прямой.
- Строим
по уже известному алгоритму. Проводим прямые из вершин треугольника ABC и
выводим их на другую сторону оси симметрии. - Измеряем
расстояние от вершин до точек на прямой. - Откладываем
такие же расстояния на другой стороне оси симметрии. - Соединяем
точки и строим треугольник A1B1C1.
Пример
3. Построить отрезок A1B1, симметричный отрезку AB
относительно прямой.
- Измеряем
расстояние от точки B до прямой и от точки A до прямой. - Проводим
прямую от точки А через прямую под прямым углом к прямой, выводя за ось
симметрии. - Проводим
прямую от точки B через прямую под прямым углом к прямой, выводя за ось
симметрии. - Соединяем
точки A1 и B1 и получаем отрезок A1B1,
симметричный данному.
Задачи:
1.
Постройте фигуру, симметричную данной
относительно прямой.
2.
Постройте фигуру, симметричную данной
относительно прямой.