Ускорение силы тяжести

3.9
Средняя оценка: 3.9
Всего получено оценок: 105.
3.9
Средняя оценка: 3.9
Всего получено оценок: 105.
Процесс изменения скорости при движении физического тела характеризуется ускорением. Ускорение силы тяжести (обозначается буквой g) возникает в результате влияния силы тяжести, которая действует на любое тело у поверхности Земли или другой планеты. Разберемся от чего зависит значение g и как его определяют.
Основные формулы для равноускоренного движения
Равноускоренное движение — самый простой вид неравномерного движения. Равноускоренным называется движение с ускорением, постоянным по модулю и направлению:
$ a = {Δvover Δt} = const $ (1),
где:
Δv — изменение скорости (“дельта v “), м/с;
Δt — промежуток времени, (“дельта t “)за которое произошло изменение скорости, с.
Из формулы (1) следует, что размерность ускорения будет выражаться в метрах на секунду в квадрате:
$ {1 м/сover 1 c} = 1 м/с^2 $ (2).
Второй закон Ньютона гласит:
$ F = m * a $ (3),
где:
F — сила, действующая на тело, Н;
m — масса тела, кг;
a — ускорение, м/с2.
Сила тяжести и ускорение свободного падения
При свободном падении на Землю все тела, независимо от их массы, движутся одинаково. Свободное движение является равноускоренным движением. Ускорение, с которым падают на Землю тела в пустоте, называется ускорением свободного падения (или ускорением силы тяжести). Условие пустоты или, что тоже самое, вакуума, требуется для исключения влияния сопротивления атмосферного воздуха. Сила притяжения Fт со стороны Земли на тело массой m, называется силой тяжести:
$ F_т = m * g $ (4),
Определением ускорения силы тяжести впервые систематически занимался Галилео Галилей — итальянский математик, физик, астроном. Будучи профессором университета в городе Пиза, Галилей измерял время падения предметов с высоты местной, слегка наклонной, башни.
.
В результате этих наблюдений он пришел к следующим выводам:
- Время падения не зависит от массы тела. Все тела падают одинаково;
- Падение тел представляет собой равноускоренное движение с ускорением $ g = 9,81{ мover c^2} $ .
И хотя это открытие датировано 1589г., современное, общепринятое среднее значение g практически не отличается от этого значения. Когда от расчетов не требуется высокой точности, то принимают, что модуль g равен 10 м/с2.
Последовавшие за Галилеем более точные измерения показали, что значение g не является абсолютной константой, а зависит от местоположения измерений в разных точках Земли. Ответ на этот вопрос нашел английский ученый Исаак Ньютон.
Закон всемирного тяготения
В 1682 г. Ньютон открыл закон всемирного тяготения, из которого следует:
- все тела притягиваются друг к другу;
- сила тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними;
- векторы сил тяготения направлены вдоль прямой, соединяющей тела.
Этот закон универсален, и для случая пары тел, одно из которых является произвольным телом массой m, а второй — Земля, в виде формулы выглядит так:
$ F_т = G * {{m * Mз }over {(R_з + h)^2} } $ (5),
где:
Mз — масса Земли, кг;
Rз — радиус Земли, м;
h — высота, на которой находится тело, относительно поверхности Земли, м;
G — гравитационная постоянная, равная 6,6720 * 10-11 Н*м2 * кг-2.
Из формул (4) и (5) следует, что:
$ g = G * {{ Mз }over {(R_з + h)^2 } }$ (6)
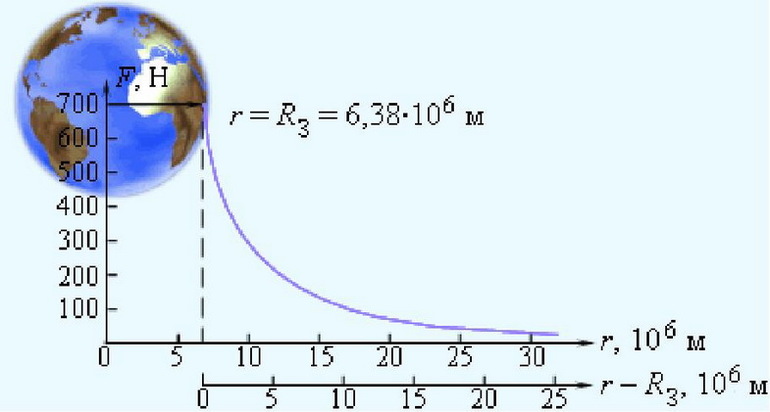
Из (6) следует, что ускорение силы тяжести будет зависеть от высоты h и величины радиуса Земли, который для обычных расчетов принимается равным примерно 6400 км. Но поскольку форма Земли не является идеальным шаром, а сплюснута к полюсам, то точные значения g будут отличаться от среднего значения в 9,81 м/с2:
- максимальное значение gмакс = 9,83 м/с2 — на полюсах Земли, где Rз меньше;
- минимальное значение gмин = 9,79 м/с2 — на экваторе Земли, где Rз больше.
Из формулы (6) также следует, что ускорение силы тяжести на других планетах, имеющих массу, отличающуюся от массы Земли, будет для космонавтов значительно отличаться от привычных земных условий. Так, например:
- На Марсе — gМарса = 3,86 м/с2;
- На Меркурии — gМеркурия = 3,7 м/с2;
- На Луне — gЛуны = 1,62 м/с2;
- На Нептуне — gНептуна = 11,0 м/с2.
Как определяют ускорение силы тяжести
Для точного измерения силы тяжести, а значит, и ускорения, используется прибор, называемый гравиметром. Прибор применяется при поиске полезных ископаемых и для сбора информации археологами, палеонтологами, гидрологами и представителями других профессий, изучающих поверхность Земли.
Следует упомянуть еще два фактора, влияющих на значение ускорения свободного падения:
- Известно, что Земля вращается вокруг своей оси, имея при этом так называемое центростремительное ускорение, которое влияет на величину ускорения свободного падения;
- Масса Земли распределена неравномерно, например, в местах расположения больших месторождений металлических руд ускорение силы тяжести будет больше, а там, где есть пустоты (газовые месторождения) ускорение будет несколько меньше.
Эти факторы дают очень малые отклонения от средних значений g , но зато их регистрация позволяет, например, геологам находить новые месторождения полезных ископаемых.
Что мы узнали?
Итак, мы узнали, что такое ускорение силы тяжести. Сила тяжести возникает вследствие действия силы гравитации, подчиняющейся закону Ньютона (формула (5)). На Земле среднее значение ускорения силы тяжести gЗемли равно 9,81 м/с2. Для точного определения ускорения силы тяжести требуется использование современных приборов, называемых гравиметрами.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Александр Коновалов
4/5
Оценка доклада
3.9
Средняя оценка: 3.9
Всего получено оценок: 105.
А какая ваша оценка?
Второй закон Ньютона это закон который был выведен в результате проведения опытов Ньютоном.
В результате чего были выведена новая формула второго закона ньютона а = F /m,
Что такое второй закон Ньютона, масса и вес тела

Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение.
Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.
Ускорение от величины силы
I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу.
Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = (at2) : 2 определим ускорение a.
Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку
a1 : a2 = F1 : F2
ИЛИ
а ~ F.
Отношение силы, действующей на тело, к ускорению есть величина постоянная, которую обозначим m. Это отношение назовем массой тела.
Зависимость ускорения от массы
II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку).
Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть
(a1/a2) = (m2/m1), или а ~ (1/m)
Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела (второй закон ньютона формулировка).
Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так (формула второго закона ньютона):
а = F /m
где а — ускорение, m—масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила.
Результирующая сила F равна векторной сумме всех сил, приложенных к телу;
F = mа.
Следовательно, сила равна произведению массы на ускорение.
Второй закон динамики можно записать в иной более удобной форме. Учитывая, что ускорение
а = (υ2 — υ1) / (t2 — t1)
подставим это выражение в уравнение второго закона Ньютона. Получим
F = ma = (mυ2 — mυ1) / (t2 — t1) = (∆(mυ))/∆t
Что такое импульс
Импульсом, или количеством движения, называется вектор, равный произведению массы тела на его скорость (тυ).
Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени (второй закон ньютона в импульсной форме)
F = (∆(mυ))/∆t
Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содержащегося в данной теле. Это определение несовершенно.
Из второго закона Ньютона вытекает следующее определение массы. Из равенства
a1/a2= m2/m1
видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость этого тела и наоборот.
Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности. Тогда можно сказать, что масса есть мера инертности тела.
Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону:
где m — масса тела, движущегося со скоростью υ; m0 — масса этого же тела, находящегося в покое; с = 3 • 108м/с скорость света в вакууме.
Проанализируем данное уравнение:
- Если υ«с, то величиной —, как очень малой, можно пренебречь и m = m0, то есть при скоростях движения, много меньших скорости света, масса тела не зависит от скорости движения;
- Если υ ≈ с, то υ2/с2 ≈ 1, тогда т = m0/0— отсюда вытекает, что m → ∞.
По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы.
Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует.
Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно.
Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях.
Масса тела с ростом скорости
Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества.
Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю.
Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже).
Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при υ0 = 0) называется свободным падением.
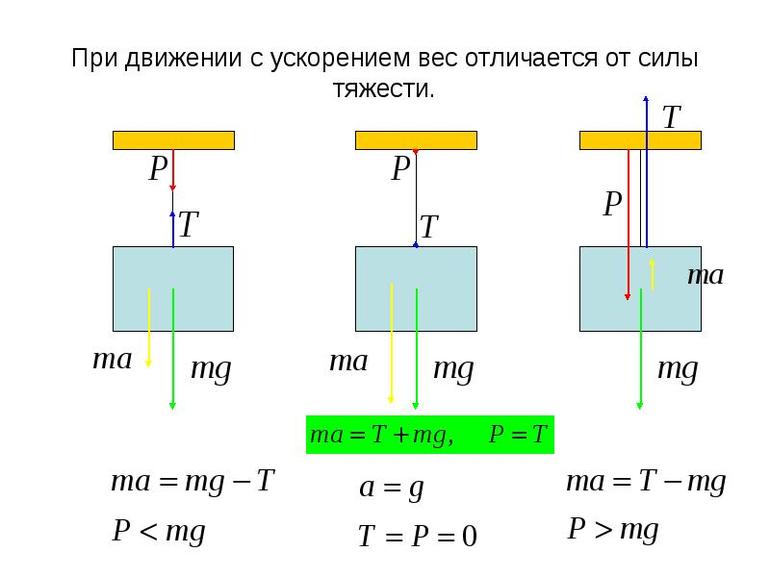
Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р.
Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес.
Если Р— сила тяжести, m — масса, g — ускорение силы тяжести (в данной точке Земли оно для всех тел одинаковой среднее его значение равно 9,8м/с2), то применяя второй закон динамики, получим
P = mg.
Выразим с помощью этой формулы веса двух различных тел. Тогда:
P1 = m1g и Р2 = m2g. Разделив почленно эти два равенства, будем иметь
P1/P2 = m1/m2
Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.
Задачи на второй закон ньютона
1. Какая сила F действует на автомобиль массой кгm=1000 кг, если он движется с ускорением мсa=1 м/с2.
Дано:
m = 1000 кг
a = 1 м/с2
Найти: F — ?
Решение:
Запишем второй закон Ньютона :
F = mа.
F = 1000 кг • 1 м/с2 = 1000 Н
Ответ: 1000 Н.
2. На мяч действует сила F = 70Н, масса мяча m = 0,2 кг, найти его ускорение a.
Дано:
m = 0,2 кг,
F = 70Н
Найти:
a — ?
Решение:
Запишем второй закон Ньютона :
F = mа.
Следовательно а = F / m.
а = 70Н : 0,2 кг = 350 м/с.
Ответ: а = 350 м/с.
Статья на тему Второй закон Ньютона
Немного истории
Человека издревле интересовали звезды и планеты, которые видимы ночью и исчезают в дневное время суток. Люди пытались понять, в каком мире они живут, каким законам подчиняются наблюдаемые процессы движения и перемещения.
С приходом Нового времени в Европе начинается расцвет научной мысли. На первый план в научном мире выходят такие личности, как Коперник, Галилей, Кеплер, Ньютон. Все они внесли огромный вклад в изучение явления гравитации.
Коперник впервые оформил теорию гелиоцентрического мира, Галилей издал несколько трудов по изучению явления свободного падения и вычислению ускорения силы тяжести, Кеплер собрал эмпирическую информацию о законах движения планет и вывел законы, носящие его фамилию. Что касается Ньютона, то он впервые смог объединить все знания человечества о правилах перемещения тел и оформить их в виде красивого универсального закона всемирного тяготения.
После Ньютона уже в XX веке Альберт Эйнштейн предложил собственное объяснение явлению тяготения, которое он выразил в виде общей теории относительности.
Классическая и эйнштейновская гравитация в настоящее время являются двумя столпами, на которые опираются ученые с целью создания теории всего.
Классическая теория тяготения
Исаак Ньютон в XVII веке смог доказать в своих научных работах, что падение тел на земле и движение небесных объектов подчиняется одним и тем же законам. Ключевой силой во всех этих случаях является гравитация или тяготение. После обобщения имеющихся эмпирических данных многих лет наблюдений за космическими телами английский ученый вывел формулу силы тяжести. Она записывается в следующем виде:
F = G*M1*M2/R 2.
Здесь M1 и M2 — это массы двух взаимодействующих тел, R — расстояние между их центрами, G — универсальная гравитационная постоянная, которая приблизительно равна 6,67*10^(-11) Н*м 2 /кг 2. Буквы размерности постоянной G легко понять, если вспомнить, что сила вычисляется в ньютонах (Н) в международной системе СИ.
Чтобы понять физический смысл ускорения падения, следует подробнее рассмотреть величину F. Из записанной формулы силы тяжести в физике можно сделать следующие выводы о ее характере и свойствах:
- Она всегда является притягивающей и действует между телами, которые имеют конечные (ненулевые) массы. Подобный характер и возникновение силы F подтверждается тем, что орбиты многих космических тел имеют замкнутую форму (эллиптическая), что невозможно в случае отталкивающей гравитации.
- Бесконечность действия. На каком бы огромном расстоянии ни находились два тела M1 и M2, они будут испытывать притяжение друг к другу, и формула для F всегда будет давать ненулевой результат.
- Центральность. Здесь речь идет о направленности вектора силы от центра масс одного объекта к центру масс другого.
- Сила F уменьшается с увеличением дистанции между телами, причем скорость ее убыли описывается квадратным законом. Увеличение расстояния в 2 раза приводит к уменьшению F в 4 раза.
Понятие об ускорении
В начале XVII века итальянский философ Галилео Галилей, проводя свои опыты с брошенными вниз предметами, выяснил, что если пренебречь силой сопротивления воздуха, то они достигают поверхности земли за одно и то же время. При этом во время падения скорость предметов увеличивается по линейному закону.
Несколькими десятилетиями позже Исаак Ньютон постулировал свой знаменитый второй закон. Он устанавливает следующую взаимосвязь между действующей на тело силой F, его массой m и ускорением a:
F = m*a.
Ускорение является результатом действия силы на объект конечной массы. Сама величина a имеет следующий физический смысл: она показывает, на какую величину и в какую сторону изменяется модуль скорости за единицу времени. Ее размерность обозначается м/с 2. Например, a = — 3 м/с 2, это означает, что скорость тела v за каждую секунду уменьшается на 3 м/с.
Развитие кинематики позволило установить следующие математические взаимодействия между величинами a, v, s (здесь s — пройденный телом путь):
v = v0+/- a*t;
s = v0*t +/- a*t 2 /2.
Где v0 — определение начальной скорости. Кратко можно сказать, что ускорение — это физическая величина, которая определяет однозначно скорость изменения самой скорости. Найти его можно через производную v по времени t.
Падение под действием тяжести
Каждый замечал, что брошенный вверх камень неминуемо возвращается на землю. Происходит это потому, что на него, как и на любой другой предмет, действует земная гравитация. С применением второго ньютоновского закона можно определить следующее равенство:
F = m*g.
Здесь произведение массы тела m на ускорение свободного падения g равно силе тяжести F. Последняя величина вблизи поверхности нашей планеты по модулю равна 9,81 м/с 2. Если бросить вниз тело, то за каждую секунду падения оно будет увеличивать свою скорость почти на 10 м/с, то есть на 36 км/ч. В реальности такого не происходит, потому что с увеличением v сильное влияние на движение начинает оказывать сопротивление воздуха.
Полезно разобраться с вопросами, откуда в физике появилась величина g и почему она имеет значение 9,81 м/с 2 вблизи поверхности Земли. Для этого следует записать заново закон Всемирного тяготения и сравнить его со вторым ньютоновским постулатом:
F = G*M1*m/R 2;
F = m*g.
Из этих выражений следует лаконичное равенство:
g = G*M1/R 2.
Подставив в него массу нашей планеты M1 и среднее значение ее радиуса, можно получить численный результат 9,81 м/с 2. Также эта формула показывает, что на разных планетах, астероидах и звездах значение g будет существенно различаться.
Вес в физике
Записанная формула для F тождественна выражению для веса P тела. Он также измеряется в ньютонах, хотя многие люди часто путают его с массой, единицей измерения которой являются килограммы.
Вес P — это величина, с которой предмет давит на опору. Причиной его появления является вся та же сила тяготения.
В отличие от массы, величина P не является характеристикой тела и изменяется в зависимости от внешних условий.
Здесь полезно привести два примера:
- Когда космонавт взлетает на ракете или гонщик Формулы-1 начинает движение, то его вес увеличивается в десять и более раз. В таких случаях говорят о перегрузках.
- Находящиеся на орбитальной станции космонавты испытывают состояние невесомости. Происходит это потому, что центробежное ускорение оказывается равным величине g на высоте траектории станции.
Земной геоид
Не только от массы тел, но также от их формы зависит значение ускорения свободного падения. Объясняется это тем, что находящиеся на поверхности массивных объектов предметы расположены на разной дистанции от их массового центра. Ярким примером является наша Земля. Ее форма представляет собой шар, сплюснутый слегка с полюсов. Называется такая фигура геоидом.
Форма геоида приводит к тому, что расстояние от полюсов до центра планеты составляет 6356,8 км, а от экватора оно будет равно 6378,1 км, то есть на 21 км больше. Учитывая, что масса планеты составляет 5,9736*10 24 кг, можно рассчитать разницу между экваториальным ge и полярным gp ускорениями свободного падения. Чтобы ее узнать, следует подставить числа в формулу:
ge = 6,67*10^(-11)*5,9736*10 24 /(6378100)^2 = 9,79 м/с 2;
gp = 6,67*10^(-11)*5,9736*10 24 /(6356800)^2 = 9,86 м/с 2.
Относительно экваториальной величины полярная больше на 0,7%. Иными словами, вес тел на полюсах будет несколько больше, чем в экваториальных широтах. Разница для человека с массой тела 70 кг составит почти 0,5 кг.
Планета Юпитер
Это самая крупная по массе и диаметру планета Солнечной системы, которая относится к группе газовых гигантов.
Ее поверхность, по мнению ученых, представляет собой жидкую основу, а атмосфера состоит из густых облаков метана, аммиака и некоторых других газов. Если человеку удалось попасть на Юпитер, то он бы испытывал огромные трудности по перемещению собственного тела. Связано это с большим по сравнению с земным ускорением g на поверхности гиганта. Чтобы его рассчитать, следует воспользоваться уже известной формулой для g:
g = G*M1/R 2.
Подставляя M1 = 1,899*10 27 кг, R = 71 492 км, можно вычислить g. Газовый гигант способен сообщать телам ускорение 24,78 м/с 2. Это означает, что человек массой 70 кг на поверхности Юпитера будет ощущать себя в 2,5 раза тяжелее, будто бы его тело имеет 170−180 кг.
Баллистические расчеты траекторий
Знание закона Ньютона, а также набора формул кинематики можно использовать для расчета траекторий любых летящих тел без дополнительной поддержки, например, брошенного мяча или выстрелянного снаряда. Подобными расчетами занимается специальный прикладной раздел физики — баллистика.
Результаты простых баллистических расчетов опираются на следующие приближения:
- пренебрежение кривизной земной поверхности;
- постоянство величины g, что справедливо для небольших высот;
- отсутствие учета силы трения воздуха;
- пренебрежение силой Кориолиса, которая связана с вращением Земли вокруг собственной оси.
Для получения достоверных результатов расчетов в случае межконтинентальных ракет, движущихся с большими скоростями, необходимо учитывать все эти приближения.
Ускорение свободного падения характеризует то, как быстро будет увеличиваться скорость тела при свободном падении. Свободным падением называется ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести. Из физики известно, что ускорение свободного падения на Земле составляет (9,8)
мс2
.
Вопрос, почему эта величина именно такая, мы рассмотрим в этой теме.
Ускорение свободного падения в упрощённом виде можно рассчитать по формуле
g=Fm
, которая получается из формулы
F=m⋅g
, где (F) — сила тяжести либо вес тела в состоянии покоя или равномерного прямолинейного движения, (m) — масса тела, которое притягивает планета, (g) — ускорение свободного падения.
Сила тяжести, действующая на тело, зависит от массы тела, массы планеты, притягивающей тело, и от расстояния, на котором находится тело от центра массы планеты.
(F) — сила тяжести, Н;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
(R) — расстояние между центрами планеты и объекта в метрах. Если притягиваемое тело находится на поверхности планеты, тогда (R) равен радиусу планеты (если планета имеет сферическую форму);
m1 и
m2
— масса планеты и притягиваемого тела, выраженные в кг.
Обрати внимание!
Если мы объединим обе формулы, тогда получим формулу
g=G⋅mR2
, с помощью которой можно вычислить ускорение свободного падения на любом космическом объекте — на планете или звезде.
Пример:
ускорение свободного падения у поверхности Земли вычисляют таким образом:
, где
(g) — ускорение свободного падения;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
Практически на Земле ускорение свободного падения на полюсах немного больше ((9,832)
мс2
), чем на экваторе ((9,78)
мс2
), так как Земля не имеет форму идеального шара, а на экваторе скорость вращения больше, чем на полюсах. Среднее значение ускорения свободного падения у поверхности Земли равно (9,8)
мс2
.
Ускорение свободного падения у поверхности любого космического тела — на планете или звезде — зависит от массы этого тела и квадрата его радиуса. Таким образом, чем больше масса звезды и чем меньше её размеры, тем больше значение ускорения свободного падения у её поверхности.
При помощи формулы расчёта ускорения свободного падения и измерений, проведённых для удалённых объектов, учёные-физики могут определить величину ускорения свободного падения на любой планете или звезде.
Рис. (1). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун; и карликовые планеты: Церера, Плутон, Эрида ((2003) UB (313))
Таблица (1). Ускорение свободного падения и другие характеристики планет Солнечной системы и карликовых планет
|
Небесное тело |
Ускорение свободного падения, мс2 |
Диаметр, км |
Расстояние до Солнца, миллионы км |
Масса, кг |
Соотношение с массой Земли |
|
Меркурий |
(3,7) |
(4878) |
(58) |
(3,3*) 1023 |
(0,055) |
|
Венера |
(8,87) |
(12103) |
(108) |
(4,9*) 1024 |
(0,82) |
|
Земля |
(9,8) |
(12756,28) |
(150) |
(6,0*) 1024 |
(1) |
|
Марс |
(3,7) |
(6794) |
(228) |
(6,4*) 1023 |
(0,11) |
|
Юпитер |
(24,8) |
(142984) |
(778) |
(1,9*) 1027 |
(317,8) |
|
Сатурн |
(10,4) |
(120536) |
(1427) |
(5,7*) 1026 |
(95,0) |
|
Уран |
(8,87) |
(51118) |
(2871) |
(8,7*) 1025 |
(14,4) |
|
Нептун |
(10,15) |
(49532) |
(4498) |
(1,02*) 1026 |
(17,1) |
|
Плутон |
(0,66) |
(2390) |
(5906) |
(1,3*) 1022 |
(0,0022) |
|
Луна |
(1,62) |
(3473,8) |
(0,3844 ) (до Земли) |
(7,35*) 1022 |
(0,0123) |
|
Солнце |
(274,0) |
(1391000) |
— |
(2,0*) 1030 |
(332900) |
Нейтронные звёзды имеют малый диаметр — порядка десятков километров, — а масса их сопоставима с массой Солнца. Поэтому гравитационное поле у них очень сильное.
Пример:
если диаметр нейтронной звезды равен (20) км, а масса её в (1,4) раза больше массы Солнца, тогда ускорение свободного падения будет в (200000000000) раз больше, чем у поверхности Земли.
Его величина приблизительно равна
2⋅1012 мс2
. Значение ускорения свободного падения для нейтронной звезды может достигать значения
7⋅1012 мс2
.
Um=120 B
T=0.08 c
v=1/T=12.5 Гц
Uд=Um/√2=120/√2≈85 B
==================
Т. к. резисторы соединены последовательно, значит, общее сопротивление R = R1 + R2 = 9 Ом
Напряжение равно силе тока, умноженной на сопротивление
U = R * I = 9 Ом * 1,6 А = 14,4 В
Во втором резисторе выделится в 2 раза больше теплоты, чем в первом, т. к. сопротивление в 2 раза больше
Відповідь:
787.4кг/м^3
Пояснення:
V=127 л=127дм^3=0.127м^3
ρ=m/V=100/0.127=787.4кг/м^3
A=UIt; A=380B*25A*20c=190000Дж=190кДж
340*6=2040. Т.е. 2 м 40 см= длина стены