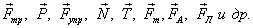Мы уже познакомились с силами упругости и трения качественно, теперь рассмотрим их количественно, с привлечением формул.
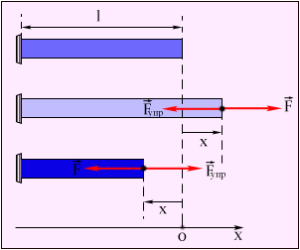
Сила упругости возникает в любом теле, если менять его форму и/или размеры. Например, сжимая пластилин или глину, мы чувствуем их противодействие – это сила упругости. Она не зависит от того, насколько пластилин или глина уже сжаты. Иное дело, если мы возьмём резиновый шарик либо стальную пружину. Чем больше мы будем их сжимать или растягивать, тем большая сила упругости будет возникать (см. рисунок).
Продолжим опыт с гирями и динамометром, рассмотренный в предыдущем параграфе. С помощью линейки будем измерять удлинение пружины Δl, равное разности её конечной и начальной длины: l – l0. Мы обнаружим, что возникающая сила упругости прямо пропорциональна модулю изменения длины пружины:
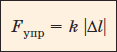 |
Fупр – сила упругости пружины, Н |Δl| – модуль удлинения пружины, м k – коэффициент жёсткости, Н/м |
Коэффициент k характеризует жёсткость пружины. Поясним его смысл. Пусть, например, мы растянули пружину динамометра на 5 см, и в ней возникла сила упругости 2 Н. Тогда жёсткость этой пружины равна: k = 2 Н : 0,05 м = 40 Н/м. Допустим теперь, что мы взяли пружину из более толстой проволки. Приложив к ней такую же силу 2 Н, мы заметим меньшее растяжение, например 1 см. Тогда жёсткость такой пружины будет больше: k = 2 Н : 0,01 м = 200 Н/м.
Более углублённо мы рассмотрим силу упругости в 9 классе.
Как вы уже знаете (см. § 3-б), сила трения бывает двух видов – трения скольжения и трения покоя. При участии жидкостей или газов сила трения покоя всегда равна нулю, а вместо термина «сила трения скольжения» чаще употребляют термин «сила сопротивления движению». Формулы, описывающие трение с участием жидкостей и газов, сложны, поэтому мы рассмотрим только формулу для силы трения скольжения твёрдого тела по поверхности другого твёрдого тела.
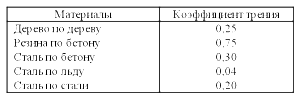
Проделаем опыт. Деревянный брусок весом 2 Н будем равномерно тянуть по горизонтальной доске, измеряя силу трения. Сверху на брусок будем ставить грузики по 1 Н, увеличивающие вес бруска. Результаты опыта занесём в таблицу:
| Количество грузиков, шт. | – | 1 | 2 | 3 |
| Вес бруска с грузиками | 2 Н | 3 Н | 4 Н | 5 Н |
| Сила трения скольжения | 0,6 Н | 0,9 Н | 1,2 Н | 1,5 Н |
Из сравнения нижних пар значений двух сил видно, что возникающая сила трения скольжения пропорциональна силе давления на опору (в нашем случае – действующему на доску весу бруска и грузиков). Эта закономерность выражается формулой:
 |
Fтр – сила трения скольжения, Н N – сила давления на опору, Н μ – коэффициент сухого трения |
Взяв любую пару значений сил, мы подсчитаем коэффициент трения скольжения деревянного бруска по деревянной доске в нашем опыте. Например, μ = 0,6 Н : 2 Н = 0,9 Н : 3 Н = 1,2 Н : 4 Н = 1,5 Н : 5 Н = 0,3. То есть μ = 0,3. Этот коэффициент показывает, что сила трения скольжения в нашем опыте составляет 3/10 от силы давления на опору.
Случаи негоризонтальных поверхностей мы рассмотрим в 9 классе.
-
Деформация тела.
-
Упругие и
пластические дформации. -
Сила упругости.
-
Абсолютная и
относительная деформации. Механическое
напряжение. -
Закон Гука, модуль
Юнга (модуль упругости). -
Потенциальная
энергия деформированного тела. -
Коэффициент
жёсткости системы параллельных пружин. -
Коэффициент
жёсткости системы последовательно
соединённых пружин. -
Сила трения.
-
Сухое трение.
-
Трение скольжения.
-
Трение качения.
-
Трение покоя.
-
Законы трения.
-
Коэффициент
трения. -
Вязкое (жидкое)
трение.
1. Деформация
тела –
изменение формы и размеров тела вследствие
относительного смещения различных
его частей, происходящего под действием
внешних сил.
2.
Упругие и пластические деформации.
Если после снятия нагрузки тело принимает
прежнюю форму и размеры, то деформация
называется упругой.. Если же после снятия
нагрузки тело остается деформированным,
то такая деформация называется
пластической. Соответственно различают
тела упругие и пластичные. Однако не
существует тел абсолютно пластичных
или абсолютно упругих. Даже очень упругое
тело при больших деформациях после
снятия нагрузки может остаться заметно
деформированным. Аналогично мягкое,
пластичное тело при очень малых
деформациях будет проявлять упругие
свойства. Например, если стальную пружину
сильно растянуть, то после снятия
нагрузки она не примет прежнюю длину.
Также и пружина изготовленная и свинцовой
проволоки при очень малых деформациях
проявляет упругие свойства.
3.Сила
упругости
– сила, возникающая при деформации тела
и направленная против смещения частей
тела при деформации. Сила упругости
стремится восстановить размеры и форму
тела.
Атомы состоят из
положительно и отрицательно заряженных
частиц, поэтому между ними действуют
электромагнитные силы притяжения и
отталкивания, которые удерживают атомы
на средних расстояниях друг от друга,
соответствующих состоянию равновесия.
При растяжении
тела расстояния между атомами
увеличиваются, и силы притяжения
преобладают над силами отталкивания.
Если же тело сжимают, то расстояния
между атомами уменьшаются, и силы
отталкивания преобладают над силами
притяжения. Таким образом сила по своей
природе есть сила электромагнитная.
4.Абсолютная
и относительная деформации, механическое
напряжение.
Пусть тело цилиндрической формы одним
концом закреплено неподвижно, а другой
его конец остаётся свободным. Пусть
площадь поперечного сечения цилиндра
– S,
а
—
его первоначальная длина, т.е. длина
цилиндра в ненапряженном состоянии
(Рис. 35). К свободному концу приложим
силу F
, которая
стремится растянуть тело. При этом его
длина увеличится и станет равной l
, тогда
есть абсолютное удлинение причем
.
Если же сила стремится сжать тело, то
его длина уменьшается и
В дальнейшем будем пользоваться модулем
абсолютного удлинения или модулем
смещения
.
Безразмерную величину
называют относительной
деформацией или относительным удлинением.
Отношение силы F
к площади сечения S
называют механическим
напряжением или нагрузкой. В системе
СИ напряжение измеряется в
,
т.е. как и давление в паскалях.
5.Закон
Гука. Модуль
Юнга. В 1675
г. английский физик Роберт Гук
обнаружил, что напряжение, возникающее
в деформируемом теле, пропорционально
относительной деформации. Эта зависимость
выражается формулой
и называется
законом Гука. Коэффициент Е
имеет
размерность
,
определяется свойствами данного
материала и называется модулем Юнга (
модуль упругости). Его
физический смысл
заключается
в том, что он численно равен напряжению
возникающему при относительной
деформации
равной единице (
),
но это значит что абсолютная деформация
равна
первоначальной
длине тела, что практически невозможно.
Подставляя в последнее равенство
и
получим закон Гука в виде:
,
где
— коэффициент жесткости тела, измеряемый
в
и зависящий от формы, размеров тела и
свойств материала. Далее обозначим
.
Теперь закон Гука запишем в виде
.
По третьему закону
Ньютона модуль внешней силы, вызывающей
деформацию тела, равен модулю силы
упругости, возникающей при его деформации,
т.е.
,
поэтому
И так, закон Гука
гласит:
“Модуль
силы
упругости, возникающей при деформации
тела
пропорционален
модулю его удлинения”
Сила упругости
направлена против смещения деформации
поэтому часто закон Гука записывают в
виде
.
Закон Гука
справедлив лишь при достаточно малых
деформациях когда
.
В этом случае деформация называется
упругой, т. е. после снятия нагрузки тело
принимает первоначальную форму и размер.
Если же деформация
окажется значительной, то пропорциональная
зависимость силы упругости от удлинения
будет нарушена (закон Гука не выполняется).
В этом случае после снятия нагрузки
тело остаётся деформированным. Такие
деформации называются пластическими.
Не существует
деления тел на абсолютно упругие и
абсолютно пластические, т. к. при
определённых деформациях каждое тело
проявит либо пластичность, либо упругость.
6.Потенциальная
энергия деформированного тела.
По закону сохранения энергии, работа
внешних сил при упругих деформациях
превращается в потенциальную энергию
деформированного тела. Эту работу
вычислим с помощью графика зависимости
деформации тела от действующей силы,
который в пределах применимости закона
Гука есть прямая линия (Рис. 36). Пусть
тело получило удлинение
,
при этом модуль деформирующей силы по
закону Гука равен
.
Продолжим удлинение тела на очень малую
величину
в пределах сил можно приближенно считать
постоянной и равной
.
Тогда работу по растяжению тела от
до
вычислим по формуле
или
.
На Рис.36 эта работа равна площади
заштрихованного прямоугольника с
сторонами
и
.
Переходя последовательно от одного
состояния к состоянию бесконечно
близкому и суммируя площади всех
прямоугольников получим работу
деформирующей силы при удлинении от 0
до l
, которая и будет равна площади
прямоугольного треугольника АВС с
катетами ОС=l
и СВ=F(l)=kl.
Итак,
потенциальная энергия деформированного
тела выражается формулой
.
7.
Коэффициент
жесткости системы параллельных пружин.
Пусть две пружины с коэффициентами
жесткости
и
соединены параллельно как показано на
Рис.37 и пусть планка АВ, к которой они
присоединены, под действием силы F
перемещается поступательно, т.е.
удлинения пружин одинаковы и равны х
. По третьему закону Ньютона
,
где
силы упругости пружин. Заменим систему
двух пружин одной эквивалентной им
пружиной с коэффициентом жесткости к
такой, что
,
тогда
,
сокращая на х
получим коэффициент жесткости системы
двух параллельных пружин:
.
Для системы n
параллельных пружин коэффициент
жесткости равен сумме
.
8
.Кэффициент
жесткости системы последовательно
соединенных пружин.
Пусть две пружины с коэффициентами
жесткости
и
соединены последовательно (Рис.38) под
действием силы
F
пружины
получают удлинения
и
,
полное удлинение пружин системы равно
сумме
.
Согласно третьему
Ньютона
,
где
,
—
силы упругости, возникающие в пружинах.
Заменим эту систему
пружин одной им эквивалентной пружиной
с коэффициентом жесткости k
таким, что под действием силы F
она получает удлинение
,
т. е.
.
Подставляя сюда
и
приходим к равенству
.
Сокращая последнее
равенство на F,
получим
.
Проводя далее
элементарные алгебраические преобразования,
получим формулу для вычисления
коэффициента жесткости системы двух
последовательно соединенных пружин:
.
Аналогично для
системы n
последовательно соединенных пружин
получим:
Из
последнего равенства следует, что чем
больше число пружин, соединенных
последовательно, тем меньше коэффициент
жесткости всей системы. Причем коэффициент
жесткости системы меньше наименьшего
коэффициента жесткости пружины, входящей
в состав системы.
Рассмотрим систему
пружин с коэффициентами жесткости
и
,
изображенную на Рис.39. Силы трения
отсутствуют, и тело массы m
свободно перемещается по горизонтальной
плоскости.
Когда тело m
находится в положении равновесия,
пружины не напряжены. Если тело m
сместить на расстояние x
от положения равновесия вправо, то
пружина
удлинится, а пружина
сократится на x.
При этом силы упругости пружин будут
направлены влево и равны
и
,
а их равнодействующая —
.
Заменим эту систему пружин одной им
эквивалентной — с коэффициентом жесткости
k
таким, что
,
тогда получим равенство
из которого получим
коэффициент жесткости рассматриваемой
системы пружин
.
9. Сила
трения – сила
возникающая, при соприкосновении двух,
препядствующая их относительному
перемещению и направленная касательно
к соприкасающимся поверхностям против
перемещения. Сила трения численно равна
силе, которую нужно приложить к телу,
чтобы вызвать его перемещение по
поверхности другого тела. 10. Сухое
трение – трение при сухих поверхностях
твёрдых тел. Различают три вида сухого
трения:
а) трение покоя,
возникающее в случае, когда одно тело
покоится на поверхности другого тела,
б) трение скольжения
– трение, возникающее при скольжении
одного тела по поверхности другого
тела,
в) трение качения
– трение, возникающее, когда цилиндр
или шар катится по поверхности другого
тела.
11. Трение
скольжения обусловлено
неровностями соприкасающихся поверхностей
– макрошероховатостями и микрошероховатостями.
Макрошероховатости – это выступы и
впадины соприкасающихся поверхностей,
которые есть всегда, т. к. невозможно
создать идеально гладкую поверхность.
При движении эти
выступы соударяются, деформируются и
ломаются, вещество трущихся поверхностей
или, как говорят, диспергируется. Это
значит, что при движении приходится
преодолевать силы притяжения между
атомами и молекулами, т.е. силы
электромагнитные.
Микрошероховатости
возникают благодаря тепловому движению
атомов и молекул, т.е. неровности, которые
соизмеримы по величине с размерами
молекул. Поэтому скольжение сопровождается
отрывом отдельных молекул и их перемещением
– молекулярным диспергированием. Здесь
также преодолеваются силы электромагнитные.
Итак, сила трения
скольжения по природе своей есть сила
электромагнитная.
12.Трение
качения
обусловленодеформацией соприкасающихся
поверхностей, Поэтому шару или цилиндру,
которые катятся по поверхности другого
тела приходится как бы наезжать на
выступ в точке В
(Рис. 40) и деформировать этот выступ,
т.е. преодолевать силы упругости – силы
электромагнитные.
13.Трение
покоя
возникает при относительном покое
соприкасающихся поверхностей и
обусловлено шероховатостью поверхностей
и следовательно является силой
электромагнитной. Сила трения покоя
численно равна силе, которую нужно
приложить к телу, чтобы сдвинуть его с
места.
14. Законы
трения были
установлены экспериментально французскими
физиками Амонтоном в 1769г. и независимо
от него Кулоном в 1785г. По закону Амонтона
– Кулона сила трения пропорциональна
силе с, которой два тела прижимаются
друг к другу, т. е. силе реакции опоры:
.
Здесь
— коэффициент пропорциональности,
называемый коэффициентом трения. В
зависимости от вида сухого трения это
может быть коэффициент трения покоя,
коэффициент трения скольжения или
коэффициент трения качения. Коэффициенты
трения для различных материалов
определяют экспериментально.
1
5.Коэффициент
трения
скольжения показывает, какую часть от
реакции опоры составляет сила трения:
.
Отсюда следует,
что коэффициент трения величина
безразмерная.
Экспериментально
установлено, что наибольшим является
коэффициент трения покоя. Коэффициент
трения скольжения значительно меньше.
Это проявляется когда мы пытаемся
сдвинуть с места какой –либо предмет,
прилагаем большую силу и как только
предмет начинает скользить мы чувствуем,
что нам приходится прилагать значительно
меньшую силу, чтобы тело продолжало
скользить.
График зависимости
коэффициента трения скольжения
представлен на Рис.41. В состоянии покоя
коэффициент трения
максимален. Когда тело начинает двигаться
с малой скоростью, коэффициент трения
остаётся неизменным с ростом скорости
он уменьшается и при дальнейшем росте
скорости коэффициент трения скольжения
увеличивается, Коэффициент трения
качения является наименьшим из трёх
видов сухого трения.
16. Вязкое
трение (жидкое трение)
возникает при движении тела в жидкости
или в газе. Тонкий слой жидкости или
газа прилипает к телу благодаря притяжению
молекул вязкой среды и твёрдого тела и
движется вместе с телом. Поэтому трение
возникает между слоями вязкой среды и
оно значительно меньше сухого трения.
Главным отличием вязкого трения от
сухого трения является тот факт, что в
вязкой среде отсутствует трение покоя.
Поэтому даже большой корабль можно
сдвинуть с места малой силой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
I. Механика
Тестирование онлайн
Что надо знать о силе
Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как 
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
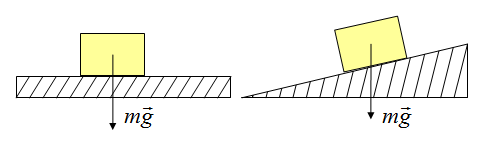
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле

Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
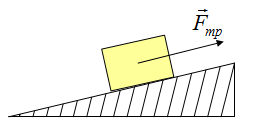
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:

Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
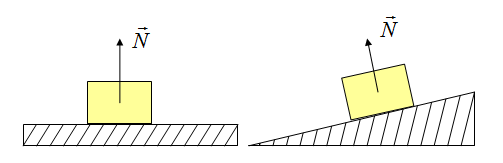
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой 

Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Закон Гука

Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.
Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
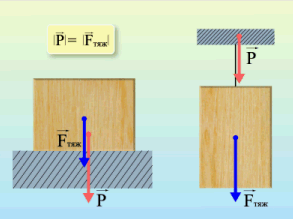
Вес тела
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
Формулы определения веса нет. Обозначается эта силы буквой 
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!
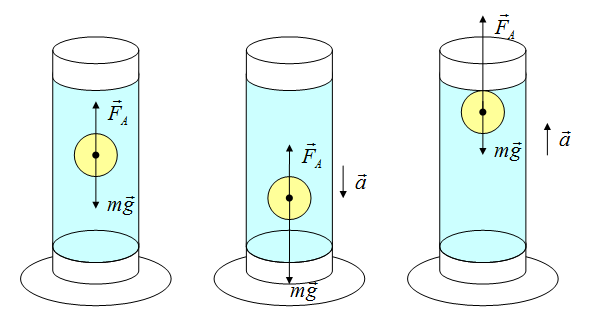
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка — отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
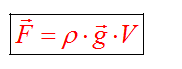
В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Силы трения*
Взаимосвязь силы тяжести, закона гравитации и ускорения свободного падения*
Особенности сил трения:
- возникают при соприкосновении двух движущихся тел;
- действуют параллельно поверхности соприкосновения тел;
- направлены против движения тела.
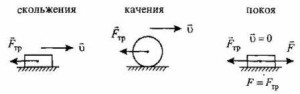
Виды силы трения:
При скольжении сила трения скольжения зависит не только от состояния трущихся поверхностей, но и от относительной скорости движения тел.
Замечено, что тяжелый предмет, например ящик, трудно сдвинуть с места, а потом двигать его становится легче. Это и объясняется уменьшением силы трения при появлении скольжения с малой скоростью. При слишком больших относительных скоростях сила трения скольжения приблизительно равна максимальной силе трения покоя:
Fтр ≈ Fтр.макс = N.
Максимальное Fтр.макс значение модуля силы трения покоя пропорционально модулю силы нормальной реакции опоры.(Этот закон впервые установил экспериментально фр. физик Кулон).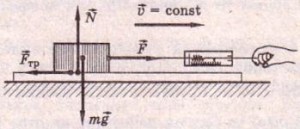
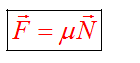
(греческая буква, читается «мю») – коэффициент пропорциональности, называемый коэффициентом трения. Он характеризует обе трущиеся поверхности и зависит не только от материала этих поверхностей, но и от качества их обработки. Коэффициент трения не имеет размерность, определяется экспериментально.
Эти значения коэффициента трения относятся к случаю, когда поверхности тел не смазаны. Смазка (минеральное масло) существенно уменьшает силу трения .
Сила упругости. 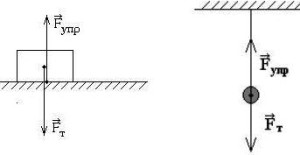
Деформация — изменение формы и объема тела под действием внешних сил. Вида деформации: растяжение, сжатие, кручение, изгиб, сдвиг.
Природа сил упругости — атомы в твердом теле расположены таким образом, что силы отталкивания одноименных электрических зарядов и силы притяжения разноименных — уравновешивают друг друга. Силы упругости по своей природе являются электромагнитными силами. В результате деформации электрические силы стремятся возвратить атомы в первоначальное состояние.
Сила упругости всегда определяется по закону Гука: При упругой деформации растяжения (или сжатия) удлинение тела прямо пропорционально приложенной силе. 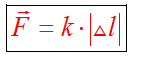
Учитывая, что проекция силы упругости деформированного тела на ось X и координата x имеют противоположные знаки, то можно записать:
Закон Гука хорошо выполняется только при упругих деформациях, при которых x мало.
На рисунке представлены деформация растяжения (x > 0) и сжатия (x < 0). Внешняя сила