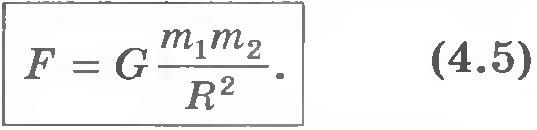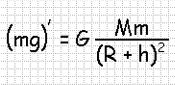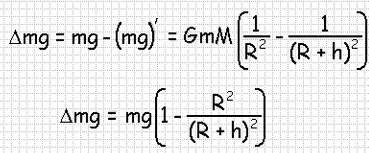Как найти силу тяготения между шарами

Гравитационные силы. Закон всемирного тяготения

Все тела в природе взаимно притягиваются друг к другу. Впервые Ньютон доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же — это сила всемирного тяготения (гравитационная сила), действующая между любыми телами Вселенной.

Гравитационные силы — это силы центральные, т. е. они направлены вдоль прямой, соединяющей взаимодействующие материальные точки.

Гравитационное взаимодействие осуществляется посредством гравитационного поля. Это поле, наряду с другими полями и веществом, является одной из форм материи.

С каждым телом неразрывно связано гравитационное поле, проявляющееся в том, что на помещенную в поле материальную точку действует гравитационная сила, пропорциональная массе этой точки.

Тело, гравитационное поле которого исследуется, называется источником поля.

Гравитационные силы зависят от положения тел (координат) (рис. 1). Их просто рассчитать для материальных точек по закону всемирного тяготения: две материальные точки притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

(~F = G frac{m_1 m_2}{r^2}) — закон всемирного тяготения.

G = 6,67·10^-11 Η·м²/кг² — гравитационная постоянная.

Гравитационная постоянная определена опытным путем. Она численно равна силе, с которой притягиваются два тела массами 1 кг, находящиеся на расстоянии 1 м друг от друга.

По закону всемирного тяготения можно рассчитать также силу притяжения между двумя сферическими телами (r — это расстояние между центрами сфер) или телами, одно из которых — шар большого радиуса, а второе — произвольной формы, но небольших размеров (рис. 2, а, б).

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 38-39.

Закон всемирного тяготения, сила тяжести

Закон всемирного тяготения, сила тяжести

Основные понятия для силы тяжести и закона всемирного тяготения

Исследуя нормальное ускорение, которое возникает при движении Луны вокруг Земли, И. Ньютон пришел к выводу о том, что все тела в природе притягиваются друг к другу с некоторой силой, названной силой тяготения. При этом ускорение, которое вызывается действием данной силы обратно пропорционально квадрату расстояния между рассматриваемыми, воздействующими друг на друга телами.

Допустим, что два точечных тела, имеющих массы $m_1 и m_2$ находятся на расстоянии $r$ друг от друга. Эти тела взаимодействуют с силами:

[F_1=m_1a_1 и F_2=m_2a_2left(1right).]

В соответствии с третьим законом Ньютона, модули сил равны:

[F_1=F_2left(2right).]

Из сказанного выше об ускорении и на основании (2) получим:

[frac{m_1K_1}{r^2}=frac{m_2K_2}{r^2}left(3right).]

Формула (3) будет справедлива, если $K_1$=$gamma m_2$, а $K_2$=$gamma m_1$, где $gamma $ некоторая постоянная. Тогда:

[F=m_1a_1=frac{m_1K_1}{r^2}=gamma frac{m_1m_2}{r^2},]

где $gamma =6,67cdot {10}^{-11}frac{Нcdot м^2}{{кг}^2}$ — гравитационная постоянная.

Формулировка закона всемирного тяготения

Строго говоря, формулу (4) можно использовать для вычисления силы тяготения между однородным шарами с массами $m_1{ и m}_2$, считая, что $r$ расстояние между центрами шаров.

Для того чтобы найти силы тяготения, которые действуют на одно тело со стороны другого тела, при этом тела точечными считать нельзя, поступают следующим образом. Оба тела теоретически делят на элементы, которые можно приять за точечные массы. Находят силы тяготения, которые действуют на один выбранный элемент первого тела со стороны всех элементов другого тела, получают силу, которая действует на рассматриваемую точку первого тела. Далее операцию повторяют для каждой точки первого тела. Полученные силы складывают с учетом их направлений. В результате получается сила тяготения, с которой второе тело действует на первое. Такая задача является весьма сложной.

Сила тяжести

Сила тяжести направлена к Центру Земли. В задачах, если размер Земли много больше, чем рассматриваемые тела, считают, что сила
тяжести направлена вертикально вниз.

Сила тяжести сообщает телам, находящимся около поверхности Земли ускорение, которое называют ускорением свободного падения, обозначают его как $overline{g}$. По второму закону Ньютона имеем:

[overline{g}=frac{{overline{F}}_t}{m}left(6right).]

Учитывая выражение (5), имеем:

[left|overline{g}right|=gamma frac{M}{{left(R+hright)}^2}left(7right).]

Непосредственно на поверхности Земли (при $h=0$) величина ускорения свободного падения равна:

[g=gamma frac{M}{R^2}left(8right),]

величина ускорения свободного падения, вычисленная из (8) приблизительно равна $gapprox 9,8 frac{м}{с^2}.$ Следует знать, что даже у поверхности Земли модуль ускорения свободного падения не везде одинаков, так как Земля не является идеальным шаром, и она вращается вокруг своей оси и движется по криволинейной траектории вокруг Солнца.

Используя второй закон Ньютона и выражение (8) силу тяжести записывают как:

[{overline{F}}_t=moverline{g}left(9right).]

Примеры задач с решением

Читать дальше: закон Паскаля для жидкостей и газов.

Всемирное тяготение

6 Закон всемирного тяготения

1. В
   природе исключительную роль играют
   силы тяготения.
   Закон, которому они подчиняются, — закон
   всемирного тяготения – открыт Ньютоном
   в 1687 году.

Согласно
этому закону любые
две материальные точки притягиваются
друг к другу с силой, прямо пропорциональной
произведению масс этих точек, обратно
пропорциональной квадрату расстояния
между ними и направленной по прямой,
соединяющей эти точки
(рис.13).

Численное значение
силы тяготения

(6.1)

здесь:
m₁
и m₂
— массы
материальных точек; r
— расстояние между точками; 
— гравитационная
постоянная (размерный коэффициент
пропорциональности, зависящий от выбора
единиц измерения,
F,
m
и r)

1. Чтобы
   придать закону тяготения векторный
   вид, проведём от первой точки ко второй
   радиус-вектор
   и умножим правую

часть
(6.1) на единичный вектор этого направления

.
Тогда сила, действующая на второе тело
со стороны первого,
будет равна:

Знак
“минус” означает, что направления
радиус-вектора
и силыпротивоположны.

1. Силы
   тяготения подчиняются третьему закону
   Ньютона: они равны по величине и
   противоположны по направлению:

1. Силы
   тяготения – всепроникающие
   силы: от них
   нельзя экранироваться, их нельзя усилить
   или ослабить. Материальная среда, в
   которой находятся взаимодействующие
   тела, на величину и направление силы
   тяготения никакого влияния не оказывает.

2. Формула
   (6.1) позволяет найти силу гравитационного
   взаимодействия между материальными
   точками.

Чтобы
рассчитать силу тяготения между телами,
размеры которых соизмеримы с расстояниями
между ними, поступают следующим образом.
Оба тела разбивают на столь малые
элементы, что каждый такой элемент можно
считать материальной точкой. Выбирают
в первом теле произвольный элемент и
определяют результирующую
силу, действующую на него со стороны
всех
элементов второго тела, иначе говоря,
определяют силу,
с которой второе тело в целом притягивает
к себе этот выделенный элемент.
Затем проделывают то же самое для
остальных элементов первого тела, после
чего находят полную геометрическую
сумму сил, найденная сумма и будет
представлять собой силу, с которой
второе тело действует на первое. С такой
же по величине, но противоположной по
направлению силой первое тело действует
на второе. Расчёт показывает, что
математическое выражение для силы
тяготения, действующей между однородными
шарами,
шарами с плотностью, зависящей от r
(r
– расстояние
от центра шара), между сферическими
слоями будет совпадать с (6.1), если под
r
понимать расстояние между центрами
этих тел (рис.14). Закон тяготения справедлив
также для тел, одно из которых — однородный
шар, а другое — материальная точка (с
этим случаем мы
имеем дело,
например, при расчёте силы, с которой
Земля притягивает к себе находящиеся
на её поверхности тела).

1. В
   формулу закона тяготения входит масса.
   Масса уже фигурировала в уравнениях
   механики, в частности, в выражении
   второго закона Ньютона. Там она
   характеризовала инерционные
   свойства
   тел и называлась “инертной”.

Роль
массы в законе тяготения иная.
Здесь она определяет силу гравитационного
взаимодействия материальных тел, т.е.
является ме-

рой
их гравитационных свойств. Эту массу,
в отличие от “инертной”, называют
“гравитационной”
или “тяжёлой”.

Различать
гравитационную и инертную массу в
настоящее время нет необходимости.
Многими, весьма тонкими экспериментами
(Бессель, Этвеш, Крылов и др.) установлено,
что инертная и гравитационная массы с
точностью до 10^-8
совпадают. Это, в сущности, одна и та же
физическая величина, по-разному
проявляющая себя в различных физических
явлениях. С одной стороны, масса — это
мера инерционных
свойств, с другой — мера гравитационных
свойств.

1. Гравитационная
   постоянная 
   является универсальной константой, не
   зависящей от природы взаимодействующих
   тел. Эта величина

численно
равна силе,
с которой притягиваются друг к другу
две материальные точки единичной
массы,
расположенные на
единичном
расстоянии друг от друга: если |
m₁
|=
| m₂
|
= 1, | r
|
= 1, то | 
|
= | F
|.

Численное
значение 
было впервые определено У. Кавендишем

в
1797 г.

Это
значит, что два точечных тела (или шара)
массой по 1кг каждый, расположенные на
расстоянии 1м друг от друга, притягиваются
с силой 6,6710^-11
Н.

Необычайно
малая величина 

указывает на то, что гравитационное
взаимодействие становится заметным
только в случае очень больших
масс.
В механике таких объектов, как атомы и
молекулы, гравитационные силы практически
не играют никакой роли.

Движение
же таких макроскопических тел, как
звёзды, Солнце, планеты, Луна, спутники
(после того, как выключены двигатели)
полностью управляется силами тяготения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Закон всемирного тяготения

Закон всемирного тяготения

Можно лишь догадываться о волнении, охватившем Ньютона, когда он пришел к великому результату: одна и та же причина вызывает явления поразительно широкого диапазона — от падения брошенного камня на Землю до движения огромных космических тел. Ньютон нашел эту причину и смог точно выразить ее в виде одной формулы — закона всемирного тяготения.

Так как сила всемирного тяготения сообщает всем телам одно и то же ускорение независимо от их массы, то она должна быть пропорциональна массе того тела, на которое действует:

Определение закона всемирного тяготения

Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними:

Коэффициент пропорциональности G называется гравитационной постоянной.

Гравитационная постоянная численно равна силе притяжения между двумя материальными точками массой 1 кг каждая, если расстояние между ними равно 1 м. Ведь при m₁=m₂=1 кг и R=1 м получаем G=F (численно).

Нужно иметь в виду, что закон всемирного тяготения (4.5) как всеобщий закон справедлив для материальных точек. При этом силы гравитационного взаимодействия направлены вдоль линии, соединяющей эти точки (рис.4.2). Подобного рода силы называются центральными.

Определение гравитационной постоянной

Теперь выясним, как можно найти гравитационную постоянную. Прежде всего заметим, что G имеет определенное наименование. Это обусловлено тем, что единицы (и соответственно наименования) всех величин, входящих в закон всемирного тяготения, уже были установлены ранее. Закон же тяготения дает новую связь между известными величинами с определенными наименованиями единиц. Именно поэтому коэффициент оказывается именованной величиной. Пользуясь формулой закона всемирного тяготения, легко найти наименование единицы гравитационной постоянной в СИ:

Н•м2/кг2=м3/(кг•с2).

Для количественного определения G нужно независимо определить все величины, входящие в закон всемирного тяготения: обе массы, силу и расстояние между телами. Использовать для этого астрономические наблюдения нельзя, так как определить массы планет, Солнца, да и Земли, можно лишь на основе самого закона всемирного тяготения, если значение гравитационной постоянной известно. Опыт должен быть проведен на Земле с телами, массы которых можно измерить на весах.

Трудность состоит в том, что гравитационные силы между телами небольших масс крайне малы. Именно по этой причине мы не замечаем притяжение нашего тела к окружающим предметам и взаимное притяжение предметов друг к другу, хотя гравитационные силы — самые универсальные из всех сил в природе. Два человека массами по 60 кг на расстоянии 1 м друг от друга притягиваются с силой всего лишь порядка 10^-9 Н. Поэтому для измерения гравитационной постоянной нужны достаточно тонкие опыты.

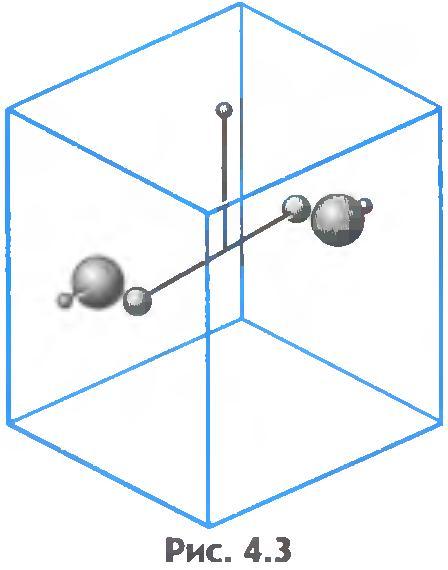
Впервые гравитационная постоянная была измерена английским физиком Г. Кавендишем в 1798 г. с помощью прибора, называемого крутильными весами. Схема крутильных весов показана на рисунке 4.3. На тонкой упругой нити подвешено легкое коромысло с двумя одинаковыми грузиками на концах. Рядом неподвижно закреплены два тяжелых шара. Между грузиками и неподвижными шарами действуют силы тяготения. Под влиянием этих сил коромысло поворачивается и закручивает нить. По углу закручивания можно определить силу притяжения. Для этого нужно только знать упругие свойства нити. Массы тел известны, а расстояние между центрами взаимодействующих тел можно непосредственно измерить.

Из этих опытов было получено следующее значение для гравитационной постоянной:

Зависимость ускорения свободного падения тел от географической широты

Одна из причин увеличения ускорения свободного падения при перемещении точки, где находится тело, от экватора к полюсам, состоит в том, что земной шар несколько сплюснут у полюсов и расстояние от центра Земли до ее поверхности у полюсов меньше, чем на экваторе. Другой, более существенной причиной является вращение Земли.

Равенство инертной и гравитационной масс

Самым поразительным свойством гравитационных сил является то, что они сообщают всем телам, независимо от их масс, одно и то же ускорение. Что бы вы сказали о футболисте, удар которого одинаково ускорял бы обыкновенный кожаный мяч и двухпудовую гирю? Каждый скажет, что это невозможно. А вот Земля является именно таким «необыкновенным футболистом» с той только разницей, что действие ее на тела не носит характера кратковременного удара, а продолжается непрерывно миллиарды лет.

Необыкновенное свойство гравитационных сил, как мы уже говорили, объясняется тем, что эти силы пропорциональны массам обоих взаимодействующих тел. Факт этот не может не вызывать удивления, если над ним хорошенько задуматься. Ведь масса тела, которая входит во второй закон Ньютона, определяет инертные свойства тела, т. е. его способность приобретать определенное ускорение под действием данной силы. Эту массу естественно назвать инертной массой и обозначить через m_и.

Казалось бы, какое отношение она может иметь к способности тел притягивать друг друга? Массу, определяющую способность тел притягиваться друг к другу, следует назвать гравитационной массой m_г.

Из механики Ньютона совсем не следует, что инертная и гравитационная массы одинаковы, т. е. что

Равенство (4.6) является непосредственным следствием из опыта. Оно означает, что можно говорить просто о массе тела как о количественной мере как инертных, так и гравитационных его свойств.

Значение закона всемирного тяготения

Но если подойти к этой теме, более кардинально, то выясняется, что закон всемирного тяготения не везде есть возможность его применения. Этот закон нашел свое применение для тел, которые имеют форму шара, его можно использовать для материальных точек, а также он приемлем для шара, имеющего большой радиус, где этот шар может взаимодействовать с телами, гораздо меньшими, чем его размеры.

Но вот для тела и бесконечной плоскости, а также для взаимодействия бесконечного стержня и шара эту формулу применять нельзя.

Как вы уже догадались из информации, предоставленной на этом уроке, что закон всемирного тяготения является основой в изучении небесной механики. А как вы знаете, небесная механика изучает движение планет.

Благодаря этому закону всемирного тяготения, появилась возможность в более точном определении расположения небесных тел и возможность вычисления их траектории.

С помощью этого закона можно рассчитать и движение искусственных спутников Земли, а также и созданных других межпланетных аппаратов.

Но вот для тела и бесконечной плоскости, а также для взаимодействия бесконечного стержня и шара эту формулу применять нельзя.

С помощью этого закона Ньютон смог объяснить не только то, как движутся планеты, но и почему возникают морские приливы и отливы. По истечении времени, благодаря трудам Ньютона, астрономам удалось открыть такие планеты Солнечной системы, как Нептун и Плутон.

Важность открытия закона всемирного тяготения заключается в том, что с его помощью появилась возможность делать прогнозы солнечных и лунных затмений и с точностью рассчитывать движения космических кораблей.

Силы всемирного тяготения являются наиболее универсальными со всех сил природы. Ведь их действие распространяется на взаимодействие между любыми телами, имеющими массу. А как известно, то любое тело обладает массой. Силы тяготения действуют сквозь любые тела, так как для сил тяготения нет приград.

Задача

А теперь, чтобы закрепить знания о законе всемирного тяготения, давайте попробуем рассмотреть и решить интересную задачу.
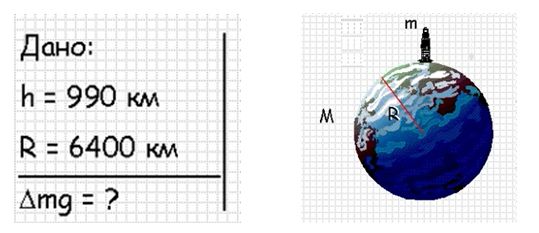
Ракета поднялась на высоту h равную 990 км. Определите, насколько уменьшилась сила тяжести, действующая на ракету на высоте h, по сравнению с силой тяжести mg, действующей на нее у поверхности Земли?
Радиус Земли R = 6400 км. Обозначим через m массу ракеты, а через M массу Земли.

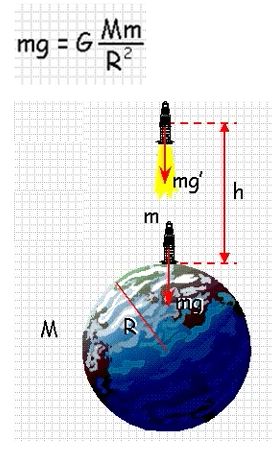
Будем считать, что на ракету действует только сила тяготения Земли и центробежной силой можно пренебречь из-за малой угловой скорости вращения Земли. Поэтому можно записать, что сила тяжести на Земле:

На высоте h сила тяжести равняется:

Отсюда вычислим:

Подстановка значение даст результат:

Интересные факты

Легенду про то, как Ньютон открыл закон всемирного тяготения, получив яблоком по макушке, придумал Вольтер. Причем сам Вольтер уверял, что эту правдивую историю ему рассказала любимая племянница Ньютона Кэтрин Бартон. Вот только странно, что ни сама племянница, ни ее очень близкий друг Джонатан Свифт, в своих воспоминаниях о Ньютоне про судьбоносное яблоко никогда не упоминали. Кстати и сам Исаак Ньютон, подробно записывая в своих тетрадях результаты экспериментов по поведению разных тел, отмечал только сосуды, наполненные золотом, серебром, свинцом, песком, стеклом водой или пшеницей, ни как ни о яблоке. Впрочем, это не помешало потомкам Ньютона водить экскурсантов по саду в имении Вулсток и показывать им ту самую яблоню, пока ее не сломала буря.

Да, яблоня была, и яблоками наверняка с нее падали, но насколько велика заслуга яблока в деле открытия закона всемирного тяготения?

Споры о яблоке не затихают вот уже 300 лет, так же как и споры о самом законе всемирного тяготения верее о том, кому принадлежит приоритет открытия.ук

Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: